Derivada parcial

ImprimirCitar

Derivativo de una función con múltiples variables

En matemáticas, una derivada parcial de una función de varias variables es su derivada con respecto a una de esas variables, manteniendo constantes las demás (a diferencia de la derivada total, en la que todas las variables se permite variar). Las derivadas parciales se utilizan en cálculo vectorial y geometría diferencial.

El derivado parcial de una función ${displaystyle f(x,y,dots)}$ con respecto a la variable $x$ es denotado por

f_{x}

{displaystyle f'_{x}}

{displaystyle partial _{x}f}

{displaystyle D_{x}f}

{displaystyle D_{1}f}

{displaystyle {frac {partial }{partial x}}f}

, o

frac{partial f}{partial x}

Se puede considerar como la tasa de cambio de la función en la $x$ - dirección.

A veces, para ${displaystyle z=f(x,y,ldots)}$ , el derivado parcial de $z$ con respecto a $x$ es denotado como ${displaystyle {tfrac {partial z}{partial x}}.}$ Dado que un derivado parcial generalmente tiene los mismos argumentos que la función original, su dependencia funcional a veces se indica explícitamente por la notación, como en:

{displaystyle f'_{x}(x,y,ldots),{frac {partial f}{partial x}}(x,y,ldots).}

El símbolo que se usa para denotar derivadas parciales es ∂. Uno de los primeros usos conocidos de este símbolo en matemáticas es del Marqués de Condorcet de 1770, quien lo usó para diferencias parciales. La notación moderna de derivadas parciales fue creada por Adrien-Marie Legendre (1786), aunque luego la abandonó; Carl Gustav Jacob Jacobi reintrodujo el símbolo en 1841.

Definición

Como los derivados ordinarios, el derivado parcial se define como un límite. Vamos U ser un subconjunto abierto $mathbb {R} ^{n}$ y ${displaystyle f:Uto mathbb {R} }$ una función. El derivado parcial de f en el punto ${displaystyle mathbf {a} =(a_{1},ldotsa_{n})in U}$ con respecto a i- la variable x_i se define como

{displaystyle {begin{aligned}{frac {partial }{partial x_{i}}}f(mathbf {a})&=lim _{hto 0}{frac {f(a_{1},ldotsa_{i-1},a_{i}+h,a_{i+1},ldotsa_{n})-f(a_{1},ldotsa_{i},dotsa_{n})}{h}}\&=lim _{hto 0}{frac {f(mathbf {a} +hmathbf {e_{i}})-f(mathbf {a})}{h}}end{aligned}}}

Incluso si todos los derivados parciales ∂f/∂x_i()a) existen en un punto dado a, la función no necesita ser continua allí. Sin embargo, si todos los derivados parciales existen en un barrio de a y son continuos allí, entonces f es totalmente diferente en ese vecindario y el derivado total es continuo. En este caso, se dice que f es un C¹ función. Esto se puede utilizar para generalizar las funciones de valor vectorial, ${displaystyle f:Uto mathbb {R} ^{m}}$ , usando cuidadosamente un argumento basado en componentes.

El derivado parcial $frac{partial f}{partial x}$ se puede ver como otra función definida en U y puede ser parcialmente diferenciado. Si todos los derivados parciales de segundo orden mixtos son continuos en un punto (o en un conjunto), f se denomina a C² función en ese punto (o en ese conjunto); en este caso, los derivados parciales pueden ser intercambiados por el teorema de Clairaut:

{displaystyle {frac {partial ^{2}f}{partial x_{i}partial x_{j}}}={frac {partial ^{2}f}{partial x_{j}partial x_{i}}}.}

Notation

Para los siguientes ejemplos, $f$ ser una función en $x,y$ y $z$ .

Derivadas parciales de primer orden:

{displaystyle {frac {partial f}{partial x}}=f'_{x}=partial _{x}f.}

Derivadas parciales de segundo orden:

{displaystyle {frac {partial ^{2}f}{partial x^{2}}}=f''_{xx}=partial _{xx}f=partial _{x}^{2}f.}

Derivadas mixtas de segundo orden:

{displaystyle {frac {partial ^{2}f}{partial y,partial x}}={frac {partial }{partial y}}left({frac {partial f}{partial x}}right)=(f'_{x})'_{y}=f''_{xy}=partial _{yx}f=partial _{y}partial _{x}f.}

Derivadas mixtas y parciales de orden superior:

{displaystyle {frac {partial ^{i+j+k}f}{partial x^{i}partial y^{j}partial z^{k}}}=f^{(i,j,k)}=partial _{x}^{i}partial _{y}^{j}partial _{z}^{k}f.}

Cuando se trata de funciones de múltiples variables, algunas de estas variables pueden estar relacionadas entre sí, por lo tanto puede ser necesario especificar explícitamente qué variables se mantienen constantes para evitar la ambigüedad. En campos como la mecánica estadística, el derivado parcial de $f$ con respecto a $x$ , tenso $y$ y $z$ constante, se expresa a menudo como

{displaystyle left({frac {partial f}{partial x}}right)_{y,z}.}

Convencionalmente, para mayor claridad y simplicidad de la notación, la derivada parcial función y el valor de la función en un punto específico se fusionan al incluir los argumentos de la función cuando el parcial se utiliza el símbolo de derivada (notación de Leibniz). Así, una expresión como

{frac {partial f(x,y,z)}{partial x}}

se utiliza para la función, mientras que

{displaystyle {frac {partial f(u,v,w)}{partial u}}}

se puede utilizar para el valor de la función en el punto ${displaystyle (x,y,z)=(u,v,w)}$ . Sin embargo, esta convención se rompe cuando queremos evaluar el derivado parcial en un punto como ${displaystyle (x,y,z)=(17,u+v,v^{2})}$ . En tal caso, la evaluación de la función debe expresarse de manera inmutable como

{displaystyle {frac {partial f(x,y,z)}{partial x}}(17,u+v,v^{2})}

{displaystyle left.{frac {partial f(x,y,z)}{partial x}}right|_{(x,y,z)=(17,u+v,v^{2})}}

para utilizar la notación de Leibniz. Así, en estos casos, puede ser preferible utilizar la notación diferencial del operador Euler con $D_{i}$ como el símbolo derivado parcial con respecto al ila variable. Por ejemplo, uno escribiría ${displaystyle D_{1}f(17,u+v,v^{2})}$ por el ejemplo descrito anteriormente, mientras que la expresión ${displaystyle D_{1}f}$ representa el derivado parcial función con respecto a la primera variable.

Para los derivados parciales de orden superior, el derivado parcial (función) de ${displaystyle D_{i}f}$ con respecto a jla variable se denota ${displaystyle D_{j}(D_{i}f)=D_{i,j}f}$ . Eso es, ${displaystyle D_{j}circ D_{i}=D_{i,j}}$ , de modo que las variables se enumeran en el orden en que se toman los derivados, y por lo tanto, en orden inverso de cómo la composición de los operadores se notifica generalmente. Por supuesto, el teorema de Clairaut implica que ${displaystyle D_{i,j}=D_{j,i}}$ siempre y cuando las condiciones de regularidad comparativamente leves f están satisfechos.

Gradiente

Un ejemplo importante de una función de varias variables es el caso de una función de valor escalar f()x₁,... x_n) en un dominio en el espacio Euclideano $mathbb {R} ^{n}$ (por ejemplo, en adelante $R^2$ o $mathbb{R} ^{3}$ ). En este caso f tiene un derivado parcial ∂f/∂x_j con respecto a cada variable x_j. En el punto a, estos derivados parciales definen el vector

nabla f(a)=left({frac {partial f}{partial x_{1}}}(a),ldots{frac {partial f}{partial x_{n}}}(a)right).

Este vector se llama el gradiente de f en a. Si f es diferenciable en cada punto de algún dominio, entonces el gradiente es una función vectorial ∇f que lleva el punto a a la vector ∇f(a). En consecuencia, el gradiente produce un campo vectorial.

Un abuso común de la notación es definir el operador del operador (llamadas) como sigue en el espacio Euclideano tridimensional $mathbb{R} ^{3}$ con vectores de unidad ${hat {{mathbf {i}}}},{hat {{mathbf {j}}}},{hat {{mathbf {k}}}}$ :

{displaystyle nabla =left[{frac {partial }{partial x}}right]{hat {mathbf {i} }}+left[{frac {partial }{partial y}}right]{hat {mathbf {j} }}+left[{frac {partial }{partial z}}right]{hat {mathbf {k} }}}

O, más generalmente, para n-dimensional Espacio euclidiano $mathbb {R} ^{n}$ con coordenadas $x_{1},ldotsx_{n}$ y vectores de unidad ${displaystyle {hat {mathbf {e} }}_{1},ldots{hat {mathbf {e} }}_{n}}$ :

{displaystyle nabla =sum _{j=1}^{n}left[{frac {partial }{partial x_{j}}}right]{hat {mathbf {e} }}_{j}=left[{frac {partial }{partial x_{1}}}right]{hat {mathbf {e} }}_{1}+left[{frac {partial }{partial x_{2}}}right]{hat {mathbf {e} }}_{2}+dots +left[{frac {partial }{partial x_{n}}}right]{hat {mathbf {e} }}_{n}}

Derivada direccional

(feminine)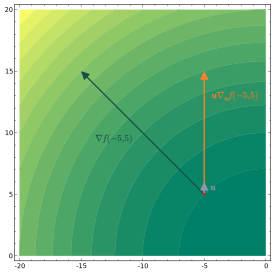

Una parcela de contorno

f(x, y)=x^2 + y^2

, mostrando el vector gradiente en negro, y el vector de unidad

mathbf {u}

escalada por el derivado direccional en la dirección

mathbf {u}

en naranja. El vector gradiente es más largo porque los puntos gradientes en la dirección de mayor tasa de aumento de una función.

El derivado direccional de una función de escalar

{displaystyle f(mathbf {x})=f(x_{1},x_{2},ldotsx_{n})}

un vector

{displaystyle mathbf {v} =(v_{1},ldotsv_{n})}

es la función

{displaystyle nabla _{mathbf {v} }{f}}

definido por el límite

{displaystyle nabla _{mathbf {v} }{f}(mathbf {x})=lim _{hto 0}{frac {f(mathbf {x} +hmathbf {v})-f(mathbf {x})}{h}}.}

Esta definición es válida en una amplia gama de contextos, por ejemplo donde la norma de un vector (y por lo tanto un vector unitario) no está definida.

Ejemplo

Suponga que f es una función de más de una variable. Por ejemplo,

{displaystyle z=f(x,y)=x^{2}+xy+y^{2}}

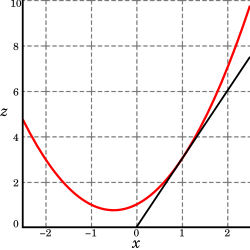
Un gráfico de z = x² + xy + Sí.². Para el derivado parcial en (1, 1) que sale Sí. constante, la línea tangente correspondiente es paralela a la xz- Avión.

Una rebanada del gráfico anterior que muestra la función en la xz- Avión Sí. = 1. Tenga en cuenta que los dos ejes se muestran aquí con diferentes escalas. La pendiente de la línea tangente es 3.

El gráfico de esta función define una superficie en el espacio euclidiano. A cada punto de esta superficie, hay un número infinito de líneas tangentes. La diferenciación parcial es el acto de elegir una de estas líneas y encontrar su pendiente. Por lo general, las líneas de mayor interés son aquellas que son paralelas a las $xz$ -plano, y los que son paralelos al $yz$ -plano (que resulta de la celebración de cualquiera $y$ o $x$ constante, respectivamente).

Para encontrar la pendiente de la línea tangente a la función en ${displaystyle P(1,1)}$ y paralelo al $xz$ -plano, tratamos $y$ como una constante. El gráfico y este avión se muestran a la derecha. A continuación, vemos cómo se ve la función en el plano $y=1$ . Al encontrar el derivado de la ecuación asumiendo que $y$ es una constante, encontramos que la pendiente de $f$ en el punto $(x,y)$ es:

{displaystyle {frac {partial z}{partial x}}=2x+y.}

Así que... $(1,1)$ , por sustitución, la pendiente es 3. Por lo tanto,

frac{partial z}{partial x} = 3

en el punto $(1,1)$ . Es decir, el derivado parcial de $z$ con respecto a $x$ a $(1,1)$ es 3, como se muestra en el gráfico.

La función f se puede reinterpretar como una familia de funciones de una variable indexada por las otras variables:

{displaystyle f(x,y)=f_{y}(x)=x^{2}+xy+y^{2}.}

En otras palabras, cada valor de y define una función, denominada f_y, que es una función de una variable x. Eso es,

{displaystyle f_{y}(x)=x^{2}+xy+y^{2}.}

En esta sección, la notación de subíndices f_y denota una función que depende de un valor fijo de y, y no una derivada parcial.

Una vez un valor Sí. es elegido, digamos a, entonces f()x,Sí.) determina una función f_a que traza una curva x² + ax + a² sobre $xz$ -plane:

{displaystyle f_{a}(x)=x^{2}+ax+a^{2}.}

En esta expresión, a es una constante, no una variable, por lo que f_a es una función de una sola variable real, que es x. En consecuencia, se aplica la definición de la derivada para una función de una variable:

{displaystyle f_{a}'(x)=2x+a.}

El procedimiento anterior se puede realizar para cualquier elección de a. Reunir las derivadas en una función da una función que describe la variación de f en la dirección x:

{displaystyle {frac {partial f}{partial x}}(x,y)=2x+y.}

Esta es la derivada parcial de f con respecto a x. Aquí ∂ es una d redondeada llamada símbolo de derivada parcial; para distinguirla de la letra d, ∂ a veces se pronuncia "parcial".

Derivadas parciales de orden superior

Los derivados parciales de orden secundario y superior se definen analógicamente a los derivados de orden superior de las funciones univariadas. Para la función $f(x, y,...)$ el segundo derivado parcial con respecto a x es simplemente el derivado parcial del derivado parcial (ambos respecto a x):

{displaystyle {frac {partial ^{2}f}{partial x^{2}}}equiv partial {frac {partial f/partial x}{partial x}}equiv {frac {partial f_{x}}{partial x}}equiv f_{xx}.}

La derivada parcial cruzada con respecto a x e y se obtiene tomando la derivada parcial de f con respecto a x , y luego tomando la derivada parcial del resultado con respecto a y, para obtener

{displaystyle {frac {partial ^{2}f}{partial y,partial x}}equiv partial {frac {partial f/partial x}{partial y}}equiv {frac {partial f_{x}}{partial y}}equiv f_{xy}.}

El teorema de Schwarz establece que si las segundas derivadas son continuas, la expresión de la derivada parcial cruzada no se ve afectada por qué variable se toma la derivada parcial con respecto a la primera y cuál se toma en segundo lugar. Eso es,

{displaystyle {frac {partial ^{2}f}{partial x,partial y}}={frac {partial ^{2}f}{partial y,partial x}}}

o equivalente ${displaystyle f_{yx}=f_{xy}.}$

Las derivadas parciales propias y cruzadas aparecen en la matriz hessiana que se utiliza en las condiciones de segundo orden en los problemas de optimización. Las derivadas parciales de orden superior se pueden obtener por diferenciación sucesiva

Análogo de la antiderivada

Existe un concepto para derivadas parciales que es análogo a las antiderivadas para derivadas regulares. Dada una derivada parcial, permite la recuperación parcial de la función original.

Considere el ejemplo de

{displaystyle {frac {partial z}{partial x}}=2x+y.}

El "parcial" La integral se puede tomar con respecto a x (tratando a y como constante, de manera similar a la diferenciación parcial):

{displaystyle z=int {frac {partial z}{partial x}},dx=x^{2}+xy+g(y).}

Aquí, el "constante" de la integración ya no es una constante, sino una función de todas las variables de la función original excepto x. La razón de esto es que todas las otras variables se tratan como constantes al tomar el derivado parcial, por lo que cualquier función que no implica $x$ desaparecerá cuando tome el derivado parcial, y tenemos que tener en cuenta esto cuando tomemos el antiderivativo. La forma más general de representar esto es que el "constante" represente una función desconocida de todas las otras variables.

Así, el conjunto de funciones $x^2 + xy + g(y)$ , donde g es cualquier función de un solo compromiso, representa todo el conjunto de funciones en variables x,Sí. que podría haber producido x- derivado parcial $2x + y$ .

Si se conocen todas las derivadas parciales de una función (por ejemplo, con el gradiente), las antiderivadas se pueden emparejar mediante el proceso anterior para reconstruir la función original hasta una constante. Sin embargo, a diferencia del caso de una sola variable, no todos los conjuntos de funciones pueden ser el conjunto de todas las (primeras) derivadas parciales de una sola función. En otras palabras, no todos los campos vectoriales son conservativos.

Aplicaciones

Geometría

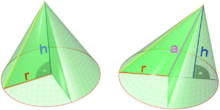
El volumen de un cono depende de la altura y el radio

El volumen V de un cono depende de la altura del cono h y de su radio r según la fórmula

V(r, h) = frac{pi r^2 h}{3}.

La derivada parcial de V con respecto a r es

frac{ partial V}{partial r} = frac{ 2 pi r h}{3},

que representa la tasa con la que el volumen de un cono cambia si su radio es variado y su altura se mantiene constante. El derivado parcial con respecto a $h$ iguales ${displaystyle {frac {pi r^{2}}{3}},}$ que representa la tasa con la que el volumen cambia si su altura es variada y su radio se mantiene constante.

Por el contrario, la derivada total de V con respecto a r y h son respectivamente

{displaystyle {frac {dV}{dr}}=overbrace {frac {2pi rh}{3}} ^{frac {partial V}{partial r}}+overbrace {frac {pi r^{2}}{3}} ^{frac {partial V}{partial h}}{frac {dh}{dr}}}

{displaystyle {frac {dV}{dh}}=overbrace {frac {pi r^{2}}{3}} ^{frac {partial V}{partial h}}+overbrace {frac {2pi rh}{3}} ^{frac {partial V}{partial r}}{frac {dr}{dh}}}

La diferencia entre la derivada total y parcial es la eliminación de dependencias indirectas entre variables en derivadas parciales.

Si (por alguna razón arbitraria) las proporciones del cono tienen que permanecer iguales, y la altura y el radio están en una proporción fija k,

{displaystyle k={frac {h}{r}}={frac {dh}{dr}}.}

Esto da la derivada total con respecto a r:

{displaystyle {frac {dV}{dr}}={frac {2pi rh}{3}}+{frac {pi r^{2}}{3}}k}

que se simplifica a:

{displaystyle {frac {dV}{dr}}=kpi r^{2}}

Del mismo modo, la derivada total con respecto a h es:

{displaystyle {frac {dV}{dh}}=pi r^{2}}

La derivada total con respecto a tanto r como a h del volumen previsto como función escalar de estas dos variables viene dada por el vector gradiente

{displaystyle nabla V=left({frac {partial V}{partial r}},{frac {partial V}{partial h}}right)=left({frac {2}{3}}pi rh,{frac {1}{3}}pi r^{2}right).}

Optimización

Las derivadas parciales aparecen en cualquier problema de optimización basado en cálculo con más de una variable de elección. Por ejemplo, en economía, una empresa puede desear maximizar el beneficio π(x, y) con respecto a la elección de las cantidades x y y de dos tipos diferentes de salida. Las condiciones de primer orden para esta optimización son π_x = 0 = π_y. Dado que ambas derivadas parciales π_x y π_y generalmente serán funciones de ambos argumentos x y y, estas dos condiciones de primer orden forman un sistema de dos ecuaciones con dos incógnitas.

Termodinámica, mecánica cuántica y física matemática

Las derivadas parciales aparecen en ecuaciones termodinámicas como la ecuación de Gibbs-Duhem, en mecánica cuántica como la ecuación de onda de Schrödinger y en otras ecuaciones de la física matemática. Aquí, las variables que se mantienen constantes en derivadas parciales pueden ser una relación de variables simples como fracciones molares x_i en el siguiente ejemplo que involucra las energías de Gibbs en un sistema de mezcla ternario:

{displaystyle {bar {G_{2}}}=G+(1-x_{2})left({frac {partial G}{partial x_{2}}}right)_{frac {x_{1}}{x_{3}}}}

Expresar fracciones molares de un componente como funciones de otros componentes ' fracción molar y relaciones molares binarias:

{displaystyle x_{1}={frac {1-x_{2}}{1+{frac {x_{3}}{x_{1}}}}}}

{displaystyle x_{3}={frac {1-x_{2}}{1+{frac {x_{1}}{x_{3}}}}}}

Los cocientes diferenciales se pueden formar en proporciones constantes como las anteriores:

{displaystyle left({frac {partial x_{1}}{partial x_{2}}}right)_{frac {x_{1}}{x_{3}}}=-{frac {x_{1}}{1-x_{2}}}}

{displaystyle left({frac {partial x_{3}}{partial x_{2}}}right)_{frac {x_{1}}{x_{3}}}=-{frac {x_{3}}{1-x_{2}}}}

Las proporciones X, Y, Z de las fracciones molares se pueden escribir para sistemas ternarios y multicomponentes:

{displaystyle X={frac {x_{3}}{x_{1}+x_{3}}}}

{displaystyle Y={frac {x_{3}}{x_{2}+x_{3}}}}

{displaystyle Z={frac {x_{2}}{x_{1}+x_{2}}}}

que se puede utilizar para resolver ecuaciones diferenciales parciales como:

{displaystyle left({frac {partial mu _{2}}{partial n_{1}}}right)_{n_{2},n_{3}}=left({frac {partial mu _{1}}{partial n_{2}}}right)_{n_{1},n_{3}}}

Esta igualdad se puede reorganizar para tener el cociente diferencial de las fracciones molares en un lado.

Cambio de tamaño de imagen

Las derivadas parciales son clave para los algoritmos de cambio de tamaño de imágenes que tienen en cuenta el objetivo. Ampliamente conocidos como tallado de costura, estos algoritmos requieren que a cada píxel de una imagen se le asigne una "energía" numérica. para describir su diferencia con los píxeles adyacentes ortogonales. Luego, el algoritmo elimina progresivamente filas o columnas con la energía más baja. La fórmula establecida para determinar la energía de un píxel (magnitud del gradiente en un píxel) depende en gran medida de las construcciones de derivadas parciales.

Economía

Las derivadas parciales desempeñan un papel destacado en la economía, en la que la mayoría de las funciones que describen el comportamiento económico postulan que el comportamiento depende de más de una variable. Por ejemplo, una función de consumo social puede describir la cantidad gastada en bienes de consumo en función tanto del ingreso como de la riqueza; la propensión marginal a consumir es entonces la derivada parcial de la función de consumo con respecto al ingreso.

Contenido relacionado

Más resultados...