Densidad de electrones

Densidad de electrones o densidad electrónica es la medida de la probabilidad de que un electrón esté presente en un elemento infinitesimal del espacio que rodea cualquier punto dado. Es una cantidad de escalar dependiendo de tres variables espaciales y normalmente se denota como *** *** ()r){displaystyle rho ({textbf {r})} o n()r){displaystyle n({textbf {r})}. La densidad se determina, por definición, por la normalización N{displaystyle N}- Función de onda electrónica que depende de 4N{displaystyle 4N} variables3N{textstyle 3N} espacial y N{displaystyle N} coordenadas de giro). Por el contrario, la densidad determina el modulo de función de onda hasta un factor de fase, proporcionando el fundamento formal de la teoría funcional de densidad.

Según la mecánica cuántica, debido al principio de incertidumbre a escala atómica no se puede predecir la ubicación exacta de un electrón, solo la probabilidad de que se encuentre en una posición dada; por lo tanto, los electrones en los átomos y las moléculas actúan como si estuvieran "borrados" en el espacio. Para los sistemas de un electrón, la densidad de electrones en cualquier punto es proporcional al cuadrado de la magnitud de la función de onda.

Definición

La densidad electrónica correspondiente a un normalizado N{displaystyle N}- Función de onda electrónica Ψ Ψ {displaystyle Psi } (con r{displaystyle {textbf}} y s{displaystyle s} denotar variables espaciales y de giro respectivamente) se define como

*** *** ()r)=.. Ψ Ψ Silencio*** *** ^ ^ ()r)SilencioΨ Ψ .. ,{displaystyle rho (mathbf {r})=langle Psi tención{hat {rho } {mathbf {r})

donde el operador correspondiente a la densidad observable es

*** *** ^ ^ ()r)=.. i=1Nδ δ ()r− − ri).{displaystyle {hat {rho }(mathbf {r})=sum _{i=1}^{N} delta (mathbf {r} -mathbf {r} _{i}}}}

Computing *** *** ()r){displaystyle rho (mathbf {r})} como se define arriba podemos simplificar la expresión como sigue.

*** *** ()r)=.. s1⋯ ⋯ .. sN∫ ∫ dr1⋯ ⋯ ∫ ∫ drN().. i=1Nδ δ ()r− − ri))SilencioΨ Ψ ()r1,s1,r2,s2,...,rN,sN)Silencio2=N.. s1⋯ ⋯ .. sN∫ ∫ dr2⋯ ⋯ ∫ ∫ drNSilencioΨ Ψ ()r,s1,r2,s2,...,rN,sN)Silencio2{displaystyle {begin{aligned}rho (mathbf {r}) ¿Qué? sum {{s}_{N}int mathrm {d} mathbf {r} _{1} cdots int mathrm {d} {r} _{N}mathbf {r} -mathbf {r} _{i})right) ¿Qué? _{N},s_{N} ¿Por qué? ################################################################################################################################################################################################################################################################ _{2} cdots int mathrm {d} {r} ¿Por qué? ¿Qué? - Hola.

En palabras: mantener un solo electrón todavía en posición r{displaystyle {textbf}} sumamos todos los arreglos posibles de los otros electrones. El factor N surge ya que todos los electrones son indistinguibles, y por lo tanto todas las integrales evalúan al mismo valor.

En las teorías funcionales de Hartree-Fock y densidad, la función de onda es típicamente representada como un único determinante de Slater construido a partir de N{displaystyle N} orbitales, φ φ k{displaystyle varphi _{k}, con ocupaciones correspondientes nk{displaystyle No.. En estas situaciones, la densidad simplifica

*** *** ()r)=.. k=1NnkSilencioφ φ k()r)Silencio2.{displaystyle rho (mathbf {r})=sum _{k=1}{N}n_{k} _{k}(mathbf {r}) WordPress^{2}

Propiedades generales

Por su definición, la densidad electrónica es una función no negativa que se integra al número total de electrones. Además, para un sistema con energía cinética T, la densidad satisface las desigualdades

12∫ ∫ dr()Silencio Silencio *** *** ()r))2≤ ≤ T.{displaystyle {frac {1}{2}}int mathrm {d} mathbf {r} {big (}nabla {sqrt {rho (mathbf {r}}}{big)}}} {2}leq} T.}

32()π π 2)4/3()∫ ∫ dr*** *** 3()r))1/3≤ ≤ T.{displaystyle {frac {3}{2}}left({frac {pi }{2}right)^{4/3}left(int mathrm {d} mathbf {r} rho ^{3}(mathbf {r})right)^{1/3}leq T.}

Para las energías cinéticas finitas, la primera (más fuerte) desigualdad coloca la raíz cuadrada de la densidad en el espacio Sobolev H1()R3){displaystyle ¿Qué?. Junto con la normalización y no negativa, esto define un espacio que contiene densidades físicamente aceptables como

JN={}*** *** Silencio*** *** ()r)≥ ≥ 0,*** *** 1/2()r)▪ ▪ H1()R3),∫ ∫ dr*** *** ()r)=N}.{fnMicrosoft Sans Serif} {f} {fn}fnMicrosoft Sans Serif} {nMicrosoft Sans Serif} {f}f} {f} {f}fnMicrosoft} {f}f} {f}f} {f}cH0}cH0}cH0}cH0}cH00}cH0}cH00}cH00cH00}cH00}cH00cH00}cH00}cH00cH00}cH00}cH00}cH00}cH00}cH00cH00}cH00}cH00}cH00}cH00}cH00cH00cH00}cH00}cH00}cH00cH00}cH00}cH00cH00}cH00}

La segunda desigualdad coloca la densidad en el espacio L3. Junto con la propiedad de normalización coloca densidades aceptables dentro de la intersección L¹ y L³– un superconjunto de JN{fnK} {fn} {fnK}}}.

Topología

Se conjetura que la densidad electrónica del estado fundamental de un átomo es una función monótonamente decreciente de la distancia desde el núcleo.

Condición de la cúspide nuclear

La densidad electrónica muestra cusps en cada núcleo en una molécula como resultado del potencial de Coulomb sin límites de electrones. Este comportamiento está cuantificado por la condición Kato cusp formulada en términos de densidad media esférica, *** *** ̄ ̄ {displaystyle {bar {rho }}, acerca de cualquier núcleo dado como

∂ ∂ ∂ ∂ rα α *** *** ̄ ̄ ()rα α )Silenciorα α =0=− − 2Zα α *** *** ̄ ̄ ()0).{displaystyle left.{frac {partial }{partial r_{alpha {fnh} {fnh} {fnhfnh}} {fnhfnh}}} {fn} {fnfn}}}} {fnfnfnfnfnfnfnfnf}}}} {fnfnf}}}}}}}}}} {f}}}}}}}}}}}}} {f}}}}}}} {f}}}}} {f}}}}}}}} {f}}} {ppppf}}}}}} {b}}}}}} {f}}} {f}} {b}}}}}}}}}}} {pppppppppppppppppppppb}}}}}}}} - Sí.

Es decir, el derivado radial de la densidad mediada esférica, evaluada en cualquier núcleo, es igual al doble de la densidad en ese núcleo multiplicado por el negativo del número atómico (Z{displaystyle Z}).

Comportamiento asintótico

La condición de cusp nuclear proporciona la casi nuclear (pequeña) r{displaystyle r}) comportamiento de densidad como

*** *** ()r)♪ ♪ e− − 2Zα α r.{displaystyle rho (r)sim e^{-2Z_{alpha }r},}

El largo alcance (grande r{displaystyle r}) comportamiento de la densidad es también conocido, tomando la forma

*** *** ()r)♪ ♪ e− − 22Ir.{displaystyle rho (r)sim e^{-2{sqrt {2mathrm {I} }r,.}

donde I es la energía de ionización del sistema.

Densidad de respuesta

Otra definición más general de una densidad es la "densidad de respuesta lineal". Esta es la densidad que cuando se contrae con cualquier operador de un electrón sin espín produce la propiedad asociada definida como la derivada de la energía. Por ejemplo, un momento dipolar es la derivada de la energía con respecto a un campo magnético externo y no es el valor esperado del operador sobre la función de onda. Para algunas teorías son iguales cuando la función de onda es convergente. Los números de ocupación no están limitados al rango de cero a dos, y por lo tanto a veces incluso la densidad de respuesta puede ser negativa en ciertas regiones del espacio.

Resumen

En las moléculas, las regiones de gran densidad de electrones generalmente se encuentran alrededor del átomo y sus enlaces. En sistemas deslocalizados o conjugados, como el fenol, el benceno y compuestos como la hemoglobina y la clorofila, la densidad electrónica es significativa en toda una región, es decir, en el benceno se encuentran por encima y por debajo del anillo plano. Esto a veces se muestra esquemáticamente como una serie de enlaces simples y dobles alternados. En el caso del fenol y el benceno, un círculo dentro de un hexágono muestra la naturaleza deslocalizada del compuesto. Esto se muestra a continuación:

En los compuestos con sistemas de anillos múltiples que están interconectados, esto ya no es exacto, por lo que se utilizan enlaces simples y dobles alternos. En compuestos como la clorofila y el fenol, algunos diagramas muestran una línea punteada o discontinua para representar la deslocalización de áreas donde la densidad de electrones es mayor junto a los enlaces simples. Los sistemas conjugados a veces pueden representar regiones donde la radiación electromagnética se absorbe en diferentes longitudes de onda, lo que da como resultado que los compuestos aparezcan coloreados. En los polímeros, estas áreas se conocen como cromóforos.

En cálculos químicos cuánticos, la densidad de electrones, ρ(r), es una función de las coordenadas r, definido como ρ(r)dr es el número de electrones en un pequeño volumen dr. Para las moléculas cerradas, *** *** ()r){displaystyle rho (mathbf {r})} se puede escribir en términos de una suma de productos de las funciones de base, φ:

*** *** ()r)=.. μ μ .. .. Pμ μ .. φ φ μ μ ()r)φ φ .. ()r){displaystyle rho (mathbf {r})=sum _{mu }sum _{nu }P_{munu }phi _{mu }(mathbf {r})phi _{nu }(mathbf {r})}

Densidad de electrones calculada para anilina, valores de alta densidad indican posiciones de átomo, valores de densidad intermedia enfatizan la unión, valores bajos proporcionan información sobre la forma y tamaño de una molécula.

donde P es la matriz de densidad. Las densidades de electrones a menudo se expresan en términos de una isosuperficie (una superficie de isodensidad) con el tamaño y la forma de la superficie determinados por el valor de la densidad elegida, o en términos de un porcentaje del total de electrones encerrados.

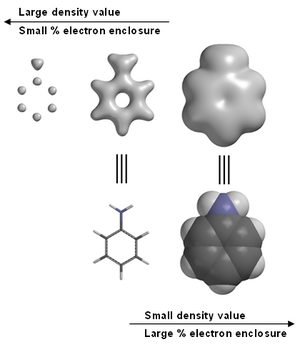
El software de modelado molecular suele proporcionar imágenes gráficas de la densidad electrónica. Por ejemplo, en anilina (ver imagen a la derecha). Los modelos gráficos, incluida la densidad de electrones, son una herramienta comúnmente empleada en la educación química. Nótese que en la imagen de la anilina situada más a la izquierda, las altas densidades de electrones están asociadas con los carbonos y el nitrógeno, pero los hidrógenos con un solo protón en sus núcleos no son visibles. Esta es la razón por la que la difracción de rayos X tiene dificultades para localizar posiciones de hidrógeno.

La mayoría de los paquetes de software de modelado molecular permiten al usuario elegir un valor para la densidad electrónica, a menudo denominado isovalor. Algunos programas también permiten la especificación de la densidad de electrones en términos de porcentaje del total de electrones encerrados. Según el isovalor (las unidades típicas son electrones por bohr cúbico) o el porcentaje del total de electrones encerrados, la superficie de densidad de electrones se puede usar para ubicar átomos, enfatizar densidades de electrones asociadas con enlaces químicos o para indicar el tamaño y la forma molecular general.

Gráficamente, la superficie de densidad de electrones también sirve como lienzo sobre el cual se pueden mostrar otras propiedades electrónicas. El mapa de potencial electrostático (la propiedad del potencial electrostático mapeado sobre la densidad electrónica) proporciona un indicador de la distribución de carga en una molécula. El mapa de potencial de ionización local (la propiedad del potencial de ionización local asignado a la densidad electrónica) proporciona un indicador de electrofilia. Y el mapa LUMO (orbital molecular desocupado más bajo asignado a la densidad electrónica) puede proporcionar un indicador de la nucleofilia.

Experimentos

Muchas técnicas experimentales pueden medir la densidad de electrones. Por ejemplo, la cristalografía cuántica a través del escaneo de difracción de rayos X, donde los rayos X de una longitud de onda adecuada se dirigen hacia una muestra y se realizan mediciones a lo largo del tiempo, brinda una representación probabilística de las ubicaciones de los electrones. A partir de estas posiciones, las estructuras moleculares, así como las distribuciones precisas de densidad de carga, a menudo se pueden determinar para sistemas cristalizados. La electrodinámica cuántica y algunas ramas de la teoría cuántica de campos también estudian y analizan la superposición de electrones y otros fenómenos relacionados, como el índice NCI, que permite el estudio de interacciones no covalentes utilizando la densidad de electrones. El análisis de población de Mulliken se basa en las densidades de electrones en las moléculas y es una forma de dividir la densidad entre los átomos para dar una estimación de las cargas atómicas.

En la microscopía electrónica de transmisión (TEM) y la dispersión inelástica profunda, así como en otros experimentos con partículas de alta energía, los electrones de alta energía interactúan con la nube de electrones para brindar una representación directa de la densidad electrónica. La TEM, la microscopía de túnel de barrido (STM) y la microscopía de fuerza atómica (AFM) se pueden utilizar para sondear la densidad electrónica de átomos individuales específicos.

Densidad de giro

Densidad de espín es la densidad electrónica aplicada a los radicales libres. Se define como la densidad electrónica total de los electrones de un espín menos la densidad electrónica total de los electrones del otro espín. Una de las formas de medirlo experimentalmente es mediante resonancia de espín de electrones, la difracción de neutrones permite el mapeo directo de la densidad de espín en el espacio 3D.