Demostraciones del pequeño teorema de Fermat

ImprimirCitar

Este artículo recopila una variedad de pruebas del pequeño teorema de Fermat, que establece que

{displaystyle a^{p}equiv a{pmod {p}}}

para todo número primo p y todo entero a (ver aritmética modular).

Simplificaciones

Algunas de las pruebas del pequeño teorema de Fermat que se dan a continuación dependen de dos simplificaciones.

El primero es que podemos asumir que $a$ está en el rango $0 \leq a \leq p - 1$ . Esta es una simple consecuencia de las leyes de aritmética modular; simplemente estamos diciendo que podemos reducir primero $a$ modulo $p$ . Esto es coherente con la reducción ${displaystyle a^{p}}$ modulo $p$ Como se puede comprobar.

En segundo lugar, basta con demostrar que

a^{{p-1}}equiv 1{pmod p}

para $a$ en el rango $1 \leq a \leq p - 1$ . De hecho, si la afirmación anterior se cumple para tal $a$ , multiplicando ambos lados por $a$ produce la forma original del teorema,

{displaystyle a^{p}equiv a{pmod {p}}}

Por otro lado, si $a = 0$ o $a = 1$ , el teorema se cumple trivialmente.

Pruebas combinatorias

Prueba contando collares

Esta es quizás la prueba conocida más simple, que requiere la menor cantidad de conocimientos matemáticos. Es un ejemplo atractivo de una prueba combinatoria (una prueba que implica contar una colección de objetos de dos maneras diferentes).

La prueba dada aquí es una adaptación de la prueba de Golomb.

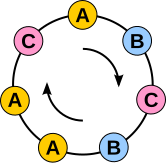
Para simplificar las cosas, supongamos que $a$ es un número entero positivo. Considere todas las posibles cadenas de símbolos $p$ , usando un alfabeto con $a$ diferentes símbolos. El número total de dichas cadenas es $a p$ , ya que hay $a$ posibilidades para cada una de las posiciones $p$ (ver regla de producto).

Por ejemplo, si $p = 5$ y $a = 2$ , entonces podemos usar un alfabeto con dos símbolos (por ejemplo, $A$ y $B$ ), y hay $25 = 32$ cadenas de longitud 5:

AAAAA

AAAAB

AAABA

ABBAA

AABAA

AABAB

AABBA

AAB

ABAAA

ABAAB

ABABA

ABA

ABBAA

ABBAB

ABBBA

ABB

BAAAA

BAAAB

BAABA

BAABB

BABAA

BABAB

BABBA

BAB

BBAAA

BBAAB

BBABA

BBA

BBBAA

BBBAB

BBBBA

BBB

A continuación argumentaremos que si eliminamos las cadenas que consisten en un solo símbolo de la lista (en nuestro ejemplo, $AAAAA$ y $BBBBB$ ), el resto $a p - a Las cadenas$ se pueden organizar en grupos, y cada grupo contiene exactamente cadenas $p$ . De ello se deduce que $a p - a$ es divisible por $p$ .

Collares

Collar que representa siete cuerdas diferentes (

ABCBAAC

BCBAACA

CBAACAB

BAACABC

AACABCB

ACABCBA

CABCBAA

)

Collar representa sólo una cuerda (

AAAAAAA

)

Pensemos en cada hilo como si representara un collar. Es decir, conectamos los dos extremos del hilo y consideramos dos hilos como el mismo collar si podemos rotar un hilo para obtener el segundo hilo; en este caso diremos que las dos cadenas son amigos. En nuestro ejemplo, las siguientes cadenas son todas amigas:

AAAAB

AAABA

AABAA

ABAAA

BAAAA

En su totalidad, cada línea de la siguiente lista corresponde a un solo collar, y la lista completa comprende las 32 cadenas.

AAAAB

AAABA

AABAA

ABAAA

BAAAA

ABBAA

AABBA

ABBAA

BBAAA

BAAAB

AABAB

ABABA

BABAA

ABAAB

BAABA

AAB

ABBBA

BBBAA

BBAAB

BAABB

ABA

BABBA

ABBAB

BBABA

BABAB

ABB

BBBBA

BBBAB

BBA

BAB

AAAAA

BBB

Observe que en la lista anterior, cada collar con más de un símbolo está representado por 5 cadenas diferentes, y la cantidad de collares representados por una sola cadena es 2, es decir, es la cantidad de símbolos distintos. Por lo tanto, la lista muestra muy claramente por qué $32 - 2$ es divisible por $5$ .

Se puede usar la siguiente regla para calcular cuántos amigos tiene una cadena determinada $S$ :

S

está construido de varias copias de la cadena

T

, y

T

no se puede descomponer en cadenas de repetición, entonces el número de amigos de

S

(incluidas

S

es igual a la longitud de

T

Por ejemplo, supongamos que empezamos con la cadena $S = ABBABBABBABB$ , que se compone de varias copias de la cadena más corta $T = ABB$ . Si rotamos un símbolo a la vez, obtenemos las siguientes 3 cadenas:

ABBAABBABB

BBABBABBA

BABBABBABAB

No hay más, porque $ABB$ tiene exactamente 3 símbolos de largo y no se puede dividir en más repeticiones instrumentos de cuerda.

Completar la prueba

Usando la regla anterior, podemos completar la demostración del pequeño teorema de Fermat con bastante facilidad, de la siguiente manera. Nuestro conjunto inicial de cadenas $a p$ se puede dividir en dos categorías:

Algunas cadenas contienen $p$ símbolos idénticos. Hay exactamente $a$ de éstos, uno para cada símbolo en el alfabeto. (En nuestro ejemplo, estas son las cuerdas $AAAAA$ y $BBB$ .)
El resto de las cuerdas usan al menos dos símbolos distintos del alfabeto. Si podemos romper $S$ en copias repetidoras de una cuerda $T$ , la longitud de $T$ debe dividir la longitud $S$ . Pero, desde la longitud $S$ es la primera $p$ , la única longitud posible $T$ también $p$ . Por lo tanto, la regla anterior nos dice que $S$ tiene exactamente $p$ amigos (incluidos $S$ en sí mismo).

La segunda categoría contiene cadenas $a p - a$ , y pueden ser dispuestas en grupos de cuerdas $p$ , un grupo para cada collar. Por lo tanto, $a p - a$ debe ser divisible por $p$ , como se prometió.

Prueba usando sistemas dinámicos

Esta demostración utiliza algunos conceptos básicos de los sistemas dinámicos.

Empezamos considerando una familia de funciones T_n(x), donde n ≥ 2 es un número entero, asignando el intervalo [0, 1] a sí mismo mediante la fórmula

<math alttext="{displaystyle T_{n}(x)={begin{cases}{nx}&0leq xTn()x)={}{}nx}0≤ ≤ x.1,1x=1,{displaystyle T_{n}(x)={begin{cases}{nx} {0leq x secuta1,1 {x=1,end{cases}}<img alt="{displaystyle T_{n}(x)={begin{cases}{nx}&0leq x

donde {y} denota la parte fraccionaria de y. Por ejemplo, la función T₃(x) se ilustra a continuación:

Se dice que un número x₀ es un punto fijo de una función f( x) si f(x₀) = x₀; en otras palabras, si f deja x₀ fijo. Los puntos fijos de una función se pueden encontrar fácilmente gráficamente: son simplemente las coordenadas x de los puntos donde la gráfica de f(x) corta la gráfica de la recta y = x. Por ejemplo, los puntos fijos de la función T₃(x) son 0, 1/2 y 1; están marcados con círculos negros en el siguiente diagrama:

Necesitaremos los siguientes dos lemas.

Lema 1. Para cualquier n ≥ 2, la función T_n(x) tiene exactamente n puntos fijos.

Prueba. Hay 3 puntos fijos en la ilustración anterior, y el mismo tipo de argumento geométrico se aplica a cualquier n ≥ 2.

Lema 2. Para cualquier entero positivo n y m, y cualquier 0 ≤ x ≤ 1,

{displaystyle T_{m}(T_{n}(x))=T_{mn}(x).}

En otras palabras, T_mn(x) es la composición de T_n(x) y T_m(x).

Demostración. La demostración de este lema no es difícil, pero debemos tener un poco de cuidado con el extremo x = 1. Para este punto, el lema es claramente verdadero, desde

{displaystyle T_{m}(T_{n}(1))=T_{m}(1)=1=T_{mn}(1).}

Supongamos que 0 ≤ x < 1. En este caso,

<math alttext="{displaystyle T_{n}(x)={nx}Tn()x)={}nx}.1,{displaystyle T_{n}(x)={nx}traducido1,}<img alt="{displaystyle T_{n}(x)={nx}

entonces T_m(T_n(x)) viene dado por

{displaystyle T_{m}(T_{n}(x))={m{nx}}.}

Por lo tanto, lo que realmente necesitamos mostrar es que

{displaystyle {m{nx}}={mnx}.}

Para ello observamos que {nx} = nx − k, donde k es el número entero parte de nx; entonces

{displaystyle {m{nx}}={mnx-mk}={mnx},}

ya que mk es un número entero.

Ahora comencemos correctamente la demostración del pequeño teorema de Fermat, estudiando la función T_a^p(x). Supondremos que a ≥ 2. Del Lema 1 sabemos que tiene puntos fijos a^p. Por el Lema 2 sabemos que

{displaystyle T_{a^{p}}(x)=underbrace {T_{a}(T_{a}(cdots T_{a}(x)cdots))} _{p{text{ times}}},}

entonces cualquier punto fijo de T_a(x) es automáticamente un punto fijo de T_a^p(x).

Nos interesan los puntos fijos de T_a^p(x) que no son puntos fijos de T_a(x ). Llamemos al conjunto de tales puntos S. Hay puntos a^p − a en S, porque por el Lema 1 nuevamente, T_a(x) tiene exactamente a puntos fijos. El siguiente diagrama ilustra la situación para a = 3 y p = 2. Los círculos negros son los puntos de S, de los cuales hay 3 ² − 3 = 6.

La idea principal de la prueba ahora es dividir el conjunto S en sus órbitas bajo T_a. Lo que esto significa es que elegimos un punto x₀ en S y aplicamos repetidamente T_a(x) a ella, para obtener la secuencia de puntos

{displaystyle x_{0},T_{a}(x_{0}),T_{a}(T_{a}(x_{0})),T_{a}(T_{a}(T_{a}(x_{0}))),ldots.}

Esta secuencia se llama la órbita de x₀ bajo T_a. Por el Lema 2, esta sucesión se puede reescribir como

x_{0},T_{a}(x_{0}),T_{a^{2}}(x_{0}),T_{a^{3}}(x_{0}),ldots.

Ya que estamos asumiendo que x₀ es un punto fijo de T_a^p(x), después de p pasos pulsamos T_a^p(x₀) = x₀, y desde ese punto en adelante la secuencia se repite.

Sin embargo, la secuencia no puede comenzar a repetirse antes de eso. Si lo hiciera, la longitud de la sección repetida tendría que ser un divisor de p, por lo que tendría que ser 1 (dado que p es primo). Pero esto contradice nuestra suposición de que x₀ no es un punto fijo de T_a.

En otras palabras, la órbita contiene exactamente p puntos distintos. Esto es válido para cada órbita de S. Por lo tanto, el conjunto S, que contiene a^p − a puntos, puede dividirse en órbitas, cada una de las cuales contiene puntos p, por lo que a^p − a es divisible por p.

(Esta prueba es esencialmente la misma que la prueba de conteo de collares dada arriba, simplemente vista a través de una lente diferente: uno puede pensar en el intervalo [0, 1] como dado por secuencias de dígitos en base a (nuestra distinción entre 0 y 1 corresponde a la distinción familiar entre representar números enteros que terminan en ".0000..." y ".9999..."). T_aⁿ equivale a desplazar dicha secuencia en n muchos dígitos. Los puntos fijos de esto serán secuencias que son cíclicas con período que divide n. En particular, los puntos fijos de T_a^p se puede considerar como los collares de longitud p, con T_aⁿ correspondiente a la rotación de dichos collares por n puntos.

Esta prueba también podría presentarse sin distinguir entre 0 y 1, simplemente usando el intervalo semiabierto [0, 1); entonces T_n solo tendría n − 1 puntos fijos, pero T_a^p − T_a seguiría siendo a^p − a, según sea necesario).

Pruebas multinomiales

Pruebas usando el teorema del binomio

Prueba 1

Esta prueba, debida a Euler, utiliza la inducción para probar el teorema para todos los números enteros $a \geq 0$ .

El paso base, que $0 p \equiv 0 (mod p)$ , es trivial A continuación, debemos demostrar que si el teorema es cierto para $a = k$ , entonces también es cierto para $a = k + 1$ . Para este paso inductivo, necesitamos el siguiente lema.

Lema. Para cualquier entero $x$ y $y$ y para cualquier primo $p$ , $(x + y) p \equiv x p + y p (mod p)$ .

El lema es un caso del sueño del estudiante de primer año. Dejando la demostración para más adelante, procedemos a la inducción.

Prueba. Asuma k^p ≡ k (mod p), y considere (k+1)^p. Por el lema tenemos

{displaystyle (k+1)^{p}equiv k^{p}+1^{p}{pmod {p}}.}

Usando la hipótesis de inducción, tenemos que k^p ≡ k (mod p); y, trivialmente, 1^p = 1. Así

{displaystyle (k+1)^{p}equiv k+1{pmod {p}},}

que es el enunciado del teorema para a = k+1. ∎

Para probar el lema, debemos introducir el teorema del binomio, que establece que para cualquier número entero positivo n,

(x+y)^{n}=sum _{i=0}^{n}{n choose i}x^{n-i}y^{i},

donde los coeficientes son los coeficientes binomiales,

{n choose i}={frac {n!}{i!(n-i)!}},

descrito en términos de la función factorial, n! = 1×2×3×⋯×n.

Prueba del Lema. Consideramos el coeficiente binomial cuando el exponente es un primo p:

{displaystyle {p choose i}={frac {p!}{i!(p-i)!}}}

Los coeficientes binomiales son todos números enteros. El numerador contiene un factor p por la definición de factorial. Cuando 0 < yo < p, ninguno de los términos en el denominador incluye un factor de p (dependiendo de la primalidad de p), dejando que el propio coeficiente posea un factor primo de p del numerador, lo que implica que

<math alttext="{displaystyle {p choose i}equiv 0{pmod {p}},qquad 0<i ()pi)↑ ↑ 0()modp),0.i.p.{displaystyle {pchoose i}equiv 0{pmodp}qquad 0 se hizo.<img alt="{p choose i}equiv 0{pmod {p}},qquad 0<i

Modulo p, esto elimina todos menos el primer y último término de la suma en el lado derecho del teorema del binomio para prima p. ∎

La primalidad de p es esencial para el lema; de lo contrario, tenemos ejemplos como

{4 choose 2}=6,

que no es divisible por 4.

Prueba 2

Usando el Lema, tenemos:

{displaystyle k^{p}equiv ((k-1)+1)^{p}equiv (k-1)^{p}+1equiv ((k-2)+1)^{p}+1equiv (k-2)^{p}+2equiv dots equiv k{pmod {p}}}

Prueba usando la expansión multinomial

La prueba, que primero fue descubierta por Leibniz (quien no la publicó) y luego redescubierta por Euler, es una aplicación muy simple del teorema multinomial, que establece

{displaystyle (x_{1}+x_{2}+cdots +x_{m})^{n}=sum _{k_{1},k_{2},dotsk_{m} atop k_{1}+k_{2}+dots +k_{m}=n}{n choose k_{1},k_{2},ldotsk_{m}}x_{1}^{k_{1}}x_{2}^{k_{2}}cdots x_{m}^{k_{m}}}

dónde

{displaystyle {n choose k_{1},k_{2},ldotsk_{m}}={frac {n!}{k_{1}!k_{2}!dots k_{m}!}}}

y la suma se toma sobre todas las secuencias de índices enteros no negativos $k 1, k 2,..., k m$ como la suma de todos $k i$ es $n$ .

Así, si expresamos $a$ como una suma de 1s (unos), obtenemos

{displaystyle a^{p}=(1+1+...+1)^{p}=sum _{k_{1},k_{2},dotsk_{a} atop k_{1}+k_{2}+dots +k_{a}=p}{p choose k_{1},k_{2},ldotsk_{a}}}

Claramente, si $p$ es primo, y si $k j$ no es igual a $p$ para cualquier $j$ , tenemos

{displaystyle {p choose k_{1},k_{2},ldotsk_{a}}equiv 0{pmod {p}},}

y si $k j$ es igual a $p$ para algunos $j$ entonces

{displaystyle {p choose k_{1},k_{2},ldotsk_{a}}=1.}

Dado que hay exactamente $a$ elementos tales que $k j = p$ para algunos $j$ , el teorema es el siguiente.

(Esta prueba es esencialmente una variante de grano más grueso de la prueba del conteo de collares dada anteriormente; los coeficientes multinomiales cuentan el número de formas en que una cadena se puede permutar en anagramas arbitrarios, mientras que el argumento del collar cuenta el número de formas en que una cadena se puede rotar en anagramas cíclicos. Es decir, que los coeficientes multinomiales no triviales aquí son divisibles por $p$ puede verse como una consecuencia del hecho que cada collar no trivial de longitud $p$ se puede desenvolver en una cadena en $p$ muchas maneras.

Esta expansión multinomial también es, por supuesto, lo que esencialmente subyace a la prueba basada en el teorema binomial anterior)

Prueba usando expansiones de productos de potencia

Giedrius Alkauskas proporcionó una prueba combinatoria aditiva basada en expansiones formales de productos de energía. Esta demostración no utiliza el algoritmo de Euclides ni el teorema del binomio, sino que emplea series de potencias formales con coeficientes racionales.

Demostración como caso particular del teorema de Euler

Esta demostración, descubierta por James Ivory y redescubierta por Dirichlet, requiere cierta experiencia en aritmética modular.

Supongamos que $a$ es positivo y no divisible por $p . La idea es que si escribimos la secuencia de números$

{displaystyle a,2a,3a,ldots(p-1)a}

()A)

y reduce cada módulo $p$ , la secuencia resultante resulta ser un reordenamiento de

{displaystyle 1,2,3,ldotsp-1.}

()B)

Por lo tanto, si multiplicamos los números de cada secuencia, los resultados deben ser idénticos módulo $p$ :

atimes 2atimes 3atimes cdots times (p-1)aequiv 1times 2times 3times cdots times (p-1){pmod {p}}.

Recopilar los términos $a$ da como resultado

a^{p-1}(p-1)!equiv (p-1)!{pmod {p}}.

Finalmente, podemos "cancelar" los números $1, 2,..., p - 1$ de ambos lados de esta ecuación, obtención

a^{p-1} equiv 1 pmod p.

Hay dos pasos en la prueba anterior que necesitamos justificar:

Por qué los elementos de la secuencia (A), modulo reducido $p$ , son una reorganización de (B), y
Por qué es válido “cancel” en la configuración de aritmética modular.

Probaremos estas cosas a continuación; Veamos primero un ejemplo de esta prueba en acción.

Un ejemplo

Si $a = 3$ y $p = 7$ , entonces la sucesión en cuestión es

{displaystyle 3,6,9,12,15,18;}

reducir módulo 7 da

{displaystyle 3,6,2,5,1,4,}

que es solo un reordenamiento de

{displaystyle 1,2,3,4,5,6.}

Multiplicarlos juntos da

{displaystyle 3times 6times 9times 12times 15times 18equiv 3times 6times 2times 5times 1times 4equiv 1times 2times 3times 4times 5times 6{pmod {7}};}

es decir,

{displaystyle 3^{6}(1times 2times 3times 4times 5times 6)equiv (1times 2times 3times 4times 5times 6){pmod {7}}.}

Al cancelar 1 × 2 × 3 × 4 × 5 × 6 se obtiene

{displaystyle 3^{6}equiv 1{pmod {7}},}

que es el pequeño teorema de Fermat para el caso $a = 3$ y $p = 7$ .

La ley de cancelación

Primero expliquemos por qué es válido, en determinadas situaciones, "cancelar". La declaración exacta es la siguiente. Si $u$ , $x$ y $y$ son números enteros, y $u$ no es divisible por un número primo $p$ , y si

{displaystyle uxequiv uy{pmod {p}},}

()C)

entonces podemos "cancelar" $u$ para obtener

{displaystyle xequiv y{pmod {p}}.}

()D)

Nuestro uso de esta ley de cancelación en la demostración anterior del pequeño teorema de Fermat era válido, porque los números $1, 2,..., p - 1$ ciertamente no son divisibles por $p$ (de hecho, son menores que $p$ ).

Podemos demostrar fácilmente la ley de cancelación usando el lema de Euclides, que generalmente establece que si un primo $p$ divide un producto $ab$ (donde $a$ y $b$ son números enteros), entonces $p$ debe dividir $a$ o $b$ . De hecho, la afirmación (C) simplemente significa que $p$ divide $ux - uy = u (x - y)$ . Dado que $p$ es un número primo que no divide a $u$ , Euclides& El lema del #39 nos dice que debe dividir $x - y$ en su lugar; es decir, (D) se cumple.

Tenga en cuenta que las condiciones bajo las cuales se cumple la ley de cancelación son bastante estrictas, y esto explica por qué el pequeño teorema de Fermat exige que $p$ es un número primo. Por ejemplo, $2\times2 \equiv 2\times5 (mod 6)$ , pero no es cierto que $2 \equiv 5 (mod 6). Sin embargo, se cumple la siguiente generalización de la ley de cancelación: si u, x, y y z son números enteros, si u y z son relativamente primos, y si$

{displaystyle uxequiv uy{pmod {z}},}

entonces podemos "cancelar" $u$ para obtener

{displaystyle xequiv y{pmod {z}}.}

Esto se deriva de una generalización del lema de Euclides.

La propiedad de reordenamiento

Finalmente, debemos explicar por qué la secuencia

{displaystyle a,2a,3a,ldots(p-1)a,}

cuando se reduce el módulo p, se convierte en un reordenamiento de la secuencia

{displaystyle 1,2,3,ldotsp-1.}

Para empezar, ninguno de los términos $a$ , $2 a$ ,..., $(p - 1) a$ puede ser congruente con módulo cero $p$ , ya que si $k$ es uno de los números $1, 2,..., p - 1$ , entonces $k$ es relativamente primo con $p$ , y también lo es $a$ , entonces Euclid' El lema nos dice que $ka$ no comparte ningún factor con $p$ . Por lo tanto, al menos sabemos que los números $a$ , $2 a$ ,..., $(p - 1) a$ , cuando se reduce el módulo $p$ , debe encontrarse entre los números $1, 2, 3,..., p - 1$ .

Además, los números $a$ , $2 a$ ,..., $(p - 1) a$ deben ser todos distintos después de reducirlos módulo $p$ , porque si

{displaystyle kaequiv ma{pmod {p}},}

donde $k$ y $m$ son uno de $1, 2,..., p - 1$ , entonces la ley de cancelación nos dice que

{displaystyle kequiv m{pmod {p}}.}

Dado que tanto $k$ como $m$ están entre $1$ y $p - 1$ , deben ser iguales. Por lo tanto, los términos $a$ , $2 a$ ,..., $(p - 1) a$ cuando se reduce el módulo $p$ debe ser distinto. Para resumir: cuando reducimos los números $p - 1$ $a$ , $2 a$ ,..., $(p - 1) a$ módulo $p$ , obtenemos distintos miembros de la secuencia $1$ , $2$ ,..., $p - 1$ . Dado que hay exactamente $p - 1$ de estos, la única posibilidad es que los primeros sean una reorganización de los últimos.

Aplicaciones al teorema de Euler

Este método también se puede usar para demostrar el teorema de Euler, con una ligera alteración en los números de $1$ a $p - 1$ se sustituyen por los números menores que y coprimos con algún número $m$ (no necesariamente primo). Tanto la propiedad de reordenación como la ley de cancelación (bajo la forma generalizada mencionada anteriormente) todavía se cumplen y pueden utilizarse.

Por ejemplo, si $m = 10$ , entonces los números menores que $m$ y coprimos con $m$ son $1$ , $3$ , $7$ y $9$ . Así tenemos:

{displaystyle atimes 3atimes 7atimes 9aequiv 1times 3times 7times 9{pmod {10}}.}

Por lo tanto,

{displaystyle {a^{varphi (10)}}equiv 1{pmod {10}}.}

La prueba como corolario del criterio de Euler

Pruebas usando la teoría de grupos

Prueba estándar

Esta prueba requiere los elementos más básicos de la teoría de grupos.

La idea es reconocer que el conjunto $G = {1, 2, \dots, p - 1$ }, con la operación de multiplicación (tomada módulo $p$ ), forma un grupo. El único axioma de grupo que requiere algo de esfuerzo para verificar es que cada elemento de $G$ es invertible. Tomando esto con fe por el momento, supongamos que $a$ está en el rango $1 \leq a \leq p - 1$ , es decir, $a$ es un elemento de $G$ . Sea $k$ el orden de $a$ , es decir, $k$ es el entero positivo más pequeño tal que $a k \equiv 1 (mod p)$ . Luego los números $1, a, a 2,..., a k -1$ módulo reducido $p$ forman un subgrupo de $G$ cuyo orden es $k$ y por lo tanto, por Lagrange's teorema, $k$ divide el orden de $G$ , que es p − 1. Entonces $p - 1 = km$ para algún entero positivo $m$ y luego

{displaystyle a^{p-1}equiv a^{km}equiv (a^{k})^{m}equiv 1^{m}equiv 1{pmod {p}}.}

Para demostrar que todo elemento $b$ de $G$ es invertible, podemos proceder de la siguiente manera. Primero, $b$ es coprimo con $p$ . Así, la identidad de Bézout nos asegura que hay números enteros $x$ y $y$ tal que $bx + py = 1$ . Leyendo este módulo de igualdad $p$ , vemos que $x$ es un inversa para $b$ , ya que $bx \equiv 1 (mod p)$ . Por lo tanto, cada elemento de $G$ es invertible. Entonces, como se comentó anteriormente, $G$ es un grupo.

Por ejemplo, cuando $p = 11$ , los inversos de cada elemento se dan de la siguiente manera:

$a$	1	2	3	4	5	6	7	8	9	10
$a -1$	1	6	4	3	9	2	8	7	5	10

Prueba de Euler

Si tomamos la prueba anterior y, en lugar de usar el teorema de Lagrange, tratamos de demostrarlo en esta situación específica, entonces obtenemos la tercera prueba de Euler, que es la que encontró más natural. Sea $A$ el conjunto cuyos elementos son los números $1, a, a 2,..., a k - 1$ módulo reducido $p$ . Si $A = G$ , entonces $k = p - 1$ y, por lo tanto, $k$ divide a $p -1$ . De lo contrario, hay algo de $b 1 \in G A$ .

Sea $A 1$ el conjunto cuyos elementos son los números $b 1, ab 1, a 2 b 1, \dots, a k - 1 b 1$ módulo reducido $p$ . Entonces $A 1$ tiene $k$ elementos distintos, porque de lo contrario habría dos números distintos $m, n \in {0, 1,..., k - 1$ } tal que $a m b 1 \equiv a n b 1 (mod p)$ , lo cual es imposible, ya que seguiría que $a m \equiv a n (modificación p). Por otro lado, ningún elemento de A 1 puede ser un elemento de A, porque de lo contrario habría números m, n \in {0, 1, \dots, k - 1} tal que a m b 1 \equiv a n (modificación p), y luego b 1 \equiv a n a k - m \equiv a n + k - m (mod p), lo cual es imposible, ya que b 1 \notin A .$

Entonces, el conjunto $A \cup A 1$ tiene $2 k$ elementos. Si resulta ser igual a G, entonces $2 k = p -1$ y por lo tanto $k$ divide $p -1$ . De lo contrario, hay algo de $b 2 \in G (A \cup A 1)$ y podemos empezar de nuevo, definiendo $A 2$ como el conjunto cuyos elementos son los números $b 2, ab 2, a 2 b 2,..., a k - 1 b 2$ módulo reducido $p$ . Dado que $G$ es finito, este proceso debe detenerse en algún punto y esto prueba que $k$ divide $p - 1$ .

Por ejemplo, si $a = 5$ y $p = 13$ , entonces, ya que

$52 = 25 \equiv 12 (mod 13)$ ,
$53 = 125 \equiv 8 (mod 13)$ ,
$54 1 (mod 13)$ ,

tenemos $k = 4$ y $A = {1, 5, 8, 12$ }. Claramente, $A \neq G = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12$ }. Sea $b 1$ un elemento de $G A$ ; por ejemplo, tome $b 1 = 2$ . Entonces, desde

$2\times1 = 2$ ,
$2\times5 = 10$ ,
$2\times8 = 16 ngel 3 (mod 13)$ ,
$2\times12 = 24 ngel 11 (mod 13)$ ,

tenemos $A 1 = {2, 3, 10, 11$ }. Claramente, $A \cup A 1 \neq G$ . Sea $b 2$ un elemento de $G (A \cup A 1)$ ; por ejemplo, tome $b 2 = 4$ . Entonces, desde

$4\times1 = 4$ ,
$4\times5 = 20 ngel 7 (mod 13)$ ,
$4\times8 = 32 ngel 6 (mod 13)$ ,
$4\times12 = 48 ngel 9 (mod 13)$ ,

tenemos $A 2 = {4, 6, 7, 9$ }. Y ahora $G = A \cup A 1 \cup A 2$ .

Tenga en cuenta que los conjuntos $A$ , $A 1$ , y así sucesivamente son de hecho las clases laterales de $A$ en $G$ .

Contenido relacionado

Más resultados...