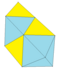
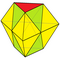
Deltaedro

En geometría, un deltaedro (plural deltaedro) es un poliedro cuyas caras son todas triángulos equiláteros. El nombre proviene de la mayúscula griega delta (Δ), que tiene la forma de un triángulo equilátero. Hay infinitos deltaedros, y todos tienen un número par de caras según el lema del apretón de manos. De estos sólo ocho son convexos y tienen 4, 6, 8, 10, 12, 14, 16 y 20 caras. El número de caras, aristas y vértices se enumera a continuación para cada uno de los ocho deltaedros convexos.

Los ocho deltaedros convexos

Solo hay ocho deltaedros estrictamente convexos: tres son poliedros regulares y cinco son sólidos de Johnson. Los tres poliedros regulares convexos son de hecho sólidos platónicos.

Regular deltahedra
Imagen	Nombre	Caras	Edges	Vertices	Configuraciones de Vertex	Grupo de Symmetry
	tetrahedron	4	6	4	4 × 33	Td[3,3]
	octaedro	8	12	6	6 × 34	Oh[4,3]
	icosahedron	20	30	12	12 × 35	Ih[5,3]
Johnson deltahedra
Imagen	Nombre	Caras	Edges	Vertices	Configuraciones de Vertex	Grupo de Symmetry
	Bipyramid triangular	6	9	5	2 × 33 3 × 34	D3h[3,2]
	pentagonal bipyramid	10	15	7	5 × 34 2 × 35	D5h[5,2]
	snub disphenoid	12	18	8	4 × 34 4 × 35	D2d[2,2]
	prisma triangular triaugmentado	14	21	9	3 × 34 6 × 35	D3h[3,2]
	bipyramid cuadrado	16	24	10	2 × 34 8 × 35	D4d[4,2]

En el deltaedro de 6 caras, algunos vértices tienen grado 3 y algunos grado 4. En los deltaedros de 10, 12, 14 y 16 caras, algunos vértices tienen grado 4 y algunos grado 5. Estos cinco deltaedros irregulares Los deltaedros pertenecen a la clase de sólidos de Johnson: poliedros convexos con polígonos regulares por caras.

Los deltaedros conservan su forma incluso si los bordes pueden girar libremente alrededor de sus vértices, de modo que los ángulos entre los bordes sean fluidos. No todos los poliedros tienen esta propiedad: por ejemplo, si algunos de los ángulos de un cubo se relajan, el cubo puede deformarse y convertirse en un prisma cuadrado no recto.

No existe un deltaedro convexo de 18 caras. Sin embargo, el icosaedro de aristas contraídas da un ejemplo de un octadecaedro que puede hacerse convexo con 18 caras triangulares irregulares o con triángulos equiláteros que incluyen dos conjuntos coplanares de tres triángulos.

Casos no estrictamente convexos

Hay infinitamente muchos casos con triángulos coplanar, permitiendo secciones de los azulejos triangulares infinitos. Si los conjuntos de triángulos coplanar se consideran una sola cara, se puede contar un conjunto más pequeño de caras, bordes y vértices. Las caras triangulares coplanar se pueden fusionar en caras rhombic, trapezoidal, hexagonal u otros poligonales equiláteros. Cada cara debe ser un polígono convexo como , , , , , , y ,...

Algunos ejemplos más pequeños incluyen:

Coplanar deltahedra

Imagen	Nombre	Caras	Edges	Vertices	Configuraciones de Vertex	Grupo de Symmetry
	Aumentado octaedro Aumento 1 tet + 1 oct	10	15	7	1 × 33 3 × 34 3 × 35 0 × 36	C3v, [3]
		4 3	12
	Trigonal trapezohedron Aumento 2 tets + 1 oct	12	18	8	2 × 33 0 × 34 6 × 35 0 × 36	C3v, [3]
		6	12
	Aumento 2 tets + 1 oct	12	18	8	2 × 33 1 × 34 4 × 35 1 × 36	C2v, [2]
		2 2 2	11	7
	frusto triangular Aumento 3 tets + 1 oct	14	21	9	3 × 33 0 × 34 3 × 35 3 × 36	C3v, [3]
		1 3 1	9	6
	Elongated octahedron Aumento 2 tets + 2 octs	16	24	10	0 × 33 4 × 34 4 × 35 2 × 36	D2h[2,2]
		4 4	12	6
	Tetraedro Aumento 4 tets + 1 oct	16	24	10	4 × 33 0 × 34 0 × 35 6 × 36	Td[3,3]
		4	6	4
	Aumento 3 tets + 2 octs	18	27	11	1 × 33 2 × 34 5 × 35 3 × 36	D2h[2,2]
		2 1 2 2	14	9
	Edge-contractedron	18	27	11	0 × 33 2 × 34 8 × 35 1 × 36	C2v, [2]
		12 2	22	10
	Birusto triangular Aumento 6 tets + 2 octs	20	30	12	0 × 33 3 × 34 6 × 35 3 × 36	D3h[3,2]
		2 6	15	9
	cúpula triangular Aumento 4 tets + 3 octs	22	33	13	0 × 33 3 × 34 6 × 35 4 × 36	C3v, [3]
		3 3 1 1	15	9
	Bipirámide triangular Aumento 8 tets + 2 octs	24	36	14	2 × 33 3 × 34 0 × 35 9 × 36	D3h, [3]
		6	9	5
	Antiprisma hexagonal	24	36	14	0 × 33 0 × 34 12 × 35 2 × 36	D6d[12,2]+]
		12 2	24	12
	Truncated tetrahedron Aumento 6 tets + 4 octs	28	42	16	0 × 33 0 × 34 12 × 35 4 × 36	Td[3,3]
		4 4	18	12
	Tetrakis cuboctahedron Octahedron Aumento 8 tets + 6 octs	32	48	18	0 × 33 12 × 34 0 × 35 6 × 36	Oh[4,3]
		8	12	6

Formas no convexas

Existe un número infinito de formas no convexas.

Algunos ejemplos de deltaedros que se cruzan con caras:

• Great icosahedron - un sólido Kepler-Poinsot, con 20 triángulos intersectiendo

  

Se pueden generar otros deltaedros no convexos agregando pirámides equiláteras a las caras de los 5 sólidos platónicos:

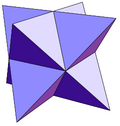triakis tetrahedron	tetrakis hexahedron	triakis octahedron (stella octangula)	pentakis dodecahedron	triakis icosahedron
12 triángulos	24 triángulos		60 triángulos

Otros aumentos del tetraedro incluyen:

Tetrahedra aumentada

8 triángulos	10 triángulos	12 triángulos

También agregando pirámides invertidas a las caras:

• Excavado dodecaedro

Excavado dodecaedro	A toroidal deltahedron
60 triángulos	48 triángulos