Deformación dinámica del tiempo

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Un algoritmo para medir la similitud entre dos secuencias temporales, que pueden variar en velocidad

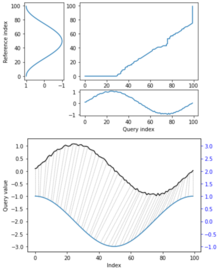
En el análisis de series temporales, la distorsión temporal dinámica (DTW) es un algoritmo para medir la similitud entre dos secuencias temporales, que pueden variar en velocidad. Por ejemplo, las similitudes al caminar podrían detectarse usando DTW, incluso si una persona caminaba más rápido que la otra, o si hubo aceleraciones y desaceleraciones durante el curso de una observación. DTW se ha aplicado a secuencias temporales de datos de video, audio y gráficos; de hecho, cualquier dato que pueda convertirse en una secuencia unidimensional puede analizarse con DTW. Una aplicación muy conocida ha sido el reconocimiento automático de voz, para hacer frente a diferentes velocidades de habla. Otras aplicaciones incluyen el reconocimiento de hablantes y el reconocimiento de firmas en línea. También se puede utilizar en aplicaciones de coincidencia de formas parciales.

En general, DTW es un método que calcula una coincidencia óptima entre dos secuencias dadas (por ejemplo, series de tiempo) con ciertas restricciones y reglas:

Cada índice de la primera secuencia debe ser igualado con uno o más índices de la otra secuencia, y viceversa
El primer índice de la primera secuencia debe coincidir con el primer índice de la otra secuencia (pero no tiene que ser su único partido)
El último índice de la primera secuencia debe coincidir con el último índice de la otra secuencia (pero no tiene que ser su único partido)
El mapeo de los índices de la primera secuencia a los índices de la otra secuencia debe estar aumentando monotonicamente, y viceversa, es decir, si $i}" xmlns="http://www.w3.org/1998/Math/MathML">j■i{displaystyle j]i}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/fb45e6bd25f2486ca8b3052e74e27c11fa0d1761" style="vertical-align: -0.671ex; margin-left: -0.027ex; width:4.886ex; height:2.509ex;"/>$ son índices de la primera secuencia, entonces no debe haber dos índices $k}" xmlns="http://www.w3.org/1998/Math/MathML">l■k{displaystyle l espírituk}k}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/688c6a57b28eb2e1fdcb26077b751a3f07eb95d9" style="vertical-align: -0.338ex; width:5.003ex; height:2.176ex;"/>$ en la otra secuencia, tal índice $i$ se combina con el índice $l$ índice $j$ se combina con el índice $k$ , y viceversa

Podemos trazar cada partido entre las secuencias ${displaystyle 1:M}$ y ${displaystyle 1:N}$ como un camino en un $Mtimes N$ matriz $(1,1)$ a $(M,N)$ , tal que cada paso es uno de ${displaystyle (0,1),(1,0),(1,1)}$ . En esta formulación, vemos que el número de posibles partidos es el número Delannoy.

La coincidencia óptima se denota por la coincidencia que satisface todas las restricciones y reglas y que tiene el costo mínimo, donde el costo se calcula como la suma de las diferencias absolutas, para cada par de índices coincidentes, entre sus valores.

Las secuencias están "distorsionadas" no linealmente en la dimensión temporal para determinar una medida de su similitud independiente de ciertas variaciones no lineales en la dimensión temporal. Este método de alineación de secuencias se usa a menudo en la clasificación de series temporales. Aunque DTW mide una cantidad similar a la distancia entre dos secuencias dadas, no garantiza que se mantenga la desigualdad del triángulo.

Además de una medida de similitud entre las dos secuencias, la llamada "ruta de deformación" es producido. Al deformarse según este camino, las dos señales pueden alinearse en el tiempo. La señal con un conjunto original de puntos X(original), Y(original) se transforma en X(alabeada), Y (alabeado). Esto encuentra aplicaciones en secuencias genéticas y sincronización de audio. En una técnica relacionada, las secuencias de velocidad variable se pueden promediar usando esta técnica, consulte la sección de secuencia promedio.

Conceptualmente, es muy similar al algoritmo de Needleman-Wunsch.

Implementación

Este ejemplo ilustra la implementación del algoritmo de temporización dinámica cuando las dos secuencias s y t son cuerdas de símbolos discretos. Para dos símbolos x y Sí., d(x, y) es una distancia entre los símbolos, por ejemplo. d(x, y) = $| x - y |$ .

int DTWDistance(s: array [1..n], t: array [1..m] {}
DTW:= array [0.n, 0.m]

para i:= 0 a n
para j:= 0 a m
DTW[i, j]:= infinity
DTW[0, 0]:= 0

para i:= 1 a n
para j:= 1 a m
costo:= d(s[i], t[j])
DTW[i, j]:= costo + mínimo(DTW[i-1, j ], // inserción
DTW[i j-1], // deletion
DTW[i-1, j-1]) // partido

devolver DTW[n, m]
}

donde DTW[i, j] es la distancia entre s[1:i] y t[1:j] con el mejor alineación.

A veces queremos añadir una limitación local. Es decir, lo necesitamos si s[i] se combina con t[j], entonces $| i - j |$ no es más grande que wUn parámetro ventana.

Podemos modificar fácilmente el algoritmo anterior para agregar una limitación de localidad (diferencias) marcado). Sin embargo, la modificación anterior sólo funciona si $| n - m |$ no es más grande que w, es decir, el punto final está dentro de la longitud de la ventana desde diagonal. Para que el algoritmo funcione, el parámetro ventana w debe adaptarse para que $| n - m | le w$ (ver la línea marcada con (*) en el código).

int DTWDistance(s: array [1..n], t: array [1..m], w: int♪
DTW:= array [0.n, 0.m]

 w:= max(w, abs(n-m)) // adapt window size (*)

para i:= 0 a n
para j:= 0 a m
DTW[i, j]:= infinity
DTW[0, 0]:= 0
 para i:= 1 a n para j:= max(1, i-w) a min(m, i+w) DTW[i, j]:= 0para i:= 1 a n
para j:= max(1, i-w) a min(m, i+w)costo:= d(s[i], t[j])
DTW[i, j]:= costo + mínimo(DTW[i-1, j ], // inserción
DTW[i j-1], // deletion
DTW[i-1, j-1]) // partido
devolver DTW[n, m]
}

Propiedades de deformación

El algoritmo DTW produce una coincidencia discreta entre los elementos existentes de una serie a otra. En otras palabras, no permite escalar el tiempo de los segmentos dentro de la secuencia. Otros métodos permiten la deformación continua. Por ejemplo, la deformación optimizada de correlación (COW) divide la secuencia en segmentos uniformes que se escalan en el tiempo mediante interpolación lineal para producir la mejor deformación coincidente. La escala del segmento provoca la creación potencial de nuevos elementos, al escalar el tiempo de los segmentos hacia abajo o hacia arriba y, por lo tanto, produce una deformación más sensible que la coincidencia discreta de elementos sin procesar de DTW.

Complejidad

La complejidad del tiempo del algoritmo DTW es $O(NM)$ , donde $N$ y $M$ son las longitudes de las dos secuencias de entrada. El tiempo cuadrático de 50 años se rompió en 2016: un algoritmo debido a Gold y Sharir permite computar DTW en ${displaystyle O({N^{2}}/log log N)}$ tiempo y espacio para dos secuencias de entrada de longitud $N$ . Este algoritmo también se puede adaptar a secuencias de diferentes longitudes. A pesar de esta mejora, se demostró que un tiempo de ejecución fuertemente subcuadrático de la forma ${displaystyle O(N^{2-epsilon })}$ para algunos $0}" xmlns="http://www.w3.org/1998/Math/MathML">ε ε ■0{displaystyle epsilon }0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/568095ad3924314374a5ab68fae17343661f2a71" style="vertical-align: -0.338ex; width:5.205ex; height:2.176ex;"/>$ no puede existir a menos que la hipótesis de tiempo exponencial Fuerte falle.

Mientras que el algoritmo de programación dinámico para DTW requiere $O(NM)$ espacio en una aplicación ingenua, el consumo espacial puede reducirse a ${displaystyle O(min(N,M))}$ usando el algoritmo de Hirschberg.

Cálculo rápido

Did you mean:

Fast techniques for computing DTW include Early Abandoned and Pruned DTW, Pruned DTW, Sparse DTW, FastDTW, and the Multiscale DTW.

Una tarea común, la recuperación de series temporales similares, se puede acelerar mediante el uso de límites inferiores como LB_Keogh, LB_Improved, LB_Enhanced, LB_Webb o LB_Petitjean. Sin embargo, el algoritmo DTW de abandono anticipado y podado reduce el grado de aceleración que proporciona el límite inferior y, a veces, lo vuelve ineficaz.

En una encuesta, Wang et al. informaron resultados ligeramente mejores con el límite inferior LB_Improved que con el límite LB_Keogh, y encontraron que otras técnicas eran ineficientes. Posteriormente a esta encuesta, se desarrolló el límite LB_Enhanced que siempre es más estricto que LB_Keogh y, al mismo tiempo, es más eficiente de calcular. LB_Petitjean es el límite inferior conocido más ajustado que se puede calcular en tiempo lineal.

Secuencia media

La promediación de la deformación dinámica del tiempo es el problema de encontrar una secuencia promedio para un conjunto de secuencias. NLAAF es un método exacto para promediar dos secuencias usando DTW. Para más de dos secuencias, el problema está relacionado con el de la alineación múltiple y requiere heurística. DBA es actualmente un método de referencia para promediar un conjunto de secuencias consistentemente con DTW. COMASA aleatoriza eficientemente la búsqueda de la secuencia promedio, utilizando DBA como proceso de optimización local.

Aprendizaje supervisado

Un clasificador de vecino más cercano puede lograr un rendimiento de última generación cuando se utiliza la deformación temporal dinámica como medida de distancia.

Deformación dinámica del tiempo de Amerced

Amerced Dynamic Time Warping (ADTW) es una variante de DTW diseñada para controlar mejor la permisividad de DTW en las alineaciones que permite. Las ventanas que usa el DTW clásico para restringir las alineaciones introducen una función de paso. Cualquier deformación del camino está permitida dentro de la ventana y ninguna más allá. Por el contrario, ADTW emplea una penalización aditiva que se incurre cada vez que se deforma la ruta. Se permite cualquier cantidad de deformación, pero cada acción de deformación incurre en una penalización directa. ADTW supera significativamente a DTW con ventanas cuando se aplica como un clasificador vecino más cercano en un conjunto de tareas de clasificación de series temporales de referencia.

Deformación gráfica del tiempo

Graphical Time Warping (GTW) es una versión generalizada de DTW que puede alinear varios pares de series temporales o secuencias de forma conjunta. En comparación con la alineación de varios pares de forma independiente a través de DTW, GTW considera tanto la precisión de alineación de cada par de secuencias (como DTW) como la similitud entre pares (según la estructura de datos o asignada por el usuario). Esto puede dar como resultado un mejor rendimiento de alineación cuando existe la similitud entre los pares.

Funciones de distancia

DTW es sensible a la función de distancia d(x, y) utilizado para marcar partidos entre pares de valores en las dos secuencias. La definición original de DTW utilizada d(x, y) = $| x - y |$ . En la clasificación de series temporales, d(x, y) = ${displaystyle (x-y)^{2}}$ se ha vuelto popular.

El trabajo reciente ha demostrado que el ajuste de esta medida de distancia puede ser útil para ajustar el rendimiento de DTW. Específicamente, sintonización $gamma$ en una familia de funciones de distancia de la forma d(x, y) = ${displaystyle |x-y|^{gamma }}$ hace que DTW se centre más en los efectos de baja amplitud cuando $gamma$ es pequeños y grandes efectos de amplitud cuando $gamma$ es grande.

Enfoques alternativos

En el análisis de datos funcionales, las series de tiempo se consideran discretizaciones de funciones suaves (diferenciables) de tiempo. Al ver las muestras observadas en funciones uniformes, se pueden utilizar matemáticas continuas para analizar datos. La suavidad y la monotonicidad de las funciones de distorsión temporal se pueden obtener, por ejemplo, integrando una función de base radial variable en el tiempo, siendo así un difeomorfismo unidimensional. Las funciones de deformación de tiempo no lineales óptimas se calculan minimizando una medida de distancia del conjunto de funciones a su promedio deformado. Se pueden agregar términos de penalización por rugosidad para las funciones de alabeo, por ejemplo, restringiendo el tamaño de su curvatura. Las funciones de deformación resultantes son suaves, lo que facilita el procesamiento posterior. Este enfoque se ha aplicado con éxito para analizar los patrones y la variabilidad de los movimientos del habla.

Otro enfoque relacionado son los modelos ocultos de Markov (HMM) y se ha demostrado que el algoritmo de Viterbi utilizado para buscar la ruta más probable a través del HMM es equivalente al DTW estocástico.

El DTW y los métodos de deformación relacionados se suelen utilizar como pasos previos o posteriores al procesamiento en los análisis de datos. Si las secuencias observadas contienen variación aleatoria en sus valores, la forma de las secuencias observadas y la desalineación temporal aleatoria, la deformación puede sobreajustarse al ruido y generar resultados sesgados. Una formulación de modelo simultánea con variación aleatoria en ambos valores (vertical) y parametrización de tiempo (horizontal) es un ejemplo de un modelo de efectos mixtos no lineal. En el análisis del movimiento humano, se ha demostrado que el modelado de efectos mixtos no lineales simultáneos produce resultados superiores en comparación con DTW.

Software de código abierto

La biblioteca tempo C++ con unión Python implementa Early Abandoned and Pruned DTW, así como Early Abandoned y Pruned ADTW y DTW límites inferiores LB_Keogh, LB_Enhanced y LB_Webb.
El UltraFastMPSearch Biblioteca Java implementa el algoritmo UltraFastWWSearch para el ajuste rápido de la ventana de calentamiento.
La biblioteca Ibimproved C++ implementa Fast Nearest-Neighbor Retrieval algoritmos bajo GNU General Public License (GPL). También proporciona una implementación de C++ de la gestión dinámica del tiempo, así como varios límites inferiores.
El Rápido DTW biblioteca es una implementación Java de DTW y una implementación FastDTW que proporciona alineaciones óptimas o casi óptimas con una O()N) tiempo y complejidad de la memoria, en contraste con la O()N²) requisito para el algoritmo DTW estándar. FastDTW utiliza un enfoque multinivel que proyecta recursivamente una solución de una resolución más gruesa y perfecciona la solución proyectada.
FastDTW tenedor (Java) publicado en Maven Central.
time-series-classification (Java) un paquete para la clasificación de series de tiempo utilizando DTW en Weka.
La suite DTW proporciona paquetes Python (dtw-python) y R (dtw) con una cobertura integral de los miembros de la familia del algoritmo DTW, incluyendo una variedad de reglas de recursión (también llamadas patrones de paso), restricciones y subestring matching.
La biblioteca de Python de mlpy implementa DTW.
La biblioteca pidtw Python implementa las medidas DTW de Manhattan y Euclidean, incluyendo los límites inferiores LB_Keogh.
La biblioteca cudadtw C++/CUDA implementa alineación de subsequencia del DTW de Euclideano y z- distancia euclidiana normalizada similar a la popular UCR-Suite en aceleradores compatibles con CUDA.
Java La biblioteca de aprendizaje automático ML implementa DTW.
La biblioteca ndtw C# implementa DTW con varias opciones.
Sketch-a-Char utiliza Greedy DTW (ejecutado en JavaScript) como parte del programa de clasificación de símbolos LaTeX.
El MatchBox implementa DTW para que coincida con los coeficientes cepstral de frecuencia mel de las señales de audio.
Secuencia promedio: una implementación GPL Java de DBA.
The Gesture Recognition Toolkit imperGRT C+++ real-time gesto-recognition toolkit implementa DTW.
El paquete de software PyHubs implementa DTW y clasificadores de vecinos más cercanos, así como sus extensiones (clasificadores de conocimiento de la cordura).
La sencilla biblioteca Python implementa el clásico O()NM) algoritmo de programación dinámica y bases en Numpy. Soporta valores de cualquier dimensión, así como el uso de funciones de norma personalizadas para las distancias. Está licenciada bajo la licencia MIT.
La biblioteca de tslearn Python implementa DTW en el contexto de las series temporales.
La culata La biblioteca Python implementa un estado del arte mejorado Time Warp Edit Distancia utilizando sólo la memoria lineal con velocidades fenomenales.
DynamicAxisWarping.jl Es una aplicación Julia de DTW y algoritmos relacionados como FastDTW, SoftDTW, GeneralDTW y DTW barycenters.
El Multi_DTW implementa DTW para combinar dos arrays de 1-D o archivos de 2-D de discurso (2-D array).

Aplicaciones

Reconocimiento de palabras habladas

Debido a las diferentes velocidades de habla, se produce una fluctuación no lineal en el patrón de habla frente al eje de tiempo, que debe eliminarse. La coincidencia de DP es un algoritmo de coincidencia de patrones basado en programación dinámica (DP), que utiliza un efecto de normalización de tiempo, donde las fluctuaciones en el eje de tiempo se modelan mediante una función de distorsión de tiempo no lineal. Considerando dos patrones de habla cualesquiera, podemos deshacernos de sus diferencias de tiempo deformando el eje de tiempo de uno para que se logre la máxima coincidencia con el otro. Además, si se permite que la función de deformación tome cualquier valor posible, se puede hacer muy poca distinción entre palabras pertenecientes a diferentes categorías. Entonces, para mejorar la distinción entre palabras pertenecientes a diferentes categorías, se impusieron restricciones en la pendiente de la función de deformación.

Análisis de poder de correlación

Los relojes inestables se utilizan para vencer el análisis de potencia ingenuo. Se utilizan varias técnicas para contrarrestar esta defensa, una de las cuales es la deformación dinámica del tiempo.

Finanzas y econometría

La distorsión temporal dinámica se utiliza en finanzas y econometría para evaluar la calidad de la predicción en comparación con los datos del mundo real.

Contenido relacionado

Más resultados...