Deferente y epiciclo
En los sistemas astronómicos hipparquiano, ptolemaico y copernicano, el epiciclo (del griego antiguo ἐπίκυκλος (epíkuklos) 'sobre el círculo', que significa &# 34;círculo que se mueve sobre otro círculo") era un modelo geométrico utilizado para explicar las variaciones en la velocidad y la dirección del movimiento aparente de la Luna, el Sol y los planetas. En particular, explicó el aparente movimiento retrógrado de los cinco planetas conocidos en ese momento. En segundo lugar, también explicaba los cambios en las distancias aparentes de los planetas a la Tierra.
Fue propuesta por primera vez por Apolonio de Perge a finales del siglo III a. Fue desarrollado por Apolonio de Perga e Hiparco de Rodas, quienes lo usaron extensamente durante el siglo II a. C., luego lo formalizaron y lo usaron extensamente Ptolomeo en su tratado astronómico del siglo II d. C., el Almagesto.
El movimiento epicíclico se usa en el mecanismo de Antikythera, un antiguo dispositivo astronómico griego, para compensar la órbita elíptica de la Luna, moviéndose más rápido en el perigeo y más lento en el apogeo que las órbitas circulares, usando cuatro engranajes, dos de ellos engranados en una forma excéntrica que se aproxima bastante a la segunda ley de Kepler.
Los epiciclos funcionaron muy bien y fueron muy precisos porque, como mostró más tarde el análisis de Fourier, cualquier curva suave se puede aproximar a una precisión arbitraria con un número suficiente de epiciclos. Sin embargo, cayeron en desgracia con el descubrimiento de que los movimientos planetarios eran en gran medida elípticos desde un marco de referencia heliocéntrico, lo que llevó al descubrimiento de que la gravedad que obedece a una simple ley del inverso del cuadrado podría explicar mejor todos los movimientos planetarios.
Introducción
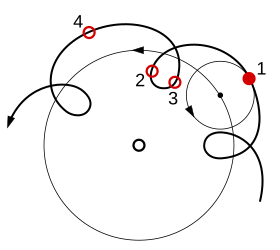
Tanto en el sistema hipparquiano como en el ptolemaico, se supone que los planetas se mueven en un círculo pequeño llamado epiciclo, que a su vez se mueve a lo largo de un círculo más grande llamado deferente. Ambos círculos giran en el sentido de las agujas del reloj y son aproximadamente paralelos al plano de la órbita aparente del Sol bajo esos sistemas (eclíptica). A pesar de que el sistema se considera geocéntrico, ninguno de los círculos era exactamente concéntrico con la Tierra. Más específicamente, el movimiento de cada planeta se centró en un punto específico del planeta ligeramente alejado de la Tierra llamado excéntrico. Las órbitas de los planetas en este sistema son similares a las epitrocoides.
En el sistema hipparquiano el epiciclo rotaba y giraba a lo largo del deferente con movimiento uniforme. Sin embargo, Ptolomeo descubrió que no podía conciliar eso con los datos de observación babilónicos disponibles para él; en particular, la forma y el tamaño de los retrógrados aparentes diferían. La velocidad angular a la que viajaba el epiciclo no era constante a menos que la midiera desde otro punto al que llamó ecuante. Era la velocidad angular a la que el deferente se movía alrededor del punto medio entre el ecuante y la Tierra (la excéntrica) lo que era constante; el centro del epiciclo barrió ángulos iguales en tiempos iguales solo cuando se ve desde el ecuante. Fue el uso de ecuantes para desacoplar el movimiento uniforme del centro de los deferentes circulares lo que distinguió el sistema ptolemaico.
Ptolomeo no predijo los tamaños relativos de los deferentes planetarios en el Almagest. Todos sus cálculos se realizaron con respecto a un deferente normalizado, considerando un solo caso a la vez. Esto no quiere decir que creyera que los planetas eran todos equidistantes, pero no tenía una base para medir distancias, excepto la Luna. Generalmente ordenaba los planetas hacia el exterior de la Tierra en función de sus períodos de órbita. Posteriormente calculó sus distancias en las Hipótesis Planetarias y las resumió en la primera columna de esta tabla:
| Cuerpo | Tamaño medio (en el radio terrestre) | Valor moderno (semimajor axis, in Earth radii) | Ratio (moderno/Ptolomeo) | Ratio (moderno/Ptolomeo, normalizado al Sol = 1) |
|---|---|---|---|---|
| Luna | 48 | 60.3 | 1.26 | 0,065 |
| Mercurio | 115 | 9,090 | 79.0 | 4.1 |
| Venus | 622,5 | 16.980 | 27.3 | 1.4 |
| Sol | 1.210 | 23.480 | 19.4 | 1 |
| Marte | 5,040 | 35.780 | 7.10 | 0.37 |
| Júpiter | 11,504 | 122.200 | 10.6 | 0,555 |
| Saturno | 17.026 | 225.000 | 13.2 | 0,688 |
| Concha de estrellas | 20.000 | — | — | — |
Si sus valores para los radios deferentes en relación con la distancia entre la Tierra y el Sol hubieran sido más precisos, todos los tamaños de los epiciclos se habrían aproximado a la distancia entre la Tierra y el Sol. Aunque todos los planetas se consideran por separado, todos estaban unidos de una manera peculiar: las líneas trazadas desde el cuerpo a través del centro epicéntrico de todos los planetas eran todas paralelas, junto con la línea trazada desde el Sol hasta la Tierra a lo largo de la cual Mercurio y Venus estaban situados. Eso significa que todos los cuerpos giran en sus epiciclos al mismo tiempo que el Sol de Ptolomeo (es decir, todos tienen exactamente un período de un año).
Las observaciones babilónicas mostraron que, en el caso de los planetas superiores, el planeta normalmente se movería en el cielo nocturno más lento que las estrellas. Cada noche, el planeta parecía retrasarse un poco con respecto a las estrellas, en lo que se denomina movimiento progresivo. Cerca de la oposición, el planeta parecería retroceder y moverse a través del cielo nocturno más rápido que las estrellas durante un tiempo en movimiento retrógrado antes de retroceder nuevamente y reanudar el progrado. La teoría epicíclica, en parte, buscó explicar este comportamiento.
Siempre se observó que los planetas inferiores estaban cerca del Sol, apareciendo solo poco antes del amanecer o poco después del atardecer. Su aparente movimiento retrógrado ocurre durante la transición entre la estrella de la tarde y la estrella de la mañana, cuando pasan entre la Tierra y el Sol.
Historia
Cuando los antiguos astrónomos observaban el cielo, veían el Sol, la Luna y las estrellas moviéndose sobre su cabeza de forma regular. Los babilonios hicieron observaciones celestiales, principalmente del sol y la luna como un medio para recalibrar y preservar el cronometraje de las ceremonias religiosas. Otras civilizaciones tempranas, como los griegos, tuvieron pensadores como Tales de Mileto, el primero en documentar y predecir un eclipse solar, o Heráclides, el primer astrónomo registrado en proponer un modelo geocéntrico para el cosmos. También vieron a los "vagabundos" o "planetai" (nuestros planetas). La regularidad en los movimientos de los cuerpos errantes sugirió que sus posiciones podrían ser predecibles.
El enfoque más obvio para el problema de predecir los movimientos de los cuerpos celestes era simplemente mapear sus posiciones contra el campo estelar y luego ajustar funciones matemáticas a las posiciones cambiantes. La introducción de mejores instrumentos de medición celeste, como la introducción del gnomon por parte de Anaximandro, permitió a los griegos comprender mejor el paso del tiempo, como el número de días del año y la duración de las estaciones, que son indispensables para mediciones astronómicas.
Los antiguos trabajaban desde una perspectiva geocéntrica por la sencilla razón de que la Tierra estaba donde ellos se paraban y observaban el cielo, y es el cielo el que parece moverse mientras que el suelo parece quieto y firme bajo los pies. Algunos astrónomos griegos (p. ej., Aristarco de Samos) especularon que los planetas (incluida la Tierra) giraban alrededor del Sol, pero la óptica (y las matemáticas específicas, la ley de la gravitación de Isaac Newton, por ejemplo) era necesaria para proporcionar datos que resultaran convincentes. apoyar el modelo heliocéntrico no existía en la época de Ptolomeo y no aparecería hasta más de mil quinientos años después de su época. Además, la física aristotélica no fue diseñada con este tipo de cálculos en mente, y la filosofía de Aristóteles con respecto a los cielos estaba totalmente en desacuerdo con el concepto de heliocentrismo. No fue hasta que Galileo Galilei observó las lunas de Júpiter el 7 de enero de 1610 y las fases de Venus en septiembre de 1610, que el modelo heliocéntrico comenzó a recibir un amplio apoyo entre los astrónomos, quienes también llegaron a aceptar la noción de que los planetas son mundos individuales. orbitando alrededor del Sol (es decir, que la Tierra también es un planeta). Johannes Kepler formuló sus tres leyes del movimiento planetario, que describen las órbitas de los planetas de nuestro sistema solar con un notable grado de precisión utilizando un sistema que emplea órbitas elípticas en lugar de circulares. Las tres leyes de Kepler todavía se enseñan hoy en las clases universitarias de física y astronomía, y la redacción de estas leyes no ha cambiado desde que Kepler las formuló por primera vez hace cuatrocientos años.
El movimiento aparente de los cuerpos celestes con respecto al tiempo es de naturaleza cíclica. Apolonio de Perge se dio cuenta de que esta variación cíclica podía representarse visualmente mediante pequeñas órbitas circulares, o epiciclos, que giraban en órbitas circulares más grandes, o deferentes. Hipparchus calculó las órbitas requeridas. Los deferentes y epiciclos en los modelos antiguos no representaban órbitas en el sentido moderno, sino un conjunto complejo de trayectorias circulares cuyos centros están separados por una distancia específica para aproximarse al movimiento observado de los cuerpos celestes.
Claudius Ptolomeo perfeccionó el concepto de deferente y epiciclo e introdujo el ecuante como un mecanismo que explica las variaciones de velocidad en los movimientos de los planetas. La metodología empírica que desarrolló demostró ser extraordinariamente precisa para su época y todavía estaba en uso en la época de Copérnico y Kepler. Es importante aclarar que un modelo heliocéntrico no es necesariamente más preciso como sistema para rastrear y predecir los movimientos de los cuerpos celestes que uno geocéntrico al considerar órbitas estrictamente circulares. Un sistema heliocéntrico requeriría sistemas más complejos para compensar el cambio en el punto de referencia. No fue hasta la propuesta de Kepler de órbitas elípticas que dicho sistema se volvió cada vez más preciso que un mero modelo geocéntrico epicíclico.
Owen Gingerich describe una conjunción planetaria que ocurrió en 1504 y aparentemente fue observada por Copérnico. En notas encuadernadas con su copia de las Tablas alfonsinas, Copérnico comentó que "Marte supera a los números en más de dos grados. Saturno es superado por los números en un grado y medio." Utilizando modernos programas informáticos, Gingerich descubrió que, en el momento de la conjunción, Saturno se encontraba realmente a la zaga de las tablas en un grado y medio y Marte aventajaba las predicciones en casi dos grados. Además, descubrió que las predicciones de Ptolomeo para Júpiter al mismo tiempo eran bastante precisas. Por lo tanto, Copérnico y sus contemporáneos usaban los métodos de Ptolomeo y los encontraban dignos de confianza mucho más de mil años después de que se publicara el trabajo original de Ptolomeo.
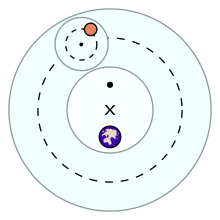
Cuando Copérnico transformó las observaciones terrestres en coordenadas heliocéntricas, se enfrentó a un problema completamente nuevo. Las posiciones centradas en el Sol mostraban un movimiento cíclico con respecto al tiempo pero sin bucles retrógrados en el caso de los planetas exteriores. En principio, el movimiento heliocéntrico era más simple pero con nuevas sutilezas debido a la forma elíptica aún por descubrir de las órbitas. Otra complicación fue causada por un problema que Copérnico nunca resolvió: dar cuenta correctamente del movimiento de la Tierra en la transformación de coordenadas. De acuerdo con la práctica anterior, Copérnico usó el modelo deferente/epiciclo en su teoría, pero sus epiciclos eran pequeños y se llamaban 'epiciclos'.
En el sistema ptolemaico los modelos para cada uno de los planetas eran diferentes, y así fue con Copérnico' modelos iniciales. Sin embargo, mientras trabajaba con las matemáticas, Copérnico descubrió que sus modelos podían combinarse en un sistema unificado. Además, si se escalaran de modo que la órbita de la Tierra fuera la misma en todos ellos, el orden de los planetas que reconocemos hoy se seguiría fácilmente a partir de las matemáticas. Mercurio orbitaba más cerca del Sol y el resto de los planetas ocupaban su lugar en orden hacia afuera, ordenados en distancia por sus períodos de revolución.
Aunque Copérnico' Los modelos redujeron considerablemente la magnitud de los epiciclos, si eran más simples que los de Ptolomeo es discutible. Copérnico eliminó el ecuante algo difamado de Ptolomeo, pero a costa de epiciclos adicionales. Varios libros del siglo XVI basados en Ptolomeo y Copérnico usan aproximadamente la misma cantidad de epiciclos. La idea de que Copérnico usó solo 34 círculos en su sistema proviene de su propia declaración en un boceto preliminar no publicado llamado Commentariolus. Cuando publicó De revolutionibus orbium coelestium, había añadido más círculos. Contar el número total es difícil, pero se estima que creó un sistema igual de complicado, o incluso más. Koestler, en su historia de la visión humana del universo, iguala el número de epiciclos utilizados por Copérnico en 48. El total popular de unos 80 círculos para el sistema ptolemaico parece haber aparecido en 1898. Puede haber sido inspirado por el sistema no ptolemaico de Girolamo Fracastoro, que utilizó 77 o 79 orbes en su sistema inspirado en Eudoxo de Cnido. Copérnico en sus obras exageró el número de epiciclos utilizados en el sistema ptolemaico; aunque los conteos originales oscilaban en 80 círculos, en la época de Copérnico, Peurbach había actualizado el sistema ptolemaico hacia un número similar de 40; por lo tanto, Copérnico reemplazó efectivamente el problema de la retrógrada con más epiciclos.
Copérnico' La teoría era al menos tan precisa como la de Ptolomeo, pero nunca alcanzó la estatura y el reconocimiento de la teoría de Ptolomeo. Lo que se necesitaba era la teoría de la órbita elíptica de Kepler, que no se publicó hasta 1609 y 1619. Copérnico El trabajo proporcionó explicaciones para fenómenos como el movimiento retrógrado, pero en realidad no probó que los planetas realmente orbitaran alrededor del Sol.
Ptolomeo y Copérnico Las teorías demostraron la durabilidad y adaptabilidad del dispositivo deferente/epiciclo para representar el movimiento planetario. Los modelos deferente/epiciclo funcionaron tan bien debido a la extraordinaria estabilidad orbital del sistema solar. Cualquiera de las teorías podría usarse hoy si Gottfried Wilhelm Leibniz e Isaac Newton no hubieran inventado el cálculo.
Según Maimónides, el ahora perdido sistema astronómico de Ibn Bajjah en la España andaluza del siglo XII carecía de epiciclos. Gersonides de la Francia del siglo XIV también eliminó los epiciclos, argumentando que no se alineaban con sus observaciones. A pesar de estos modelos alternativos, los epiciclos no se eliminaron por completo hasta el siglo XVII, cuando el modelo de órbitas elípticas de Johannes Kepler reemplazó gradualmente al de Copérnico. modelo basado en círculos perfectos.
La mecánica newtoniana o clásica eliminó por completo la necesidad de métodos deferentes/epiciclos y produjo teorías más precisas. Al tratar al Sol y a los planetas como masas puntuales y al utilizar la ley de gravitación universal de Newton, se derivaron ecuaciones de movimiento que podían resolverse por varios medios para calcular predicciones de velocidades y posiciones orbitales planetarias. Si se aproximaran como problemas simples de dos cuerpos, por ejemplo, podrían resolverse analíticamente, mientras que el problema más realista de n cuerpos requería métodos numéricos para su solución.
El descubrimiento de Neptuno ilustra el poder de la mecánica newtoniana para resolver problemas de mecánica orbital. El análisis de las perturbaciones observadas en la órbita de Urano produjo estimaciones de la posición del presunto planeta dentro de un grado de donde se encontró. Esto no podría haberse logrado con métodos deferentes/epiciclo. Aún así, Newton en 1702 publicó la Teoría del movimiento de la luna que empleó un epiciclo y se mantuvo en uso en China hasta el siglo XIX. Las tablas posteriores basadas en la Teoría de Newton podrían haberse acercado a la precisión del minuto de arco.
El número de epiciclos
Según una escuela de pensamiento en la historia de la astronomía, las imperfecciones menores en el sistema ptolemaico original se descubrieron mediante observaciones acumuladas a lo largo del tiempo. Se creyó erróneamente que se agregaron más niveles de epiciclos (círculos dentro de círculos) a los modelos para que coincidieran con mayor precisión con los movimientos planetarios observados. Se cree que la multiplicación de epiciclos condujo a un sistema casi impracticable en el siglo XVI, y que Copérnico creó su sistema heliocéntrico para simplificar la astronomía ptolemaica de su época, logrando así reducir drásticamente el número de círculos.
Con mejores observaciones se utilizaron epiciclos y excéntricos adicionales para representar los fenómenos recién observados hasta que en la Edad Media posterior el universo se convirtió en una 'Esfera/Con Centric y Eccentric scribbled o'er,/Cículo y Epiciclo, Orb en Orb'.
—Dorothy Stimson, La aceptación gradual de la Teoría Copérnica del Universo, 1917
Como medida de complejidad, el número de círculos es de 80 para Ptolomeo, frente a los 34 de Copérnico. El número más alto apareció en la Encyclopædia Britannica sobre astronomía durante la década de 1960, en una discusión sobre el interés del rey Alfonso X de Castilla por la astronomía durante el siglo XIII. (A Alfonso se le atribuye el encargo de las Tablas Alfonsinas).
En este momento cada planeta había sido proporcionado de 40 a 60 epiciclos para representar después de una moda su complejo movimiento entre las estrellas. Sorprendido por la dificultad del proyecto, Alfonso se acredita con la observación de que si hubiera estado presente en la Creación podría haber dado excelentes consejos.
—Encyclopædia Britannica, 1968
Resulta que una de las principales dificultades de esta teoría de epiciclos sobre epiciclos es que los historiadores que examinan libros sobre astronomía ptolemaica de la Edad Media y el Renacimiento no han encontrado absolutamente ningún rastro del uso de múltiples epiciclos para cada planeta. Las tablas alfonsinas, por ejemplo, aparentemente se calcularon utilizando los métodos originales sin adornos de Ptolomeo.
Otro problema es que los propios modelos desaconsejaban los retoques. En un modelo de deferente y epiciclo, las partes del todo están interrelacionadas. Un cambio en un parámetro para mejorar el ajuste en un lugar desequilibraría el ajuste en otro lugar. El modelo de Ptolomeo es probablemente óptimo en este sentido. En general, dio buenos resultados, pero falló un poco aquí y allá. Los astrónomos experimentados habrían reconocido estas deficiencias y las habrían tenido en cuenta.
Formalismo matemático
Según el historiador de la ciencia Norwood Russell Hanson:
No existe una curva bilateral-simétrica, ni eccentrísticamente-periodica utilizada en ninguna rama de astrofísica o astronomía observacional que no podría ser trazada suavemente como el movimiento resultante de un punto girando dentro de una constelación de epiciclos, finita en número, girando alrededor de un deferente fijo.
—Norwood Russell Hanson, "El Poder Matemático de la Astronomía Epicíclica", 1960
Cualquier camino, periódico o no, cerrado o abierto, puede representarse con un número infinito de epiciclos. Esto se debe a que los epiciclos se pueden representar como una serie compleja de Fourier; por lo tanto, con una gran cantidad de epiciclos, se pueden representar caminos muy complejos en el plano complejo.
Sea el número complejo
donde a0 y k< sub>0 son constantes, i = √−1 es la unidad imaginaria, y t es el tiempo, corresponden a un deferente centrado en el origen del plano complejo y que gira con un radio a0 y angular velocidad
donde T es el punto.
Si z1 es la ruta de un epiciclo, entonces el epiciclo deferente más se representa como la suma
Esta es una función casi periódica, y es una función periódica justo cuando la relación de las constantes kj es racional La generalización a N epiciclos produce la función casi periódica
que es periódico justo cuando cada par de kj está racionalmente relacionado. Encontrar los coeficientes aj para representar una ruta dependiente del tiempo en el plano complejo, z = f(t), es el objetivo de reproducir una órbita con deferentes y epiciclos, y esta es una manera de "salvar los fenómenos" (σώζειν τα φαινόμενα).
Este paralelo fue observado por Giovanni Schiaparelli. Pertinente al debate de la Revolución Copernicana sobre "salvar los fenómenos" versus ofrecer explicaciones, uno puede entender por qué Tomás de Aquino, en el siglo XIII, escribió:
La razón puede ser empleada de dos maneras para establecer un punto: primero, con el propósito de proporcionar suficiente prueba de algún principio [...]. La razón se emplea de otra manera, no como proporcionar una prueba suficiente de un principio, sino como confirmar un principio ya establecido, al mostrar la congruencia de sus resultados, como en la astronomía la teoría de los excéntricos y los epiciclos se considera como establecido, porque así se pueden explicar las apariencias sensibles de los movimientos celestiales; no, sin embargo, como si esta prueba fuera suficiente, ya que alguna otra teoría podría explicarlos.
—Tomás de Aquino, Summa Theologica
Epiciclos y la Iglesia Católica
Siendo un sistema que se utilizó en su mayor parte para justificar el modelo geocéntrico, con la excepción de Copérnico' cosmos, se favoreció el modelo deferente y epiciclo sobre las ideas heliocéntricas que propusieron Kepler y Galileo. La iglesia apoyó este modelo porque favorecía su dogma central. Los adoptantes posteriores del modelo epicíclico, como Tycho Brahe, que tuvo en cuenta las escrituras de la Iglesia al crear su modelo, fueron vistos incluso de forma más favorable. El modelo de Tychonic era un modelo híbrido que combinaba las características geocéntricas y heliocéntricas, con una Tierra inmóvil rodeada por el sol y la luna, y los planetas girando alrededor del sol. Para Brahe, la idea de una Tierra que gira y se mueve era imposible, y las escrituras deberían ser siempre primordiales y respetadas. Cuando Galileo trató de desafiar el sistema de Tycho Brahe, la iglesia no estaba satisfecha con el desafío de sus puntos de vista. La publicación de Galileo no ayudó a su caso en su juicio.
Mala ciencia
"Agregar epiciclos" ha llegado a ser utilizado como un comentario despectivo en la discusión científica moderna. El término podría usarse, por ejemplo, para describir el intento continuo de ajustar una teoría para hacer que sus predicciones coincidan con los hechos. Existe una idea generalmente aceptada de que se inventaron epiciclos adicionales para aliviar los crecientes errores que el sistema ptolemaico notaba a medida que las mediciones se volvían más precisas, particularmente para Marte. Según esta noción, los epiciclos son considerados por algunos como el ejemplo paradigmático de la mala ciencia.
Copérnico agregó un epiciclo adicional a sus planetas, pero eso fue solo en un esfuerzo por eliminar el ecuante de Ptolomeo, que consideró una ruptura filosófica con la perfección de los cielos de Aristóteles. Matemáticamente, el segundo epiciclo y el ecuante producen los mismos resultados, y muchos astrónomos copernicanos antes de Kepler continuaron usando el ecuante, ya que los cálculos matemáticos eran más fáciles. Copérnico' Los epiciclos también eran mucho más pequeños que los de Ptolomeo y eran necesarios porque los planetas de su modelo se movían en círculos perfectos. Johannes Kepler demostraría más tarde que los planetas se mueven en elipses, lo que eliminó la necesidad de la teoría de Copérnico. también epiciclos.
Contenido relacionado
Principio copernicano
Inclinación axial
Impulso específico