Decágono

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Forma con diez lados

En geometría, un decágono (del griego δέκα déka y γωνία gonía, "diez ángulos") es un polígono de diez lados o 10-gon. La suma total de los ángulos interiores de un decágono simple es 1440°.

Decágono normal

Un decágono regular tiene todos los lados de igual longitud y cada ángulo interno siempre será igual a 144°. Su símbolo de Schläfli es {10} y también se puede construir como un pentágono truncado, t{5}, un decágono casi regular que alterna dos tipos de aristas.

Largo del lado

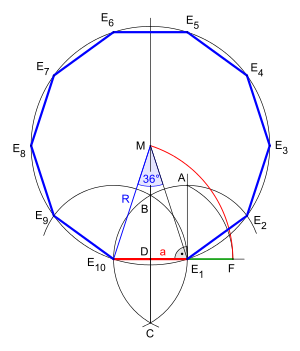
La imagen muestra un decagon regular con longitud lateral $a$ y radio $R$ del círculo circunscrito.

El triángulo ${displaystyle E_{10}E_{1}M}$ tiene dos piernas igualmente largas con longitud $R$ y una base con longitud $a$
El círculo alrededor $E_{1}$ con radio $a$ intersects ${displaystyle ]M,E_{10}[}$ en un punto $P$ (no designado en la imagen).
Ahora el triángulo ${displaystyle {E_{10}E_{1}P};}$ es un triángulo isosceles con vértice $E_{1}$ y con ángulos de base ${displaystyle mangle E_{1}E_{10}P=mangle E_{10}PE_{1}=72^{circ };}$ .
Por lo tanto ${displaystyle mangle PE_{1}E_{10}=180^{circ }-2cdot 72^{circ }=36^{circ };}$ . Así que... ${displaystyle ;mangle ME_{1}P=72^{circ }-36^{circ }=36^{circ };}$ y por consiguiente ${displaystyle ;E_{1}MP;}$ es también un triángulo isosceles con vértice $P$ . La longitud de sus piernas es $a$ , así la longitud ${displaystyle [P,E_{10}]}$ es ${displaystyle R-a}$ .
Los triángulos isosceles ${displaystyle E_{10}E_{1}M;}$ y ${displaystyle PE_{10}E_{1};}$ tienen ángulos iguales de 36° en el vértice, y por lo tanto son similares, por lo tanto: ${displaystyle ;{frac {a}{R}}={frac {R-a}{a}}}$
Multiplicación con los denominadores $0}" xmlns="http://www.w3.org/1998/Math/MathML">R,a■0{displaystyle R,a confía0}0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/de6e7633056dcb73ed1dad867b1bd614ba93141f" style="vertical-align: -0.671ex; width:8.289ex; height:2.509ex;"/>$ conduce a la ecuación cuadrática: ${displaystyle ;a^{2}=R^{2}-aR;}$
Esta ecuación para la longitud lateral $a,$ tiene una solución positiva: ${displaystyle ;a={frac {R}{2}}(-1+{sqrt {5}})}$

Did you mean:

So the regular decagon can be constructed with ruler and compass.

Conclusiones adicionales

${displaystyle ;R={frac {2a}{{sqrt {5}}-1}}={frac {a}{2}}({sqrt {5}}+1);}$ y la altura base de ${displaystyle Delta ,E_{10}E_{1}M,}$ (es decir, la longitud ${displaystyle [M,D]}$ ) es ${displaystyle h={sqrt {R^{2}-(a/2)^{2}}}={frac {a}{2}}{sqrt {5+2{sqrt {5}}}};}$ y el triángulo tiene el área: ${displaystyle A_{Delta }={frac {a}{2}}cdot h={frac {a^{2}}{4}}{sqrt {5+2{sqrt {5}}}}}$ .

Área

El área de un decágono regular de lado a viene dada por:

{displaystyle A={frac {5}{2}}a^{2}cot left({frac {pi }{10}}right)={frac {5}{2}}a^{2}{sqrt {5+2{sqrt {5}}}}simeq 7.694208843,a^{2}}

En términos de la apotema r (ver también figura inscrita), el área es:

{displaystyle A=10tan left({frac {pi }{10}}right)r^{2}=2r^{2}{sqrt {5left(5-2{sqrt {5}}right)}}simeq 3.249196962,r^{2}}

En términos del circunradio R, el área es:

{displaystyle A=5sin left({frac {pi }{5}}right)R^{2}={frac {5}{2}}R^{2}{sqrt {frac {5-{sqrt {5}}}{2}}}simeq 2.938926261,R^{2}}

Una fórmula alternativa es ${displaystyle A=2.5da}$ Donde d es la distancia entre los lados paralelos, o la altura cuando el decagón permanece en un lado como base, o el diámetro del círculo inscrito del decagón. Por simple trigonometría,

{displaystyle d=2aleft(cos {tfrac {3pi }{10}}+cos {tfrac {pi }{10}}right),}

y se puede escribir algebraicamente como

{displaystyle d=a{sqrt {5+2{sqrt {5}}}}.}

Lados

Un decágono regular tiene 10 lados y es equilátero. tiene 35 diagonales

Construcción

Como 10 = 2 × 5, una potencia de dos veces un primo de Fermat, se deduce que se puede construir un decágono regular usando compás y regla, o mediante una bisección de borde de un pentágono regular.

Construcción de decagón

Construcción del Pentágono

Un método alternativo (pero similar) es el siguiente:

Construir un pentágono en un círculo por uno de los métodos mostrados en la construcción de un pentágono.
Extender una línea de cada vértice del Pentágono a través del centro del círculo al lado opuesto de ese mismo círculo. Donde cada línea corta el círculo es un vértice del decagón. En otras palabras, la imagen de un pentágono regular bajo un punto de reflexión con respecto a su centro es un concéntrico congruentePentágono, y los dos pentágonos tienen en total los vértices de un concéntrico regular decagon.
Los cinco ángulos del Pentágono constituyen rincones alternativos del decagón. Únete a estos puntos a los nuevos puntos adyacentes para formar el decagón.

Did you mean:

Non Convex regular decagon

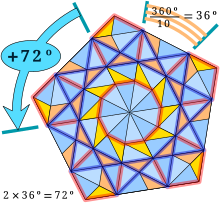
La relación longitudinal de dos bordes inigualables de un triángulo dorado es la relación dorada, denotada por $Phi$ , o su inverso multiplicativo:

{displaystyle Phi -1={frac {1}{Phi }}=2,cos 72,^{circ }={frac {1}{,2,cos 36,^{circ }}}={frac {,{sqrt {5}}-1,}{2}}{text{.}}}

La proporción áurea en decágono

Tanto en la construcción con un circuncírculo dado como con una longitud de lado dada, la proporción áurea que divide un segmento de línea por la división exterior es el elemento constructivo determinante.

En la construcción con circuncirco dado el arco circular alrededor G con radio GE₃ produce el segmento AH, cuya división corresponde a la relación de oro.

{displaystyle {frac {overline {AM}}{overline {MH}}}={frac {overline {AH}}{overline {AM}}}={frac {1+{sqrt {5}}}{2}}=Phi approx 1.618{text{.}}}

En la construcción con longitud lateral dada el arco circular alrededor de D con radio DA produce el segmento E₁₀F, cuya división corresponde a la relación de oro.

{displaystyle {frac {overline {E_{1}E_{10}}}{overline {E_{1}F}}}={frac {overline {E_{10}F}}{overline {E_{1}E_{10}}}}={frac {R}{a}}={frac {1+{sqrt {5}}}{2}}=Phi approx 1.618{text{.}}}

Decagon con circuncirco dado, animación

Decagon con una longitud lateral dada, animación

Simetría

El decágono regular tiene simetría Dih10, orden 20. Hay 3 simetrías diédricas de subgrupos: Dih₅, Dih₂ y Dih₁ y 4 simetrías de grupos cíclicos: Z₁₀, Z₅, Z₂ y Z₁.

Estas 8 simetrías se pueden ver en 10 simetrías distintas en el decágono, un número mayor porque las líneas de reflexión pueden pasar a través de vértices o bordes. John Conway los etiqueta con una letra y un orden de grupo. La simetría completa de la forma regular es r20 y ninguna simetría está etiquetada como a1. Las simetrías diédricas se dividen según pasen por vértices (d para diagonal) o aristas (p para perpendiculares), y i cuando la reflexión trayectoria de las líneas a través de ambos bordes y vértices. Las simetrías cíclicas en la columna del medio están etiquetadas como g para sus órdenes de giro central.

Cada simetría de subgrupo permite uno o más grados de libertad para formas irregulares. Solo el subgrupo g10 no tiene grados de libertad pero puede verse como aristas dirigidas.

Los decágonos irregulares de mayor simetría son d10, un decágono isogonal construido por cinco espejos que pueden alternar bordes largos y cortos, y p10, un decágono isotoxal, construido con igual longitudes de arista, pero vértices que alternan dos ángulos internos diferentes. Estas dos formas son duales entre sí y tienen la mitad del orden de simetría del decágono regular.

Disección

Proyección de 10 cachorros	40 romb disección

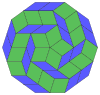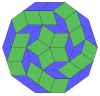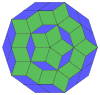
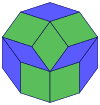
Coxeter afirma que cada zonogon (un 2m-gon cuyos lados opuestos son paralelos y de igual longitud) se puede dividir en m(m-1)/2 paralelogramos. En particular, esto es cierto para polígonos regulares con muchos lados iguales, en cuyo caso los paralelogramos son todos rombos. Para el decágono regular, m=5, y se puede dividir en 10 rombos, con los ejemplos que se muestran a continuación. Esta descomposición se puede ver como 10 de 80 caras en un plano de proyección del polígono de Petrie del cubo de 5. Una disección se basa en 10 de 30 caras del triacontaedro rómbico. La lista OEIS: A006245 define el número de soluciones como 62, con 2 orientaciones para la primera forma simétrica y 10 orientaciones para las otras 6.

Decagon regular diseccionado en 10 rhombi
5-cube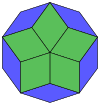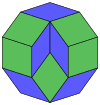

Decágono sesgado

3 decagones skew zig-zag regular
{5} {}}	{5/2}	{5/3} {}}}

Un decágono skew regular se ve como bordes zig-zagging de un antiprisma pentagonal, un antiprismo pentagramamico, y un pentagramamic cruzado-antiprismo.

Un decágono sesgado es un polígono sesgado con 10 vértices y aristas pero que no existe en el mismo plano. El interior de tal decágono generalmente no está definido. Un decágono en zig-zag sesgado tiene vértices que se alternan entre dos planos paralelos.

Un decágono sesgado regular es de vértice transitivo con longitudes de borde iguales. En 3 dimensiones será un decágono sesgado en zig-zag y se puede ver en los vértices y bordes laterales de un antiprisma pentagonal, antiprisma pentagrammico y antiprisma cruzado pentagrammico con el mismo D_5d, [ 2⁺,10] simetría, orden 20.

Estos también se pueden ver en estos 4 poliedros convexos con simetría icosaédrica. Los polígonos en el perímetro de estas proyecciones son decágonos oblicuos regulares.

Proyecciones ortogonales de polihedra en ejes 5
Dodecahedron	Icosahedron	Icosidodecahedron	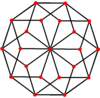Triacontahedron Rhombic

Polígonos de Petrie

El decágono sesgado regular es el polígono de Petrie para muchos politopos de dimensiones superiores, que se muestra en estas proyecciones ortogonales en varios planos de Coxeter: El número de lados en el polígono de Petrie es igual al número de Coxeter, h, para cada familia de simetría.

A₉	D₆		B₅
9-simplex	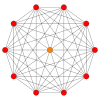411	131	5-orthoplex	5-cube

Contenido relacionado

Más resultados...