De cadena

La ecuación de Whewell para la catenaria es

$${displaystyle tan varphi ={frac {} {}}}$$

${displaystyle varphi }$

La diferenciación da

$${fnMicrosoft {fnMicrosoft {fnMicrosoft {\fnMicrosoft {\fnMicrosoft {\fnMicrosoft {\\fnMicrosoft {\\\fn\\\\fnMicrosoft {\\\fnMicrosoft {\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ } {ds}={frac {cos ^{2}varphi } {}} {c}}$$

${displaystyle varphi }$

$${displaystyle kappa ={frac {a}{2}+a}}}}}$$

${displaystyle kappa }$

El radio de curvatura es entonces

$${displaystyle rho =asec ^{2}varphi}$$

Relación con otras curvas

Cuando se hace rodar una parábola en línea recta, la curva de la ruleta trazada por su foco es una catenaria. La envolvente de la directriz de la parábola también es una catenaria. La involuta del vértice, es decir, la ruleta trazada por un punto que parte del vértice cuando se rueda una línea sobre una catenaria, es la tractriz.

Otra ruleta, formada al hacer rodar una línea en una catenaria, es otra línea. Esto implica que las ruedas cuadradas pueden rodar perfectamente sobre una carretera formada por una serie de baches en forma de catenaria invertida. Las ruedas pueden ser cualquier polígono regular excepto un triángulo, pero la catenaria debe tener parámetros correspondientes a la forma y dimensiones de las ruedas.

Propiedades geométricas

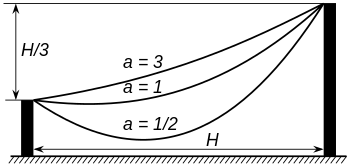
En cualquier intervalo horizontal, la relación entre el área bajo la catenaria y su longitud es igual a a, independientemente del intervalo seleccionado. La catenaria es la única curva plana distinta de una línea horizontal con esta propiedad. Además, el centroide geométrico del área bajo un tramo de catenaria es el punto medio del segmento perpendicular que conecta el centroide de la curva misma y la x< /span>-eje.

Ciencia

Una carga en movimiento en un campo eléctrico uniforme viaja a lo largo de una catenaria (que tiende a una parábola si la velocidad de la carga es mucho menor que la velocidad de la luz c).

La superficie de revolución con radios fijos en cada extremo que tiene un área de superficie mínima es una catenaria girada alrededor del eje x.

Análisis

Modelo de cadenas y arcos

En el modelo matemático, la cadena (o cordón, cable, soga, cordel, etc.) se idealiza asumiendo que es tan delgada que puede considerarse como una curva y que es tan flexible que cualquier fuerza de tensión ejercida por la cadena es paralelo a la cadena. El análisis de la curva para un arco óptimo es similar excepto que las fuerzas de tensión se convierten en fuerzas de compresión y todo se invierte. Un principio subyacente es que la cadena puede considerarse un cuerpo rígido una vez que ha alcanzado el equilibrio. Las ecuaciones que definen la forma de la curva y la tensión de la cadena en cada punto pueden obtenerse mediante una inspección cuidadosa de las diversas fuerzas que actúan sobre un segmento, teniendo en cuenta que estas fuerzas deben estar en equilibrio si la cadena está en equilibrio estático.

Deje que el camino seguido por la cadena esté dado paramétricamente por r = (x, y) = (x(s), y(s)) donde s representa la longitud del arco y r es el vector de posición. Esta es la parametrización natural y tiene la propiedad de que

$${displaystyle {frac {dmathbf} } {ds}= mathbf {u}$$

donde u es un vector unitario tangente.

Diagrama de fuerzas que actúan en un segmento de un catenario c a r. Las fuerzas son la tensión T₀ a c, la tensión T a r, y el peso de la cadena (0, −λgs). Puesto que la cadena está en reposo la suma de estas fuerzas debe ser cero.

Se puede derivar una ecuación diferencial para la curva de la siguiente manera. Sea c el punto más bajo de la cadena, llamado vértice de la catenaria. La pendiente dy/dx de la curva es cero en c ya que es un punto mínimo. Supongamos que r está a la derecha de c ya que en el otro caso está implícito en la simetría. Las fuerzas que actúan sobre la sección de la cadena desde c hasta r son la tensión de la cadena en c, la tensión de la cadena en r y el peso de la cadena. La tensión en c es tangente a la curva en c y es por lo tanto horizontal sin ningún componente vertical y tira de la sección hacia la izquierda por lo que puede escribirse (−T₀, 0)< /span> donde T₀ es la magnitud de la fuerza. La tensión en r es paralela a la curva en r y tira de la sección a la derecha. La tensión en r se puede dividir en dos componentes, por lo que se puede escribir T u = (T cos φ, T sen φ), donde T es la magnitud de la fuerza y φ es el ángulo entre la curva en r y el x-eje (ver ángulo tangencial). Finalmente, el peso de la cadena está representado por (0, −λgs) donde λ es la masa por unidad de longitud, g es la intensidad del campo gravitacional y s es la longitud del segmento de cadena entre c y r.

La cadena está en equilibrio, por lo que la suma de las tres fuerzas es 0, por lo tanto

$${displaystyle Tcos varphi =T_{0}$$

$${displaystyle Tsin varphi =lambda gs,}$$

y dividir estos da

$${displaystyle {frac {}{dx}=tan varphi ={frac {lambda.$$

Es conveniente escribir

$${displaystyle a={frac {0}{lambda g}} {f}} {fnK}} {fn}}} {fn}}}} {fn}}}} {fnK}}}}}}$$

que es la longitud de la cadena cuyo peso es igual en magnitud a la tensión en c. Después

$${displaystyle {frac {fnMicroc} {fnMicroc} {fnMicrosoft} {fnMicrosoft} {fn}}} {fnMicrosoft}}}}} {fnMicroc}}}} {fnMicroc} {} {}}}}$$

es una ecuación que define la curva.

La componente horizontal de la tensión, T cos φ = T₀ es constante y la componente vertical de la tensión, T sin φ = λgs es proporcional a la longitud de la cadena entre r y el vértice.

Derivación de ecuaciones para la curva

La ecuación diferencial dada arriba se puede resolver para producir ecuaciones para la curva.

Desde

$${displaystyle {frac {fnMicroc} {fnMicroc} {fnMicrosoft} {fnMicrosoft} {fn}}} {fnMicrosoft}}}}} {fnMicroc}}}} {fnMicroc} {fn},}$$

la fórmula para la longitud del arco da

$${displaystyle {frac {dx}}={sqrt {1+left({dfrac {y}{dx}}}right)}={2}}={frac}={frac} {fnMicrosoft Sans Serif}$$

Entonces

$${displaystyle {frac {dx}{ds}={frac} {1}{frac} {ds}{dx}={frac {a}{sqrt {}}}}$$

y

$${displaystyle {frac {}{ds}={frac} {fnMicroc {} {fnMicroc} {fnMicroc}} {fnMicroc}} {f}} {fnMicroc}}} {fnMicroc}}}} {fnMicroc}}} {fnMicroc}}} {fnMicroc} {ds}{dx}={frac {fnMicrosoft Sans Serif} {fnMicrosoft} {fnMicrosoft} {fnMicrosoft} {f}} {fnMicrosoft} {fnMicrosoft}}} {fnMicrosoft}} {f}}}}} {f}}}}}}}} {f}fnf}f}f}}}f}}f}fnfnMisqt}}}}sqt}}}sqt}}}}sqtsqtsqt}}}}}}}} {f}}}}}}}}}}}}sqrt ¿Qué?$$

La segunda de estas ecuaciones se puede integrar para dar

$${displaystyle y={sqrt {a^{2}+s}+beta }$$

y cambiando la posición del eje x, β puede tomarse como 0. Entonces

$${displaystyle y={sqrt - ¿Qué?$$

El eje x así elegido se denomina directriz de la catenaria.

Se sigue que la magnitud de la tensión en un punto (x, y) es T = λgy, que es proporcional a la distancia entre el punto y la directriz.

Esta tensión también puede expresarse como T = T₀ y/a.

La integral de la expresión para dx/ds se puede encontrar usando técnicas estándar, dando

$${displaystyle x=aoperatorname {arsinh} left({frac {s}{a}right)+alpha ,}$$

y, de nuevo, cambiando la posición del eje y, α se puede tomar como 0. Entonces

$${displaystyle x=aoperatorname {arsinh} left({frac {s}{a}right),quad s=asinh left({frac {x}{a}right),}}right),}$$

El eje y así elegido pasa por el vértice y se denomina eje de la catenaria.

Estos resultados se pueden usar para eliminar s dando

$${displaystyle y=acosh left({frac {x}{a}right),}$$

Derivación alternativa

La ecuación diferencial se puede resolver usando un enfoque diferente. Desde

$${displaystyle s=atan varphi }$$

se deduce que

$${displaystyle {frac {dx}{dvarphi {fnMicroc {dx} {fnMicroc} {dvarphis} }=cos varphi cdot asec ^{2}varphi =asec varphi }$$

$${displaystyle {frac {y}{dvarphi} }={frac {y} {ds}{frac} {d}{dvarphi }=sin varphi cdot asec ^{2}varphi =atan varphi sec varphi varphi ,}$$

La integración da,

$${displaystyle x=aln(sec varphi +tan varphi)+alpha }$$

$${displaystyle y=asec varphi +beta ,}$$

Como antes, x y y se pueden desplazar para que α y β puede tomarse como 0. Entonces

$${displaystyle sec varphi +tan varphi =e^{frac {x}},}$$

$${displaystyle sec varphi -tan varphi =e^{-{frac.$$

Sumar y restar las dos últimas ecuaciones da la solución

$${displaystyle y=asec varphi =acosh left({frac {x}{a}right),}$$

$${displaystyle s=atan varphi =asinh left({frac {x}{a}right),}$$

Determinación de parámetros

Tres catenarios a través de los mismos dos puntos, dependiendo de la fuerza horizontal T_H.

En general, el parámetro a es la posición del eje. La ecuación se puede determinar en este caso de la siguiente manera:

${displaystyle lambda }$

${displaystyle x}$

$${fnMicroc {\fnMicrosoft {fnMicrosoft Sans Serif} {L}}{partial} {fnMicrosoft}}} {fnMicrosoft}}} {f}}} {f}}}} {fn}}}} {fnMicrosoft}}}}}}}} {f}}}}}}}} { - Sí.$$

${displaystyle C}$

$${displaystyle {frac {}}=-C}$$

Esta es una ecuación diferencial ordinaria de primer orden que se puede resolver por el método de separación de variables. Su solución es el coseno hiperbólico habitual donde los parámetros se obtienen a partir de las restricciones.

Generalizaciones con fuerza vertical

Cadenas no uniformes

Si la densidad de la cadena es variable, entonces el análisis anterior se puede adaptar para producir ecuaciones para la curva dada la densidad, o dada la curva para encontrar la densidad.

Sea w el peso por unidad de longitud de la cadena, entonces el peso de la cadena tiene una magnitud

$${displaystyle int _{mathbf {c} }{mathbf {r} }w,ds,}$$

donde los límites de integración son c y r. Equilibrio de fuerzas como en la cadena uniforme produce

$${displaystyle Tcos varphi =T_{0}$$

$${displaystyle Tsin varphi =int _{mathbf {c} }{mathbf {r} }w,ds,}$$

$${displaystyle {frac {fnK}=tan} varphi ={frac {1}{0}int _{mathbf {c} }{mathbf {r} }w,ds,.}$$

La diferenciación entonces da

$${displaystyle w=T_{0}{frac {d}{ds}{frac {y} {dx}={frac} {T_{0}{dfrac} {fnK} {fnMicroc {fnMicroc {fnMicroc {}fnMicroc}}}derecha)}}}},}}fnMicroc {fnMicroc} {fnMicroc}}}}}}}}}}}$$

En términos de φ y el radio de curvatura ρ esto se convierte en

$${displaystyle w={frac {T_{0}{rho cos ^{2}varphi },}$$

Curva puente colgante

Golden Gate Bridge. La mayoría de los cables de puente de suspensión siguen un parabólico, no una curva catenaria, porque la carretera es mucho más pesada que el cable.

Se puede realizar un análisis similar para encontrar la curva que sigue el cable que soporta un puente colgante con una calzada horizontal. Si el peso de la calzada por unidad de longitud es w y el peso del cable y el alambre que soportan el puente es insignificante en comparación, luego el peso sobre el cable (ver figura en Catenaria#Modelo de cadenas y arcos) desde c hasta r es wx donde x es la distancia horizontal entre c y r . Procediendo como antes se obtiene la ecuación diferencial

$${displaystyle {frac {}{dx}=tan varphi ={frac x,$$

Esto se resuelve mediante una integración simple para obtener

$${displaystyle y={frac {fnMicrosoft Sans Serif} }$$

y así el cable sigue una parábola. Si el peso del cable y los alambres de soporte no es despreciable, el análisis es más complejo.

Catenaria de igual fuerza

En una catenaria de igual resistencia, el cable se refuerza según la magnitud de la tensión en cada punto, por lo que su resistencia a la rotura es constante en toda su longitud. Suponiendo que la fuerza del cable es proporcional a su densidad por unidad de longitud, el peso, w, por unidad de longitud de la cadena se puede escribir T< span class="sr-only">/c, donde c es constante y se puede aplicar el análisis de cadenas no uniformes.

En este caso, las ecuaciones para la tensión son

$${displaystyle {begin{aligned} Tcos varphi &=T_{0},Tsin varphi > {1}{c}int T,ds,end{aligned}$$

Combinar da

$${displaystyle ctan varphi =int sec varphi ,ds}$$

y por diferenciación

$${displaystyle c=rho cos varphi }$$

donde ρ es el radio de curvatura.

La solución a esto es

$${displaystyle y=cln left(sec left({frac {x}{c}right)right),.}$$

En este caso, la curva tiene asíntotas verticales y esto limita el intervalo a πc. Otras relaciones son

$${displaystyle x=cvarphi ,quad s=ln left(tan left({frac {pi +2varphi Bueno...$$

La curva fue estudiada en 1826 por Davies Gilbert y, aparentemente de forma independiente, por Gaspard-Gustave Coriolis en 1836.

Recientemente, se demostró que este tipo de catenaria podría actuar como un componente básico de la metasuperficie electromagnética y se conoció como "catenaria de igual gradiente de fase".

Catenaria elástica

En una catenaria elástica, la cadena se reemplaza por un resorte que puede estirarse en respuesta a la tensión. Se supone que el resorte se estira de acuerdo con la Ley de Hooke. Específicamente, si p es la longitud natural de una sección del resorte, entonces la longitud del resorte con tensión T aplicado tiene longitud

$${displaystyle s=left(1+{frac {T}right)p,}$$

donde E es una constante igual a kp, donde k es la rigidez del resorte. En la catenaria el valor de T es variable, pero la relación sigue siendo válida a nivel local, por lo que

$${fnMicroc} {ds}{dp}=1+{frac.$$

Las ecuaciones para la tensión del resorte son

$${displaystyle Tcos varphi =T_{0},}$$

$${displaystyle Tsin varphi =lambda _{0}gp,}$$

de donde

$${displaystyle {frac {fnK}=tan} varphi ={frac {lambda ¿Por qué? {T_{0}{2}+lambda ¿Qué?$$

donde p es la longitud natural del segmento desde c a r y λ₀ es la masa por unidad de longitud del resorte sin tensión y g es la intensidad del campo gravitatorio. Escribir

$${displaystyle a={frac {f}{f}{f} {fnMicrosoft}} {fn}}} {fnMicrosoft}} {fn}}}}}} {fnMicrosoft}}}}}}} {fnK}}}} ¿Qué?$$

entonces

$${displaystyle {frac {fnK}=tan} varphi ={frac {fnh}fn}fnK}fnK}fnK}f}fnK}f}fn}fn}fn}fn}fnK}fn}fn}fn}f}fnK}f}f}fnK}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}fn}fn}f}f}f}f}f}f}f}f} {T_{0}{a}{sqrt {a^{2}+p^{2}},}$$

Entonces

$${displaystyle {begin{aligned}{frac {dx} {dx} {cos varphi ={frac} {T_{0} {[6pt]{frac {y} {ds} {f} {fnMicrosoft} {fn} {fnK}}} {fnK}} {fnK}} {fnK}}} {fnK}}}} {f}}}}\\fnMicrob}}}}}} {f}}}}}}}}}}}}}}}}}}}}}\\\\\\\\\\\\[6pt] {\\fn\\\\\\\\\\\\\fnMinMinMinMinMinMinMinMinMinMinMin}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} varphi ={frac {lambda _{0} {T},end{aligned}}$$

$${displaystyle {begin{alignedat}{3}{frac {dx}{}{={frac}{frac} {f}} {f}}} {f} {fnK}}} {f}} {f}}} {fnK} {fnMicroc}} {fnMicroc}}} {f}}} {f}} {f}}} {fn}} {f}}}}}} {fnMicroc}}}}} {f}}}}} {f}} {fnMicroc}}} {f}}}}}} {f}}}}}}}} {f}}}}}}} {f}}}}}} {f} {f}}}} {f}} {f} {f}}}}}}}}} {f}}} {f}}}}} {f} {f}} {f} {f}}}}}}}} {f} {f} {f} {f}}}}}} {f}} {f}}}}}}}}}}}}}}}}}}}}} {f}} {fnMicrosoft Sans Serif} {1} {T}+{frac} {1}{E}right) {a^{2}+p^{2}}}+{frac} {T_{0} {E}[6pt]{frac {y}{={frac} {f} {f} {f}} {fn0}} {f}}} {fn0}}} {fn0} {f}}}} {f}}}}}\fn9} {f}}}}}\\\\\\\\\\\fn9}\\\fnKfnKfnMicrocH00} {fn9}}}}}}}}}}}}}}}}\\\\\\\\\\\\fnK\fnK\\fnK\\fnK\\fnK\\\fnK\\\fnK\\fnMinK\\fn {fnMicrode ¿Qué? {ds} {dp} {fnMicroc} {T_{0}p}}left({frac} {1} {T}+{frac} {1}{E}right) {p}{sqrt {a^{2}+p^{2}}}+{frac} {T_{0}p},end{alignedat}}$$

La integración da las ecuaciones paramétricas

$${displaystyle {begin{aligned}x limit=aoperatorname {arsinh}left({frac {p}{a}}right)+{frac {T_{0}{E}p+alpha ,[6pt]y pulsa={sqrt {a^{2}+p^{2}}+{frac} {T_{0} {2Ea}p^{2}+beta ,end{aligned}}}$$

De nuevo, x y Los ejes y se pueden desplazar para que α y β puede tomarse como 0. Entonces

$${displaystyle {begin{aligned}x limit=aoperatorname {arsinh}left({frac {p}{a}}right)+{frac {T_{0}{E}p,[6pt]y {a^{2}+p^{2}}+{frac} {T_{0} {2Ea}p} {2}end{aligned}} {cH0}}} {cH0}}} {cH0}}}}} {cH0}}}}}}} {cH}}}}}}} {f}}} {f}} {f}}f}}}}}}}}}}} {f}}}}} {f}}}}}}}}}}}}f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$$

son ecuaciones paramétricas para la curva. En el límite rígido donde E es grande, la forma de la curva se reduce a la de una cadena no elástica.

Otras generalizaciones

Cadena bajo una fuerza general

Sin hacer suposiciones con respecto a la fuerza G que actúa sobre la cadena, se puede realizar el siguiente análisis.

Primero, sea T = T(s) la fuerza de tensión como una función de s. La cadena es flexible por lo que solo puede ejercer una fuerza paralela a sí misma. Dado que la tensión se define como la fuerza que la cadena ejerce sobre sí misma, la T debe ser paralela a la cadena. En otras palabras,

$${displaystyle mathbf {T} =Tmathbf {u} ,}$$

donde T es la magnitud de T y u es el vector unitario tangente.

Segundo, sea G = G(s) la fuerza externa por unidad de longitud que actúa sobre un pequeño segmento de una cadena en función de s. Las fuerzas que actúan sobre el segmento de la cadena entre s y s + Δs son la fuerza de tensión T(s + Δ s) en un extremo del segmento, la fuerza casi opuesta −T(s) en el otro extremo, y la fuerza externa que actúa sobre el segmento que es aproximadamente GΔs. Estas fuerzas deben equilibrarse para que

$${displaystyle mathbf {T} (s+Delta s)-mathbf {T} (s)+mathbf {G} Delta sapprox mathbf {0} ,}$$

Dividir por Δs y tomar el límite como Δs → 0 para obtener

$${fnMicroc {fnMithbf {T}{ds}+mathbf {G} =mathbf {0} ,}$$

Estas ecuaciones se pueden utilizar como punto de partida en el análisis de una cadena flexible que actúa bajo cualquier fuerza externa. En el caso de la catenaria estándar, G = (0, −λg) donde la cadena tiene masa λ por unidad de longitud y g es la fuerza del campo gravitatorio.