Curva tensión-deformación

Curva de estrés típica de un acero de bajo carbono

En ingeniería y ciencia de materiales, una curva de tensión-deformación para un material proporciona la relación entre tensión y deformación. Se obtiene aplicando carga gradualmente a un cupón de prueba y midiendo la deformación, a partir de la cual se pueden determinar la tensión y la deformación (ver prueba de tracción). Estas curvas revelan muchas de las propiedades de un material, como el módulo de Young, el límite elástico y la resistencia máxima a la tracción.

Definición

En términos generales, las curvas que representan la relación entre la tensión y la deformación en cualquier forma de deformación pueden considerarse como curvas de tensión-deformación. El esfuerzo y la deformación pueden ser normales, cortantes o mixtos, y también pueden ser uniaxiales, biaxiales o multiaxiales, incluso cambiar con el tiempo. La forma de deformación puede ser compresión, estiramiento, torsión, rotación, etc. Si no se menciona lo contrario, la curva tensión-deformación se refiere a la relación entre la tensión axial normal y la deformación axial normal de los materiales medidos en una prueba de tensión.

Esfuerzos y tensiones de ingeniería

Considere una barra de sección transversal original A₀ sometida a fuerzas iguales y opuestas F tirando de los extremos para que la barra quede bajo tensión. El material está experimentando una tensión definida como la relación entre la fuerza y el área de la sección transversal de la barra, así como un alargamiento axial:

σ σ =FA0ε ε =L− − L0L0=Δ Δ LL0{displaystyle {begin{aligned}sigma {fnMicroc {fnh}\cH33}\cH33}\cH0}\cH0}\cH0}\\cH0\cH0}\cH0\cH00} " {frac {L-L_{0}{L_{0}}={frac {Delta {fnK}} {fnK}} {fn}}} {fn}}} {fn}} {fn}} {fn}}} {fn}}}}} {fn}}}}}}}}}}}} {fn}}}}}}}}}}}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {

El subíndice 0 denota las dimensiones originales de la muestra. La unidad derivada del SI para la tensión es newton por metro cuadrado, o pascales (1 pascal = 1 Pa = 1 N/m²), y la deformación no tiene unidades. La curva tensión-deformación para este material se traza alargando la muestra y registrando la variación de la tensión con la deformación hasta que la muestra se fractura. Por convención, la deformación se establece en el eje horizontal y la tensión en el eje vertical. Tenga en cuenta que, por motivos de ingeniería, a menudo asumimos que el área de la sección transversal del material no cambia durante todo el proceso de deformación. Esto no es cierto ya que el área real disminuirá mientras se deforma debido a la deformación elástica y plástica. La curva basada en la sección transversal original y la longitud calibrada se denomina curva de tensión-deformación de ingeniería, mientras que la curva basada en el área y la longitud de la sección transversal instantáneas se denomina tensión real- curva de tensión. A menos que se indique lo contrario, generalmente se usa tensión-deformación de ingeniería.

Estrés y tensión reales

La diferencia entre la verdadera curva de estrés-entrenamiento y la curva de tensión de ingeniería

Debido a la contracción del área de la sección y al efecto ignorado del alargamiento desarrollado a un mayor alargamiento, la tensión y la deformación reales son diferentes de la tensión y la deformación de ingeniería.

σ σ t=FAε ε t=∫ ∫ δ δ LL{displaystyle {begin{aligned}sigma ¿Por qué? ¿Qué? ♪♪ {delta ¿Qué?

Aquí las dimensiones son valores instantáneos. Suponiendo que el volumen de la muestra se conserva y la deformación ocurre de manera uniforme,

A0L0=AL{displaystyle A_{0}L_{0}=AL

El esfuerzo y la deformación reales se pueden expresar mediante el esfuerzo y la deformación de ingeniería. Para el verdadero estrés,

σ σ t=FA=FA0A0A=FA0LL0=σ σ ()1+ε ε ){displaystyle sigma _{mathrm {t}={frac {F} {A}={frac} {F}{A_{0} {f} {f} {f}} {f}} {f}} {f}} {f}}}} {f} {f}}} {f}} {f}} {f}}} {f}}} {f}}}} {f}}}}}}}} {f} {f} {f}}}}} {f}}}} {f}f}}f}}}}}} {f} {f}}} {f} {f} {f}} {f}f}}}}}}}}}}}}}}}}}}}}}}}}}}} {f} {f} {f} {f} {f}f}f} {f} {f}}f}}}f}f}}}}f}}}}}}}}}}}}}}}} {fnK} {fnK}} {fnMicroc} {fnK}}} {f}} {fn}}}} {fn}} {fnMicroc}}}}}}} {fn}}} {f}}} {f}}}} {fnMicroc}} {F}{A_{0} {f} {f} {f}} {f}} {f}} {f}} {f}}}} {f} {f}}} {f}} {f}} {f}}} {f}}} {f}}}} {f}}}}}}}} {f} {f} {f}}}}} {f}}}} {f}f}}f}}}}}} {f} {f}}} {f} {f} {f}} {f}f}}}}}}}}}}}}}}}}}}}}}}}}}}} {f} {f} {f} {f} {f}f}f} {f} {f}}f}}}f}f}}}}f}}}}}}}}}}}}}}}} {L}{L_{0}=sigma (1+varepsilon)}

Para la cepa,

δ δ ε ε t=δ δ LL{displaystyle delta varepsilon _{mathrm {t}={frac {delta L} {L}}

Integre ambos lados y aplique la condición de contorno,

ε ε t=In⁡ ⁡ ()LL0)=In⁡ ⁡ ()1+ε ε ){displaystyle varepsilon _{mathrm {t} }=ln left({frac {L_{0}}right)=ln(1+varepsilon)}

Así que en una prueba de tensión, el estrés verdadero es mayor que el estrés de ingeniería y la tensión verdadera es menor que la tensión de ingeniería. Por lo tanto, un punto que define la verdadera curva de estrés-entrenamiento es desplazado hacia arriba y hacia la izquierda para definir la curva equivalente del estrés-estrés de ingeniería. La diferencia entre las tensiones y cepas verdaderas e ingeniería aumentará con la deformación plástica. En cepas bajas (como la deformación elástica), las diferencias entre los dos son insignificantes. En cuanto al punto de fuerza tensil, es el punto máximo en la curva de tensión de ingeniería, pero no es un punto especial en la verdadera curva de estrés-estrés. Debido a que el estrés de ingeniería es proporcional a la fuerza aplicada a lo largo de la muestra, el criterio para la formación de cuello se puede establecer como δ δ F=0.{displaystyle delta F=0.}

δ δ F=σ σ tδ δ A+Aδ δ σ σ t=0− − δ δ AA=δ δ σ σ tσ σ t{displaystyle {begin{aligned} F=sigma _{text{t}},delta A+A,delta sigma _{text{t}}=0\\c {delta A}{A}={frac {delta sigma _{mathrm {t}{sigma _{mathrm {t}}}}}}end{aligned}}} {}}} {f}} {fn}}} {f}}} {f}}}}} {f}}}}}}}}}}}} {f}}}}}}}}}}}}}}}} {f}}}}}}}}}}}} {f}}}}

Este análisis sugiere la naturaleza del punto de máxima resistencia a la tracción (UTS). El efecto de fortalecimiento del trabajo se equilibra exactamente con la reducción del área de la sección en el punto UTS.

Después de la formación del cuello, la muestra sufre una deformación heterogénea, por lo que las ecuaciones anteriores no son válidas. La tensión y la deformación en la estricción se pueden expresar como:

σ σ t=FAneckε ε t=In⁡ ⁡ ()A0Aneck){displaystyle {begin{aligned}sigma - ¿Qué? {F}{A_{mathrm {Neck}\\\fnMicrosoft} ¿Qué? }=ln left({frac {A_{0}{A_{mathrm {}}}right)end{aligned}}}}}

Se suele utilizar una ecuación empírica para describir la relación entre la tensión real y la deformación real.

σ σ t=K()ε ε t)n{displaystyle sigma _{mathrm {t}=K(varepsilon _{mathrm {t})^{n}

Aquí, n es el exponente de endurecimiento por deformación y K es el coeficiente de fuerza. n es una medida del comportamiento de endurecimiento por trabajo de un material. Los materiales con una n más alta tienen una mayor resistencia al estrechamiento. Normalmente, los metales a temperatura ambiente tienen n que oscilan entre 0,02 y 0,5.

Etapas

En la figura 1 se muestra un diagrama esquemático de la curva de tensión-deformación del acero con bajo contenido de carbono a temperatura ambiente. Hay varias etapas que muestran diferentes comportamientos, lo que sugiere diferentes propiedades mecánicas. Para aclarar, los materiales pueden perder una o más etapas que se muestran en la figura 1, o tener etapas totalmente diferentes.

La primera etapa es la región elástica lineal. El esfuerzo es proporcional a la deformación, es decir, obedece la ley general de Hooke, y la pendiente es el módulo de Young. En esta región, el material sufre únicamente deformación elástica. El final de la etapa es el punto de inicio de la deformación plástica. El componente de tensión de este punto se define como límite elástico (o límite elástico superior, UYP para abreviar).

La segunda etapa es la región de endurecimiento por deformación. Esta región comienza cuando la tensión va más allá del punto de fluencia, alcanzando un máximo en el punto de resistencia máxima, que es la tensión máxima que se puede soportar y se denomina resistencia máxima a la tracción (UTS). En esta región, la tensión aumenta principalmente a medida que el material se alarga, excepto que para algunos materiales como el acero, hay una región casi plana al principio. La tensión de la región plana se define como el punto de fluencia inferior (LYP) y resulta de la formación y propagación de bandas de Lüders. Explícitamente, la deformación plástica heterogénea forma bandas en el límite elástico superior y estas bandas se extienden con la deformación a lo largo de la muestra en el límite elástico inferior. Después de que la muestra se deforma nuevamente de manera uniforme, el aumento de la tensión con el progreso de la extensión resulta del fortalecimiento del trabajo, es decir, las dislocaciones densas inducidas por la deformación plástica dificultan el movimiento posterior de las dislocaciones. Para superar estos obstáculos, se debe aplicar un esfuerzo cortante resuelto más alto. A medida que se acumula la tensión, se refuerza el fortalecimiento del trabajo, hasta que la tensión alcanza la máxima resistencia a la tracción.

La tercera etapa es la región de estrechamiento. Más allá de la resistencia a la tracción, se forma un estrechamiento donde el área de la sección transversal local se vuelve significativamente más pequeña que el promedio. La deformación del estrechamiento es heterogénea y se reforzará a medida que la tensión se concentre más en la sección pequeña. Tal retroalimentación positiva conduce a un rápido desarrollo de estrechamiento y conduce a la fractura. Tenga en cuenta que aunque la fuerza de tracción está disminuyendo, el fortalecimiento del trabajo aún está progresando, es decir, el esfuerzo real sigue creciendo pero el esfuerzo de ingeniería disminuye porque no se considera el área de la sección que se contrae. Esta región termina con la fractura. Después de la fractura, se puede calcular el porcentaje de elongación y reducción en el área de la sección.

Clasificación

Curva de estrés para materiales frágiles en comparación con materiales dútiles

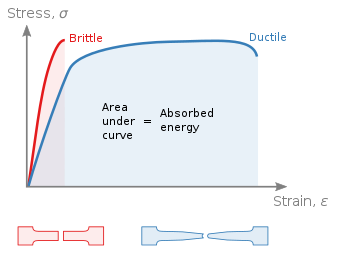
Es posible distinguir algunas características comunes entre las curvas de tensión-deformación de varios grupos de materiales y, sobre esta base, dividir los materiales en dos grandes categorías; a saber, los materiales dúctiles y los materiales frágiles.

Materiales dúctiles

Los materiales dúctiles, incluido el acero estructural y muchos otros metales, se caracterizan por su capacidad de ceder a temperaturas normales. Por ejemplo, el acero bajo en carbono generalmente presenta una relación tensión-deformación muy lineal hasta un punto de fluencia bien definido. La porción lineal de la curva es la región elástica, y la pendiente de esta región es el módulo de elasticidad o módulo de Young. El flujo plástico se inicia en el punto de fluencia superior y continúa en el punto de fluencia inferior.

La aparición del punto de fluencia superior está asociada con la fijación de dislocaciones en el sistema. La deformación permanente ocurre una vez que las dislocaciones se ven obligadas a moverse más allá de los puntos de fijación. Inicialmente, esta deformación permanente no se distribuye uniformemente a lo largo de la muestra. Durante este proceso, las dislocaciones escapan de las atmósferas de Cottrell dentro del material. Las bandas deslizantes resultantes aparecen en el punto de fluencia inferior y se propagan a lo largo de la longitud de referencia, con tensión constante, hasta que se alcanza la deformación de Lüders y la deformación se vuelve uniforme.

Más allá de la deformación de Lüders, la tensión aumenta debido al endurecimiento por deformación hasta que alcanza la tensión máxima de tracción. Durante esta etapa, el área de la sección transversal disminuye uniformemente a lo largo de la longitud de referencia, debido a la incompresibilidad del flujo plástico (no al efecto Poisson, que es un fenómeno elástico). Luego comienza un proceso de formación de cuellos, que termina en un 'taza y cono' Fractura característica de los materiales dúctiles.

La aparición de cuellos en materiales dúctiles está asociada con inestabilidad geométrica en el sistema. Debido a la falta de homogeneidad natural del material, es común encontrar algunas regiones con pequeñas inclusiones o porosidad, dentro del material o en su superficie, donde la deformación se concentrará, lo que conducirá a una reducción local del área de la sección transversal. Para una deformación inferior a la deformación última por tracción, el aumento de la tasa de endurecimiento por trabajo en esta región será mayor que la tasa de reducción del área, lo que hará que esta región sea más difícil de deformar que otras, de modo que se elimine la inestabilidad, es decir, el material aumenta en homogeneidad antes de alcanzar la deformación final. Sin embargo, más allá de esto, la tasa de endurecimiento por trabajo disminuirá, de modo que una región con un área más pequeña es más débil que las regiones cercanas, por lo tanto, la reducción del área se concentrará en esta región y el cuello se volverá más y más pronunciado hasta la fractura. Una vez que se ha formado el cuello en el material, se concentra más deformación plástica en el cuello mientras que el resto del material sufre una contracción elástica debido a la disminución de la fuerza de tracción.

La curva de tensión-deformación de un material dúctil se puede aproximar mediante la ecuación de Ramberg-Osgood. Esta ecuación es fácil de implementar y solo requiere el límite elástico del material, la resistencia máxima, el módulo elástico y el porcentaje de elongación.

Materiales frágiles

Los materiales frágiles, que incluyen el hierro fundido, el vidrio y la piedra, se caracterizan por el hecho de que la ruptura ocurre sin ningún cambio previo perceptible en la tasa de elongación, a veces se fracturan antes de ceder.

Los materiales quebradizos, como el hormigón o la fibra de carbono, no tienen un punto de fluencia bien definido y no se endurecen por deformación. Por lo tanto, la resistencia última y la resistencia a la rotura son las mismas. Los materiales quebradizos típicos como el vidrio no muestran ninguna deformación plástica pero fallan mientras la deformación es elástica. Una de las características de una falla por fragilidad es que las dos partes rotas se pueden volver a ensamblar para producir la misma forma que el componente original, ya que no habrá formación de cuello como en el caso de los materiales dúctiles. Una curva típica de tensión-deformación para un material frágil será lineal. Para algunos materiales, como el hormigón, la resistencia a la tracción es insignificante en comparación con la resistencia a la compresión y se supone cero para muchas aplicaciones de ingeniería. Las fibras de vidrio tienen una resistencia a la tracción más fuerte que el acero, pero el vidrio a granel generalmente no la tiene. Esto se debe al factor de intensidad de tensión asociado con defectos en el material. A medida que aumenta el tamaño de la muestra, también crece el tamaño esperado del defecto más grande.