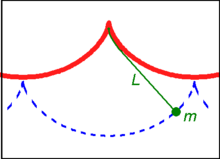
Curva tautocrona

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Concepto en geometría

Cuatro bolas deslizan hacia abajo una curva de cicloide de diferentes posiciones, pero llegan al fondo al mismo tiempo. Las flechas azules muestran la aceleración de los puntos a lo largo de la curva. En la parte superior está el diagrama de tiempo-posición.

Objetos que representan la curva de tautocrone

Una tautocrona o curva isócrona (del prefijo griego tauto- que significa mismo o iso- igual, y crono tiempo) es la curva en la que el tiempo que tarda un objeto que se desliza sin fricción en gravedad uniforme hasta su punto más bajo es independiente de su punto de partida en la curva. La curva es una cicloide, y el tiempo es igual a π por la raíz cuadrada del radio (del círculo que genera la cicloide) sobre la aceleración de la gravedad. La curva tautocrona está relacionada con la curva braquistocrona, que también es una cicloide.

El problema de la tautocronía

Christiaan Huygens, Horologium oscillatorium sive de motu pendulorum, 1673

Fue en el punto de prueba de mano izquierda del Pequod, con la piedra de jabón que me rodeaba diligentemente, que fui golpeado indirectamente por el hecho notable, que en la geometría todos los cuerpos deslizando a lo largo del cicloide, mi piedra de jabón, por ejemplo, descenderán de cualquier punto en precisamente el mismo tiempo.

Moby Dick por Herman Melville, 1851

El problema de la tautocronía, el intento de identificar esta curva, fue resuelto por Christiaan Huygens en 1659. Probó geométricamente en su Horologium Oscillatorium, publicado originalmente en 1673, que la curva es una cicloide.

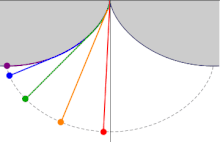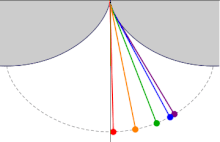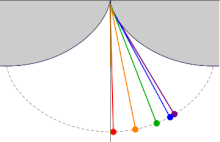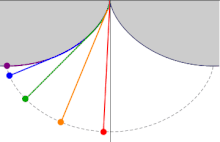
En un cicloides cuyo eje se erige en el perpendicular y cuyo vértice se encuentra en la parte inferior, los tiempos de descenso, en los que un cuerpo llega al punto más bajo del vértice después de haber salido de cualquier punto en el cicloides, son iguales entre sí...

El cicloide es dado por un punto en un círculo de radio $r$ trazando una curva mientras el círculo rueda a lo largo de la $x$ axis, como:

{displaystyle {begin{aligned}x&=r(theta -sin theta)\y&=r(1-cos theta),end{aligned}}}

Huygens también demostró que el tiempo de descenso es igual al tiempo que un cuerpo tarda en caer verticalmente la misma distancia que el diámetro del círculo que genera el cicloide, multiplicado por $pi /2$ . En términos modernos, esto significa que el tiempo de descenso es ${textstyle pi {sqrt {r/g}}}$ , donde $r$ es el radio del círculo que genera la cicloides, y $g$ es la gravedad de la Tierra, o más exactamente, la aceleración gravitacional de la tierra.

Cinco péndulos cicloidales isocronos con diferentes amplitudes

Esta solución se usó más tarde para resolver el problema de la curva braquistócrona. Johann Bernoulli resolvió el problema en un artículo (Acta Eruditorum, 1697).

Esquema de un péndulo cicloides

Huygens estudió más de cerca el problema de la tautocronía cuando se dio cuenta de que un péndulo, que sigue una trayectoria circular, no era isócrono y, por lo tanto, su reloj de péndulo mantendría un tiempo diferente dependiendo de qué tan lejos se balanceara el péndulo. Después de determinar la ruta correcta, Christiaan Huygens intentó crear relojes de péndulo que usaban una cuerda para suspender la lenteja y las mejillas cerca de la parte superior de la cuerda para cambiar la ruta a la curva tautócrona. Estos intentos resultaron inútiles por varias razones. Primero, la flexión de la cuerda causa fricción, cambiando el tiempo. En segundo lugar, había fuentes mucho más significativas de errores de tiempo que abrumaban cualquier mejora teórica que ayudara a viajar en la curva tautocrona. Finalmente, el "error circular" de un péndulo disminuye a medida que disminuye la longitud de la oscilación, por lo que mejores escapes de reloj podrían reducir en gran medida esta fuente de inexactitud.

Más tarde, los matemáticos Joseph Louis Lagrange y Leonhard Euler aportaron una solución analítica al problema.

Solución lagrangiana

Si la posición de la partícula es parametrizada por la arclength $s () t)$ desde el punto más bajo, la energía cinética es proporcional a ${displaystyle {dot {s}}^{2}.}$ La energía potencial es proporcional a la altura $Sí. () s)$ . Una manera de que la curva puede ser un isocrono es si el Lagrangiano es el de un simple oscilador armónico: la altura de la curva debe ser proporcional al cuadrado de la arclength.

{displaystyle y(s)=s^{2},}

donde la constante de proporcionalidad se ha establecido en 1 cambiando las unidades de longitud.

La forma diferencial de esta relación es

{displaystyle {begin{aligned}dy&=2s,ds,\dy^{2}&=4s^{2},ds^{2}=4yleft(dx^{2}+dy^{2}right),end{aligned}}}

que elimina $s$ y deja una ecuación diferencial para $dx$ y $dy$ . Para encontrar la solución, integre para $x$ en términos de $y$ :

{displaystyle {begin{aligned}{frac {dx}{dy}}&={frac {sqrt {1-4y}}{2{sqrt {y}}}},\x&=int {sqrt {1-4u^{2}}},du,end{aligned}}}

Donde ${displaystyle u={sqrt {y}}}$ . Esta parte integral es el área bajo un círculo, que se puede cortar naturalmente en un triángulo y una cuña circular:

{displaystyle {begin{aligned}x&={tfrac {1}{2}}u{sqrt {1-4u^{2}}}+{tfrac {1}{4}}arcsin 2u,\y&=u^{2}.end{aligned}}}

Para ver que es una cicloides extrañamente parametrizada, cambiar variables para desenredar las partes trascendental y algebraica definiendo el ángulo ${displaystyle theta =arcsin 2u}$ . Este rendimiento

{displaystyle {begin{aligned}8x&=2sin theta cos theta +2theta =sin 2theta +2theta\8y&=2sin ^{2}theta =1-cos 2thetaend{aligned}}}

que es la parametrización estándar, excepto la escala de $x, y$ y $θ$ .

"Gravedad virtual" solución

La solución más simple del problema de tautocron es observar una relación directa entre el ángulo de una inclinación y la gravedad que siente una partícula sobre la inclinación. Una partícula sobre una inclinación vertical de 90° experimenta aceleración gravitacional completa $g$ , mientras que una partícula en un plano horizontal experimenta una aceleración gravitacional cero. En ángulos intermedios, la aceleración debida a la "gravación virtual" por la partícula es ${displaystyle gsin theta }$ . Note que $theta$ se mide entre el tangente a la curva y el horizontal, con ángulos por encima de la horizontal que se trata como ángulos positivos. Así, $theta$ de los $-pi /2$ a $pi /2$ .

La posición de una masa medida a lo largo de una curva de tautocrono, $s(t)$ , debe obedecer la siguiente ecuación diferencial:

{displaystyle {frac {d^{2}s}{{dt}^{2}}}=-omega ^{2}s}

que, junto con las condiciones iniciales ${displaystyle s(0)=s_{0}}$ y ${displaystyle s'(0)=0}$ , tiene solución:

{displaystyle s(t)=s_{0}cos omega t}

Se puede verificar fácilmente tanto que esta solución resuelve la ecuación diferencial como que una partícula alcanzará $s=0$ a la vez ${displaystyle pi /2omega }$ desde cualquier posición inicial $s_{0}$ . El problema es ahora construir una curva que hará que la masa obedezca al movimiento anterior. La segunda ley de Newton muestra que la fuerza de gravedad y la aceleración de la masa están relacionadas por:

{displaystyle {begin{aligned}-gsin theta &={frac {d^{2}s}{{dt}^{2}}}\&=-omega ^{2}s,end{aligned}}}

La apariencia explícita de la distancia, $s$ , es problemático, pero podemos diferenciar para obtener una forma más manejable:

{displaystyle {begin{aligned}gcos theta ,dtheta &=omega ^{2},ds\Longrightarrow ds&={frac {g}{omega ^{2}}}cos theta ,dtheta end{aligned}}}

Esta ecuación relaciona el cambio en el ángulo de la curva con el cambio en la distancia a lo largo de la curva. Ahora utilizamos trigonometría para relacionar el ángulo $theta$ a las longitudes diferenciales $dx$ , $dy$ y $ds$ :

{displaystyle {begin{aligned}ds={frac {dx}{cos theta }}\ds={frac {dy}{sin theta }}end{aligned}}}

Replacing $ds$ con $dx$ en la ecuación anterior nos permite resolver para $x$ en términos de $theta$ :

{displaystyle {begin{aligned}ds&={frac {g}{omega ^{2}}}cos theta ,dtheta \{frac {dx}{cos theta }}&={frac {g}{omega ^{2}}}cos theta ,dtheta \dx&={frac {g}{omega ^{2}}}cos ^{2}theta ,dtheta \&={frac {g}{2omega ^{2}}}left(cos 2theta +1right)dtheta \x&={frac {g}{4omega ^{2}}}left(sin 2theta +2theta right)+C_{x}end{aligned}}}

Asimismo, también podemos expresar $ds$ en términos de $dy$ y resolver para $y$ en términos de $theta$ :

{displaystyle {begin{aligned}ds&={frac {g}{omega ^{2}}}cos theta ,dtheta \{frac {dy}{sin theta }}&={frac {g}{omega ^{2}}}cos theta ,dtheta \dy&={frac {g}{omega ^{2}}}sin theta cos theta ,dtheta \&={frac {g}{2omega ^{2}}}sin 2theta ,dtheta \y&=-{frac {g}{4omega ^{2}}}cos 2theta +C_{y}end{aligned}}}

Sustitución ${displaystyle phi =2theta }$ y ${textstyle r={frac {g}{4omega ^{2}}},}$ , vemos que estas ecuaciones paramétricas para $x$ y $y$ son los de un punto en un círculo de radio $r$ rodando a lo largo de una línea horizontal (cicloide), con el centro del círculo en las coordenadas ${displaystyle (C_{x}+rphiC_{y})}$ :

{displaystyle {begin{aligned}x&=rleft(sin phi +phi right)+C_{x}\y&=-rcos phi +C_{y}end{aligned}}}

Note que $phi$ rangos desde ${displaystyle -pi leq phi leq pi }$ . Es típico de fijar ${displaystyle C_{x}=0}$ y ${displaystyle C_{y}=r}$ para que el punto más bajo de la curva coincida con el origen. Por lo tanto:

{displaystyle {begin{aligned}x&=rleft(phi +sin phi right)\y&=rleft(1-cos phi right)\end{aligned}}}

Solving for $omega$ y recordando eso ${displaystyle T={frac {pi }{2omega }}}$ es el tiempo requerido para el descenso, siendo un cuarto de un ciclo entero, encontramos el tiempo de descenso en términos del radio $r$ :

{displaystyle {begin{aligned}r&={frac {g}{4omega ^{2}}}\omega &={frac {1}{2}}{sqrt {frac {g}{r}}}\T&=pi {sqrt {frac {r}{g}}}\end{aligned}}}

(Basado libremente en Proctor, págs. 135–139)

La solución de Abel

Niels Henrik Abel atacó una versión generalizada del problema de tautocrone (El problema mecánico de Abel), es decir, dada una función ${displaystyle T(y)}$ que especifica el tiempo total de descenso para una determinada altura de inicio, encontrar una ecuación de la curva que produce este resultado. El problema de tautocron es un caso especial del problema mecánico de Abel cuando ${displaystyle T(y)}$ es una constante.

La solución de Abel comienza con el principio de la conservación de la energía – ya que la partícula es sin fricción, y por lo tanto no pierde energía al calor, su energía cinética en cualquier punto es exactamente igual a la diferencia de la energía potencial gravitacional desde su punto de partida. La energía cinética es ${textstyle {frac {1}{2}}mv^{2}}$ , y como la partícula se limita a moverse a lo largo de una curva, su velocidad es simplemente ${displaystyle {dell }/{dt}}$ , donde $ell$ es la distancia medida a lo largo de la curva. Del mismo modo, la energía potencial gravitacional ganada en caer de una altura inicial $y_{0}$ a una altura $y$ es ${displaystyle mg(y_{0}-y)}$ , por lo tanto:

{displaystyle {begin{aligned}{frac {1}{2}}mleft({frac {dell }{dt}}right)^{2}&=mg(y_{0}-y)\{frac {dell }{dt}}&=pm {sqrt {2g(y_{0}-y)}}\dt&=pm {frac {dell }{sqrt {2g(y_{0}-y)}}}\dt&=-{frac {1}{sqrt {2g(y_{0}-y)}}}{frac {dell }{dy}},dyend{aligned}}}

En la última ecuación, hemos anticipado escribir la distancia que queda a lo largo de la curva como una función de altura ( ${displaystyle ell (y))}$ , reconoció que la distancia restante debe disminuir a medida que aumenta el tiempo (porque el signo menos), y utilizó la regla de cadena en la forma ${textstyle dell ={frac {dell }{dy}}dy}$ .

Ahora nos integramos desde $y=y_{0}$ a $y=0$ para que el tiempo total requerido para la caída de la partícula:

{displaystyle T(y_{0})=int _{y=y_{0}}^{y=0},dt={frac {1}{sqrt {2g}}}int _{0}^{y_{0}}{frac {1}{sqrt {y_{0}-y}}}{frac {dell }{dy}},dy}

Esto se llama Ecuación integral de Abel y nos permite calcular el tiempo total requerido para que una partícula caiga a lo largo de una curva dada (para la cual ${displaystyle {dell }/{dy}}$ sería fácil de calcular). Pero el problema mecánico de Abel requiere el contrario – dado $T(y_0),$ , deseamos encontrar ${displaystyle f(y)={dell }/{dy}}$ , de la cual una ecuación para la curva seguiría de manera directa. Para proceder, observamos que la parte integral de la derecha es la convolución de ${displaystyle {dell }/{dy}}$ con ${displaystyle {1}/{sqrt {y}}}$ y por lo tanto tomar la transformación Laplace de ambos lados con respecto a la variable $y$ :

{displaystyle {mathcal {L}}[T(y_{0})]={frac {1}{sqrt {2g}}}{mathcal {L}}left[{frac {1}{sqrt {y}}}right]F(s)}

Donde ${displaystyle F(s)={mathcal {L}}{left[{dell }/{dy}right]}}$ . Desde ${textstyle {mathcal {L}}{left[{1}/{sqrt {y}}right]}={sqrt {{pi }/{s}}}}$ , ahora tenemos una expresión para la transformación de Laplace ${displaystyle {dell }/{dy}}$ en términos de la transformación de Laplace ${displaystyle T(y_{0})}$ :

{displaystyle {mathcal {L}}left[{frac {dell }{dy}}right]={sqrt {frac {2g}{pi }}}s^{frac {1}{2}}{mathcal {L}}[T(y_{0})]}

Esto es lo que podemos ir sin especificar ${displaystyle T(y_{0})}$ . Una vez ${displaystyle T(y_{0})}$ es conocido, podemos calcular su transformación de Laplace, calcular la transformación de Laplace ${displaystyle {dell }/{dy}}$ y luego tomar la transformación inversa (o tratar de) para encontrar ${displaystyle {dell }/{dy}}$ .

Para el problema de tautocrone, $T(y_0) = T_0,$ es constante. Desde la transformación de Laplace de 1 es ${displaystyle {1}/{s}}$ , es decir, ${textstyle {mathcal {L}}[T(y_{0})]={T_{0}}/{s}}$ , encontramos la función de la forma ${textstyle f(y)={dell }/{dy}}$ :

{displaystyle {begin{aligned}F(s)={mathcal {L}}{left[{frac {dell }{dy}}right]}&={sqrt {frac {2g}{pi }}}s^{frac {1}{2}}{mathcal {L}}[T_{0}]\&={sqrt {frac {2g}{pi }}}T_{0}s^{-{frac {1}{2}}}end{aligned}}}

Usando nuevamente la transformada de Laplace anterior, invertimos la transformada y concluimos:

{displaystyle {frac {dell }{dy}}=T_{0}{frac {sqrt {2g}}{pi }}{frac {1}{sqrt {y}}}}

Se puede demostrar que la cicloides obedece esta ecuación. Necesita un paso más para hacer la integral con respecto a $y$ para obtener la expresión de la forma del camino.

(Simmons, Sección 54).

Contenido relacionado

Más resultados...