Cúpula (geometría)

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

En geometría, una cúpula es un sólido formado al unir dos polígonos, uno (la base) con el doble de aristas que el otro, mediante una banda alterna de triángulos isósceles y rectángulos. Si los triángulos son equiláteros y los rectángulos son cuadrados, mientras que la base y su cara opuesta son polígonos regulares, las cúpulas triangular, cuadrada y pentagonal cuentan entre los sólidos de Johnson y pueden formarse tomando secciones del cuboctaedro, rombicuboctaedro, y rombicosidodecaedro, respectivamente.

Una cúpula puede verse como un prisma donde uno de los polígonos se ha colapsado por la mitad fusionando vértices alternos.

A una cúpula se le puede dar un símbolo Schläfli extendido ${n} || t{n},$ que representa un polígono regular ${n}$ unido por un paralelo de su truncamiento, $t{n}$ o ${2 n}.$

Las cúpulas son una subclase de los prismatoides.

Su dual contiene una forma que es una especie de soldadura entre la mitad de un trapezoedro de lados $n$ y un $Pirámide de 2 n$ caras.

Ejemplos

Familia de cúpula convexa
v
t
e
n	2	3	4	5	6	7	8
Símbolo Schläfli	${2}$	${3}$	${4}$	${5}$	${6}$	${7}$	${8}$
Cupola	Cupola digonal	Triangular cupola	Copa cuadrado	Cupola pentagonal	Cupola hexagonal (Flat)	Cupola heptagonal (Cara no regular)	Cupola Octagonal (Cara no regular)
Relacionados uniforme polihedra	Rhombohedron	Cuboctahedron	Rhombicuboctahedron	Rhombicosidodecahedron	Tiling Rhombitrihexagonal	Tiling Rhombitriheptagonal	Tiling Rhombitrioctagonal

Los tres poliedros mencionados anteriormente son las únicas cúpulas convexas no triviales con caras regulares: La "cúpula hexagonal" es una figura plana y el prisma triangular podría considerarse una "cúpula" de grado 2 (la cúpula de un segmento de recta y un cuadrado). Sin embargo, se pueden construir cúpulas de polígonos de mayor grado con caras triangulares y rectangulares irregulares.

Coordenadas de los vértices

La definición de la cúpula no requiere que la base (o el lado opuesto a la base, que se puede llamar la parte superior) sea un polígono regular, pero es conveniente considerar el caso donde la cúpula tiene su simetría máxima, $C n v$ . En ese caso, la parte superior es regular $n$ -gon, mientras que la base es regular $2 n$ - o un $2 n$ -gon que tiene dos longitudes laterales diferentes alternando y los mismos ángulos que un regular $2 n$ - Vete. Es conveniente fijar el sistema de coordenadas para que la base se encuentre en el $xy$ -plano, con la parte superior en un plano paralelo al $xy$ - Avión. El $z$ - El eje es $n$ - el eje, y los planos del espejo pasan por el $z$ -eje y bisecte los lados de la base. También tocan los lados o los ángulos del polígono superior, o ambos. (Si) $n$ es incluso, la mitad de los planos del espejo bisectan los lados del polígono superior y la mitad bisectan los ángulos, mientras que si $n$ es extraño, cada bisectos de plano espejo un lado y un ángulo del polígono superior.) Los vértices de la base pueden ser designados ${displaystyle V_{1}$ a través de ${displaystyle V_{2n},}$ mientras que los vértices del polígono superior pueden ser designados ${displaystyle V_{2n+1}$ a través de ${displaystyle V_{3n}.$ Con estas convenciones, las coordenadas de los vértices se pueden escribir como:

{fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fn} {fn} {fn} {fn} {fnMicrosoft}} {fn}} {b}} {b}} {b} {b}}} {b}}}} {b}}}}}}}}}}}}}} {b}}b}}}}}}}}}} {b} {b}} {b}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {b} {b}}}} {b} {b} {b} {b}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} j} {n}}-alpha right), limitr_{b}sin left({frac {2pi [2pt]V_{2n+j}: {biggl} {biggr]}[2pt]V_{2n+j}: {biggl (}r_{t}cos {frac {pic} {fn} {fn} {fn}fnfn}fnfnfnfn} {fn} {fn} {fn}} {fn}}}}

donde $j = 1, 2,..., n$ .

Desde los polígonos ${displaystyle V_{1}V_{2n+2}V_{2n+1}$ etc. son rectángulos, esto pone una limitación en los valores de ${displaystyle.$ La distancia ${displaystyle {bigl Silencio.$ es igual a

{fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} }{n}-alpha right)-2cos left({tfrac {2pi}{n}-alpha right)cos alpha +cos ^{2}alpha right]+left[sin ^{2}left({tfrac {2pi }{n}}}alpha right)-2sin left({tfrac {2pi }{n}}alpha right)sin alpha {fn} {fn} {fn} {fn}fn} {fn} {fn} {fn} {fn}fn} {fn}fn} {fn}fnfn} {fn} {fnfn}fn}fnfnfn}}fn}fn}fn}}fnfn}nncH00}c}ccH00}ccH00}cccH00cH00}cccH00}cH00}c}cccH00}ccH00}ccH00}}cH00}ccH00}cH00}cH00}cH00}cH00}}cH00}cH00}cH00}cH00}}ccH

mientras que la distancia ${displaystyle {bigl Silencio!$ es igual a

{displaystyle {begin{aligned} {fnMicroc} {cHFF} Está bien. ################################################################################################################################################################################################################################################################ {fn}}\\fnh} {fn} {fn} {fn}} {fn} {fn} {fn} {fn}fn} {fn} {fn}}}}\\\\\\\\fn}\\\\fn}\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\fn}}\\\\\\\\\\\\\\\\\\\fn}}\\\\\\\\\\\\\\\\\\\\ - ¿Qué? } {n}+1right]+sin ^{2}{tfrac {pi} {}}}\=\\\\fn}}\\\fn}\\\\\\\\\\\\\\\\fn}\\\\\\\\\\\\\\\\\\\\fn}}\\\\\\\\\\\\\\\fn}}\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\}}}}}}}}}}}}}}\\\\\\\\\\\\\ ¿Qué? {2left[1-cos {fn}}end{aligned}}} {fn} {fn}}}} {fn}}}}}} {fn} {fn}} {fn} {fn}}} {fn}}}}}}}}fnfnf}}}}} {f}}}}}}}}}}}}fnfn}fn}fn}}f}fn}}fnfn}}f}fnfn}fn}nfnf}fnfnfnfnfn}fnfn}fnfn}fnfn}fnfnfnfn}fn}fn}fn}fn}fn}fn}fn}fn}fn}}}fn

Deben ser iguales, y si este borde común se denota por $s$ ,

{displaystyle {begin{aligned}r_{b} {s}{sqrt {2left[1-cos left({tfrac {2pi [4pt]r_{t={frac] {fn} {fn}}}end{aligned}

Estos valores deben insertarse en las expresiones para las coordenadas de los vértices dadas anteriormente.

Cúpulas estelares

Familia de estrella-cupolae
v
t
e
${} n / d}$	4	5	7	8
3	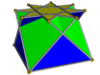{4/3} Casilla cruzada	{5/3} Pentragramamiccupola cruzada	{7/3} Heptagrammiccupola	{8/3} Octagrammiccupola
5	—	—	{7/5} Heptagramamiccupola cruzada	{8/5} Octogramamiccupola cruzada

Familia de Star-cuploids
v
t
e
$n . d$	3	5	7
2	{3/2} Superficiloide triangular	{5/2} Pentagramamiccuploide	{7/2} Heptagrammic Cuploide
4	—	{5/4} Pentagonalcuploide cruzado	{7/4} Heptagramas cruzados Cuploide

Existen cúpulas en forma de estrella para todas las bases ${n / d}$ donde $6 /5 < n / d < 6$ y $d$ es impar. En los límites, las cúpulas se colapsan en figuras planas: más allá de los límites, los triángulos y los cuadrados ya no pueden cubrir la distancia entre los dos polígonos (todavía se puede hacer si los triángulos o los cuadrados son irregulares). Cuando $d$ es par, la base inferior ${2 n / d}$ se vuelve degenerado: podemos formar una cupoloide o una semicúpula retirando esta cara degenerada y, en su lugar, dejando que los triángulos y los cuadrados se conecten. el uno al otro aquí. En particular, el tetrahemihexaedro puede verse como un cupoloide {3/2}. Todas las cúpulas son orientables, mientras que los cupoloides no son orientables. Cuando $n / d > 2$ en un cupoide, los triángulos y cuadrados no cubren toda la base, y se deja una pequeña membrana en la base que simplemente cubre el espacio vacío. Por lo tanto, los cupoloides {5/2} y {7/2} que se muestran arriba tienen membranas (no rellenas), mientras que los cupoloides {5/4} y {7/4} que se muestran arriba no.

La altura $h$ de un ${n /< i>d}$ -cúpula o cupoloide viene dada por la fórmula

{displaystyle h={sqrt {1-{frac {1}{4sin ^{2}{frac {pi} ♪♪

h = 0

n / d = 6

n / d = 6/5

h

n / d = 2

En las imágenes de arriba, a las cúpulas de las estrellas se les ha dado un esquema de color consistente para ayudar a identificar sus caras: la base ${n / d}$ -gon es rojo, la base ${2n / d}$ -gon es amarilla, los cuadrados son azules y los triángulos son verdes. Los cupoloides tienen la base ${n / d}$ -gón rojo, los cuadrados amarillos y los triángulos azules, como la otra base ha sido retirada.

Anticúpula

Una $n$ -anticupola-gonal se construye a partir de una $2 n$ base gonal, $3 n$ triángulos como dos tipos y una n-parte superior-gonal. Para $n = 2$ , la cara superior del digon se reduce a un solo borde. Los vértices del polígono superior están alineados con los vértices del polígono inferior. La simetría es $C n v$ , orden $2 n .$

No se puede construir una anticúpula con todas las caras regulares, aunque algunas se pueden hacer regulares. Si el $n$ -gon y los triángulos superiores son regulares, la base $2 n$ -gon no puede ser plano y regular. En tal caso, $n = 6$ genera un hexágono regular y los triángulos equiláteros circundantes de un mosaico hexagonal chato, que se puede cerrar en un polígono de volumen cero. con la base un góno simétrico de 12 con forma de hexágono más grande, que tiene pares adyacentes de bordes colineales.

Dos anticúpulas se pueden aumentar juntas sobre su base como una bianticupola.

Familia de convex anticupolae
$n$	2	3	4	5	6...
Nombre	$s{2}$	$s{3}$	$s{4}$	$s{5}$	$s{6}$
Imagen	Digonal	Triangular	Plaza	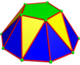Pentagonal	Hexagonal
Transparent
Net

Hypercupolae

El hipercupolae o cúpula poliedral son una familia de policora convexa no uniforme (aquí figuras cuatridimensionales), análoga a las cúpulas. Las bases de cada uno son un sólido platónico y su expansión.

Nombre	Tetraedral cupola		Cubic cupola		Octahedral Cupola		Dodecahedral Cupola		Tazón de azulejos hexagonales
Símbolo Schläfli	${3,3}$		${4,3}$		${3,4}$		${5,3}$		${6,3}$
Segmentochora índice	K4.23		K4.71		K4.107		K4.152
circunradius	${displaystyle 1}$		${fnMicroc} {3+{sqrt {2}{2}}approx 1.485634}$		${fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {cHFF}fnMicrosoft {fnMicrosoft {fnMicrosoft}fnMicrosoft {\fnMicrosoft {\fnMicrosoft {fnMicrosoft {fnMicrosoft}\\fnMicrosoft}\\\\fnMicrosoft\\\\fnMicrosoft\\\\fnMicrosoft\\\\\\\\\\\\\\\\\\\\\\\fnMicrosoft\\\\fnMicrosoft\\\fnMicrosoft\\\\\\\\\\\fnMicro {2+{sqrt {2}}approx 1.847759}$		${textstyle 3+{sqrt {5}approx 5.236068}$
Imagen
Células
Vertices	16		32		30		80		JUEGO
Edges	42		84		84		210		JUEGO
Caras	42	24 triángulos 18 plazas	80	32 triángulos 48 plazas	82	40 triángulos 42 plazas	194	80 triángulos 90 plazas 24 pentagones	JUEGO
Celdas	16	1 tetraedro 4 prismas triangulares 6 prismas triangulares 4 pirámides triangulares 1 cuboctaedro	28	1 cubo 6 prismas cuadrados 12 prismas triangulares 8 pirámides triangulares 1 rhombicuboctahedron	28	1 octaedro 8 prismas triangulares 12 prismas triangulares 6 pirámides cuadradas 1 rhombicuboctahedron	64	1 dodecahedron 12 prismas pentagonales 30 prismas triangulares 20 pirámides triangulares 1 rhombicosidodecahedron	JUEGO	1 nivel hexagonal prismas hexagonales prismas triangulares pirámides triangulares 1 baldosa rhombitrihexagonal
Relacionados uniforme polichora	5 celdas		tesseract		24 celdas		de 120 células		baldosas hexagonales correcinadas

Más resultados...