Cuboctaedro truncado

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Arquitecto sólido en geometría

Cuboctaedro truncado
(Haga clic aquí para el modelo giratorio)
Tipo	Arquitecto sólido Uniform polyhedron
Elementos	F = 26, E = 72, V = 48 (χ = 2)
Caras por lados	12{4}+8{6}+6{8}
Notación de Conway	b C o taC
Símbolos de Schläfli	tr{4,3} or $t{begin{Bmatrix}4\3end{Bmatrix}}$
Símbolos de Schläfli	t_0,1,2{4,3}
Signatura Wythoff	2 3 4 Silencio
Coxeter diagrama
Grupo de Symmetry	Oh, B₃, [4,3], (*432), orden 48
Grupo de rotación	O, [4,3]⁺, (432), orden 24
Ángulo Dihedral	4-6: arccos(−√6/3) = 144°44′08′ 4-8: arccos(−1/√2= 135° 6-8: arccos(−√3/3) = 125°15′51′
Referencias	U₁₁, C₂₃, W₁₅
Propiedades	Convexo semiregular zonohedron
Caras de colores	4.6.8 (Vertex figure)
Disdyakis dodecahedron (poliedro dual)	Cifras netas

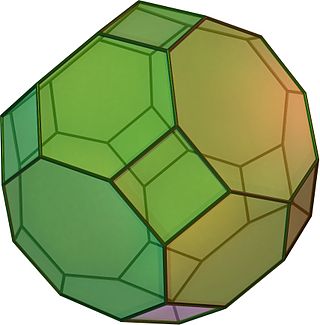
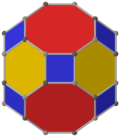
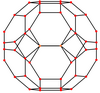
En geometría, el cuboctaedro truncado es un sólido de Arquímedes, denominado por Kepler como el truncamiento de un cuboctaedro. Tiene 12 caras cuadradas, 8 caras hexagonales regulares, 6 caras octogonales regulares, 48 vértices y 72 aristas. Dado que cada una de sus caras tiene simetría puntual (equivalente a una simetría rotacional de 180°), el cuboctaedro truncado es un 9-zonoedro. El cuboctaedro truncado puede teselar con el prisma octagonal.

Nombres

El nombre truncated cuboctahedron, dado originalmente por Johannes Kepler, es engañoso: una truncación real de un cuboctaedro tiene rectángulos en lugar de cuadrados; sin embargo, este poliedro no uniforme es topológicamente equivalente al sólido arquimediano sinrigoroso llamado cuboctaedro truncado.

Los nombres intercambiables alternativos son:

Cuboctaedro truncado (Johannes Kepler),
Rhombitruncated cuboctahedron (Magnus Wenninger),
Gran rhombicuboctaedron (Robert Williams),
Great rhombcuboctahedron (Peter Cromwell),
Cubo Omnitruncado o cubo cantitruncado (Norman Johnson),
Cubo bisturí (Notación de poliedro de Conway).

Cuboctahedron y su truncación

Hay un poliedro uniforme no convexo con un nombre similar: el gran rombicuboctaedro no convexo.

Coordenadas cartesianas

Las coordenadas cartesianas de los vértices de un cuboctaedro truncado con arista de longitud 2 y centrado en el origen son todas las permutaciones de:

(±1, ±(1 +)√2), ±(1 + 2√2)).

Área y volumen

El área A y el volumen V del cuboctaedro truncado de longitud de arista a son:

{displaystyle {begin{aligned}A&=12left(2+{sqrt {2}}+{sqrt {3}}right)a^{2}&&approx 61.755,1724~a^{2},\V&=left(22+14{sqrt {2}}right)a^{3}&&approx 41.798,9899~a^{3}.end{aligned}}}

Disección

El cuboctaedro truncado es el casco convexo de un rombicuboctaedro con cubos sobre sus 12 cuadrados en ejes de simetría doble. El resto de su espacio se puede dividir en 6 cúpulas cuadradas debajo de los octágonos y 8 cúpulas triangulares debajo de los hexágonos.

Un cuboctaedro truncado disecado puede crear un toroide de Stewart de género 5, 7 u 11 quitando el rombicuboctaedro central y las 6 cúpulas cuadradas, las 8 cúpulas triangulares o los 12 cubos, respectivamente. También se pueden construir muchos otros toroides de simetría inferior eliminando el rombicuboctaedro central y un subconjunto de los otros componentes de disección. Por ejemplo, quitar 4 de las cúpulas triangulares crea un toroide de género 3; si estas cúpulas se eligen apropiadamente, entonces este toroide tiene simetría tetraédrica.

Stewart toroids
Género 3	Género 5	Género 7	Genus 11

Colores uniformes

Solo hay una coloración uniforme de las caras de este poliedro, un color para cada tipo de cara.

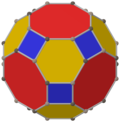
Existe una coloración uniforme de 2, con simetría tetraédrica, con hexágonos de colores alternos.

Proyecciones ortogonales

El cuboctaedro truncado tiene dos proyecciones ortogonales especiales en los planos A₂ y B₂ de Coxeter con [6] y [8] simetría proyectiva, y numerosas [2] las simetrías se pueden construir a partir de varios planos proyectados en relación con los elementos del poliedro.

Proyecciones ortogonales
Centrado por	Vertex	Edge 4-6	Edge 4-8	Edge 6-8	Cara normal 4-6
Imagen
Projective simetría	[2]⁺	[2]	[2]	[2]	[2]
Centrado por	Cara normal Plaza	Cara normal Octagon	Cara Plaza	Cara Hexagon	Cara Octagon
Imagen
Projective simetría	[2]	[2]	[2]	[6]	[4]

Alicatados esféricos

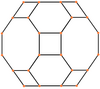
El cuboctaedro truncado también puede representarse como un mosaico esférico y proyectarse en el plano a través de una proyección estereográfica. Esta proyección es conforme, preservando ángulos pero no áreas o longitudes. Las líneas rectas sobre la esfera se proyectan como arcos circulares sobre el plano.

Proyección ortogonal	cuadrado centrado	hexágono centrado	octagonista

Proyección ortogonal	Proyecciones estereográficas

Grupo octaédrico completo

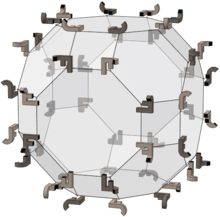
Como muchos otros sólidos, el octaedro truncado tiene una simetría octaédrica completa, pero su relación con el grupo octaédrico completo es más estrecha que eso: sus 48 vértices corresponden a los elementos del grupo, y cada cara de su dual es un dominio fundamental de el grupo.

La imagen de la derecha muestra las 48 permutaciones del grupo aplicadas a un objeto de ejemplo (a saber, el compuesto JF ligero de la izquierda). Los 24 elementos claros son rotaciones y los oscuros son sus reflejos.

Los bordes del sólido corresponden a los 9 reflejos del grupo:

Aquellos entre octógonos y plazas corresponden a las 3 reflexiones entre octógonos opuestos.
Los bordes hexagonales corresponden a las 6 reflexiones entre cuadrados opuestos.
(No hay reflexiones entre hexágonos opuestos.)

Los subgrupos corresponden a sólidos que comparten los respectivos vértices del octaedro truncado.
P.ej. los 3 subgrupos con 24 elementos corresponden a un cubo romo no uniforme con simetría octaédrica quiral, un rombicuboctaedro no uniforme con simetría piritoédrica (el octaedro romo cántico) y un octaedro truncado no uniforme con simetría tetraédrica completa. El subgrupo único con 12 elementos es el grupo alterno A₄. Corresponde a un icosaedro no uniforme con simetría tetraédrica quiral.

Subgrupos y sólidos correspondientes
Cuboctaedro truncado tr{4,3}	Snub cube sr{4,3}	Rhombicuboctahedron s₂{3,4}	Truncado octaedro h_1,2{4,3}	Icosahedron
[4,3] Full octahedral	[4,3]⁺ Chiral octaedral	[4,3]⁺] Pyritohedral	[1]⁺,4,3] = [3,3] Tetraedral completo	[1]⁺,4,3⁺] = [3,3]⁺ Chiral tetrahedral

todos 48 vértices	24 vértices			12 vértices

Poliedros relacionados


Bowtie tetrahedron y cubo contienen dos caras trapezoidales en lugar de cada cuadrado.

El cuboctaedro truncado pertenece a una familia de poliedros uniformes relacionados con el cubo y el octaedro regular.

Uniform octaedral polyhedra
Simetría: [4,3], (*432)							[4,3]⁺ (432)	[1]⁺,4,3] = [3,3] (*332)		[3]⁺,4] (3*2)
{4,3}	t{4,3}	r{4,3} r{3^1.1}	t{3,4} t{3^1.1}	{3,4} {3}^1.1}	rr{4,3} s₂{3,4}	tr{4,3}	sr{4,3}	h{4,3} {3,3}	h2{4,3} t{3,3}	S{3,4} s{3^1.1}

		=	=	=				= o	= o	=

Duals to uniform polyhedra
V43	V3.82	V(3.4)2	V4.62	V34	V3.43	V4.6.8	V34.4	V33	V3.62	V35

Este poliedro puede considerarse miembro de una secuencia de patrones uniformes con configuración de vértice (4.6.2p) y diagrama de Coxeter-Dynkin . Para pLos miembros de la secuencia son poliedros omnitruncados (zonohedrones), mostrados a continuación como revestimientos esféricos. Para pSe trata de revestimientos del plano hiperbólico, empezando por el revestimiento triheptagonal truncado.

n32 mutación de simetría de los revestimientos omnímicos: 4.6.2n* v t e
Sym. *n32 [n,3]	Spherical				Euclid.	Hiperb compacto.		Paraco.	Hiperbólico no consumado
Sym. *n32 [n,3]	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]	*∞32 [∞,3]	[12i,3]	[9i,3]	[6i,3]	[3i,3]
Gráficos
Config.	4.6.4	4.6.6	4.6.8	4.6.10	4.6.12	4.6.14	4.6.16	4.6.	4.6.24i	4.6.18i	4.6.12i	4.6.6i
Duales
Config.	V4.6.4	V4.6.6	V4.6.8	V4.6.10	V4.6.12	V4.6.14	V4.6.16	V4.6.	V4.6.24i	V4.6.18i	V4.6.12i	V4.6.6i

n42 mutación de simetría de los revestimientos omnímicos: 4.8.2n* v t e
Simmetría *n42 [n,4]	Spherical		Euclidean	Hiperbólico compacto				Paracomp.
Simmetría *n42 [n,4]	*242 [2,4]	*342 [3,4]	*442 [4,4]	*542 [5,4]	*642 [6,4]	*742 [7,4]	*842 [8,4]...	* [∞,4]
Omnitruncado gráfico	4.8.4	4.8.6	4.8.8	4.8.10	4.8.12	4.8.14	4.8.16	4.8.
Omnitruncado duales	V4.8.4	V4.8.6	V4.8.8	V4.8.10	V4.8.12	V4.8.14	V4.8.16	V4.8.

n32 mutación de simetría de los revestimientos omnímicos: 6.8.2n* v t e
Sym. *n43 [n,4,3)]	Spherical	Hiperbólico compacto						Paraco.
Sym. *n43 [n,4,3)]	*243 [4,3]	*343 [(3,4,3)]	*443 [4.43)]	*543 [(5,4,3)]	*643 [(6,4,3)]	*743 [(7,4,3)]	*843 [(8,4,3)]	*∞43 [(∞,4,3)]
Gráficos
Config.	4.8.6	6.8.6	8.8.6	10.8.6	12.8.6	14.8.6	16.8.6	∞.8.6
Duales
Config.	V4.8.6	V6.8.6	V8.8.6	V10.8.6	V12.8.6	V14.8.6	V16.8.6	V6.8.

Es el primero de una serie de hipercubos cantitruncados:

Proyecciones de polígono Petrie

Cuboctaedro truncado	Tesseract cantitruncado	Cantitruncado 5-cubo	Cantitruncado 6-cubo	Cantitruncado 7-cubo	Cantitruncado 8-cubo

Gráfico cuboctaédrico truncado

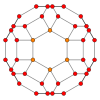
En el campo matemático de la teoría de grafos, un gráfico cuboctaédrico truncado (o gran gráfico rombocuboctaédrico) es el gráfico de vértices y aristas del cuboctaedro truncado, uno de los sólidos de Arquímedes. Tiene 48 vértices y 72 aristas, y es un grafo de Arquímedes cúbico y con simetría cero.

Contenido relacionado

Más resultados...