Cubo truncado

Cubo truncado
(Haga clic aquí para el modelo giratorio)
Tipo	Arquitecto sólido Uniform polyhedron
Elementos	F = 14, E = 36, V = 24 (χ = 2)
Caras por lados	8{3}+6{8}
Notación de Conway	tC
Símbolos de Schläfli	t{4,3}
	t0,1{4,3}
Signatura Wythoff	2 3 Silencio 4
Coxeter diagrama
Grupo de Symmetry	Oh, B3, [4,3], (*432), orden 48
Grupo de rotación	O, [4,3]+, (432), orden 24
Ángulo Dihedral	3-8: 125°15′51′′ 8-8: 90°
Referencias	U09, C21, W8
Propiedades	Convex semiregular
Caras de colores	3.8.8 (Vertex figure)
Triakis octahedron (poliedro dual)	Cifras netas

En geometría, el cubo truncado, o hexaedro truncado, es un sólido de Arquímedes. Tiene 14 caras regulares (6 octogonales y 8 triangulares), 36 aristas y 24 vértices.

Si el cubo truncado tiene una longitud de arista unitaria, su octaedro triakis dual tiene aristas de longitudes 2 y 2 + √2.

Área y volumen

El área A y el volumen V de un cubo truncado de longitud de arista a son:

A=2()6+62+3)a2.. 32.4346644a2V=21+1423a3.. 13.5996633a3.{displaystyle {begin{aligned}A paciente=2left(6+6{sqrt {2}+{sqrt {3}}right)a^{2} limitándoseapprox 32.434,6644a^{2}V dorm={21+14{sqrt} {2}} {3}a} {3} 13.599,6633a^{3}

Proyecciones ortogonales

El cubo truncado tiene cinco proyecciones ortogonales especiales, centradas, en un vértice, en dos tipos de aristas y dos tipos de caras: triángulos y octágonos. Los dos últimos corresponden a los planos B₂ y A₂ de Coxeter.

Proyecciones ortogonales

Centrado por	Vertex	Edge 3-8	Edge 8-8	Cara Octagon	Cara Triángulo
Sólido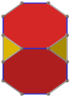
Wireframe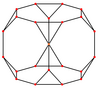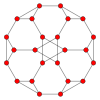
Doble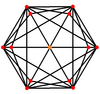
Projective simetría	[2]	[2]	[2]	[4]	[6]

Alicatados esféricos

El cubo truncado también se puede representar como un mosaico esférico y proyectarse en el plano a través de una proyección estereográfica. Esta proyección es conforme, preservando ángulos pero no áreas o longitudes. Las líneas rectas sobre la esfera se proyectan como arcos circulares sobre el plano.

	octagonista	triángulo centrado
Proyección ortográfica	Proyecciones estereográficas

Coordenadas cartesianas

Las coordenadas cartesianas para los vértices de un hexaedro truncado centrado en el origen con longitud de arista 2ξ son todas las permutaciones de

(±., ±1, ±1),

donde ξ = √2 − 1.

El parámetro ξ se puede variar entre ±1. Un valor de 1 produce un cubo, 0 produce un cuboctaedro y los valores negativos producen caras octagrámicas que se intersecan a sí mismas.

Si se eliminan las partes autointersecadas de los octagramas, dejando cuadrados y truncando los triángulos en hexágonos, se producen octaedros truncados y la secuencia termina con los cuadrados centrales reducidos a un punto y creando un octaedro.

Disección

El cubo truncado se puede dividir en un cubo central, con seis cúpulas cuadradas alrededor de cada una de las caras del cubo y 8 tetraedros regulares en las esquinas. Esta disección también se puede ver dentro del panal cúbico rúnico, con células de cubo, tetraedro y rombicuboctaedro.

Esta disección se puede usar para crear un toroide de Stewart con todas las caras regulares quitando dos cúpulas cuadradas y el cubo central. Este cubo excavado tiene 16 triángulos, 12 cuadrados y 4 octógonos.

Disposición de vértices

Comparte la disposición de vértices con tres poliedros uniformes no convexos:

Cubo truncado

Nonconvex gran rhombicuboctahedron

Great cubicuboctahedron

Gran rhombihexahedron

Poliedros relacionados

El cubo truncado se relaciona con otros poliedros y mosaicos en simetría.

El cubo truncado pertenece a una familia de poliedros uniformes relacionados con el cubo y el octaedro regular.

Uniform octaedral polyhedra
Simetría: [4,3], (*432)							[4,3]+ (432)	[1]+,4,3] = [3,3] (*332)		[3]+,4] (3*2)
{4,3}	t{4,3}	r{4,3} r{31.1}	t{3,4} t{31.1}	{3,4} {3}1.1}	rr{4,3} s2{3,4}	tr{4,3}	sr{4,3}	h{4,3} {3,3}	h2{4,3} t{3,3}	S{3,4} s{31.1}
		=	=	=				= o	= o	=
Duals to uniform polyhedra
V43	V3.82	V(3.4)2	V4.62	V34	V3.43	V4.6.8	V34.4	V33	V3.62	V35

Mutaciones de simetría

Este poliedro está relacionado topológicamente como parte de una secuencia de poliedros truncados uniformes con configuraciones de vértice (3.2n.2n) y [n,3] Simetría del grupo de Coxeter, y una serie de poliedros y teselaciones n.8.8.

*n32 mutación simetría de los revestimientos esféricos truncados: t{n,3}
Simmetría *n32 [n,3]	Spherical				Euclid.	Hiperb compacto.		Paraco.
	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]
Truncado cifras
Signatura	t{2,3}	t{3,3}	t{4,3}	t{5,3}	t{6,3}	t{7,3}	t{8,3}	.
Triakis cifras
Config.	V3.4.4	V3.6.6	V3.8.8	V3.10.10	V3.12.12	V3.14.14	V3.16.16	V3. Testamento.

*n42 mutación de simetría de los revestimientos truncados: n.8 v t e
Simmetría *n42 [n,4]	Spherical		Euclidean	Hiperbólico compacto				Paracompactar
	*242 [2,4]	*342 [3,4]	*442 [4,4]	*542 [5,4]	*642 [6,4]	*742 [7,4]	*842 [8,4]...	* [∞,4]
Truncado cifras
Config.	2.8.8	3.8.8	4.8.8	5.8.8	6.8.8	7.8.8	8.8.8	∞.8.8
N-kis cifras
Config.	V2.8.8	V3.8.8	V4.8.8	V5.8.8	V6.8.8	V7.8.8	V8.8.8	V∞.8.8

Alternator truncation

Tetraedro, su truncación de borde, y el cubo truncado

Al truncar los vértices alternos del cubo se obtiene el tetraedro biselado, es decir, la arista truncada del tetraedro.

El trapezoedro triangular truncado es otro poliedro que se puede formar a partir del truncamiento de la arista del cubo.

Polítopos relacionados

El cubo truncado, es el segundo en una secuencia de hipercubos truncados:

Hipercubos truncados

Imagen								...
Nombre	Octagon	Cubo truncado	Truncated tesseract	Truncado 5-cubo	Truncado 6-cubo	Truncado 7-cubo	Truncado 8-cubo
Coxeter diagrama
Vertex figure	()v()	()v{ }	()v{3}	()v{3,3}	()v{3,3,3}	()v{3,3,3,3,3}	()v{3,3,3,3,3,3}

Gráfico cúbico truncado

En el campo matemático de la teoría de grafos, un gráfico cúbico truncado es el gráfico de vértices y aristas del cubo truncado, uno de los sólidos de Arquímedes. Tiene 24 vértices y 36 aristas, y es un grafo de Arquímedes cúbico.

Ortográfico