Cubo

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Objeto sólido con seis caras cuadradas iguales

Hexahedron regular
(Haga clic aquí para el modelo giratorio)
Tipo	sólido platónico
Elementos	F = 6 E = 12 V = 8 (χ = 2)
Caras por lados	6{4}
Notación de Conway	C
Símbolos de Schläfli	{4,3}
Símbolos de Schläfli	t{2,4} o {4}×{} Tr{2,2} {fnK}fnK} {fnK}=}}}} {fnK}} {fn}} {fn}} {fn}}} {fn}}}fnK}}}} {fn}} {\fnK}} {f}}}}}}}}\\\\f}}}}}}}}}}}}}}}}}}}}}\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}³
Configuración facial	V3.3.3.3
Signatura Wythoff	3 Silencio 2 4
Coxeter diagrama
Simmetría	Oh, B₃, [4,3], (*432)
Grupo de rotación	O, [4,3]⁺, (432)
Referencias	U₀₆, C₁₈, W₃
Propiedades	regular, convexzonohedron, Hanner politope
Ángulo Dihedral	90°
4.4.4 (Vertex figure)	Octahedron (poliedro dual)
Cifras netas

Neta de un cubo

Modelo 3D de un cubo

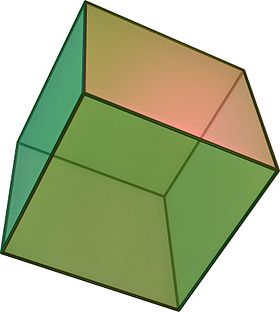
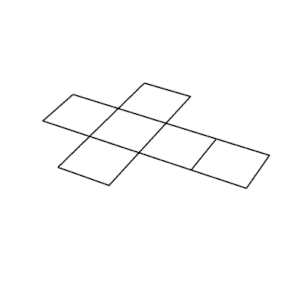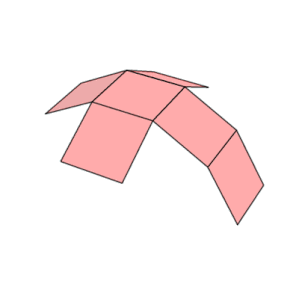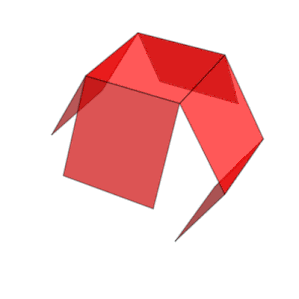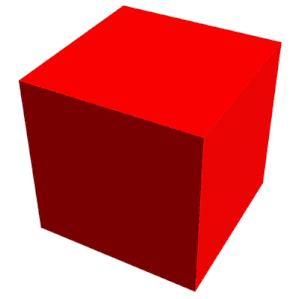
En geometría, un cubo es un objeto sólido tridimensional delimitado por seis caras, facetas o lados cuadrados, con tres encuentros en cada vértice. Visto desde una esquina, es un hexágono y su red suele representarse como una cruz.

El cubo es el único hexaedro regular y es uno de los cinco sólidos platónicos. Tiene 6 caras, 12 aristas y 8 vértices.

El cubo es también un paralelepípedo cuadrado, un paralelepípedo equilátero y un romboedro recto un 3-zonoedro. Es un prisma cuadrado regular en tres orientaciones y un trapezoedro trigonal en cuatro orientaciones.

El cubo es dual al octaedro. Tiene simetría cúbica u octaédrica.

El cubo es el único poliedro convexo cuyas caras son todas cuadradas.

Proyecciones ortogonales

El cubo tiene cuatro proyecciones ortogonales especiales, centradas, sobre un vértice, aristas, cara y normal a su vértice figura. El primero y el tercero corresponden a los planos A₂ y B₂ de Coxeter.

Proyecciones ortogonales
Centrado por	Cara	Vertex
Coxeter aviones	B₂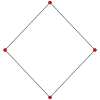	A₂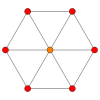
Projective simetría	[4]	[6]
Vistas frustradas

Alicatados esféricos

El cubo también se puede representar como un mosaico esférico y proyectarse en el plano a través de una proyección estereográfica. Esta proyección es conforme, preservando ángulos pero no áreas o longitudes. Las líneas rectas sobre la esfera se proyectan como arcos circulares sobre el plano.

Proyección ortográfica	Proyección estereográfica

Coordenadas cartesianas

Para un cubo con centro en el origen, con aristas paralelas a los ejes y con una longitud de arista de 2, las coordenadas cartesianas de los vértices son

(±1, ±1, ±1)

mientras que el interior consta de todos los puntos (x₀, x₁, x₂) con −1 < x_i < 1 para todos los i.

Ecuación en espacio tridimensional

En geometría analítica, la superficie de un cubo con centro (x₀, y₀, z₀) y la longitud de la arista de 2a es el lugar geométrico de todos los puntos (x, y , z) tal que

max{|x-x_{0}|,|y-y_{0}|,|z-z_{0}|}=a.

Un cubo también se puede considerar el caso límite de un superelipsoide 3D, ya que los tres exponentes se aproximan al infinito.

Fórmulas

Para un cubo de longitud de borde $a$ :

superficie	$6a^{2},$	volumen	$a^{3},$
cara diagonal	${sqrt {2}}a$	espacio diagonal	${textstyle {sqrt {3}}a}$
radio de esfera circunscrita	${frac {sqrt {3}}{2}}a$	radio de esfera tangente a bordes	${frac {a}{sqrt {2}}}$
radio de esfera inscrita	${frac {a}{2}}$	ángulos entre caras (en radians)	${frac {pi }{2}}$

Como el volumen de un cubo es el tercer poder de sus lados $atimes atimes a$ , terceros poderes se llaman cubos, por analogía con cuadrados y segundos poderes.

Un cubo tiene el volumen más grande entre los cuboides (cajas rectangulares) con un área de superficie dada. Además, un cubo tiene el mayor volumen entre los cuboides con el mismo tamaño lineal total (largo+ancho+alto).

Punto en el espacio

Para un cubo cuya esfera que lo circunscribe tiene radio R, y para un punto dado en su espacio tridimensional con distancias d_i desde los ocho vértices del cubo, tenemos:

{displaystyle {frac {sum _{i=1}^{8}d_{i}^{4}}{8}}+{frac {16R^{4}}{9}}=left({frac {sum _{i=1}^{8}d_{i}^{2}}{8}}+{frac {2R^{2}}{3}}right)^{2}.}

Duplicar el cubo

Doblar el cubo, o problema de Delian, era el problema planteado por los antiguos matemáticos griegos de usar solo un compás y una regla para comenzar con la longitud de la arista de un cubo dado y construir el longitud de la arista de un cubo con el doble del volumen del cubo original. No pudieron resolver este problema, que en 1837 Pierre Wantzel demostró que era imposible porque la raíz cúbica de 2 no es un número construible.

Colores uniformes y simetría

Árbol de simetría octadral

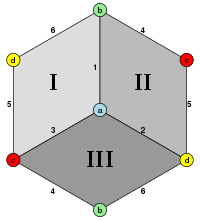
El cubo tiene tres colores uniformes, nombrados por los colores de las caras cuadradas alrededor de cada vértice: 111, 112, 123.

El cubo tiene cuatro clases de simetría, que se pueden representar coloreando las caras con vértices transitivos. La mayor simetría octaédrica O_h tiene todas las caras del mismo color. La simetría diédrica D_4h proviene de que el cubo es un sólido, con los seis lados de diferentes colores. Los subconjuntos prismáticos D_2d tienen la misma coloración que el anterior y D_2h tiene colores alternos para sus lados para un total de tres colores, emparejados por lados opuestos. Cada forma de simetría tiene un símbolo de Wythoff diferente.

Nombre	Recursos ordinarios hexahedron	Prisma cuadrada	Rectangular trapezoprismo	Rectangularcuboide	Rhombic prisma	Trigonal trapezohedron
Coxeterdiagram
Schläflisymbol	{4,3}	{4}×{} rr{4,2}	s₂{2,4}	{}³ Tr{2,2}	{}×2{}
Wythoffsymbol	3 Silencio 4 2	4 2 Silencio 2		2 2 2 Silencio
Simmetría	O_h [4,3] (*432)	D_4h [4,2] (*422)	D_2d [4,2]⁺] (2*2)	D_2h [2,2] (*222)		D_3d [6,2]⁺] (2*3)
Simmetría orden	24	16	8	8		12
Imagen (uniform para colorear)	(111)	(112)	(112)	(123)	(112)	(111), (112)

Relaciones geométricas

Las 11 redes del cubo.

Estos dados familiares de seis caras son en forma de cubo.

Un cubo tiene once redes (una de ellas se muestra arriba): es decir, hay once formas de aplanar un cubo hueco cortando siete aristas. Para colorear el cubo de modo que no haya dos caras adyacentes del mismo color, se necesitarían al menos tres colores.

El cubo es la celda del único mosaico regular del espacio euclidiano tridimensional. También es único entre los sólidos platónicos por tener caras con un número par de lados y, en consecuencia, es el único miembro de ese grupo que es un zonoedro (toda cara tiene simetría puntual).

El cubo se puede cortar en seis pirámides cuadradas idénticas. Si estas pirámides cuadradas se unen a las caras de un segundo cubo, se obtiene un dodecaedro rómbico (con pares de triángulos coplanares combinados en caras rómbicas).

En Teología

Los cubos aparecen en las religiones abrahámicas. La Kaaba en La Meca es un ejemplo que en árabe significa "el cubo". También aparecen en el judaísmo como Teffilin y la Nueva Jerusalén en el Nuevo Testamento también se describe como un Cubo.

Otras dimensiones

El análogo de un cubo en el espacio euclidiano de cuatro dimensiones tiene un nombre especial: un teseracto o hipercubo. Más correctamente, un hipercubo (o cubo n-dimensional o simplemente cubo n) es el análogo del cubo en el espacio euclidiano n-dimensional y un teseracto es el hipercubo de orden 4. Un hipercubo también se denomina politopo de medida.

También hay análogos del cubo en dimensiones inferiores: un punto en dimensión 0, un segmento de línea en una dimensión y un cuadrado en dos dimensiones.

Poliedros relacionados

El doble de un cubo es un octaedro, visto aquí con vértices en el centro de las caras cuadradas del cubo.

El hemicube es el cociente de 2 a 1 del cubo.

El cociente del cubo por el mapa antípoda produce un poliedro proyectivo, el hemicubo.

Si el cubo original tiene longitud de borde 1, su poliedro dual (un octaedro) tiene longitud de borde $scriptstyle {sqrt {2}}/2$ .

El cubo es un caso especial en varias clases de poliedros generales:

Nombre	¿Terceras iguales?	¿Angulos iguales?	¿Angulos rectos?
Cube	Sí.	Sí.	Sí.
Rhombohedron	Sí.	Sí.	No
Cuboid	No	Sí.	Sí.
Parallelepiped	No	Sí.	No
quadrilaterally faced hexahedron	No	No	No

Los vértices de un cubo se pueden agrupar en dos grupos de cuatro, formando cada uno un tetraedro regular; más generalmente, esto se conoce como un demicubo. Estos dos juntos forman un compuesto regular, la stella octangula. La intersección de los dos forma un octaedro regular. Las simetrías de un tetraedro regular corresponden a las de un cubo que asigna cada tetraedro a sí mismo; las otras simetrías del cubo mapean los dos entre sí.

Uno de estos tetraedros regulares tiene un volumen de 1/3 de la del cubo. El espacio restante consta de cuatro tetraedros irregulares iguales con un volumen de 1 //span>6 de la del cubo, cada uno.

El cubo rectificado es el cuboctaedro. Si se recortan las esquinas más pequeñas, obtenemos un poliedro con seis caras octogonales y ocho triangulares. En particular podemos obtener octágonos regulares (cubo truncado). El rombicuboctaedro se obtiene cortando las esquinas y los bordes en la cantidad correcta.

Un cubo se puede inscribir en un dodecaedro de modo que cada vértice del cubo sea un vértice del dodecaedro y cada arista sea una diagonal de una de las caras del dodecaedro; tomar todos esos cubos da lugar al compuesto regular de cinco cubos.

Si se truncan dos vértices opuestos de un cubo en la profundidad de los tres vértices conectados directamente a ellos, se obtiene un octaedro irregular. Ocho de estos octaedros irregulares se pueden unir a las caras triangulares de un octaedro regular para obtener el cuboctaedro.

El cubo está relacionado topológicamente con una serie de poliedros esféricos y mosaicos con figuras de vértice de orden 3.

*n32 mutación simetría de los revestimientos regulares: {}n,3} v t e
Spherical				Euclidean	Hiperb compacto.		Paraco.	Hiperbólico no consumado

{2,3}	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	- ¿Qué?	{12i,3}	{9i,3}	{6i,3}	{3i,3}

El cuboctaedro es uno de una familia de poliedros uniformes relacionados con el cubo y el octaedro regular.

Uniform octaedral polyhedra
Simetría: [4,3], (*432)							[4,3]⁺ (432)	[1]⁺,4,3] = [3,3] (*332)		[3]⁺,4] (3*2)
{4,3}	t{4,3}	r{4,3} r{3^1.1}	t{3,4} t{3^1.1}	{3,4} {3}^1.1}	rr{4,3} s₂{3,4}	tr{4,3}	sr{4,3}	h{4,3} {3,3}	h2{4,3} t{3,3}	S{3,4} s{3^1.1}

		=	=	=				= o	= o	=

Duals to uniform polyhedra
V43	V3.82	V(3.4)2	V4.62	V34	V3.43	V4.6.8	V34.4	V33	V3.62	V35

El cubo está relacionado topológicamente como parte de una secuencia de mosaicos regulares, que se extiende en el plano hiperbólico: {4,p}, p=3,4,5...

*n42 mutación simetría de los revestimientos regulares: 4.n} v t e
Spherical	Euclidean	Hiperbólico compacto				Paracompactar
{4,3}	{4,4}	{4,5}	{4,6}	{4,7}	{4,8}...	{4}

Con simetría diédrica, Dih₄, el cubo está relacionado topológicamente en una serie de poliedros uniformes y mosaicos 4.2n.2n, que se extienden en el plano hiperbólico:

*n42 mutación simetría de los revestimientos truncados: 4.2n.2n v t e
Simmetría *n42 [n,4]	Spherical		Euclidean	Hiperbólico compacto				Paracomp.
Simmetría *n42 [n,4]	*242 [2,4]	*342 [3,4]	*442 [4,4]	*542 [5,4]	*642 [6,4]	*742 [7,4]	*842 [8,4]...	* [∞,4]
Truncado cifras
Config.	4.4.4	4.6.6	4.8.8	4.10.10	4.12.12	4.14.14	4.16.16	4. Voluntad.
N-kis cifras
Config.	V4.4.4	V4.6.6	V4.8.8	V4.10	V4.12.12	V4.14.14	V4.16.16	V4.∞.

Todas estas figuras tienen simetría octaédrica.

El cubo es parte de una secuencia de poliedros rómbicos y mosaicos con [n,3] simetría de grupo de Coxeter. El cubo puede verse como un hexaedro rómbico donde los rombos son cuadrados.

Mutaciones de simetría de azulejos cuasiregulares duales: V(3.n)²
*n32	Spherical			Euclidean	Hiperbólico
*n32	*332	*432	*532	*632	*732	*832...	*∞32
Tiling
Conf.	V(3.3)2	V(3.4)2	V(3.5)2	V(3.6)2	V(3.7)2	V(3.8)2	V(3.∞)2

El cubo es un prisma cuadrado:

Familia de uniforme n- prismas gonales v t e
Nombre de Prism	Digo prismo	(Trigonal) Triangular prism	(Tetragonal) Prisma cuadrada	Prisma pentagonal	Prisma hexagonal	Prisma heptagonal	El prisma octogonal	Enneagonal prism	Prisma Decagonal	Prisma hendecagonal	El prisma dodecagonal	...	Prismo Apeirogonal
Imagen de poliedro												...
Imagen de revestimiento esférico												Imagen de azulado plano
Config de Vertex.	2.4.4	3.4.4	4.4.4	5.4.4	6.4.4	7.4.4	8.4.4	9.4.4	10.4.4	11.4.4	12.4.4	...	∞.4
Coxeter diagrama												...

Como trapezoedro trigonal, el cubo está relacionado con la familia de simetría diedro hexagonal.

Uniform hexagonal dihedral spherical polyhedra
Simetría: [6,2], (*622)							[6,2]⁺, (622)	[6,2]⁺], (2*3)


{6,2}	t{6,2}	r{6,2}	t{2,6}	{2,6}	rr{6,2}	tr{6,2}	sr{6,2}	S{2,6}
Duals to uniforms

V62	V122	V62	V4.4.6	V26	V4.4.6	V4.4.12	V3.3.3.6	V3.3.3.3

Compuestos regulares y uniformes de cubos
Compuesto de tres cubos	Compuesto de cinco cubos

En panales uniformes y policora

Es un elemento de 9 de 28 panales uniformes convexos:

Cubic honeycomb	Truncado panal prismático	Snub cuadrado panal prismático	Elongated triangular prismatic honeycomb	Gyroelongated triangular prismatic honeycomb

Cantellated cubic honeycomb	Cantitruncado de miel cúbica	Combustible de miel cúbica	Cobertura de miel cúbica alternada

También es un elemento de cinco policoras uniformes de cuatro dimensiones:

Tesseract	Cantellated 16-cell	Tesseract	Cantitruncado 16 celdas	Runcitruncated 16-cell

Gráfica cúbica

El esqueleto del cubo (los vértices y las aristas) forma un gráfico de 8 vértices y 12 aristas, llamado gráfico del cubo. Es un caso especial del gráfico de hipercubo. Es uno de los 5 gráficos platónicos, cada uno un esqueleto de su sólido platónico.

Una extensión es el gráfico tridimensional k-ARY Hamming, que para k = 2 es el gráfico del cubo. Los gráficos de este tipo aparecen en la teoría del procesamiento paralelo en las computadoras.

Contenido relacionado

Más resultados...