Cuaterniones y rotación espacial
Los cuaterniones unitarios, conocidos como versores, proporcionan una notación matemática conveniente para representar orientaciones espaciales y rotaciones de elementos en un espacio tridimensional. Específicamente, codifican información sobre una rotación de ángulo de eje sobre un eje arbitrario. Los cuaterniones de rotación y orientación tienen aplicaciones en gráficos por computadora, visión por computadora, robótica, navegación, dinámica molecular, dinámica de vuelo, mecánica orbital de satélites y análisis de textura cristalográfica.
Cuando se utiliza para representar la rotación, también se denominan cuaternones cuaternones de rotación como representan el grupo de rotación 3D. Cuando se utiliza para representar una orientación (rotación relativa a un sistema de coordenadas de referencia), se llaman quaternions de orientación o de la actitud. Una rotación espacial alrededor de un punto fijo Silencio Silencio {displaystyle theta } radia alrededor de un eje de unidad ()X,Y,Z){displaystyle (X,Y,Z)} que denota el Eje de Euler es dado por la cuaternión ()C,XS,YS,ZS){displaystyle (C,X,S,Y,S,Z,S)}, donde C=# ()Silencio Silencio /2){displaystyle C=cos(theta /2)} y S=pecado ()Silencio Silencio /2){displaystyle S=sin(theta /2)}.
En comparación con las matrices de rotación, las quaterniones son más compactas, eficientes y numéricamente estables. Comparados con los ángulos de Euler, son más simples de componer. Sin embargo, no son tan intuitivos y fáciles de entender y, debido a la naturaleza periódica del seno y el cosino, los ángulos de rotación que difieren precisamente por el período natural serán codificados en cuaternones idénticos y los ángulos recuperados en radians se limitarán a [0,2π π ]{displaystyle [0,2pi]}.
Usando cuaterniones como rotaciones
En el espacio tridimensional, según el teorema de rotación de Euler, cualquier rotación o secuencia de rotaciones de un cuerpo rígido o sistema de coordenadas sobre un punto fijo es equivalente a una sola rotación por un ángulo dado Silencio Silencio {displaystyle theta } sobre un eje fijo (llamado el Eje de EulerEso pasa por el punto fijo. El eje Euler normalmente está representado por un vector unitariou→ → {displaystyle {vec}} ()e^ ^ {displaystyle {hat {e}}} en la imagen). Por lo tanto, cualquier rotación en tres dimensiones puede ser representado como una combinación de un vectoru→ → {displaystyle {vec}} y un cuero cabelludo Silencio Silencio {displaystyle theta }.
Los cuaterniones brindan una manera simple de codificar esta representación eje-ángulo en cuatro números, y se pueden usar para aplicar (calcular) la rotación correspondiente a un vector de posición (x,y,z) , que representa un punto relativo al origen en R3.
Vectores euclidianos como (2, 3, 4) o (ax, ay, az) se puede reescribir como 2 i + 3 j + 4 k o ax i + ay j + az k, donde i, j, k son vectores unitarios que representan los tres ejes cartesianos (tradicionalmente x, y, z), y también obedecen las reglas de multiplicación de las unidades fundamentales del cuaternión.
Por lo tanto, una rotación de ángulo Silencio Silencio {displaystyle theta } alrededor del eje definido por el vector de unidad
- u→ → =()ux,uSí.,uz)=uxi+uSí.j+uzk{displaystyle {vec {u}=(u_{x},u_{y}=u_{x}mathbf {i} ¿Qué? ¿Qué?
puede representarse mediante un cuaternión. Esto se puede hacer usando una extensión de la fórmula de Euler:
- q=eSilencio Silencio 2()uxi+uSí.j+uzk)=# Silencio Silencio 2+()uxi+uSí.j+uzk)pecado Silencio Silencio 2{displaystyle mathbf {q} =e^{frac} {theta {fnMicrosoft Sans Serif} {fnMicrosoft} {f}} {f} {f}} {f} {f}}} {f}} {f}}}} {f}} {f}} {f}}} {f} {f}}} {f}}} {f}}}} {f}} {f} {f}}} {f}} {f}} {f}}}}}} {f}} {f} {f} {f} {f} {f}}}}}}}}} {f} {f} {f} {f} {f} {f} {f} {f}}}}}}}}}}}}}}}}}f} {f} {f} {f}}f}}}}}}}}}}}}}}}}}}}}}}}}}}}} {i} {fnK}=cos {thetat} } {2}+(u_{x}mathbf {i} ¿Qué? } {2}}
Se puede demostrar que la rotación deseada se puede aplicar a un vector ordinario p=()px,pSí.,pz)=pxi+pSí.j+pzk{displaystyle mathbf {p} =(p_{x},p_{y},p_{z}=p_{x}mathbf {i} Mathbf. en espacio tridimensional, considerado como una cuaternión con una verdadera coordinación igual a cero, evaluando la conjugación dep porq se define como:
- p.=qpq− − 1{displaystyle mathbf {p} =mathbf {q} {fn}
utilizando el producto de Hamilton, donde p′ = (px′, p y′, pz′) es el nuevo vector de posición del punto después de la rotación. En una implementación programática, la conjugación se logra mediante la construcción de un cuaternión cuya parte vectorial es p y la parte real es igual a cero, y luego se realiza la multiplicación del cuaternión. La parte vectorial del cuaternión resultante es el vector deseado p′.
Un hecho geométrico independiente de las cuaterniones es la existencia de un mapeo de dos a uno de las rotaciones físicas a matrices de transformación rotacional. Si Silencio Silencio {displaystyle theta } ⩽ 2π π {displaystyle 2pi}, una rotación física sobre u→ → {displaystyle {vec}} por Silencio Silencio {displaystyle theta } y una rotación física − − u→ → {displaystyle - {vec}} por 2π π − − Silencio Silencio {displaystyle 2pi -theta } ambos logran la misma orientación final por caminos descomunales a través de orientaciones intermedias. Al insertar esos vectores y ángulos en la fórmula para q arriba, uno encuentra que si q representa la primera rotación, -q representa la segunda rotación. Esta es una prueba geométrica de conjugación q y por −q debe producir la misma matriz de transformación rotacional. Ese hecho se confirma algebraicamente notando que la conjugación es cuadrática en q, así que la señal de q cancela, y no afecta el resultado. (Véase 2:1 cartografía de SU(2) a SO(3)) Si ambas rotaciones son de media vuelta ()Silencio Silencio =π π ){displaystyle (theta =pi)}, ambos q y -q tendrá una coordinación real igual a cero. De lo contrario, uno tendrá una parte real positiva, representando una rotación por un ángulo inferior a π π {displaystyle pi}, y el otro tendrá una parte real negativa, representando una rotación por un ángulo mayor que π π {displaystyle pi}.
Matemáticamente, esta operación lleva el conjunto de todos los "puros" cuaterniones p (aquellos con parte real igual a cero)—que constituyen un espacio tridimensional entre los cuaterniones—en sí mismo, mediante la rotación deseada sobre el eje u, por el ángulo θ. (Cada cuaternión real se introduce en sí mismo mediante esta operación. Pero para el propósito de las rotaciones en el espacio tridimensional, ignoramos los cuaterniones reales).
La rotación es de reloj si nuestra línea de puntos de vista en la misma dirección que u→ → {displaystyle {vec}}.
En esta instancia (¿cuál?), q es un cuaternión unitario y
- q− − 1=e− − Silencio Silencio 2()uxi+uSí.j+uzk)=# Silencio Silencio 2− − ()uxi+uSí.j+uzk)pecado Silencio Silencio 2.{displaystyle mathbf {q} ^{-1}=e^{-{frac {theta {fnMicrosoft Sans Serif} {fnMicrosoft} {f}} {f} {f}} {f} {f}}} {f}} {f}}}} {f}} {f}} {f}}} {f} {f}}} {f}}} {f}}}} {f}} {f} {f}}} {f}} {f}} {f}}}}}} {f}} {f} {f} {f} {f} {f}}}}}}}}} {f} {f} {f} {f} {f} {f} {f} {f}}}}}}}}}}}}}}}}}f} {f} {f} {f}}f}}}}}}}}}}}}}}}}}}}}}}}}}}}} {i} {fnK}=cos {thetat} } {2}-(u_{x}mathbf {i} ¿Qué? } {2}}.
Se sigue que la conjugación por el producto de dos cuaterniones es la composición de conjugaciones por estos cuaterniones: Si p y q son cuaterniones unitarios, entonces la rotación (conjugación) por pq es
- pqv→ → ()pq)− − 1=pqv→ → q− − 1p− − 1=p()qv→ → q− − 1)p− − 1{fnMicrosoft} {f} {f}} {f}} {f}} {f}} {f} {}} {f}} {}} {f}} {f} {f}f} {f}}} {f} {f}} {f}}} {f}f}}}} {f}f}}}}}}}}}} {f}}}} {f}}f}}}}}}}} {f} {f}}}} {f}f}}}}}}}}}f}}}}}}}}}} {f}}}} {f} {f}}}}} {f}}}} {f}}} {f}}}}}f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}},
que es lo mismo que rotar (conjugar) por q y luego por p. La componente escalar del resultado es necesariamente cero.
La cuaternión inversa de una rotación es la rotación opuesta, ya que q− − 1()qv→ → q− − 1)q=v→ → {displaystyle mathbf {q} {f} {f} {f} {f}mhbf {f} {f})mthbf {q} = {f} {f}f} {f}} {f}}}}. El cuadrado de una rotación de cuaternión es una rotación en el doble del ángulo alrededor del mismo eje. Más generalmente qn es una rotación porn veces el ángulo alrededor del mismo eje que q. Esto se puede ampliar a la realidad arbitraria n, permitiendo una interpolación suave entre las orientaciones espaciales; véase Slerp.
Dos cuaterniones de rotación se pueden combinar en un cuaternión equivalente mediante la relación:
- q.=q2q1{displaystyle mathbf {q}=mathbf {q} ¿Qué? ¿Qué?
donde q′ corresponde a la rotación q1 seguido de la rotación q2. Por lo tanto, se puede componer un número arbitrario de rotaciones juntas y luego aplicarlas como una sola rotación. (Tenga en cuenta que la multiplicación de cuaterniones no es conmutativa).
Ejemplo de operación de conjugación
Conjugar p por q se refiere a la operación p ↦ qpq−1.
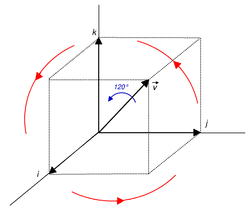
Considere la rotación f alrededor del eje v→ → =i+j+k{displaystyle {vec}=mathbf {i} +mathbf {j} # Mathbf {k}, con un ángulo de rotación de 120°, o 2π/3radians.
- α α =2π π 3{displaystyle alpha ={frac {2pi } {3}}
La longitud v→ → {displaystyle {vec}} es √3, el ángulo medio es π/3 (60°) con cosina 1/2, (porque 60° = 0,5) y pecado √3/2, (sin 60° ♥ 0.866). Por lo tanto, estamos tratando con una conjugación por la cuaternión unidad
- u=# α α 2+pecado α α 2⋅ ⋅ 1.. v→ → .. v→ → =# π π 3+pecado π π 3⋅ ⋅ 13v→ → =12+32⋅ ⋅ 13v→ → =12+32⋅ ⋅ i+j+k3=1+i+j+k2{displaystyle {begin{aligned}u ventaja=cos {frac {alpha ################################################################################################################################################################################################################################################################ } {2}cdot {frac {1}{fncipado {fnMic} {fn}fn} {fnK} {fnK}}}} {fnMicrosoft}} {fn}} {fn}}}} {fn}}}}fn}}}}fnfn}}} {\fnf}}}}fnfnfnfnfnfnh}}}}}}}}}}}}\\fnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfn}}}fn\\fnfnfnfnfnfn}}fn}}fnh}}}}fnfn\fnh}}}}}} {fnK}\fnK}\fnK}f}\\fncH00}\fn}\fnc}\fn}\fn\cH0}\fn\cccH0cccH00}\cH0ccH3cH0cH3cH0cH0cH3cH3cH3cH00}\cH00}\\cH0cH00}cH3cc\\ccccccccccccH3ccccc\cc\\cH3ccH3\\\cccH3\cH3c\cH3\\cH3\\cccH ################################################################################################################################################################################################################################################################ } {3}cdot {frac {1}{sqrt {}}{vec {fn}\fn}\fnh}\fnh}\\fn}\\fn}}\\fn}\fn}\fn}}\\fn}\fn}\fn}\\fn}}\\\\fn}\\fn}\\\fn}\\fn}\fn}\\\fn}\\fn}}\\\\\\\\\\\\\fn}fn}fn}fn}\\\fn}\\fn}\fn}fn}\fn}fn}\\\\\\fn}\\fn {1}{2}}+{frac {sqrt {3}{2}cdot {frac} {1}{sqrt {}}{vec {fn}\fn}\fnh}\fnh}\\fn}\\fn}}\\fn}\fn}\fn}}\\fn}\fn}\fn}\\fn}}\\\\fn}\\fn}\\\fn}\\fn}\fn}\\\fn}\\fn}}\\\\\\\\\\\\\fn}fn}fn}fn}\\\fn}\\fn}\fn}fn}\fn}fn}\\\\\\fn}\\fn {2} {fn}}cdot {fnh}cdot {fnMitbf {}} {c}} {cdot {f} {fn} {fnK} {f}} {c}} {cdot {c}} {c}}}}cdot {f}}}}cdot}cdot {cdot {cdot {cdot {cdot {f} {f} {f}f} {cdot {f} {f}f}f}f}f}f}f}f}f}f}f}f}f} {f}f}f}f} {f}f}f}f}f}f}fn}fn}f}f}fn}f}f}f}f}c} +mathbf {j} +mathbf {k} {fnMitbf {}}\fnMic {1+fnMitbf} +mathbf {j} +mathbf {k} } {2}end{aligned}}
Si f es la función de rotación,
- f()ai+bj+ck)=u()ai+bj+ck)u− − 1{displaystyle f(amathbf {i} +bmathbf {j} - Sí. - Sí.
Se puede demostrar que el inverso de un cuaternión unitario se obtiene simplemente cambiando el signo de sus componentes imaginarias. Como consecuencia,
- u− − 1=1− − i− − j− − k2{displaystyle u^{-1}={dfrac {1-Mathbf {i} - Mathbf {j} - Mathbf {k} } {2}}
y
- f()ai+bj+ck)=1+i+j+k2()ai+bj+ck)1− − i− − j− − k2{displaystyle f(amathbf {i} +bmathbf {j} +cmathbf {k}={dfrac {1+Mathbf {i} +mathbf {j} ¿Qué? +bmathbf {j} - ¿Qué? {1-Mathbf {i} - Mathbf {j} - Mathbf {k} } {2}}
Esto se puede simplificar, usando las reglas ordinarias para la aritmética de cuaterniones, para
- f()ai+bj+ck)=ci+aj+bk{displaystyle f(amathbf {i} +bmathbf {j} - Sí. +amathbf {j} - No.
Como era de esperar, la rotación corresponde a mantener un cubo fijo en un punto y rotarlo 120° sobre la diagonal larga a través del punto fijo (observe cómo los tres ejes se permutan cíclicamente).
Matriz de rotación derivada de cuaterniones
Una rotación de quaternion p.=qpq− − 1{displaystyle mathbf {p} =mathbf {q} {fn} (con q=qr+qii+qjj+qkk{displaystyle mathbf {q} =q_{r}+q_{i}mathbf {i} ¿Qué? ¿Qué?) puede ser manipulado algebraicamente en una rotación de matriz p.=Rp{displaystyle mathbf {p} =mathbf {Rp}, donde R{displaystyle mathbf {R} es la matriz de rotación dada por:
- R=[1− − 2s()qj2+qk2)2s()qiqj− − qkqr)2s()qiqk+qjqr)2s()qiqj+qkqr)1− − 2s()qi2+qk2)2s()qjqk− − qiqr)2s()qiqk− − qjqr)2s()qjqk+qiqr)1− − 2s()qi2+qj2)]{displaystyle mathbf {cH00} {cH00} {cH00} {cH00}} {cH00}} {cH00}} {ccH00} {cH00} {cH00} {cH00} {cH00}} {cH00} {cH00}}cH00} {cH00}}} {ccH00}}}} {ccccccH00}}ccc}}}}}}}}}} {ccccccH00}ccccccccccccccccH00}}cccH00}}}cH00}cH00}}cH00}}}cH00}}cccccH00}ccH00}}}}}}}}
Aquí. s=.. q.. − − 2{displaystyle s= 'Principal' y si q es un cuarto de unidad, s=1− − 2=1{displaystyle S=1^{-2}=1}.
Esto se puede obtener utilizando cálculo vectorial y álgebra lineal si expresamos p{displaystyle mathbf {p} y q{displaystyle mathbf {q} como partes de escalar y vector y utilizar la fórmula para la operación de multiplicación en la ecuación p.=qpq− − 1{displaystyle mathbf {p} =mathbf {q} {fn}. Si escribimos p{displaystyle mathbf {p} como ()0,p){displaystyle left(0,Mathbf {p} right)}, p.{displaystyle mathbf {p} como ()0,p.){displaystyle left(0,Mathbf {p}right)} y q{displaystyle mathbf {q} como ()qr,v){displaystyle left(q_{r},mathbf {v} right)}, donde v=()qi,qj,qk){displaystyle mathbf {v} =left(q_{i},q_{j},q_{k}right)}, nuestra ecuación se convierte en ()0,p.)=()qr,v)()0,p)s()qr,− − v){displaystyle left(0,mathbf {p} 'right)=left(q_{r},\mathbf {v} right)left(0,mathbf {p}left(q_{r}, -mathbf {v} right)}}}}. Mediante el uso de la fórmula para la multiplicación de dos quaternions que se expresan como partes escalar y vectoriales,
- ()r1,v→ → 1)()r2,v→ → 2)=()r1r2− − v→ → 1⋅ ⋅ v→ → 2,r1v→ → 2+r2v→ → 1+v→ → 1× × v→ → 2),{displaystyle left(r_{1}, {vec {v}_{1}right)left(r_{2}, {vec {v}_{2}right)=left(r_{1}r_{2}-{vec} {}_{1}cdot {vec}_{2}, r_{1}{vec} {vec} {fnMicrosoft} {fnMicrosoft} {fnMicrosoft} {fn}}} {fn}}}} {fn}} {fn}} {fn}}}}fnfn}}}\\fn}}}\\fn}}}\fn}}}}}\\\\fn}}}}}}}\\\\\\\c}}}}}}}}}}\\\\\\c}}}}}}}}}}}\\\\\\\\\\\\\c}}}}}}}}}}}\\\\\\\\c}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {fnK} {fnh}fnh}\fnh}fnfnfnh}\fn} {fnMicrosoft Sans Serif}
esta ecuación se puede reescribir como
- ()0,p.)=()()qr,v)()0,p))s()qr,− − v)=()qr0− − v⋅ ⋅ p,qrp+0v+v× × p)s()qr,− − v)=s()− − v⋅ ⋅ p,qrp+v× × p)()qr,− − v)=s()− − v⋅ ⋅ pqr− − ()qrp+v× × p)⋅ ⋅ ()− − v),()− − v⋅ ⋅ p)()− − v)+qr()qrp+v× × p)+()qrp+v× × p)× × ()− − v))=s()− − v⋅ ⋅ pqr+qrv⋅ ⋅ p,v()v⋅ ⋅ p)+qr2p+qrv× × p+v× × ()qrp+v× × p))=()0,s()v⊗ ⊗ v+qr2I+2qr[v]× × +[v]× × 2)p),{f} {f} {f} q_{r}+q_{r}mathbf {v} cdot mathbf {p} mathbf {v} left(mathbf {v} cdot mathbf {p}right)+q_{r} {2}mathbf {p} +q_{r}mathbf} +mathbf {v} times left(q_{r}mathbf {p} +mathbf {v} times mathbf {p}right)= ventajaleft(0, sleft(mathbf {v} otimes mathbf {v} #### ############################################################################################################################################################################################################################################################ {I} +2q_{r}[mathbf {v}_{times }+[mathbf {v}_{times }{2}right)mathbf {p}right),end{aligned}}}}
Donde ⊗ ⊗ {displaystyle otimes } denota el producto exterior, I{displaystyle mathbf {I} es la matriz de identidad y [v]× × {displaystyle [Mathbf {v]_{times } es la matriz de transformación que cuando se multiplica de la derecha con un vector u{displaystyle mathbf {u} da el producto de la cruz v× × u{displaystyle mathbf {v} times mathbf {u}.
Desde p.=Rp{displaystyle mathbf {=Mathbf {R} mathbf {p}, podemos identificar R{displaystyle mathbf {R} como s()v⊗ ⊗ v+qr2I+2qr[v]× × +[v]× × 2){displaystyle sleft(mathbf {v} otimes mathbf {v} #### ############################################################################################################################################################################################################################################################ [I} +2q_{r} [mathbf {v}_{times }+[mathbf {v}_{times }{2}right)}, que después de la expansión debe dar lugar a la expresión escrita en forma de matriz anterior.
Recuperando la representación eje-ángulo
La expresión qpq− − 1{displaystyle mathbf {q} mathbf {p} mathbf {q} ^{-1} rota cualquier cuaternión vectorial p{displaystyle mathbf {p} alrededor de un eje dado por el vector a{displaystyle mathbf {a} por el ángulo Silencio Silencio {displaystyle theta }, donde a{displaystyle mathbf {a} y Silencio Silencio {displaystyle theta } depende de la cuaternión q=qr+qii+qjj+qkk{displaystyle mathbf {q} =q_{r}+q_{i}mathbf {i} ¿Qué? ¿Qué?.
a{displaystyle mathbf {a} y Silencio Silencio {displaystyle theta } se puede encontrar en las siguientes ecuaciones:
- ()ax,aSí.,az)=()qi,qj,qk)qi2+qj2+qk2Silencio Silencio =2atan2()qi2+qj2+qk2,qr),{displaystyle {begin{aligned}(a_{x},a_{y},a_{z}={}{frac {q_{i},q_{j},q_{k}}{sq} {sqrt}} {sq_{i} {q_{i}}[2pt]theta =2operatorname {atan2} &left({sqrt)}[2pt]theta =2operatorname {atan2} {q_{i}{2}}}},q_{j}} {c}}},q_{r}derecho),end{aligned}}}
Donde atan2{displaystyle operatorname {atan2} es el arctante de dos brazos.
Se debe tener cuidado cuando el cuaternión se acerca a un escalar, ya que debido a la degeneración, el eje de una rotación de identidad no está bien definido.
La composición de las rotaciones espaciales
Un beneficio de la formulación de cuaterniones de la composición de dos rotaciones RB y RA es que produce directamente el eje de rotación y el ángulo de la rotación compuesta RC = RBRA.
Dejar la cuaternión asociada a una rotación espacial R se construye a partir de su eje de rotación S con el ángulo de rotación φ φ {displaystyle varphi } alrededor de este eje. La cuaternión asociada es dada por
Ampliar este producto para obtener
Divida ambos lados de esta ecuación por la identidad, que es la ley de los cosenos en una esfera,
Soy Rodrigues' fórmula para el eje de una rotación compuesta definida en términos de los ejes de las dos rotaciones. Derivó esta fórmula en 1840 (ver página 408).
Los tres ejes de rotación A, B y C forman un triángulo esférico y los ángulos diedros entre los planos formados por los lados de este triángulo están definidos por los ángulos de rotación. Hamilton presentó la forma de componentes de estas ecuaciones mostrando que el producto de cuaterniones calcula el tercer vértice de un triángulo esférico a partir de dos vértices dados y sus longitudes de arco asociadas, lo que también define un álgebra para puntos en geometría elíptica.
Composición eje-ángulo
El eje de rotación normalizado, eliminando el # γ γ 2{textstyle cos {frac {gamma } {2}} del producto expandido, deja el vector que es el eje de rotación, veces algo constante. Cuidado debe tomarse normalizando el vector del eje cuando γ γ {displaystyle gamma } es 0{displaystyle 0} o k2π π {displaystyle k2pi} donde el vector está cerca 0{displaystyle 0}; que es identidad, o 0 rotación alrededor de cualquier eje.
O con sustituciones trigonométricas de suma de ángulos...
finalmente normalizar el eje de rotación: D2pecado 12γ γ {textstyle {frac {fnMicrosoft} {}{2sin {fnMicroc} {1}{2}gamma } o D.. D.. {fnMicroc {fnK} {fnMitbf} {fnMicrosoft} {f}} {f}fnMitbf} {}}.
Diferenciación con respecto al cuaternión de rotación
El cuaternión rotado p' = q p q−1 debe diferenciarse con respecto al cuaternión giratorio q, cuando la rotación se estima a partir de la optimización numérica. La estimación del ángulo de rotación es un procedimiento esencial en el registro de objetos 3D o la calibración de cámaras. Para q unitario y p imaginario puro, es decir, para un rotación en el espacio 3D, las derivadas del cuaternión rotado se pueden representar usando notación de cálculo matricial como
- ∂ ∂ p.∂ ∂ q↑ ↑ [∂ ∂ p.∂ ∂ q0,∂ ∂ p.∂ ∂ qx,∂ ∂ p.∂ ∂ qSí.,∂ ∂ p.∂ ∂ qz]=[pq− − ()pq)Alternativa Alternativa ,()pqi)Alternativa Alternativa − − pqi,()pqj)Alternativa Alternativa − − pqj,()pqk)Alternativa Alternativa − − pqk].{f} {f} {f} {f} {f}f} {f} {f} {f} {f} {f}f} {f}f} {f} {f} {f} {f}f} {f}f} {f} {f}f}f}f}f} {f} {f}f}f}f} {f}f}f}f}f} {f}f}f} {f}f} {f}f}f}f}f}f}f}f}f} {f} {f}f}f} {f} {f}f}}f}f}f}f}f}f}f} {f}f}f}f}f}f}f}f}}}}f}
Puede encontrarse una derivación en.
Antecedentes
Cuaterniones
Los números complejos se pueden definir introduciendo un símbolo abstracto i que satisface las reglas usuales del álgebra y adicionalmente la regla i2 = −1. Esto es suficiente para reproducir todas las reglas de la aritmética de números complejos: por ejemplo:
- ()a+bi)()c+di)=ac+adi+bic+bidi=ac+adi+bci+bdi2=()ac− − bd)+()bc+ad)i.{displaystyle (a+bmathbf {i})(c+dmathbf {i})=ac+admathbf {i} +bmathbf {i} c+bmathbf {i} dmathbf {i} =ac+admathbf {i} +bcmathbf {i} +bdmathbf {i} ^{2}=(ac-bd)+(bc+ad)mathbf {i}.}
De la misma manera, los cuaterniones se pueden definir introduciendo símbolos abstractos i, j, k que cumplen las reglas i2 = j2 = k2 = i j k = −1 y las reglas algebraicas usuales excepto la ley conmutativa de la multiplicación (un ejemplo familiar de tal multiplicación no conmutativa es la multiplicación de matrices). De aquí se siguen todas las reglas de la aritmética de cuaterniones, como las reglas sobre la multiplicación de elementos básicos de cuaterniones. Usando estas reglas, se puede demostrar que:
- ()a+bi+cj+dk)()e+fi+gj+hk)=()ae− − bf− − cg− − dh)+()af+be+ch− − dg)i+()ag− − bh+ce+df)j+()ah+bg− − cf+de)k.{displaystyle {begin{aligned} ##dmathbf {k}(e+fmathbf {i} +gmathbf {j} +hmathbf {k})=\\(ae-bf-cg-dh)+(af+be+ch-dg)mathbf {i} +(ag-bh+ce+df)mathbf {j} +(ah+bg-cf+de)mathbf {k}end{aligned}}}}}}}}
La parte imaginaria bi+cj+dk{displaystyle bmathbf} +cmathbf {j} - ¿Qué? de una cuaternión se comporta como un vector v→ → =()b,c,d){displaystyle {vec {}=(b,c,d)} en el espacio vectorial tridimensional, y la parte real a se comporta como un escalar en R. Cuando se utilizan cuaternones en geometría, es más conveniente definirlos como un escalar más un vector:
- a+bi+cj+dk=a+v→ → .{displaystyle a+bmathbf {i} +cmathbf {j} +dmathbf {k} =a+{vec {v}}
Algunos pueden encontrar extraño agregar un número a un vector, ya que son objetos de naturalezas muy diferentes, o multiplicar dos vectores juntos, ya que esta operación suele ser indefinida. Sin embargo, si se recuerda que es una mera notación de las partes real e imaginaria de un cuaternión, se vuelve más legítimo. En otras palabras, el razonamiento correcto es la suma de dos cuaterniones, uno con cero vector/parte imaginaria, y otro con cero escalar/parte real:
- q1=s+v→ → =()s,0→ → )+()0,v→ → ).{displaystyle q_{1}=s+{vec {v}=left(s,{vec {0}right)+left(0,{vec {v}right). }
Podemos expresar la multiplicación de cuaterniones en el lenguaje moderno de los productos punto y cruz de vectores (que en realidad se inspiraron en los cuaterniones en primer lugar). Al multiplicar el vector/partes imaginarias, en lugar de las reglas i2 = j2 = k2 = ijk = −1 tenemos la regla de multiplicación de cuaterniones:
- v→ → w→ → =− − v→ → ⋅ ⋅ w→ → +v→ → × × w→ → ,{displaystyle {vec}{vec} {w}=-{vec} {}cdot {vec} {fnMicrosoft Sans Serif}
donde:
- v→ → w→ → {displaystyle {vec}{vec} {} es la cuaternión resultante,
- v→ → × × w→ → {displaystyle {vec}times {vec}} es producto de la cruz vectorial (un vector),
- v→ → ⋅ ⋅ w→ → {displaystyle {vec}cdot {vec}} es producto de escalar vectorial (un escalar).
La multiplicación de cuaterniones no es conmutativa (debido al producto vectorial, que es anticonmutador), mientras que las multiplicaciones escalar-escalar y escalar-vectorial conmutan. De estas reglas se sigue inmediatamente que (ver detalles):
- q1q2=()s+v→ → )()t+w→ → )=()st− − v→ → ⋅ ⋅ w→ → )+()sw→ → +tv→ → +v→ → × × w→ → ).{displaystyle q_{1}q_{2}=left(s+{vec {v}right)left(t+{vec {w}right)=left(st-{vec) {}cdot {vec}right)+left(s{vec] {w}+t{vec} {v}+{vec {}times {vec}right).}
El inverso multiplicativo o recíproco (izquierdo y derecho) de un cuaternión distinto de cero viene dado por la relación conjugada a norma (ver detalles):
- q1− − 1=()s+v→ → )− − 1=()s+v→ → )Alternativa Alternativa .. s+v→ → .. 2=s− − v→ → s2+.. v→ → .. 2,{displaystyle ¿Qué? Vert s+{vec {v}r Vert ^{2}={frac {S-{vec {} {fn} {fn}} {fn}} {fn}} {fn}}} {fn}}}} {fn}}}} {f}}}} {fn}}}} {fn}}}}} {f}}}}}}}} {c}}}}}}}}}}}} {c}}}}}}}}}}}}}}} {c}}}}}}}}}}}}}}}}}}}}}}} {c}}}}}}}}}}} {c}}}}}}}}}}}}}}}}} {c}} {c}}}}} {c}}} {c}}}}} {c}}}}}}}}}}}}}}}} {c}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} Vert {vec {}r Vert ^{2}}}}
como se puede verificar mediante cálculo directo (nótese la similitud con el inverso multiplicativo de los números complejos).
Identidad de rotación
Vamos u→ → {displaystyle {vec}} ser un vector de unidad (el eje de rotación) y dejar q=# α α 2+u→ → pecado α α 2{displaystyle q=cos {frac {fnMicrosoft} {fnMicroc} {fnMicroc} {fnMicrosoft} } {2}}. Nuestro objetivo es demostrar que
- v→ → .=qv→ → q− − 1=()# α α 2+u→ → pecado α α 2)v→ → ()# α α 2− − u→ → pecado α α 2){displaystyle {vec}=q{vec} {fnMicroc {fnMicrosoft} {fnMicroc {fnMicrosoft} {fnMicrosoft Sans Serif} {fnMicroc {fnMicroc}}derechoso),{vec {v}},left(cos {fracfracfnMicroc} {fnMicrosoft} - Sí.
cede el vector v→ → {displaystyle {vec}} girado por un ángulo α α {displaystyle alpha } alrededor del eje u→ → {displaystyle {vec}}. Ampliación (y teniendo en cuenta que u→ → v→ → =u→ → × × v→ → − − u→ → ⋅ ⋅ v→ → {displaystyle {vec}{vec} {}={vec {u}times {vec} {}-{vec {u}cdot {vec}}), tenemos
- v→ → .=v→ → #2 α α 2+()u→ → v→ → − − v→ → u→ → )pecado α α 2# α α 2− − u→ → v→ → u→ → pecado2 α α 2=v→ → #2 α α 2+2()u→ → × × v→ → )pecado α α 2# α α 2− − ()()u→ → × × v→ → )− − ()u→ → ⋅ ⋅ v→ → ))u→ → pecado2 α α 2=v→ → #2 α α 2+2()u→ → × × v→ → )pecado α α 2# α α 2− − ()()u→ → × × v→ → )u→ → − − ()u→ → ⋅ ⋅ v→ → )u→ → )pecado2 α α 2=v→ → #2 α α 2+2()u→ → × × v→ → )pecado α α 2# α α 2− − ()()()u→ → × × v→ → )× × u→ → − − ()u→ → × × v→ → )⋅ ⋅ u→ → )− − ()u→ → ⋅ ⋅ v→ → )u→ → )pecado2 α α 2=v→ → #2 α α 2+2()u→ → × × v→ → )pecado α α 2# α α 2− − ()()v→ → − − ()u→ → ⋅ ⋅ v→ → )u→ → )− − 0− − ()u→ → ⋅ ⋅ v→ → )u→ → )pecado2 α α 2=v→ → #2 α α 2+2()u→ → × × v→ → )pecado α α 2# α α 2− − ()v→ → − − 2u→ → ()u→ → ⋅ ⋅ v→ → ))pecado2 α α 2=v→ → #2 α α 2+2()u→ → × × v→ → )pecado α α 2# α α 2− − v→ → pecado2 α α 2+2u→ → ()u→ → ⋅ ⋅ v→ → )pecado2 α α 2=v→ → ()#2 α α 2− − pecado2 α α 2)+()u→ → × × v→ → )()2pecado α α 2# α α 2)+u→ → ()u→ → ⋅ ⋅ v→ → )()2pecado2 α α 2){displaystyle {begin{aligned}{vec} {fnK} {fnMicrosoft} {fnMicroc}} {fnK} {f} {fnK}} {f}}f}}}fn}}} {fnK}} {fn}}}}f}f}f}f}fnfnf}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}fnf}fnfnfnf}f}f}f}f}fnfnfnfnfnfnfnfnfnfnfnfnfnfnfn}fnfn}fnfn}fnf}fnfn}f}fn {fnMicrosoft} {fnK}+left({vec}{vec}{vec} {V}-{vec} {fnK} {fnMicroc {fnMicroc {fnMicrosoft Sans Serif} {fnK}cos {fnMicroc} {fnMicroc} {fnMicroc} {fnMicroc} {fnMicroc}}}} {fnMicroc}}}}}}fn}}}cos {fnMicroc {fnMicroc {fnMicroc}f}f}f}}}}}}}f}}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}c}f}f}f}f}c}f}f}f}fnf}f}f}cos {cos {cos {f}c}f}c}f }{2}-{vec {vec} {vec} {fnK} {fnK}fnh}fnh}\fnh00}[6pt] {fn} {fn}fn}fn} {fn}fn}fnK} {fn} {fnK}f}fn}fnK}f}fnKf}f}f}fnKfnKfn}f}f}fn}fnKfnKfnKfnKfnKfnKfnK}fnKfn}fnKfnKf}fn}f}fnKfnK}fnhnKfn}\fnhnKfnKfnKfnKfnKfnK}fnhnK}fnK}f}fnh}f}\fn {fnMicrosoft} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}fnMicrosoft Sans Serif} {fnK}cos {fnMicroc} {fnMicroc} {fnMicroc} {fnMicroc} {fnMicroc}}}} {fnMicroc}}}}}}fn}}}cos {fnMicroc {fnMicroc {fnMicroc}f}f}f}}}}}}}f}}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}c}f}f}f}f}c}f}f}f}fnf}f}f}cos {cos {cos {f}c}f}c}f {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {f}}cdot {v}right){vec} {c} {c} {c} {c} {c} {c} {c} {c} {c} {c} {c} {c}c} {c}c} {c}c} {c}c}c}c} {c}c}c}c}c}c}c}c}c}c}c}cc}c}cc}c}c}c}c}c}c}c}cccc}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c {fnMicrosoft} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}fnMicrosoft Sans Serif} {fnK}cos {fnMicroc} {fnMicroc} {fnMicroc} {fnMicroc} {fnMicroc}}}} {fnMicroc}}}}}}fn}}}cos {fnMicroc {fnMicroc {fnMicroc}f}f}f}}}}}}}f}}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}c}f}f}f}f}c}f}f}f}fnf}f}f}cos {cos {cos {f}c}f}c}f {fnMicrosoft Sans Serif} {fnMicrosoft} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}fnMicrosoft Sans Serif} {fnK}cos {fnMicroc} {fnMicroc} {fnMicroc} {fnMicroc} {fnMicroc}}}} {fnMicroc}}}}}}fn}}}cos {fnMicroc {fnMicroc {fnMicroc}f}f}f}}}}}}}f}}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}c}f}f}f}f}c}f}f}f}fnf}f}f}cos {cos {cos {f}c}f}c}f {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {f} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicros} {fnMicros} {fnMicrosoft} {fnMicrosoft}} {f} {f}f}f}}f}f}f}f}f}f}f} {f}f}f}f}f}f}fnMis}fnMis}f}f}f}f}fnKf}fnMis}fnMis}f}f}f}fnMis}fnMis}fnMis}fnMis}}fnMis}}fnMis}}fnMis}f}fnMi {fnMicrosoft} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}fnMicrosoft Sans Serif} {fnK}cos {fnMicroc} {fnMicroc} {fnMicroc} {fnMicroc} {fnMicroc}}}} {fnMicroc}}}}}}fn}}}cos {fnMicroc {fnMicroc {fnMicroc}f}f}f}}}}}}}f}}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}c}f}f}f}f}c}f}f}f}fnf}f}f}cos {cos {cos {f}c}f}c}f {} {fn} {fnK}} {fn}}} {fn}}} {fn}}cdot {c}c} {c}}}} {f} {fn} {fnK} {f}} {f}}} {f}}} {f}f}} {f} {f}f}}}f}}}}}f}}}}}}f}}}}f}f}}} {f}}}}}} {f} {f}f}}}}}f}f}f}}}f}f}}f}}f}f}}}}}}}}}}}}f}f}f}f}f}f}f}f}f}f}f}f} {f}f} {f}f}}}}}}}}} {fnMicrosoft} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}fnMicrosoft Sans Serif} {fnK}cos {fnMicroc} {fnMicroc} {fnMicroc} {fnMicroc} {fnMicroc}}}} {fnMicroc}}}}}}fn}}}cos {fnMicroc {fnMicroc {fnMicroc}f}f}f}}}}}}}f}}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}c}f}f}f}f}c}f}f}f}fnf}f}f}cos {cos {cos {f}c}f}c}f }{2}-left({vec {}-2{vec {u}left({vec {u}cdot {vec {vec}right)derecha)sin ^{2}{2}[6pt] {fnMicrosoft} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}fnMicrosoft Sans Serif} {fnK}cos {fnMicroc} {fnMicroc} {fnMicroc} {fnMicroc} {fnMicroc}}}} {fnMicroc}}}}}}fn}}}cos {fnMicroc {fnMicroc {fnMicroc}f}f}f}}}}}}}f}}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}c}f}f}f}f}c}f}f}f}fnf}f}f}cos {cos {cos {f}c}f}c}f # {2}-{vec}sin {fnMicrosoft} {fnK}cdot {fnh}cdot {fnh}cdot {v}right)sin ^{2}{frac {alpha }\[6pt] âTMa}cdot {cdot {fnc {c}ccH00}c}ccH00}cH00}cdot}cH0}cdot}c}cdot}c}cdot}cdot}c}cdot}cccccdot}c}c}c}c}cdot {c}cdot {c}cdot}c}cdot}\ccdot\cdot {c}cdot {cdot {c}cdot {c}c}cdot}c}cdot} {fnMicrosoft} ## {2}-sin ^{2}{frac {alpha {fnMicrosoft Sans Serif}fnMicros {fnMicrosoft Sans Serif}left(2sin {frac} {fnMicrosoft} {fnK}cos {fnMicroc} {fnMicroc} {fnMicroc} {fnMicroc} {fnMicroc}}}} {fnMicroc}}}}}}fn}}}cos {fnMicroc {fnMicroc {fnMicroc}f}f}f}}}}}}}f}}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}c}f}f}f}f}c}f}f}f}fnf}f}f}cos {cos {cos {f}c}f}c}f {fnK}cdot {c}cdot {c}cdot {c}i}i}left(2sin ^{2}{frac {alpha }{2}derecho)[6pt]end{aligned}}}}}} {}}}} {c}} {c}}}}}}} {c}}}}}}}}}}}}}c}}}}}}c}}c}}}}}}}}}c]c]c}c]c}}c]c}}c}c}c}}c}c]c]c]c}c]c]c]c]ccc}c]cdotc}}cdotpcdotc}c]c}cdotcdotcdotcdot
Usando identidades trigonométricas:
- v→ → .=v→ → ()#2 α α 2− − pecado2 α α 2)+()u→ → × × v→ → )()2pecado α α 2# α α 2)+u→ → ()u→ → ⋅ ⋅ v→ → )()2pecado2 α α 2)=v→ → # α α +()u→ → × × v→ → )pecado α α +u→ → ()u→ → ⋅ ⋅ v→ → )()1− − # α α )=v→ → # α α +()u→ → × × v→ → )pecado α α +u→ → ()u→ → ⋅ ⋅ v→ → )− − u→ → ()u→ → ⋅ ⋅ v→ → )# α α =()v→ → − − u→ → ()u→ → ⋅ ⋅ v→ → ))# α α +()u→ → × × v→ → )pecado α α +u→ → ()u→ → ⋅ ⋅ v→ → )=v→ → ⊥ ⊥ # α α +()u→ → × × v→ → )pecado α α +v→ → .. {displaystyle {begin{aligned}{vec} {fnK} {f}fnK} {f}fnK} {f}} {f}f}fn} {f}fn}fn}fnK} {f} {fnK}}} {f}fnf}f}fnfnK}f}f}f}f}f}f}f}f}f}f}f}f}c}f}f}c}fnf}c}f}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c} {fnMicrosoft} ## {2}-sin ^{2}{frac {alpha {fnMicrosoft Sans Serif}fnMicros {fnMicrosoft Sans Serif}left(2sin {frac} {fnMicrosoft} {fnK}cos {fnMicroc} {fnMicroc} {fnMicroc} {fnMicroc} {fnMicroc}}}} {fnMicroc}}}}}}fn}}}cos {fnMicroc {fnMicroc {fnMicroc}f}f}f}}}}}}}f}}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}c}f}f}f}f}c}f}f}f}fnf}f}f}cos {cos {cos {f}c}f}c}f {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {f}}}} {c} {c}c} {c}c} {c}c}c} {c}c} {c}c}c}cc}c}cc}c}c}c}c}c}c}c}c}c}c}c}c}c}c}cc}c}c}c}c}c}c}c}c}c}c}cc}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c} ##{vec {u}left({vec {u}cdot {vec {vec}right)left(1-cos alpha right)[6pt] limit={vec {v}cos alpha +left({vec {u}times {vecvec}derech] {fnMicrosoft Sans Serif} ###{vec {u}cdot {vec {vec}right)\[6pt] limit={vec {v}_{bot }cos alpha +left({vec {u}times {vec {vec}right)sin alpha +{vec {fnh} {fnK}fnK}} {fnK}} {fn}fn}fn}fn}fn}fn}fnK}} {fnK}}fnfn}fnfn}f}fnfnKfnK}fn}\\\\fnfn}fn}fn}fn}fn}fnfn}fn}fn}fn}\fn}\fn}fn}fn}fn}\\fn}fnfn}fn}fn}fn}fn}fnfnfnfn}fn}fn}fn}fn}fn}fn\fn}fn}fn}\fn}fn
Donde v→ → ⊥ ⊥ {displaystyle {vec}_{bots} y v→ → .. {displaystyle {vec}_{fncip}} son los componentes v→ (perpendicular y paralelo a u→ respectivamente). Esta es la fórmula de una rotación por α α {displaystyle alpha } alrededor de la u→ Axis.
Operaciones de rotación de cuaterniones
Altman proporciona una explicación muy formal de las propiedades utilizadas en esta sección.
La hiperesfera de rotaciones
Visualizando el espacio de rotaciones
Los cuaterniones unitarios representan el grupo de rotaciones euclidianas en tres dimensiones de una manera muy sencilla. La correspondencia entre rotaciones y cuaterniones se puede entender visualizando primero el propio espacio de rotaciones.
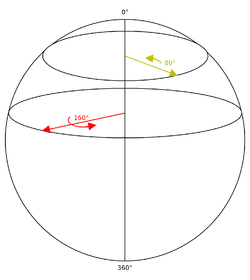
Para visualizar el espacio de rotaciones, ayuda considerar un caso más simple. Cualquier rotación en tres dimensiones puede describirse mediante una rotación de algún ángulo alrededor de algún eje; para nuestros propósitos, usaremos un eje vector para establecer la lateralidad de nuestro ángulo. Considere el caso especial en el que el eje de rotación se encuentra en el plano xy. Entonces podemos especificar el eje de una de estas rotaciones por un punto en un círculo a través del cual cruza el vector, y podemos seleccionar el radio del círculo para indicar el ángulo de rotación.
Del mismo modo, una rotación cuyo eje de rotación se encuentra en el plano xy puede describirse como un punto en una esfera de radio fijo en tres dimensiones. Comenzando en el polo norte de una esfera en el espacio tridimensional, especificamos que el punto en el polo norte es la rotación de identidad (una rotación de ángulo cero). Al igual que en el caso de la rotación de identidad, no se define ningún eje de rotación y el ángulo de rotación (cero) es irrelevante. Una rotación que tiene un ángulo de rotación muy pequeño se puede especificar mediante un corte a través de la esfera paralelo al plano xy y muy cerca del polo norte. El círculo definido por este corte será muy pequeño, correspondiente al pequeño ángulo de rotación. A medida que los ángulos de rotación aumentan, el corte se mueve en la dirección negativa z y los círculos aumentan hasta alcanzar el ecuador de la esfera, lo que corresponderá a un ángulo de rotación de 180 grados. Continuando hacia el sur, los radios de los círculos ahora se vuelven más pequeños (correspondientes al valor absoluto del ángulo de rotación considerado como un número negativo). Finalmente, cuando se alcanza el polo sur, los círculos se encogen una vez más hasta la rotación de identidad, que también se especifica como el punto en el polo sur.
Observe que esta visualización puede ver varias características de tales rotaciones y sus representaciones. El espacio de rotaciones es continuo, cada rotación tiene una vecindad de rotaciones que son casi iguales, y esta vecindad se vuelve plana a medida que la vecindad se encoge. Además, cada rotación en realidad está representada por dos puntos antípodas en la esfera, que están en los extremos opuestos de una línea que pasa por el centro de la esfera. Esto refleja el hecho de que cada rotación puede representarse como una rotación alrededor de algún eje o, de manera equivalente, como una rotación negativa alrededor de un eje que apunta en la dirección opuesta (la llamada doble cubierta). La "latitud" de un círculo que representa un ángulo de rotación particular será la mitad del ángulo representado por esa rotación, ya que a medida que el punto se mueve del polo norte al polo sur, la latitud varía de cero a 180 grados, mientras que el ángulo de rotación varía de 0 a 360 grados. (la "longitud" de un punto representa un eje de rotación particular). Sin embargo, tenga en cuenta que este conjunto de rotaciones no está cerrado en la composición. Dos rotaciones sucesivas con ejes en el plano xy no necesariamente darán una rotación cuyo eje se encuentre en el plano xy y, por lo tanto, no se puede representar como un punto en la esfera. Este no será el caso con una rotación general en 3 espacios, en la que las rotaciones forman un conjunto cerrado bajo composición.
Esta visualización se puede extender a una rotación general en un espacio tridimensional. La rotación de identidad es un punto, y un pequeño ángulo de rotación alrededor de algún eje se puede representar como un punto en una esfera con un radio pequeño. A medida que crece el ángulo de rotación, la esfera crece, hasta que el ángulo de rotación alcanza los 180 grados, momento en el que la esfera comienza a encogerse y se convierte en un punto cuando el ángulo se acerca a los 360 grados (o cero grados desde la dirección negativa). Este conjunto de esferas que se expanden y contraen representa una hiperesfera en un espacio de cuatro dimensiones (una esfera tridimensional). Al igual que en el ejemplo anterior más simple, cada rotación representada como un punto en la hiperesfera se corresponde con su punto antípoda en esa hiperesfera. La "latitud" en la hiperesfera será la mitad del ángulo de rotación correspondiente, y la vecindad de cualquier punto se volverá "más plana" (es decir, ser representado por un espacio euclidiano tridimensional de puntos) a medida que la vecindad se reduce. Este comportamiento se corresponde con el conjunto de cuaterniones unitarios: un cuaternión general representa un punto en un espacio de cuatro dimensiones, pero restringirlo para que tenga una magnitud unitaria produce un espacio tridimensional equivalente a la superficie de una hiperesfera. La magnitud del cuaternión unidad será la unidad, correspondiente a una hiperesfera de radio unidad. La parte vectorial de un cuaternión unitario representa el radio de la 2-esfera correspondiente al eje de rotación, y su magnitud es el coseno de la mitad del ángulo de rotación. Cada rotación está representada por dos cuaterniones unitarios de signo opuesto y, como en el espacio de rotaciones en tres dimensiones, el producto de cuaterniones de dos cuaterniones unitarios producirá un cuaternión unitario. Además, el espacio de los cuaterniones unitarios es "plano" en cualquier vecindad infinitesimal de un cuaternión unitario dado.
Parametrización del espacio de rotaciones
Podemos parametrizar la superficie de una esfera con dos coordenadas, como la latitud y la longitud. Pero la latitud y la longitud se comportan mal (degeneran) en los polos norte y sur, aunque los polos no son intrínsecamente diferentes de cualquier otro punto de la esfera. En los polos (latitudes +90° y −90°), la longitud deja de tener sentido.
Se puede demostrar que ningún sistema de coordenadas de dos parámetros puede evitar tal degeneración. Podemos evitar tales problemas incrustando la esfera en el espacio tridimensional y parametrándola con tres coordenadas cartesianas ()w,x,Sí.), colocando el polo norte en ()w,x,Sí.) = (1, 0, 0), el polo sur en ()w,x,Sí.) = (−1, 0, 0), y el Ecuador w = 0, x2 + Sí.2 = 1. Los puntos en la esfera satisfacen la limitación w2 + x2 + Sí.2 = 1Así que todavía tenemos sólo dos grados de libertad aunque hay tres coordenadas. Un punto ()w,x,Sí.) en la esfera representa una rotación en el espacio ordinario alrededor del eje horizontal dirigido por el vector ()x,Sí., 0) por un ángulo α α =2#− − 1 w=2pecado− − 1 x2+Sí.2{displaystyle alpha =2cos ^{-1}w=2sin ^{-1}{sqrt {x^{2}+y^{2}}}.
De la misma manera, el espacio hiperesférico de las rotaciones 3D puede ser parametizado por tres ángulos (ángulos Euler), pero cualquier parametrización de este tipo es degenerada en algunos puntos en la hipersfera, lo que conduce al problema del bloqueo gimbal. Podemos evitarlo usando cuatro coordenadas de Euclidean w,x,Sí.,z, con w2 + x2 + Sí.2 + z2 = 1. El punto ()w,x,Sí.,z) representa una rotación alrededor del eje dirigido por el vector ()x,Sí.,z) por un ángulo α α =2#− − 1 w=2pecado− − 1 x2+Sí.2+z2.{displaystyle alpha =2cos ^{-1}w=2sin ^{-1}{sqrt {x^{2}+y^{2}+z^{2}}}
Explicando los cuaterniones' propiedades con rotaciones
No conmutatividad
La multiplicación de cuaterniones no es conmutativa. Este hecho explica cómo la fórmula p ↦ q p q−1 puede funcionar, teniendo q q−1 = 1 por definición. Dado que la multiplicación de cuaterniones unitarios corresponde a la composición de rotaciones tridimensionales, esta propiedad se puede hacer intuitiva mostrando que las rotaciones tridimensionales no son conmutativas en general.
Coloca dos libros uno al lado del otro. Gira uno de ellos 90 grados en el sentido de las agujas del reloj alrededor del eje z y luego gíralo 180 grados alrededor del eje x. Toma el otro libro, gíralo 180° alrededor del eje x primero, y 90° en el sentido de las agujas del reloj alrededor de z después. Los dos libros no terminan paralelos. Esto muestra que, en general, la composición de dos rotaciones diferentes alrededor de dos ejes espaciales distintos no conmutará.
Orientación
El producto de la cruz vectorial, utilizado para definir la representación del eje-ángulo, confiere una orientación ("manedness") al espacio: en un espacio vectorial tridimensional, los tres vectores en la ecuación a×b = c formará siempre un conjunto con las manos derechas (o un conjunto con las manos izquierdas, dependiendo de cómo se defina el producto cruzado), fijando así una orientación en el espacio vectorial. Alternativamente, la dependencia de la orientación se expresa al referirse a ello u→ → {displaystyle {vec}} que especifica una rotación vectores axiales. En el formalismo cuaternónico la elección de una orientación del espacio corresponde al orden de multiplicación: ij = k pero ji =k. Si uno revierte la orientación, entonces la fórmula anterior se convierte p ↦ q−1p q, es decir, una unidad q es reemplazado por la cuaternión conjugada – el mismo comportamiento que los vectores axiales.
Convenciones alternativas
It is reported that the existence and continued use of an alternative quaternion convention in the aerospace and, to a lesser extent, robics community is incurring a costo significativo y continuo [sic]. Esta convención alternativa es propuesta por Shuster M.D. en y se aleja de la tradición revirtiendo la definición para multiplicar elementos de base de quaternion tales que bajo la convención de Shuster, ij=− − k{displaystyle mathbf {i} mathbf {j} =-mathbf {k} mientras que la definición de Hamilton es ij=k{displaystyle mathbf {i} mathbf {j} =mathbf {k}. Esta convención también se denomina "Convención JPL" para su uso en algunas partes del Laboratorio de Propulsión Jet de la NASA.
Bajo la convención de Shuster, la fórmula para multiplicar dos cuaterniones se altera de tal manera que
- ()r1,v→ → 1)()r2,v→ → 2)=()r1r2− − v→ → 1⋅ ⋅ v→ → 2,r1v→ → 2+r2v→ → 1− − v→ → 1× × v→ → 2),(Convención alternativa, uso desalentado!){displaystyle left(r_{1}, {vec {v}_{1}right)left(r_{2}, {vec {v}_{2}right)=left(r_{1}r_{2}-{vec} {}_{1}cdot {vec}_{2}, r_{1}{vec} {vec} {fnMicrosoft} {fnMicrosoft} {fnMicrosoft} {fn}}} {fn}}}} {fn}} {fn}} {fn}}}}fnfn}}}\\fn}}}\\fn}}}\fn}}}}}\\\\fn}}}}}}}\\\\\\\c}}}}}}}}}}\\\\\\c}}}}}}}}}}}\\\\\\\\\\\\\c}}}}}}}}}}}\\\\\\\\c}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {}_{1}mathbin {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}}}} {fnMicrosoft Sans Serif}
La fórmula para rotar un vector por un cuaternión se modifica para ser
- pAlt.=()v⊗ ⊗ v+qr2I− − 2qr[v]× × +[v]× × 2)p(Convención alternativa, uso desalentado!)=()I− − 2qr[v]× × +2[v]× × 2)p{displaystyle {begin{aligned}mathbf {p} {text{alt}={} {mathbf {v}otimes mathbf {v} #### ############################################################################################################################################################################################################################################################ {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}
Para identificar los cambios según la convención de Shuster, observe que el signo anterior al producto vectorial se invierte de más a menos.
Finalmente, la fórmula para convertir un cuaternión en una matriz de rotación se modifica para ser
- Ralt=I− − 2qr[v]× × +2[v]× × 2(Convención alternativa, uso desalentado!)=[1− − 2s()qj2+qk2)2()qiqj+qkqr)2()qiqk− − qjqr)2()qiqj− − qkqr)1− − 2s()qi2+qk2)2()qjqk+qiqr)2()qiqk+qjqr)2()qjqk− − qiqr)1− − 2s()qi2+qj2)]{displaystyle {begin{aligned}mathbf {R} _{alt} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}
que es exactamente la transpuesta de la matriz de rotación convertida según la convención tradicional.
Aplicaciones de software por convención utilizadas
La siguiente tabla agrupa las aplicaciones según su adhesión a cualquiera de las convenciones de cuaterniones:
| Convención de multiplicación de Hamilton | Convención de multiplicación de Shuster |
|---|---|
|
|
Si bien el uso de cualquiera de las convenciones no afecta la capacidad o la corrección de las aplicaciones así creadas, los autores argumentaron que la convención de Shuster debe abandonarse porque se aparta de la convención de multiplicación de cuaterniones mucho más antigua de Hamilton y es posible que nunca sea adoptada por el áreas de la física matemática o teórica.
Comparación con otras representaciones de rotaciones
Ventajas de los cuaterniones
La representación de una rotación como cuaternión (4 números) es más compacta que la representación como matriz ortogonal (9 números). Además, para un eje y ángulo dados, se puede construir fácilmente el cuaternión correspondiente y, a la inversa, para un cuaternión dado, se puede leer fácilmente el eje y el ángulo. Ambos son mucho más difíciles con matrices o ángulos de Euler.
En los videojuegos y otras aplicaciones, uno suele estar interesado en las "rotaciones suaves", lo que significa que la escena debe rotar lentamente y no en un solo paso. Esto se puede lograr eligiendo una curva como la interpolación lineal esférica en los cuaterniones, siendo un punto final la transformación de identidad 1 (o alguna otra rotación inicial) y el otro la rotación final prevista. Esto es más problemático con otras representaciones de rotaciones.
Al componer varias rotaciones en una computadora, los errores de redondeo necesariamente se acumulan. Un cuaternión que está ligeramente desviado aún representa una rotación después de ser normalizado: una matriz que está ligeramente desviada puede que ya no sea ortogonal y es más difícil volver a convertirla en una matriz ortogonal propiamente dicha.
Los cuaterniones también evitan un fenómeno llamado bloqueo de cardán que puede producirse cuando, por ejemplo, en los sistemas rotativos de cabeceo/guiñada/balanceo, el cabeceo gira 90° hacia arriba o hacia abajo, de modo que la guiñada y el balanceo corresponden al mismo movimiento, y se pierde un grado de libertad de rotación. En un sistema de navegación inercial aeroespacial basado en cardán, por ejemplo, esto podría tener resultados desastrosos si la aeronave se encuentra en un descenso o ascenso pronunciado.
Conversión hacia y desde la representación matricial
De un cuaternión a una matriz ortogonal
La matriz ortogonal correspondiente a una rotación por la unidad cuaternión z = a + b i + c j + d k (con | z | = 1) cuando la posmultiplicación con un vector columna viene dada por
- R=()a2+b2− − c2− − d22bc− − 2ad2bd+2ac2bc+2ada2− − b2+c2− − d22cd− − 2ab2bd− − 2ac2cd+2aba2− − b2− − c2+d2).{displaystyle {2}-c^{2}-b^{2}-d^{2}-d^{2}-d^{2}-d^{2}-d^{2}2d+2ac2bc+2ad
Esta matriz de rotación se utiliza en vectores w como wrotativa=R⋅ ⋅ w{displaystyle ¿Qué?. La representación de esta rotación es dada por:
- [0wrotativa]=z[0w]zAlternativa Alternativa ,{displaystyle {begin{bmatrix}0\w_{text{rotated}end{bmatrix}}=z{begin{bmatrix}0wend{bmatrix}}z^{*}}}}}}
Donde zAlternativa Alternativa {displaystyle z^{*} es el conjugado de la cuaternión z{displaystyle z}, dado por zAlternativa Alternativa =a− − bi− − cj− − dk{displaystyle mathbf {z} ^{*}=a-bmathbf {i} -cmathbf {j} -D 'mathbf {k}
Además, la multiplicación de cuaterniones se define como (asumiendo que a y b son cuaterniones, como z arriba):
ab=()a0b0− − a→ → ⋅ ⋅ b→ → ;a0b→ → +b0a→ → +a→ → × × b→ → ){displaystyle ab=left (a_{0}b_{0}-{vec {cdot {vec} {b};a_{0}{vec} {b}+b_{0}{vec} {a}+{vec {}times {vec}right)}
donde el orden a, b es importante ya que el producto vectorial de dos vectores no es conmutativo.
Un cálculo más eficiente en el que el cuaternión no necesita normalizarse por unidad viene dado por
- R=()1− − cc− − ddbc− − adbd+acbc+ad1− − bb− − ddcd− − abbd− − accd+ab1− − bb− − cc),{displaystyle R={begin{pmatrix}1-cc-dd implicabc-ad limitbd+acbc+ad limit1-bb-dd implicacd-ab\bd-ac limitcd+ab limit1-bb-cc\\\end{pmatrix}}}
donde se han definido las siguientes cantidades intermedias:
- s=2/()a⋅ ⋅ a+b⋅ ⋅ b+c⋅ ⋅ c+d⋅ ⋅ d),bs=b⋅ ⋅ s,cs=c⋅ ⋅ s,ds=d⋅ ⋅ s,ab=a⋅ ⋅ bs,ac=a⋅ ⋅ cs,ad=a⋅ ⋅ ds,bb=b⋅ ⋅ bs,bc=b⋅ ⋅ cs,bd=b⋅ ⋅ ds,cc=c⋅ ⋅ cs,cd=c⋅ ⋅ ds,dd=d⋅ ⋅ ds.{fnMicrosoft Sans Serif}
De matriz ortogonal a cuaternión
Se debe tener cuidado al convertir una matriz de rotación en un cuaternión, ya que varios métodos sencillos tienden a ser inestables cuando la traza (suma de los elementos diagonales) de la matriz de rotación es cero o muy pequeña. Para conocer un método estable de convertir una matriz ortogonal en un cuaternión, consulte Rotation matrix#Quaternion.
Ajuste de cuaterniones
La sección anterior describe cómo recuperar un cuaternión q de una matriz de rotación de 3 × 3 Q. Sin embargo, supongamos que tenemos una matriz Q que no es una rotación pura, debido a errores de redondeo, por ejemplo. y deseamos encontrar el cuaternión q que representa con mayor precisión P. En ese caso construimos una matriz simétrica de 4 × 4
- K=13[Qxx− − QSí.Sí.− − QzzQSí.x+QxSí.Qzx+QxzQzSí.− − QSí.zQSí.x+QxSí.QSí.Sí.− − Qxx− − QzzQzSí.+QSí.zQxz− − QzxQzx+QxzQzSí.+QSí.zQzz− − Qxx− − QSí.Sí.QSí.x− − QxSí.QzSí.− − QSí.zQxz− − QzxQSí.x− − QxSí.Qxx+QSí.Sí.+Qzz],{displaystyle K={frac {x} {x}
y encuentre el vector propio (x, y, z, w) correspondiente al mayor valor propio (ese valor será 1 si y solo si Q es una rotación pura). El cuaternión así obtenido corresponderá a la rotación más cercana a la matriz original Q.
Comparaciones de rendimiento
Esta sección analiza las implicaciones de rendimiento del uso de cuaterniones frente a otros métodos (matrices de eje/ángulo o rotación) para realizar rotaciones en 3D.
Resultados
| Método | Almacenamiento |
|---|---|
| Matriz de rotación | 9 |
| Quaternion | 3 o 4 (véase infra) |
| Ángulo: eje | 3 o 4 (véase infra) |
Solo tres de los componentes del cuaternión son independientes, ya que una rotación está representada por una unidad de cuaternión. Para un cálculo posterior, generalmente se necesitan los cuatro elementos, por lo que todos los cálculos sufrirían un gasto adicional al recuperar el cuarto componente. Del mismo modo, el eje-ángulo se puede almacenar en un vector de tres componentes multiplicando la dirección de la unidad por el ángulo (o una función del mismo), pero esto tiene un costo computacional adicional cuando se usa para los cálculos.
| Método | # multiplicas | # add/subtracts | Total de operaciones |
|---|---|---|---|
| Matrices de rotación | 27 | 18 | 45 |
| Quaternions | 16 | 12 | 28 |
| Método | # multiplicas | # add/subtracts | # pecado/cos | Total de operaciones | |
|---|---|---|---|---|---|
| Matriz de rotación | 9 | 6 | 0 | 15 | |
| Quaternions * | Sin matriz intermedia | 15 | 15 | 0 | 30 |
| Con matriz intermedia | 21 | 18 | 0 | 39 | |
| Ángulo: eje | Sin matriz intermedia | 18 | 13 | 2 | 30 + 3 |
| Con matriz intermedia | 21 | 16 | 2 | 37 + 2 | |
* Los cuaterniones se pueden convertir implícitamente en una matriz similar a una rotación (12 multiplicaciones y 12 sumas/restas), que nivela los siguientes costos de rotación de vectores con el método de matriz de rotación.
Métodos utilizados
Hay tres enfoques básicos para rotar un vector v →:
- Computar el producto de matriz de una matriz de rotación 3 × 3 R y la matriz original de columna 3 × 1 v→. Esto requiere 3 × (3 multiplicaciones + 2 adiciones) = 9 multiplicaciones y 6 adiciones, el método más eficiente para rotar un vector.
- Una rotación puede ser representada por una cuaternión de longitud unitaria q =w,r→) con escalar (real) parte w y parte vectorial (imaginaria) r→. La rotación se puede aplicar a un vector 3D v→ a través de la fórmula v→ → nuevo=v→ → +2r→ → × × ()r→ → × × v→ → +wv→ → ){displaystyle {vec {fnK} {fnMicrosoft}= {fnMicrosoft} {}+2{vec {r}times ({vec {r}times {vec {vec}+w{vec {v}}}})}. Esto requiere sólo 15 multiplicaciones y 15 adiciones para evaluar (o 18 multiplicaciones y 12 adiciones si el factor de 2 se hace a través de la multiplicación). Esta fórmula, originalmente pensada para ser utilizada con axis/ángulo notación (fórmula de Rodrigues), también se puede aplicar a la notación de cuaternión. Esto produce el mismo resultado que la fórmula menos eficiente pero más compacta de multiplicación de cuaternión v→ → nuevo=qv→ → q− − 1{displaystyle {vec {fnMicrosoft}=q{vec} {fnK}.
- Utilice la fórmula de ángulo/eje para convertir un ángulo/eje a una matriz de rotación R entonces multiplicarse con un vector, o, de forma similar, utilizar una fórmula para convertir notación de cuaternión a una matriz de rotación, luego multiplicarse con un vector. Convertir el ángulo/eje en R cuesta 12 multiplicaciones, 2 llamadas de función (sin, cos), y 10 adiciones/subtracciones; desde el punto 1, girando utilizando R añade 9 multiplicaciones y 6 adiciones adicionales para un total de 21 multiplicaciones, 16 adiciones/subtracciones y 2 llamadas de función (sin, porque). Convertir una cuaternión en R cuesta 12 multiplicaciones y 12 adiciones/subtracciones; desde el punto 1, girando utilizando R añade 9 multiplicaciones y 6 adiciones adicionales para un total de 21 multiplicaciones y 18 adiciones/subtracciones.
| Método | # multiplicas | # add/subtracts | # pecado/cos | Total de operaciones | |
|---|---|---|---|---|---|
| Matriz de rotación | 9n | 6n | 0 | 15n | |
| Quaternions * | Sin matriz intermedia | 15n | 15n | 0 | 30n |
| Con matriz intermedia | 9n + 12 | 6n + 12 | 0 | 15n + 24 | |
| Ángulo: eje | Sin matriz intermedia | 18n | 12n + 1 | 2 | 30n + 3 |
| Con matriz intermedia | 9n + 12 | 6n + 10 | 2 | 15n + 24 | |
Pares de cuaterniones unitarios como rotaciones en el espacio 4D
Un par de cuaterniones unitarios zl y zr puede representar cualquier rotación en el espacio 4D. Dado un vector de cuatro dimensiones v→, y asumiendo que es un cuaternión, podemos rotar el vector v→ así:
- f()v→ → )=zlv→ → zr=()al− − bl− − cl− − dlblal− − dlclcldlal− − bldl− − clblal)()wxSí.z)()ar− − br− − cr− − drbrardr− − crcr− − drarbrdrcr− − brar).{displaystyle fleft({vec}right)=mathbf {z} ¿Qué? Mathbf {z} {}={begin {pmatrix}a_{rm} {I}} {fn} {fn} {fn}}} {fnfn} {fn} {fn}}} {fn}}} {c}}}} {c}}}} {c}}} {c}}}} {c_}}}}}}}}}}}}}}}}}}} {c_}}}}}}}}}}}}}} {m}}}}}}}}}}}}} {m}}}}} {m} {m} {m}}}}}} {m}}}}}}}}}}}}}}}}}} {m}}}}}} {m} {m} {m}} {m}}} {c_}}}}}}}}}}}}} {c_}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {c} {c} {c}} {c} {c} {c} {c} {c}} {rm} {c} {c} {c}} {c}} {c} {c}}}} {m}} {m} {m}}}} {m}}} {m}}}} {m} {m}}}}} {m}} {m} {m}} {m}} {m}} {m}}}}} {m}} {m}}} {m}}}}}}}}}}}}}} {m}}}}} {m} {m} {m} {m} {m} {m}} {m} {m}}}}}}}}}}}}}} {m}}}}}}}}}}}}}}}}} {m}}}}}}}}}} {c} {c} {c} {c}} {cc}} {ccccccccH}}} {begin{pmatrix}w\x\y\cccccccccccccccccccccccccccccccccccccccccccccccccccccccccc}}}}}}}}}}}}}} {ccccccccccccc}}}}}}}}}}}} {cccccccccH {fn} {fnMicrosoft} {fnMicrosoft}} {fnMicrosoft}}} {cH}}}} {fn}}}}}} {fn} {fn}}} {fnfn}}} {cHFF} {cHFF} {cHFF} {cHFF} {cH00}} {cH00}}} {fn}b} {fnh} {fnh} {fnh} {fnh} {fn} {f}}} {fn} {fn}}}} {fn}}}}b} {b} {b} {b} {c}}}} {c}}}}}}}}}}b}b}}}} {b}}}} {b}}}}}}}}}}}} {b} {b}}}} {b}}}} {b} {c\c} {c}}}}}}}}}}}}}} {b} {c}}}} {c}}}} {c}}}}} {ccccc}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {cHFF} {cHFF} {r}c_{rm} {fn} {fn} {fn}} {fn}} {fn}} {fn} {fn}}} {fn}}}}}} {cH}}}}}} {cH}}}}}} {c}} {c}}}}}} {c}}}}}}}}}}}}}}}}}}}}}} {c}}}}}} {c}}}} {rm}}}} {c}}}}}}}}}}} {c}}}}}}}}}}} {c}}}}}}}}}}}}}}}}}}} {c}}}}}}}}}}}}}} {cccccc}}}}}}}}}} {c}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {r}d_{rm} {fnh}} {R}} {fn} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}
El par de matrices representa una rotación de R4. Tenga en cuenta que desde entonces ()zlv→ → )zr=zl()v→ → zr){displaystyle (mathbf {z} {fn} {fnh} {fnh})mathbf {z} ¿Qué?Las dos matrices deben comunicarse. Por lo tanto, hay dos subgrupos de conmutación del grupo de rotaciones dimensionales. Las rotaciones cuatridimensionales arbitrarias tienen 6 grados de libertad; cada matriz representa 3 de esos 6 grados de libertad.
Dado que los generadores de las rotaciones de cuatro dimensiones se pueden representar mediante pares de cuaterniones (como se muestra a continuación), todas las rotaciones de cuatro dimensiones también se pueden representar.
- zlv→ → zr=()1− − dtab− − dtac− − dtaddtab1− − dtbc− − dtbddtacdtbc1− − dtcddtaddtbddtcd1)()wxSí.z)zl=1+dtab+dtcd2i+dtac− − dtbd2j+dtad+dtbc2kzr=1+dtab− − dtcd2i+dtac+dtbd2j+dtad− − dtbc2k{c} {c} {c} {c}c} {c}}} {c}} {c} {c}} {c}}} {c} {c}} {c}c}} {c} {c} {c}c} {c}c}c}} {c} {c}}}}} {c}}}}}} {c}}}}}} {cc}}}}}}}} {c} {c}c}}ccc} {cc}}cc}}}}}}}ccc}}}}ccccc}cccccc}ccccccc}cccc}ccc}cccc}ccc}}}cc} over 2}i+{dt_{ac}-dt_{bd} over 2}j+{dt_{ad}+dt_{bc} over 2}k[3pt]mathbf {z} _{rm {fn} {cHFF}}}}=1+{dt_{ab}-dt_{cd} over 2}i+{dt_{ac}+dt_{bd} over 2}j+{dt_{ad}-dt_{bc} {fnMicrosoft}
Enlaces y recursos externos
- Shoemake, Ken. (PDF). Archivado (PDF) del original el 2020-05-03.
- "Simple Quaternion tipo y operaciones en más de setenta y cinco idiomas informáticos". on Rosetta Code
- Hart, John C. "Quaternion Demonstrator".
- Dam, Eik B.; Koch, Martin; Lillholm, Martin (1998). "Quaternions, Interpolation and Animation" (PDF).
- Leandra, Vicci (2001). "Cuaternions and Rotations in 3-Space: The Algebra and its Geometric Interpretation" (PDF).
- Howell, Thomas; Lafon, Jean-Claude (1975). "The Complexity of the Quaternion Product, TR75-245" (PDF). Universidad Cornell.
- Horn, Berthold K.P. (2001). "Some Notes on Unit Quaternions and Rotation" (PDF).
- Lee, Byung-Uk (1991). Unidad Quaternion Representation of Rotation - Apéndice A, Diferenciación con Quaternions - Apéndice B (PDF) (Ph. D. Thesis). Universidad de Stanford.
- Vance, Rod. "Algunos ejemplos de grupos de mentira conectados". Archivado desde el original en 2018-12-15.
- " Representación visual de la rotación de la cuaternión".
Contenido relacionado
Curtosis
Transmisiones (telecomunicaciones)
Ataque con drones





![[0,2pi]](https://wikimedia.org/api/rest_v1/media/math/render/svg/348d40bf3f8b7e1c00c4346440d7e2e4f0cc9b91)







































![{displaystyle {begin{aligned}(0, mathbf {p} ')=&((q_{r}, mathbf {v})(0, mathbf {p}))s(q_{r}, -mathbf {v})\=&(q_{r}0-mathbf {v} cdot mathbf {p} q_{r}mathbf {p} +0mathbf {v} +mathbf {v} times mathbf {p})s(q_{r}, -mathbf {v})\=&s(-mathbf {v} cdot mathbf {p} q_{r}mathbf {p} +mathbf {v} times mathbf {p})(q_{r}, -mathbf {v})\=&s(-mathbf {v} cdot mathbf {p} q_{r}-(q_{r}mathbf {p} +mathbf {v} times mathbf {p})cdot (-mathbf {v}), (-mathbf {v} cdot mathbf {p})(-mathbf {v})+q_{r}(q_{r}mathbf {p} +mathbf {v} times mathbf {p})+(q_{r}mathbf {p} +mathbf {v} times mathbf {p})times (-mathbf {v}))\=&sleft(-mathbf {v} cdot mathbf {p} q_{r}+q_{r}mathbf {v} cdot mathbf {p} mathbf {v} left(mathbf {v} cdot mathbf {p} right)+q_{r}^{2}mathbf {p} +q_{r}mathbf {v} times mathbf {p} +mathbf {v} times left(q_{r}mathbf {p} +mathbf {v} times mathbf {p} right)right)\=&left(0, sleft(mathbf {v} otimes mathbf {v} +q_{r}^{2}mathbf {I} +2q_{r}[mathbf {v} ]_{times }+[mathbf {v} ]_{times }^{2}right)mathbf {p} right),end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/791f3ce917350217ce39c6d61647940686c183f3)


![{displaystyle [mathbf {v} ]_{times }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eb8c75c76fcc67f0d13e3298d0b6de20a0c1254e)



![{displaystyle sleft(mathbf {v} otimes mathbf {v} +q_{r}^{2}mathbf {I} +2q_{r}[mathbf {v} ]_{times }+[mathbf {v} ]_{times }^{2}right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/af9cc39b5fe69b350b9203c4f82dabeb799e0e3d)


![{displaystyle {begin{aligned}(a_{x},a_{y},a_{z})={}&{frac {(q_{i},q_{j},q_{k})}{sqrt {q_{i}^{2}+q_{j}^{2}+q_{k}^{2}}}}\[2pt]theta =2operatorname {atan2} &left({sqrt {q_{i}^{2}+q_{j}^{2}+q_{k}^{2}}},,q_{r}right),end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc1d62fe7285e7371d40e848e6bdfca990367d8d)
















![{displaystyle {begin{aligned}{frac {partial mathbf {p'} }{partial mathbf {q} }}equiv left[{frac {partial mathbf {p'} }{partial q_{0}}},{frac {partial mathbf {p'} }{partial q_{x}}},{frac {partial mathbf {p'} }{partial q_{y}}},{frac {partial mathbf {p'} }{partial q_{z}}}right]=left[mathbf {pq} -(mathbf {pq})^{*},(mathbf {pqi})^{*}-mathbf {pqi}(mathbf {pqj})^{*}-mathbf {pqj}(mathbf {pqk})^{*}-mathbf {pqk} right].end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/559fc109c72845625b201ccfa99036aa226cc204)
















![{displaystyle {begin{aligned}{vec {v}}'&={vec {v}}cos ^{2}{frac {alpha }{2}}+left({vec {u}}{vec {v}}-{vec {v}}{vec {u}}right)sin {frac {alpha }{2}}cos {frac {alpha }{2}}-{vec {u}}{vec {v}}{vec {u}}sin ^{2}{frac {alpha }{2}}\[6pt]&={vec {v}}cos ^{2}{frac {alpha }{2}}+2left({vec {u}}times {vec {v}}right)sin {frac {alpha }{2}}cos {frac {alpha }{2}}-left(left({vec {u}}times {vec {v}}right)-left({vec {u}}cdot {vec {v}}right)right){vec {u}}sin ^{2}{frac {alpha }{2}}\[6pt]&={vec {v}}cos ^{2}{frac {alpha }{2}}+2left({vec {u}}times {vec {v}}right)sin {frac {alpha }{2}}cos {frac {alpha }{2}}-left(left({vec {u}}times {vec {v}}right){vec {u}}-left({vec {u}}cdot {vec {v}}right){vec {u}}right)sin ^{2}{frac {alpha }{2}}\[6pt]&={vec {v}}cos ^{2}{frac {alpha }{2}}+2left({vec {u}}times {vec {v}}right)sin {frac {alpha }{2}}cos {frac {alpha }{2}}-left(left(left({vec {u}}times {vec {v}}right)times {vec {u}}-left({vec {u}}times {vec {v}}right)cdot {vec {u}}right)-left({vec {u}}cdot {vec {v}}right){vec {u}}right)sin ^{2}{frac {alpha }{2}}\[6pt]&={vec {v}}cos ^{2}{frac {alpha }{2}}+2left({vec {u}}times {vec {v}}right)sin {frac {alpha }{2}}cos {frac {alpha }{2}}-left(left({vec {v}}-left({vec {u}}cdot {vec {v}}right){vec {u}}right)-0-left({vec {u}}cdot {vec {v}}right){vec {u}}right)sin ^{2}{frac {alpha }{2}}\[6pt]&={vec {v}}cos ^{2}{frac {alpha }{2}}+2left({vec {u}}times {vec {v}}right)sin {frac {alpha }{2}}cos {frac {alpha }{2}}-left({vec {v}}-2{vec {u}}left({vec {u}}cdot {vec {v}}right)right)sin ^{2}{frac {alpha }{2}}\[6pt]&={vec {v}}cos ^{2}{frac {alpha }{2}}+2left({vec {u}}times {vec {v}}right)sin {frac {alpha }{2}}cos {frac {alpha }{2}}-{vec {v}}sin ^{2}{frac {alpha }{2}}+2{vec {u}}left({vec {u}}cdot {vec {v}}right)sin ^{2}{frac {alpha }{2}}\[6pt]&={vec {v}}left(cos ^{2}{frac {alpha }{2}}-sin ^{2}{frac {alpha }{2}}right)+left({vec {u}}times {vec {v}}right)left(2sin {frac {alpha }{2}}cos {frac {alpha }{2}}right)+{vec {u}}left({vec {u}}cdot {vec {v}}right)left(2sin ^{2}{frac {alpha }{2}}right)\[6pt]end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/211d8613a1a8f990e93433cd4bd10937a2197eca)
![{displaystyle {begin{aligned}{vec {v}}'&={vec {v}}left(cos ^{2}{frac {alpha }{2}}-sin ^{2}{frac {alpha }{2}}right)+left({vec {u}}times {vec {v}}right)left(2sin {frac {alpha }{2}}cos {frac {alpha }{2}}right)+{vec {u}}left({vec {u}}cdot {vec {v}}right)left(2sin ^{2}{frac {alpha }{2}}right)\[6pt]&={vec {v}}cos alpha +left({vec {u}}times {vec {v}}right)sin alpha +{vec {u}}left({vec {u}}cdot {vec {v}}right)left(1-cos alpha right)\[6pt]&={vec {v}}cos alpha +left({vec {u}}times {vec {v}}right)sin alpha +{vec {u}}left({vec {u}}cdot {vec {v}}right)-{vec {u}}left({vec {u}}cdot {vec {v}}right)cos alpha \[6pt]&=left({vec {v}}-{vec {u}}left({vec {u}}cdot {vec {v}}right)right)cos alpha +left({vec {u}}times {vec {v}}right)sin alpha +{vec {u}}left({vec {u}}cdot {vec {v}}right)\[6pt]&={vec {v}}_{bot }cos alpha +left({vec {u}}times {vec {v}}right)sin alpha +{vec {v}}_{|}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/48bf26328d7a60ea06272e628ae4514076e0659a)








![{displaystyle {begin{aligned}mathbf {p} '_{text{alt}}={}&(mathbf {v} otimes mathbf {v} +q_{r}^{2}mathbf {I} mathbin {color {red}mathbf {-} } 2q_{r}[mathbf {v} ]_{times }+[mathbf {v} ]_{times }^{2})mathbf {p} &{text{(Alternative convention, usage discouraged!)}}\=& (mathbf {I} mathbin {color {red}mathbf {-} } 2q_{r}[mathbf {v} ]_{times }+2[mathbf {v} ]_{times }^{2})mathbf {p} &end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3750c56481e794e3fa99936110fba444b5c23188)
![{displaystyle {begin{aligned}mathbf {R} _{alt}&=mathbf {I} mathbin {color {red}mathbf {-} } 2q_{r}[mathbf {v} ]_{times }+2[mathbf {v} ]_{times }^{2}qquad {text{(Alternative convention, usage discouraged!)}}\&={begin{bmatrix}1-2s(q_{j}^{2}+q_{k}^{2})&2(q_{i}q_{j}+q_{k}q_{r})&2(q_{i}q_{k}-q_{j}q_{r})\2(q_{i}q_{j}-q_{k}q_{r})&1-2s(q_{i}^{2}+q_{k}^{2})&2(q_{j}q_{k}+q_{i}q_{r})\2(q_{i}q_{k}+q_{j}q_{r})&2(q_{j}q_{k}-q_{i}q_{r})&1-2s(q_{i}^{2}+q_{j}^{2})end{bmatrix}}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d28f0e656b8b25de89fbb55b260e7761dd7d38cf)














![{displaystyle {begin{aligned}mathbf {z} _{rm {l}}{vec {v}}mathbf {z} _{rm {r}}&={begin{pmatrix}1&-dt_{ab}&-dt_{ac}&-dt_{ad}\dt_{ab}&1&-dt_{bc}&-dt_{bd}\dt_{ac}&dt_{bc}&1&-dt_{cd}\dt_{ad}&dt_{bd}&dt_{cd}&1end{pmatrix}}{begin{pmatrix}w\x\y\zend{pmatrix}}\[3pt]mathbf {z} _{rm {l}}&=1+{dt_{ab}+dt_{cd} over 2}i+{dt_{ac}-dt_{bd} over 2}j+{dt_{ad}+dt_{bc} over 2}k\[3pt]mathbf {z} _{rm {r}}&=1+{dt_{ab}-dt_{cd} over 2}i+{dt_{ac}+dt_{bd} over 2}j+{dt_{ad}-dt_{bc} over 2}kend{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d357c8e70a12570ad6275ed837bedb837306d11e)