Cuantización (procesamiento de señales)

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Proceso de mapeo de un conjunto continuo a un conjunto contable

Cuantización, en matemáticas y procesamiento de señales digitales, es el proceso de asignar valores de entrada de un conjunto grande (a menudo un conjunto continuo) a valores de salida en un conjunto más pequeño (contable), a menudo con un número finito de elementos. El redondeo y el truncamiento son ejemplos típicos de procesos de cuantificación. La cuantificación está involucrada hasta cierto punto en casi todo el procesamiento de señales digitales, ya que el proceso de representar una señal en forma digital generalmente implica redondeo. La cuantificación también forma el núcleo de esencialmente todos los algoritmos de compresión con pérdida.

La diferencia entre un valor de entrada y su valor cuantificado (como el error de redondeo) se denomina error de cuantificación. Un dispositivo o función algorítmica que realiza la cuantificación se denomina cuantificador. Un convertidor de analógico a digital es un ejemplo de cuantificador.

Ejemplo

Por ejemplo, redondeando un número real $x$ al valor entero más cercano forma un tipo muy básico de cuarentena – un uniforme Uno. Un típicomitad del pan) cuadrante uniforme con una cuantificación tamaño del paso igual a algún valor $Delta$ se puede expresar como

{displaystyle Q(x)=Delta cdot leftlfloor {frac {x}{Delta }}+{frac {1}{2}}rightrfloor }

donde la notación $lfloor rfloor$ denota la función del suelo.

La propiedad esencial de un cuantizador es tener un conjunto contable de posibles miembros de valor de salida más pequeño que el conjunto de posibles valores de entrada. Los miembros del conjunto de valores de salida pueden tener valores enteros, racionales o reales. Para el redondeo simple al entero más cercano, el tamaño del paso $Delta$ es igual a 1. Con $Delta =1$ o con $Delta$ igual a cualquier otro valor entero, este cuantificador tiene entradas de valor real y salidas de valor entero.

Cuando el tamaño del paso de cuantificación (Δ) es pequeño en relación con la variación en la señal siendo cuantificada, es relativamente simple mostrar que el error medio cuadrado producido por tal operación de redondeo será aproximadamente $Delta ^{2}/12$ . El error medio cuadrado también se llama cuantización ruido. Añadiendo un poco a las mitades de cuarentena el valor de Δ, que reduce la potencia de ruido por el factor 1⁄4. En términos de decibeles, el cambio de potencia de ruido es ${displaystyle scriptstyle 10cdot log _{10}(1/4) approx -6 mathrm {dB}.}$

Debido a que el conjunto de los posibles valores de salida de un cuantizador es contable, cualquier cuantizador puede ser descompuesto en dos etapas distintas, que se pueden denominar el clasificación etapa (o cuantificación avanzada y la etapa reconstrucción etapa (o cuantificación inversa etapa), donde la etapa de clasificación mapea el valor de entrada a un entero índice de cuantificación $k$ y la etapa de reconstrucción mapas el índice $k$ a la Valor de la reconstrucción $y_{k}$ que es la aproximación de salida del valor de entrada. Por ejemplo, el cuantificador uniforme descrito anteriormente, la etapa de cuantificación avanzada puede expresarse como

k=leftlfloor {frac {x}{Delta }}+{frac {1}{2}}rightrfloor

y la etapa de reconstrucción para este cuantificador de ejemplo es simplemente

y_{k}=kcdot Delta

Esta descomposición es útil para el diseño y análisis del comportamiento de cuantificación, e ilustra cómo los datos cuantificados se pueden comunicar a través de un canal de comunicación: un codificador de fuente puede realizar la etapa de cuantificación directa y enviar la indexar información a través de un canal de comunicación, y un decodificador puede realizar la etapa de reconstrucción para producir la aproximación de salida de los datos de entrada originales. En general, la etapa de cuantificación directa puede usar cualquier función que mapee los datos de entrada al espacio entero de los datos del índice de cuantificación, y la etapa de cuantificación inversa puede conceptualmente (o literalmente) ser una operación de búsqueda de tabla para mapear cada índice de cuantificación a un valor de reconstrucción correspondiente. Esta descomposición en dos etapas se aplica igualmente bien a cuantificadores vectoriales como escalares.

Propiedades matemáticas

Debido a que la cuantificación es un mapeo de muchos a pocos, es un proceso inherentemente no lineal e irreversible (es decir, debido a que el mismo valor de salida es compartido por múltiples valores de entrada, es imposible, en general, recuperar el valor exacto valor de entrada cuando se da sólo el valor de salida).

El conjunto de posibles valores de entrada puede ser infinitamente grande y posiblemente continuo y, por lo tanto, incontable (como el conjunto de todos los números reales, o todos los números reales dentro de un rango limitado). El conjunto de posibles valores de salida puede ser finito o contablemente infinito. Los conjuntos de entrada y salida involucrados en la cuantificación se pueden definir de una manera bastante general. Por ejemplo, la cuantificación vectorial es la aplicación de la cuantificación a datos de entrada multidimensionales (con valores vectoriales).

Tipos

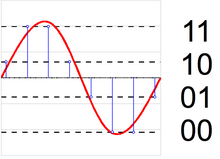
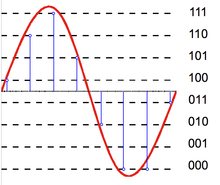
Convertidor de analógico a digital

Un convertidor de analógico a digital (ADC) se puede modelar como dos procesos: muestreo y cuantificación. El muestreo convierte una señal de voltaje variable en el tiempo en una señal de tiempo discreto, una secuencia de números reales. La cuantificación reemplaza cada número real con una aproximación de un conjunto finito de valores discretos. Por lo general, estos valores discretos se representan como palabras de punto fijo. Aunque es posible cualquier número de niveles de cuantificación, las longitudes de palabra comunes son de 8 bits (256 niveles), 16 bits (65 536 niveles) y 24 bits (16,8 millones de niveles). La cuantificación de una secuencia de números produce una secuencia de errores de cuantificación que a veces se modela como una señal aleatoria aditiva llamada ruido de cuantificación debido a su comportamiento estocástico. Cuantos más niveles utiliza un cuantificador, menor es su potencia de ruido de cuantificación.

Optimización de tasa de distorsión

La tasa optimizada de distorsión de tasa se encuentra en la codificación fuente para algoritmos de compresión de datos con pérdidas, donde el propósito es administrar la distorsión dentro de los límites de la tasa de bits admitida por un canal de comunicación o medio de almacenamiento. El análisis de la cuantificación en este contexto implica estudiar la cantidad de datos (normalmente medidos en dígitos o bits o velocidad de bits) que se utiliza para representar la salida del cuantificador, y estudiar la pérdida de precisión que se produce. introducido por el proceso de cuantificación (que se conoce como la distorsión).

Cuantificadores uniformes de bandas medias y bandas medias

La mayoría de los cuantificadores uniformes para datos de entrada firmados se pueden clasificar en uno de dos tipos: mediana altura y mediana banda de rodadura. La terminología se basa en lo que sucede en la región alrededor del valor 0 y utiliza la analogía de ver la función de entrada-salida del cuantificador como una escalera. Los cuantificadores de huella media tienen un nivel de reconstrucción de valor cero (correspondiente a una peldaño de una escalera), mientras que los cuantificadores de contrahuella media tienen un umbral de clasificación de valor cero (correspondiente a una contrahuella de una escalera).

La cuantización de la mitad de la banda de rodadura implica el redondeo. Las fórmulas para la cuantificación uniforme de la mitad de la banda de rodadura se proporcionan en la sección anterior.

Did you mean:

Mid-riser quantization involves truncation. The input-output formula for a mid-rise uniform quantizer is given by:

Q(x)=Delta cdot left(leftlfloor {frac {x}{Delta }}rightrfloor +{frac {1}{2}}right)

donde la regla de clasificación viene dada por

k=leftlfloor {frac {x}{Delta }}rightrfloor

y la regla de reconstrucción es

y_{k}=Delta cdot left(k+{tfrac {1}{2}}right)

Tenga en cuenta que los cuantificadores uniformes de media altura no tienen un valor de salida cero: su magnitud de salida mínima es la mitad del tamaño del paso. Por el contrario, los cuantificadores de la mitad de la banda de rodadura tienen un nivel de salida cero. Para algunas aplicaciones, tener una representación de señal de salida cero puede ser una necesidad.

En general, es posible que un cuantificador de bandas medias o bandas medias no sea realmente un cuantificador uniforme; es decir, es posible que el tamaño de los intervalos de clasificación del cuantificador no sea el mismo. o el espacio entre sus posibles valores de salida puede no ser el mismo. La característica distintiva de un cuantificador de media altura es que tiene un valor de umbral de clasificación que es exactamente cero, y la característica distintiva de un cuantificador de media banda es que tiene un valor de reconstrucción que es exactamente cero.

Cuantificadores de zona muerta

A quantizer de la zona muerta es un tipo de cuarentenizador medio con comportamiento simétrico alrededor de 0. La región alrededor del valor de salida cero de tal cuantizador se denomina el zona muerta o muerto. La zona muerta a veces puede servir el mismo propósito que una puerta de ruido o función de squelch. Especialmente para aplicaciones de compresión, la zona muerta se puede dar un ancho diferente al de los otros pasos. Para un cuantizador de otro tipo, el ancho de la zona muerta se puede establecer a cualquier valor $w$ utilizando la regla de cuantificación avanzada

k=operatorname {sgn}(x)cdot max left(0,leftlfloor {frac {left|xright|-w/2}{Delta }}+1rightrfloor right)

donde la función $operatorname {sgn}$ () es la función de signo (también conocida como signum función). La norma general de reconstrucción de un cuantizador de zona muerta es dada por

y_{k}=operatorname {sgn}(k)cdot left({frac {w}{2}}+Delta cdot (|k|-1+r_{k})right)

Donde $r_{k}$ es un valor offset de reconstrucción en el rango de 0 a 1 como una fracción del tamaño del paso. Normalmente, $0leq r_{k}leq {tfrac {1}{2}}$ Cuando se cuantifican los datos de entrada con una función de densidad de probabilidad típica (PDF) que es simétrica alrededor de cero y alcanza su valor máximo a cero (como un PDF Gaussian, Laplacian o Gaussian generalizado). Aunque $r_{k}$ puede depender de $k$ en general, y puede ser elegido para cumplir con la condición de óptimaidad descrita a continuación, es a menudo simplemente fijado a una constante, como ${tfrac {1}{2}}$ . (Nota eso en esta definición, $y_{0}=0$ debido a la definición de la $operatorname {sgn}$ () función, así que $r_{0}$ no tiene efecto.)

Un caso especial muy comúnmente utilizado (por ejemplo, el esquema utilizado típicamente en contabilidad financiera y matemáticas elementales) es establecer $w=Delta$ y $r_{k}={tfrac {1}{2}}$ para todos $k$ . En este caso, el cuarentenizador de zona muerta es también un cuarentena uniforme, ya que la zona muerta central de este cuarentena tiene el mismo ancho que todos sus otros pasos, y todos sus valores de reconstrucción están igualmente espaciados.

Características de ruido y error

Modelo de ruido aditivo

Una suposición común para el análisis del error de cuantificación es que afecta a un sistema de procesamiento de señales de una manera similar a la del ruido aditivo blanco – teniendo correlación insignificante con la señal y una densidad espectral de potencia aproximadamente plana. El modelo de ruido aditivo se utiliza comúnmente para el análisis de los efectos de errores de cuantificación en los sistemas de filtrado digital, y puede ser muy útil en dicho análisis. Se ha demostrado que es un modelo válido en casos de cuantificación de alta resolución (pequeña) $Delta$ relativo a la fuerza de la señal) con PDF liso.

El comportamiento del ruido aditivo no siempre es una suposición válida. El error de cuantificación (para los cuantificadores definidos como se describe aquí) está relacionado de manera determinista con la señal y no es completamente independiente de ella. Por lo tanto, las señales periódicas pueden crear ruido de cuantificación periódica. Y en algunos casos puede incluso provocar la aparición de ciclos límite en los sistemas de procesamiento de señales digitales. Una forma de garantizar la independencia efectiva del error de cuantificación de la señal de origen es realizar una cuantificación interpolada (a veces con formación de ruido), que implica agregar señales aleatorias (o pseudoaleatorias) ruido a la señal antes de la cuantificación.

Modelos de error de cuantificación

En el caso típico, la señal original es mucho más grande que un bit menos significativo (LSB). Cuando este es el caso, el error de cuantificación no se correlaciona significativamente con la señal, y tiene una distribución aproximadamente uniforme. Cuando el redondeo se utiliza para cuantificar, el error de cuantización tiene una media de cero y el valor cuadrado medio raíz (RMS) es la desviación estándar de esta distribución, dada por $scriptstyle {frac {1}{sqrt {12}}}mathrm {LSB} approx 0.289,mathrm {LSB}$ . Cuando se utiliza la truncación, el error tiene una media no cero de $scriptstyle {frac {1}{2}}mathrm {LSB}$ y el valor RMS $scriptstyle {frac {1}{sqrt {3}}}mathrm {LSB}$ . Aunque el redondeo produce menos error RMS que la truncación, la diferencia sólo se debe al término estático (DC) $scriptstyle {frac {1}{2}}mathrm {LSB}$ . Los valores de RMS del error de AC son exactamente los mismos en ambos casos, por lo que no hay ventaja especial de redondear la truncación en situaciones en las que se puede ignorar el término DC del error (como en sistemas acoplados de AC). En cualquier caso, la desviación estándar, como porcentaje del rango de señal completo, cambia por un factor de 2 para cada cambio de 1 bit en el número de bits de cuantificación. Por lo tanto, la relación potencial de potencia de señal a centralización cambia en 4, o ${displaystyle scriptstyle 10cdot log _{10}(4)}$ , aproximadamente 6 dB por bit.

A amplitudes más bajas, el error de cuantificación depende de la señal de entrada, lo que genera distorsión. Esta distorsión se crea después del filtro anti-aliasing, y si estas distorsiones están por encima de la mitad de la frecuencia de muestreo, regresarán a la banda de interés. Para hacer que el error de cuantificación sea independiente de la señal de entrada, la señal se difumina añadiendo ruido a la señal. Esto reduce ligeramente la relación señal/ruido, pero puede eliminar por completo la distorsión.

Modelo de ruido de cuantificación

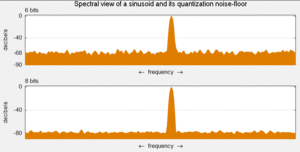
El ruido de cuantificación es un modelo de error de cuantificación introducido por la cuantificación en el ADC. Es un error de redondeo entre el voltaje de entrada analógica al ADC y el valor digitalizado de salida. El ruido no es lineal y depende de la señal. Se puede modelar de varias maneras diferentes.

En un ADC ideal, donde el error de cuantificación se distribuye uniformemente entre −1/2 LSB y +1/2 LSB, y la señal tiene una distribución uniforme que cubre todos los niveles de cuantificación, la relación señal-ruido de cuantificación (SQNR) se puede calcular a partir de

mathrm {SQNR} =20log _{10}(2^{Q})approx 6.02cdot Q mathrm {dB} ,!

donde Q es el número de bits de cuantificación.

Las señales de prueba más comunes que cumplen con esto son las ondas triangulares de amplitud completa y las ondas de diente de sierra.

Por ejemplo, un ADC de 16 bits tiene una relación señal/ruido de cuantificación máxima de 6,02 × 16 = 96,3 dB.

Cuando la señal de entrada es una onda sinusoidal de amplitud completa, la distribución de la señal ya no es uniforme y, en cambio, la ecuación correspondiente es

mathrm {SQNR} approx 1.761+6.02cdot Q mathrm {dB} ,!

Aquí, se vuelve a suponer que el ruido de cuantificación se distribuye uniformemente. Este es el caso cuando la señal de entrada tiene una gran amplitud y un amplio espectro de frecuencia. En este caso, un ADC de 16 bits tiene una relación señal/ruido máxima de 98,09 dB. La diferencia de 1,761 en la relación señal-ruido solo se produce debido a que la señal es una onda sinusoidal a gran escala en lugar de un triángulo o un diente de sierra.

Para señales complejas en ADC de alta resolución, este es un modelo preciso. Para ADC de baja resolución, señales de bajo nivel en ADC de alta resolución y para formas de onda simples, el ruido de cuantificación no se distribuye uniformemente, lo que hace que este modelo sea inexacto. En estos casos, la distribución del ruido de cuantificación se ve fuertemente afectada por la amplitud exacta de la señal.

Los cálculos son relativos a la entrada a escala completa. Para señales más pequeñas, la distorsión de cuantificación relativa puede ser muy grande. Para eludir este problema, se puede usar compansión analógica, pero esto puede introducir distorsión.

Diseño

Distorsión granular y distorsión de sobrecarga

A menudo el diseño de un cuarentena implica apoyar sólo una gama limitada de posibles valores de salida y realizar clipping para limitar la salida a este rango cuando la entrada supera el rango soportado. El error introducido por este clipping se conoce como sobrecarga distorsión. Dentro de los límites extremos de la gama soportada, la cantidad de espaciamiento entre los valores de salida seleccionables de un cuantificador se denomina su granularidad, y el error introducido por este espaciado se conoce como granular distorsión. Es común que el diseño de un cuarentena implique determinar el equilibrio adecuado entre la distorsión granular y la distorsión de sobrecarga. Para un número determinado de posibles valores de producción, reducir la distorsión granular promedio puede implicar aumentar la distorsión promedio de sobrecarga, y viceversa. Una técnica para controlar la amplitud de la señal (o, equivalentemente, el tamaño del paso de cuantificación $Delta$ ) para lograr el equilibrio adecuado es el uso de control automático de ganancia (AGC). Sin embargo, en algunos diseños de cuarentena, los conceptos de error granular y error de sobrecarga no pueden aplicarse (por ejemplo, para un cuarentena con un rango limitado de datos de entrada o con un conjunto contablemente infinito de valores de salida seleccionables).

Diseño de cuantificador de tasa-distorsión

Un cuantificador escalar, que realiza una operación de cuantificación, normalmente se puede descomponer en dos etapas:

Clasificación: Un proceso que clasifica el rango de señal de entrada en $M$ no superposición intervalos ${I_{k}}_{k=1}^{M}$ , definiendo $M-1$ frontera de la decisión valores ${b_{k}}_{k=1}^{M-1}$ , tal que $I_{k}=[b_{k-1}~,~b_{k})$ para $k=1,2,ldotsM$ , con los límites extremos definidos $b_{0}=-infty$ y $b_{M}=infty$ . Todas las entradas $x$ que caen en un intervalo determinado $I_{k}$ están asociados con el mismo índice de cuantificación $k$ .
Reconstrucción: Cada intervalo $I_{k}$ está representado por un Valor de la reconstrucción $y_{k}$ que implementa la cartografía $xin I_{k}Rightarrow y=y_{k}$ .

Estas dos etapas juntas comprenden la operación matemática de $y=Q(x)$ .

Se pueden aplicar técnicas de codificación entropía para comunicar los índices de cuantificación de un encoder fuente que realiza la etapa de clasificación a un decodificador que realiza la etapa de reconstrucción. Una manera de hacer esto es asociar cada índice de cuantificación $k$ con un código binario $c_{k}$ . Una consideración importante es el número de bits utilizados para cada palabra clave, denotado aquí por $mathrm {length} (c_{k})$ . Como resultado, el diseño de un $M$ - cuantificador de nivel y un conjunto asociado de palabras clave para comunicar sus valores índice requiere encontrar los valores de ${b_{k}}_{k=1}^{M-1}$ , ${c_{k}}_{k=1}^{M}$ y ${y_{k}}_{k=1}^{M}$ que satisface óptimamente un conjunto seleccionado de limitaciones de diseño, como tasa de bits $R$ y distorsión $D$ .

Asumiendo que una fuente de información $S$ produce variables aleatorias $X$ con un PDF asociado $f(x)$ , la probabilidad $p_{k}$ que la variable aleatoria cae dentro de un intervalo de cuantificación particular $I_{k}$ es dado por:

p_{k}=P[xin I_{k}]=int _{b_{k-1}}^{b_{k}}f(x)dx

La tasa de bits resultante $R$ , en unidades de bits promedio por valor cuantificado, para este cuantificador se puede derivar de la siguiente manera:

R=sum _{k=1}^{M}p_{k}cdot mathrm {length} (c_{k})=sum _{k=1}^{M}mathrm {length} (c_{k})int _{b_{k-1}}^{b_{k}}f(x)dx

Si se supone que la distorsión se mide por el error cuadrático medio, la distorsión D viene dada por:

D=E[(x-Q(x))^{2}]=int _{-infty }^{infty }(x-Q(x))^{2}f(x)dx=sum _{k=1}^{M}int _{b_{k-1}}^{b_{k}}(x-y_{k})^{2}f(x)dx

Una observación clave es que la tasa $R$ depende de los límites de decisión ${b_{k}}_{k=1}^{M-1}$ y las longitudes de la palabra clave ${mathrm {length} (c_{k})}_{k=1}^{M}$ , mientras que la distorsión $D$ depende de los límites de decisión ${b_{k}}_{k=1}^{M-1}$ y los niveles de reconstrucción ${y_{k}}_{k=1}^{M}$ .

Después de definir estas dos métricas de rendimiento para el cuantificador, una formulación típica de distorsión de velocidad para un problema de diseño de cuantificador se puede expresar de dos maneras:

Dado un límite máximo de distorsión $Dleq D_{max }$ , minimizar la tasa de bits $R$
Dado un límite máximo de velocidad de bits $Rleq R_{max }$ , minimizar la distorsión $D$

A menudo la solución a estos problemas puede ser equivalente (o aproximadamente) expresada y resuelta mediante la conversión de la formulación al problema sin restricciones $min left{D+lambda cdot Rright}$ donde el multiplicador Lagrange $lambda$ es una constante no negativa que establece el equilibrio adecuado entre la tasa y la distorsión. Resolver el problema sin restricciones equivale a encontrar un punto en el casco convexo de la familia de soluciones a una formulación limitada equivalente del problema. Sin embargo, encontrar una solución – especialmente una solución de forma cerrada – a cualquiera de estas tres formulaciones de problemas puede ser difícil. Las soluciones que no requieren técnicas de optimización iterativa multidimensional se han publicado sólo para tres PDFs: las distribuciones uniformes, exponenciales y laplacianas. Se pueden utilizar enfoques de optimización iterativa para encontrar soluciones en otros casos.

Note que los valores de reconstrucción ${y_{k}}_{k=1}^{M}$ afectan sólo la distorsión – no afectan la tasa de bits – y que cada individuo $y_{k}$ hace una contribución separada $d_{k}$ a la distorsión total como se muestra a continuación:

D=sum _{k=1}^{M}d_{k}

dónde

d_{k}=int _{b_{k-1}}^{b_{k}}(x-y_{k})^{2}f(x)dx

Esta observación se puede utilizar para facilitar el análisis – dado el conjunto de ${b_{k}}_{k=1}^{M-1}$ valores, el valor de cada $y_{k}$ se puede optimizar por separado para minimizar su contribución a la distorsión $D$ .

Para el criterio de distorsión del error medio cuadrado, se puede demostrar fácilmente que el conjunto óptimo de valores de reconstrucción ${y_{k}^{*}}_{k=1}^{M}$ se da estableciendo el valor de reconstrucción $y_{k}$ dentro de cada intervalo $I_{k}$ al valor esperado condicional (también conocido como centroide) dentro del intervalo, dado por:

y_{k}^{*}={frac {1}{p_{k}}}int _{b_{k-1}}^{b_{k}}xf(x)dx

El uso de técnicas de codificación entropía suficientemente bien diseñadas puede resultar en el uso de una tasa de bits cercana al verdadero contenido de información de los índices ${k}_{k=1}^{M}$ , tal que efectivamente

mathrm {length} (c_{k})approx -log _{2}left(p_{k}right)

y por lo tanto

R=sum _{k=1}^{M}-p_{k}cdot log _{2}left(p_{k}right)

El uso de esta aproximación puede permitir que el problema de diseño de codificación entropía se separe del diseño del propio cuantizador. Técnicas modernas de codificación entropía, como codificación aritmética, pueden alcanzar tasas de bits muy cercanas a la verdadera entropía de una fuente, dadas las probabilidades conocidas (o calculadas de forma adaptativa) ${p_{k}}_{k=1}^{M}$ .

En algunos diseños, en lugar de optimizar un número determinado de regiones de clasificación $M$ , el problema de diseño de cuarentena puede incluir la optimización del valor $M$ también. Para algunos modelos de fuentes probabilistas, el mejor rendimiento se puede lograr cuando $M$ se acerca al infinito.

Ignorar la restricción de entropía: cuantización de Lloyd-Max

En la formulación anterior, si se descuida la limitación de la tasa de bits estableciendo $lambda$ igual a 0, o equivalentemente si se supone que un código de longitud fija (FLC) se utilizará para representar los datos cuantificados en lugar de un código de longitud variable (o alguna otra tecnología de codificación entropía como codificación aritmética que es mejor que un FLC en el sentido de la distorsión de la tasa), el problema de optimización reduce a minimización de la distorsión $D$ solo.

Los índices producidos por un $M$ - nivel quantizer se puede codificar usando un código de longitud fijo usando $R=lceil log _{2}Mrceil$ bits/symbol. Por ejemplo, cuando $M=$ 256 niveles, la tasa de bits FLC $R$ es 8 bits/symbol. Por esta razón, a veces se ha llamado un cuarentena de 8 bits. Sin embargo, el uso de un FLC elimina la mejora de compresión que se puede obtener mediante el uso de una mejor codificación entropía.

Asumiendo un FLC con $M$ los niveles, el problema de minimización de la tasa–distorsión puede reducirse a la minimización de la distorsión. El problema reducido se puede decir de la siguiente manera: dada una fuente $X$ con PDF $f(x)$ y la limitación que el cuarentena debe utilizar sólo $M$ regiones de clasificación, encontrar los límites de decisión ${b_{k}}_{k=1}^{M-1}$ y niveles de reconstrucción ${y_{k}}_{k=1}^{M}$ para minimizar la distorsión resultante

D=E[(x-Q(x))^{2}]=int _{-infty }^{infty }(x-Q(x))^{2}f(x)dx=sum _{k=1}^{M}int _{b_{k-1}}^{b_{k}}(x-y_{k})^{2}f(x)dx=sum _{k=1}^{M}d_{k}

Encontrar una solución óptima al problema anterior resulta en un cuantizador llamado a veces una solución MMSQE (mínimo error de cuantificación media cuadrada) y el cuantizador resultante optimizado con PDF (no uniforme) se denomina un cuantizador como un error de cuantificación. Lloyd-Max quantizer, nombrado por dos personas que desarrollaron métodos iterativos independientemente para resolver los dos conjuntos de ecuaciones simultáneas resultantes de ${partial D/partial b_{k}}=0$ y ${partial D/partial y_{k}}=0$ , como sigue:

{partial D over partial b_{k}}=0Rightarrow b_{k}={y_{k}+y_{k+1} over 2}

que coloca cada umbral en el punto medio entre cada par de valores de reconstrucción, y

{partial D over partial y_{k}}=0Rightarrow y_{k}={int _{b_{k-1}}^{b_{k}}xf(x)dx over int _{b_{k-1}}^{b_{k}}f(x)dx}={frac {1}{p_{k}}}int _{b_{k-1}}^{b_{k}}xf(x)dx

que coloca cada valor de reconstrucción en el centroide (valor esperado condicional) de su intervalo de clasificación asociado.

El algoritmo del método I de Lloyd, descrito originalmente en 1957, se puede generalizar de forma sencilla para aplicarlo a datos vectoriales. Esta generalización da como resultado los métodos de optimización del clasificador Linde-Buzo-Gray (LBG) o k-means. Además, la técnica se puede generalizar aún más de forma directa para incluir también una restricción de entropía para datos vectoriales.

Cuantificación uniforme y aproximación de 6 dB/bit

El cuantizador Lloyd-Max es en realidad un cuantizador uniforme cuando el PDF de entrada se distribuye uniformemente en el rango $[y_{1}-Delta /2,~y_{M}+Delta /2)$ . Sin embargo, para una fuente que no tenga una distribución uniforme, el cuantificador mínimo de distorsión puede no ser un cuantificador uniforme. El análisis de un cuantificador uniforme aplicado a una fuente distribuida de forma uniforme puede resumirse en lo siguiente:

Una fuente simétrica X se puede modelar con ${displaystyle f(x)={tfrac {1}{2X_{max }}}}$ , para ${displaystyle xin [-X_{max },X_{max }]}$ y 0 en otro lugar. El tamaño del paso ${displaystyle Delta ={tfrac {2X_{max }}{M}}}$ y el ratio de ruido de señal a cuantización (SQNR) del cuantizador es

{rm {SQNR}}=10log _{10}{frac {sigma _{x}^{2}}{sigma _{q}^{2}}}=10log _{10}{frac {(MDelta)^{2}/12}{Delta ^{2}/12}}=10log _{10}M^{2}=20log _{10}M

Para un código de longitud fijo usando $N$ bits, $M=2^{N}$ , resultando en ${rm {SQNR}}=20log _{10}{2^{N}}=Ncdot (20log _{10}2)=Ncdot 6.0206,{rm {dB}}$ ,

o aproximadamente 6 dB por bit. Por ejemplo, $N$ =8 bits, $M$ =256 niveles y SQNR = 8×6 = 48 dB; y $N$ =16 bits, $M$ =65536 y SQNR = 16×6 = 96 dB. La propiedad de 6 dB mejora en SQNR para cada bit adicional utilizado en la cuantificación es una figura bien conocida de mérito. Sin embargo, debe usarse con cuidado: esta derivación es sólo para un cuantificador uniforme aplicado a una fuente uniforme. Para otros archivos PDF de origen y otros diseños de cuarentena, el SQNR puede ser un tanto diferente de los predichos por 6 dB/bit, dependiendo del tipo de PDF, el tipo de fuente, el tipo de cuarentena, y el rango de velocidad de bits de operación.

Sin embargo, es común suponer que para muchas fuentes, la pendiente de una función SQNR cuantizadora puede aproximarse a 6 dB/bit cuando se opera a una velocidad de bits suficientemente alta. A tasas de bits asintomáticamente altas, cortar el tamaño del paso en la mitad aumenta la tasa de bits aproximadamente 1 bit por muestra (porque se necesita 1 bit para indicar si el valor está en la mitad izquierda o derecha del intervalo de doble tamaño anterior) y reduce el error medio cuadrado por un factor de 4 (es decir, 6 dB) basado en el intervalo de doble tamaño anterior) $Delta ^{2}/12$ aproximación.

A tasas de bits asintóticamente altas, la aproximación de 6 dB/bit es compatible con muchos archivos PDF de origen mediante un análisis teórico riguroso. Además, la estructura del cuantificador escalar óptimo (en el sentido de tasa-distorsión) se aproxima a la de un cuantificador uniforme en estas condiciones.

En otros campos

Muchas cantidades físicas son realmente cuantificadas por entidades físicas. Los ejemplos de campos en los que se aplica esta limitación incluyen la electrónica (debido a los electrones), la óptica (debido a los fotones), la biología (debido al ADN), la física (debido a los límites de Planck) y la química (debido a las moléculas).

Contenido relacionado

Más resultados...