Cualquiera

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Tipo de partícula que ocurre sólo en sistemas bidimensionales

En física, un anyon es un tipo de cuasipartícula que se produce sólo en sistemas bidimensionales, con propiedades mucho menos restringidas que los dos tipos de partículas elementales estándar, fermiones y bosones. En general, la operación de intercambiar dos partículas idénticas, aunque puede provocar un cambio de fase global, no puede afectar a los observables. Los Anyons generalmente se clasifican como abelianos o no abelianos. Los anyons abelianos (detectados mediante dos experimentos en 2020) desempeñan un papel importante en el efecto Hall cuántico fraccionario. A partir de 2023, esta es un área activa de investigación; Utilizando un procesador superconductor, Google Quantum AI informó sobre el primer trenzado de anyons no abelianos en un artículo de arXiv de Andersen et al. en octubre de 2022, publicado posteriormente en Nature. En un artículo de arXiv publicado en mayo de 2023, Quantinuum informó sobre el trenzado no abeliano utilizando un procesador de iones atrapados.

Introducción

La mecánica estadística de grandes sistemas de muchos cuerpos obedece a las leyes descritas por las estadísticas de Maxwell-Boltzmann. La estadística cuántica es más complicada debido a los diferentes comportamientos de dos tipos diferentes de partículas llamadas fermiones y bosones. Citando una descripción reciente y sencilla:

En el mundo tridimensional en el que vivimos, sólo hay dos tipos de partículas: "fermiones", que se repelen unos a otros, y "hijos", que les gusta unirse. Un fermión comúnmente conocido es el electrón, que transporta electricidad; y un bosón comúnmente conocido es el fotón, que lleva luz. En el mundo bidimensional, sin embargo, hay otro tipo de partícula, el cualquiera, que no se comporta como un fermión o un bosón.

En un mundo bidimensional, dos objetos idénticos cambian su función de onda cuando intercambian lugares de maneras que no pueden suceder en la física tridimensional:

...en dos dimensiones, el intercambio de partículas idénticas dos veces no es equivalente a dejarlas solas. La función de onda de las partículas después de cambiar lugares dos veces puede diferir del original; las partículas con estadísticas de intercambio tan inusuales son conocidas como cualquiera. Por el contrario, en tres dimensiones, intercambiar partículas dos veces no puede cambiar su funcionamiento de onda, dejándonos con sólo dos posibilidades: bosones, cuya función de onda sigue siendo la misma incluso después de un solo intercambio, y fermions, cuyo intercambio sólo cambia el signo de su funcionamiento de onda.

Este proceso de intercambiar partículas idénticas, o de hacer girar una partícula alrededor de otra, se conoce con su nombre matemático como "trenzado". "Trenzado" dos anyons crean un registro histórico del evento, ya que sus funciones de onda modificadas "cuentan" el número de trenzas.

Microsoft ha invertido en investigaciones sobre anyons como base potencial para la computación cuántica topológica. Cualquiera que se rodeara entre sí ("trenzado") codificaría la información de una manera más sólida que otras posibles tecnologías de computación cuántica. Sin embargo, la mayor parte de la inversión en computación cuántica se basa en métodos que no utilizan a nadie.

Historia

Como tantas ideas profundas en la física, los fundamentos topológicos de cualquierones pueden ser rastreados de nuevo a Dirac
—Biedenharn at al., El Ancestro del Anyon

En 1977, dos físicos teóricos que trabajaban en la Universidad de Oslo, Jon Magne Leinaas y Jan Myrheim, demostraron que la clasificación tradicional de partículas como fermiones o bosones no se aplicaría si se las restringiera a moverse solo en dos dimensiones. Se esperaría que las partículas hipotéticas, al no ser ni bosones ni fermiones, exhibieran una amplia gama de propiedades previamente inesperadas. En 1982, Frank Wilczek publicó dos artículos que exploraban la estadística fraccionaria de cuasipartículas en dos dimensiones, dándoles el nombre de "anyons" para indicar que el cambio de fase tras la permutación puede tomar cualquier valor.

Daniel Tsui y Horst Störmer descubrieron el efecto Hall cuántico fraccionario en 1982. Las matemáticas desarrolladas por Wilczek resultaron útiles a Bertrand Halperin de la Universidad de Harvard para explicar algunos aspectos del mismo. Frank Wilczek, Dan Arovas y Robert Schrieffer verificaron esta afirmación en 1985 con un cálculo explícito que predijo que las partículas existentes en estos sistemas son en realidad cualquiera.

Abelianos

En la mecánica cuántica, y algunos sistemas estocásticos clásicos, partículas indistinguibles tienen la propiedad que intercambia los estados de partículas $i$ con partículas $j$ (symbolically ${displaystyle psi _{i}leftrightarrow psi _{j}{text{ for }}ineq j}$ ) no conduce a un estado mensurablemente diferente de muchos cuerpos.

En un sistema mecánico cuántico, por ejemplo, un sistema con dos partículas indistinguibles, con la partícula 1 en estado $psi _{1}$ y la partícula 2 en estado $psi _{2}$ , tiene estado ${displaystyle left|psi _{1}psi _{2}rightrangle }$ en la notación Dirac. Ahora supongamos que intercambiamos los estados de las dos partículas, entonces el estado del sistema sería ${displaystyle left|psi _{2}psi _{1}rightrangle }$ . Estos dos estados no deben tener una diferencia mensurable, por lo que deben ser el mismo vector, hasta un factor de fase:

{displaystyle left|psi _{1}psi _{2}rightrangle =e^{itheta }left|psi _{2}psi _{1}rightrangle.}

Aquí, $e^{itheta }$ es el factor de fase. En el espacio de tres o más dimensiones, el factor de fase es $1$ o $-1$ . Por lo tanto, las partículas elementales son fermions, cuyo factor de fase es $-1$ , o bosons, cuyo factor de fase es $1$ . Estos dos tipos tienen diferentes comportamientos estadísticos. Fermions obedecen las estadísticas de Fermi-Dirac, mientras que los bosons obedecen las estadísticas de Bose-Einstein. En particular, el factor de fase es por qué los fermions obedecen al principio de exclusión paúlí: Si dos fermions están en el mismo estado, entonces tenemos

{displaystyle left|psi psi rightrangle =-left|psi psi rightrangle.}

El vector de estado debe ser cero, lo que significa que no es normalizable y, por lo tanto, no es físico.

En sistemas bidimensionales, sin embargo, se pueden observar cuasipartículas que obedecen a estadísticas que oscilan continuamente entre las estadísticas de Fermi-Dirac y Bose-Einstein, como lo demostraron por primera vez Jon Magne Leinaas y Jan Myrheim de la Universidad de Oslo en 1977. en el caso de dos partículas esto se puede expresar como

{displaystyle left|psi _{1}psi _{2}rightrangle =e^{itheta }left|psi _{2}psi _{1}rightrangle}

Donde $e^{itheta }$ puede ser otros valores $-1$ o $1$ . Es importante señalar que hay un ligero abuso de notación en esta expresión corta, ya que en realidad esta función de onda puede ser y suele ser multivalorada. Esta expresión realmente significa que cuando la partícula 1 y la partícula 2 se intercambian en un proceso en el que cada uno de ellos hace una contrarrevolución a la mitad sobre el otro, el sistema de dos partículas vuelve a su función original de onda cuántica excepto multiplicado por el factor complejo de fase de unidad-normas eⁱ. Por el contrario, una media revolución de reloj resulta en multiplicar la función de onda por e⁻ⁱ. Tal teoría obviamente sólo tiene sentido en dos-dimensiones, donde el reloj y el sentido contrario son direcciones claramente definidas.

En el caso θ = π recuperamos las estadísticas de Fermi-Dirac (e^iπ = −1) y en el caso θ = 0 (o θ = 2π) las estadísticas de Bose-Einstein (e^2πi = 1). En el medio tenemos algo diferente. Frank Wilczek exploró en 1982 el comportamiento de tales cuasipartículas y acuñó el término "cualquiera" describirlos, porque pueden tener cualquier fase cuando se intercambian partículas. A diferencia de los bosones y fermiones, los cualquiera tienen la propiedad peculiar de que cuando se intercambian dos veces de la misma manera (por ejemplo, si cualquiera 1 y cualquiera 2 se hicieran girar en sentido contrario a las agujas del reloj media revolución entre sí para cambiar de lugar, y luego se giraran en sentido contrario a las agujas del reloj media revolución unos de otros para volver a sus lugares originales), la función de onda no es necesariamente la misma sino que generalmente se multiplica por alguna fase compleja (por e^2iθ en este ejemplo).

También podemos usar θ = 2π s con el número cuántico de espín de partículas s, siendo s un número entero para bosones, un medio entero para fermiones, de modo que

{displaystyle e^{itheta }=e^{2ipi s}=(-1)^{2s},}

{displaystyle left|psi _{1}psi _{2}rightrangle =(-1)^{2s}left|psi _{2}psi _{1}rightrangle.}

En un borde, los electrones cuánticos fraccionarios de efecto Hall están confinados a moverse en una dimensión espacial. Los modelos matemáticos de anyons unidimensionales proporcionan una base para las relaciones de conmutación que se muestran arriba.

En un espacio de posición tridimensional, los operadores estadísticos de fermiones y bosones (−1 y +1 respectivamente) son solo representaciones unidimensionales del grupo de permutaciones (S_N de N partículas indistinguibles) que actúan sobre el espacio de funciones de onda. De la misma manera, en un espacio de posición bidimensional, los operadores estadísticos abelianos anyónicos (e^iθ) son solo representaciones unidimensionales del grupo trenzado (B_N de N partículas indistinguibles) que actúan en el espacio de funciones de onda.. Las estadísticas anyónicas no abelianas son representaciones de dimensiones superiores del grupo de trenzas. Las estadísticas anyónicas no deben confundirse con las paraestadísticas, que describen estadísticas de partículas cuyas funciones de onda son representaciones de dimensiones superiores del grupo de permutación.

Equivalancia topológica

El hecho de que las clases de homotopía de caminos (es decir, la noción de equivalencia en trenzas) sean relevantes sugiere una idea más sutil. Surge de la integral de trayectoria de Feynman, en la que todos los caminos desde un punto inicial hasta un punto final en el espacio-tiempo contribuyen con un factor de fase apropiado. La integral de trayectoria de Feynman se puede motivar expandiendo el propagador utilizando un método llamado corte de tiempo, en el que el tiempo se discretiza.

En rutas no homotópicas, no se puede llegar desde ningún punto en un intervalo de tiempo a ningún otro punto en el siguiente intervalo de tiempo. Esto significa que podemos considerar que las clases de rutas de equivalencia homotópica tienen diferentes factores de ponderación.

Por lo tanto, se puede ver que la noción topológica de equivalencia proviene de un estudio de la integral de trayectoria de Feynman.

Did you mean:

For a more transparent way of seeing that the homotopic notion of equivalence is the "right " one to use, see Aharonov–Bohm effect.

Experimento

En 2020, dos equipos de científicos (uno en París y el otro en Purdue) anunciaron nuevas pruebas experimentales de la existencia de anyons. Ambos experimentos aparecieron en la publicación anual "estado de la ciencia" de 2020 de la revista Discover Magazine. asunto.

En abril de 2020, investigadores de la École normale supérieure (París) y el Centro de Nanociencias y Nanotecnologías (C2N) informaron sobre los resultados de un pequeño "colisionador de partículas" para cualquiera. Detectaron propiedades que coincidían con las predicciones de la teoría para cualquiera.

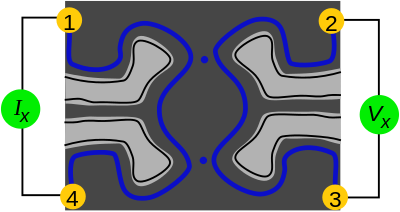
En julio de 2020, los científicos de la Universidad Purdue detectaron a cualquiera utilizando una configuración diferente. El interferómetro del equipo dirige los electrones a través de una nanoestructura grabada similar a un laberinto hecha de arseniuro de galio y arseniuro de galio y aluminio. "En el caso de nuestros anyons, la fase generada por el trenzado fue 2π/3," él dijo. "Eso es diferente de lo que se ha visto antes en la naturaleza".

Cualquier persona no abeliana

Problema no resuelto en la física:

¿Es estable el orden topológico a temperatura no cero?

(Problemas más no resueltos en física)

En 1988, Jürg Fröhlich demostró que, según el teorema de la estadística de espín, era válido que el intercambio de partículas fuera monoidal (estadística no abeliana). En particular, esto se puede lograr cuando el sistema exhibe cierta degeneración, de modo que múltiples estados distintos del sistema tengan la misma configuración de partículas. Entonces, un intercambio de partículas puede contribuir no sólo a un cambio de fase, sino que puede enviar el sistema a un estado diferente con la misma configuración de partículas. El intercambio de partículas corresponde entonces a una transformación lineal en este subespacio de estados degenerados. Cuando no hay degeneración, este subespacio es unidimensional y, por lo tanto, todas esas transformaciones lineales conmutan (porque son solo multiplicaciones por un factor de fase). Cuando hay degeneración y este subespacio tiene una dimensión más alta, entonces estas transformaciones lineales no necesitan conmutar (al igual que la multiplicación de matrices no lo hace).

Gregory Moore, Nicholas Read y Xiao-Gang Wen señalaron que las estadísticas no abelianas se pueden realizar en el efecto Hall cuántico fraccional (FQHE). Si bien al principio los anyons no abelianos generalmente se consideraban una curiosidad matemática, los físicos comenzaron a impulsar su descubrimiento cuando Alexei Kitaev demostró que los anyons no abelianos podían usarse para construir una computadora cuántica topológica. Hasta 2012, ningún experimento ha demostrado de manera concluyente la existencia de anyons no abelianos, aunque están surgiendo pistas prometedoras en el estudio del estado ν = 5/2 FQHE. En octubre de 2013 se presentó evidencia experimental de anones no abelianos, aunque aún no es concluyente y actualmente es cuestionada. Trabajos recientes afirman la creación de un orden topológico no abeliano y anyons en un procesador de iones atrapados y la demostración del trenzado no abeliano de vértices de gráficos en un procesador superconductor.

Fusión de cualquiera

De la misma manera que dos fermiones (por ejemplo, ambos de espín 1/2) pueden considerarse juntos como un bosón compuesto (con espín total en una superposición de 0 y 1), dos o más cualquieras juntos forman un anyon compuesto (posiblemente un bosón o fermión). Se dice que el anyon compuesto es el resultado de la fusión de sus componentes.

Si $N$ idéntico abeliano cada uno con estadísticas individuales $alpha$ (es decir, el sistema recoge una fase ${displaystyle e^{ialpha }}$ cuando dos individuos se someten a un intercambio adiabático de contramano) todos los fusibles juntos, tienen estadísticas ${displaystyle N^{2}alpha }$ . Esto se puede ver notando que en la rotación de dos elementos compuestos sobre uno al otro, hay $N^{2}$ pares de matones individuales (uno en el primer composite cualquiera, uno en el segundo composite cualquiera) que cada contribuyen una fase ${displaystyle e^{ialpha }}$ . Un análisis análogo se aplica a la fusión de los abelios no identicos. Las estadísticas del conjunto se determinan de forma única por las estadísticas de sus componentes.

Los anyons no abelianos tienen relaciones de fusión más complicadas. Como regla general, en un sistema con aniones no abelianos, hay una partícula compuesta cuya etiqueta estadística no está determinada únicamente por las etiquetas estadísticas de sus componentes, sino que existe como una superposición cuántica (esto es completamente análogo a cómo dos fermiones conocidos tener espín 1/2 están juntos en superposición cuántica del espín total 1 y 0). Si se conocen las estadísticas generales de la fusión de varios anyons, todavía hay ambigüedad en la fusión de algunos subconjuntos de esos anyons, y cada posibilidad es un estado cuántico único. Estos múltiples estados proporcionan un espacio de Hilbert en el que se pueden realizar cálculos cuánticos.

Base topológica

Rotación anticipada

Rotación del reloj

Intercambio de dos partículas en 2 + 1 espacio por rotación. Las rotaciones son inequivalentes, ya que no se puede deformar en la otra (sin las mundanas que salen del avión, una imposibilidad en el espacio 2d).

En más de dos dimensiones, el teorema de la estadística de espín establece que cualquier estado multipartícula de partículas indistinguibles tiene que obedecer a las estadísticas de Bose-Einstein o Fermi-Dirac. Para cualquier d > 2, los grupos de Lie SO(d,1) (que generaliza el grupo de Lorentz) y Poincaré(d,1) tienen Z₂ como su primer grupo de homotopía. Debido a que el grupo cíclico Z₂ está compuesto de dos elementos, sólo quedan dos posibilidades. (Los detalles son más complicados que eso, pero éste es el punto crucial).

La situación cambia en dos dimensiones. Aquí el primer grupo de homotopía de SO(2,1), y también de Poincaré(2,1), es Z (cíclico infinito). Esto significa que Spin(2,1) no es la cobertura universal: no está simplemente conexo. En detalle, existen representaciones proyectivas del grupo ortogonal especial SO(2,1) que no surgen de representaciones lineales de SO(2,1), o de su doble cobertura, el grupo de espín Spin(2,1). Los anyons son representaciones uniformemente complementarias de la polarización del espín de una partícula cargada.

Este concepto también se aplica a sistemas no relativistas. La parte relevante aquí es que el grupo de rotación espacial SO (2) tiene un primer grupo de homotopía infinito.

Este hecho también está relacionado con los grupos de trenzas bien conocidos en la teoría de nudos. La relación se puede entender cuando se considera el hecho de que en dos dimensiones el grupo de permutaciones de dos partículas ya no es el grupo simétrico S₂ (con dos elementos) sino más bien el grupo trenzado B₂ (con un número infinito de elementos). Lo esencial es que una trenza se puede enrollar alrededor de la otra, operación que se puede realizar infinitas veces, tanto en el sentido de las agujas del reloj como en el sentido contrario.

Un enfoque muy diferente al problema de estabilidad-decoherencia en la computación cuántica es crear una computadora cuántica topológica con anyons, cuasipartículas utilizadas como hilos y basándose en la teoría de la trenza para formar puertas lógicas cuánticas estables.

Generalización a dimensiones superiores

Las excitaciones fraccionadas como partículas puntuales pueden ser bosones, fermiones o cualquiera en dimensiones espacio-temporales 2+1. Se sabe que las partículas puntuales sólo pueden ser bosones o fermiones en dimensiones espacio-temporales 3+1 y superiores. Sin embargo, las excitaciones en forma de bucle (o cuerda) o membrana son objetos extendidos que pueden tener estadísticas fraccionadas. La investigación actual muestra que las excitaciones en forma de bucles y cuerdas existen para órdenes topológicos en el espacio-tiempo de 3+1 dimensiones, y sus estadísticas de múltiples bucles/trenzado de cuerdas son las firmas clave para identificar órdenes topológicos de 3+1 dimensiones. Las estadísticas de bucles múltiples/trenzado de cuerdas de órdenes topológicos de 3+1 dimensiones pueden capturarse mediante los invariantes de enlace de teorías de campos cuánticos topológicos particulares en 4 dimensiones de espacio-tiempo. Explicado de manera coloquial, los objetos extendidos (bucle, cuerda o membrana, etc.) pueden ser potencialmente cualquierónicos en dimensiones espacio-temporales 3+1 y superiores en los sistemas entrelazados de largo alcance.

Más resultados...