Cuadrilátero cíclico

Ejemplos de cuadriláteros cíclicos

En geometría euclidiana, un cuadrilátero cíclico o cuadrilátero inscrito es un cuadrilátero cuyos vértices se encuentran todos en un solo círculo. Este círculo se llama circumcircle o círculo circunscrito, y se dice que los vértices son concíclicos. El centro del círculo y su radio se denominan circuncentro y circunradio respectivamente. Otros nombres para estos cuadriláteros son cuadrilátero concíclico y cuadrilátero cordal, este último ya que los lados del cuadrilátero son cuerdas del circuncírculo. Por lo general, se supone que el cuadrilátero es convexo, pero también hay cuadriláteros cíclicos cruzados. Las fórmulas y propiedades dadas a continuación son válidas en el caso convexo.

La palabra cíclico proviene del griego antiguo κύκλος (kuklos), que significa "círculo" o "rueda".

Todos los triángulos tienen un círculo circunscrito, pero no todos los cuadriláteros. Un ejemplo de un cuadrilátero que no puede ser cíclico es un rombo no cuadrado. Las caracterizaciones de la sección a continuación establecen qué condiciones necesarias y suficientes debe cumplir un cuadrilátero para tener un circuncírculo.

Casos especiales

Todo cuadrado, rectángulo, trapezoide isósceles o antiparalelogramo es cíclico. Una cometa es cíclica si y solo si tiene dos ángulos rectos: una cometa recta. Un cuadrilátero bicéntrico es un cuadrilátero cíclico que también es tangencial y un cuadrilátero ex-bicéntrico es un cuadrilátero cíclico que también es ex-tangencial. Un cuadrilátero armónico es un cuadrilátero cíclico en el que el producto de las longitudes de los lados opuestos es igual.

Caracterizaciones

ABCD cuadrilátero cíclico

Circuncentro

Un cuadrilátero convexo es cíclico si y solo si las cuatro bisectrices perpendiculares a los lados son concurrentes. Este punto común es el circuncentro.

Ángulos suplementarios

Un cuadrilátero convexo ABCD es cíclico si y solo si sus ángulos opuestos son suplementarios, es decir

α α +γ γ =β β +δ δ =π π rad()=180∘ ∘ ).{displaystyle alpha +gamma =beta +delta =pi {text{rad} (=180^{circ }}

El teorema directo fue la Proposición 22 en el Libro 3 de los Elementos de Euclides. De manera equivalente, un cuadrilátero convexo es cíclico si y solo si cada ángulo exterior es igual al ángulo interior opuesto.

En 1836 Duncan Gregory generalizó este resultado como sigue: Dado cualquier cíclico convexo 2n-gon, entonces las dos sumas de suplente los ángulos interiores son iguales a (n-1)π π {displaystyle pi}.

Tomando la proyección estereográfica (tangente de medio ángulo) de cada ángulo, esto se puede reexpresar,

#⁡ ⁡ α α 2+#⁡ ⁡ γ γ 21− − #⁡ ⁡ α α 2#⁡ ⁡ γ γ 2=#⁡ ⁡ β β 2+#⁡ ⁡ δ δ 21− − #⁡ ⁡ β β 2#⁡ ⁡ δ δ 2=JUEGO JUEGO .{fnMicroc {fnMicroc} {fnMicroc} {gnMicroc {gnMicrosoft}cH} {fnK} {fn}} {fnK} {fn}}tan {fn}fn} {fn} {fn0}}}}}} {fnfnfnfnfn}}}} {fnfnfnfnfnfn9fnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfn}fnfn}fnfn}fnfn}fnfnfnfnfnfnfnfn}fnfnfnfnfnfnfn}fnfn {gamma} {fnMicroc {fnMicroc {beta ## {2}+tan {frac {delta {fn} {fn} {fnK}}tan {fnfn}}tan {fn}fn} {fn}fn}fn}fn} {fn}fnfn}} {fnfnfnfn9fnfnfnfnfnfnfnfnfnfnfnfnfn9}fn9}fnfn}fnfnfnfnfn}fnfnfnfn}fnfn}fnfnfnfnfnfnfnfn}fnfnfnfnfnfnfnfn}fnfn}fnfnfnfn}fnfn}fn}fn - ¿Qué?

Lo que implica que

#⁡ ⁡ α α 2#⁡ ⁡ γ γ 2=#⁡ ⁡ β β 2#⁡ ⁡ δ δ 2=1{displaystyle tan {frac {fn} {fn}tan {fnMic {gn0}}=tan {beta} # {2}{tan {frac {delta } {2}=1}

Ángulos entre lados y diagonales

Un cuadrilátero convexo ABCD es cíclico si y solo si el ángulo entre un lado y una diagonal es igual al ángulo entre el lado opuesto y la otra diagonal. Es decir, por ejemplo,

∠ ∠ ACB=∠ ∠ ADB.{displaystyle angle ACB=angle ADB.}

Puntos Pascales

ABCD es un cuadrilátero cíclico. E es el punto de intersección de las diagonales y F es el punto de intersección de las extensiones de los lados BC y AD. ⋅ ⋅ {displaystyle omega } es un círculo cuyo diámetro es el segmento, EF. P y Q son puntos pascales formados por el círculo ⋅ ⋅ {displaystyle omega }. Triángulos FAB y FCD son similares.

Otra condición necesaria y suficiente para un cuadrilátero convexo ABCD ser cíclico son: E ser el punto de intersección de las diagonales, dejar F ser el punto de intersección de las extensiones de los lados AD y BC, vamos ⋅ ⋅ {displaystyle omega } ser un círculo cuyo diámetro es el segmento, EF, y dejar P y Q ser puntos de Pascal en los lados AB y CD formado por el círculo ⋅ ⋅ {displaystyle omega }.
1) ABCD es un cuadrilátero cíclico si y sólo si puntos P y Q son collinear con el centro O, de círculo ⋅ ⋅ {displaystyle omega }.
2) ABCD es un cuadrilátero cíclico si y sólo si puntos P y Q son los puntos intermedios de los lados AB y CD.

Intersección de diagonales

Si hay dos líneas, una que contiene el segmento AC y la otra que contiene el segmento BD, intersección en E, luego los cuatro puntos A, B, C, D son concíclicos si y solo si

AE⋅ ⋅ EC=BE⋅ ⋅ ED.{displaystyle displaystyle AEcdot EC=BEcdot ED.}

La intersección E puede ser interna o externa al círculo. En el primer caso, el cuadrilátero cíclico es ABCD, y en el último caso, el cuadrilátero cíclico es ABDC. Cuando la intersección es interna, la igualdad establece que el producto de las longitudes de los segmentos en que E divide una diagonal es igual a la de la otra diagonal. Esto se conoce como el teorema de las cuerdas que se cortan ya que las diagonales del cuadrilátero cíclico son cuerdas del circuncírculo.

Teorema de Ptolomeo

El teorema de Ptolomeo expresa el producto de las longitudes de las dos diagonales e y f de un cuadrilátero cíclico igual a la suma de los productos de los lados opuestos:

ef=ac+bd,{displaystyle displaystyle ef=ac+bd,}

donde a, b, c, d son las longitudes de los lados en orden. Lo contrario también es cierto. Es decir, si esta ecuación se cumple en un cuadrilátero convexo, entonces se forma un cuadrilátero cíclico.

Triángulo diagonal

ABCD es un cuadrilátero cíclico. EFG es el triángulo diagonal de ABCD. El punto T de intersección de los bimedianos de ABCD pertenece al círculo de nueve puntos EFG.

En un cuadrilátero convexo ABCD, vamos EFG ser el triángulo diagonal de ABCD y dejar ⋅ ⋅ {displaystyle omega } ser el círculo de nueve puntos EFG. ABCD es cíclico si y sólo si el punto de intersección de los bimedianos de ABCD pertenece al círculo de nueve puntos ⋅ ⋅ {displaystyle omega }.

Área

El área K de un cuadrilátero cíclico con lados a, b, c, d está dada por la fórmula de Brahmagupta

K=()s− − a)()s− − b)()s− − c)()s− − d){displaystyle K={sqrt {(s-a)(s-b)(s-c)},}

donde s, el semiperímetro, es s = 1/2(a + b + c + d). Este es un corolario de la fórmula de Bretschneider para el cuadrilátero general, ya que los ángulos opuestos son suplementarios en el caso cíclico. Si también d = 0, el cuadrilátero cíclico se convierte en un triángulo y la fórmula se reduce a la fórmula de Heron.

El cuadrilátero cíclico tiene un área máxima entre todos los cuadriláteros que tienen los mismos lados (independientemente de la secuencia). Este es otro corolario de la fórmula de Bretschneider. También se puede demostrar mediante cálculo.

Cuatro longitudes desiguales, cada una menor que la suma de las otras tres, son los lados de cada uno de los tres cuadriláteros cíclicos no congruentes, que según la fórmula de Brahmagupta tienen la misma área. Específicamente, para los lados a, b, c, y d, lado a podría ser opuesto a cualquiera de los lados b, lado c , o lado d.

El área de un cuadrilátero cíclico con lados sucesivos a, b, c, d, ángulo A entre los lados a y d, y el ángulo B entre los lados a y b se pueden expresar como

K=12()ab+cd)pecado⁡ ⁡ B{displaystyle K={tfrac {1}{2}(ab+cd)sin {B}

o

K=12()ad+bc)pecado⁡ ⁡ A{displaystyle K={tfrac {2} {bc}sin {A}}

o

K=12()ac+bd)pecado⁡ ⁡ Silencio Silencio {displaystyle K={tfrac {2} {c+bd)sin {thetat }

donde θ es cualquier ángulo entre las diagonales. Siempre que A no sea un ángulo recto, el área también se puede expresar como

K=14()a2− − b2− − c2+d2)#⁡ ⁡ A.{displaystyle K={tfrac {1} {4}(a^{2}-b^{2}-c^{2}+d^{2})tan {A}

Otra fórmula es

K=2R2pecado⁡ ⁡ Apecado⁡ ⁡ Bpecado⁡ ⁡ Silencio Silencio {displaystyle displaystyle K=2R^{2}sin {B}sin {theta}}

donde R es el radio del círculo circunscrito. Como consecuencia directa,

K≤ ≤ 2R2{displaystyle Kleq 2R^{2}

donde hay igualdad si y solo si el cuadrilátero es un cuadrado.

Diagonales

En un cuadrilátero cíclico con vértices sucesivos A, B, C, D y lados a = AB, b = BC , c = CD y d = DA, las longitudes de las diagonales p = AC y q = BD se puede expresar en términos de los lados como

p=()ac+bd)()ad+bc)ab+cd{displaystyle p={sqrt {frac {(ac+bd)}{ab+cd}}}} y q=()ac+bd)()ab+cd)ad+bc{displaystyle q={sqrt {frac {(ac+bd)}{ad+bc}}}}

así que muestra el teorema de Ptolomeo

pq=ac+bd.{displaystyle pq=ac+bd.}

Según el segundo teorema de Ptolomeo

pq=ad+bcab+cd{fnMicroc} {fnK}={f} {ad+bc}{ab+cd}}

usando las mismas notaciones que arriba.

Para la suma de las diagonales tenemos la desigualdad

p+q≥ ≥ 2ac+bd.{displaystyle p+qgeq 2{sqrt {ac+bd}}.

La igualdad se cumple si y solo si las diagonales tienen la misma longitud, lo que se puede probar usando la desigualdad AM-GM.

Además,

()p+q)2≤ ≤ ()a+c)2+()b+d)2.{displaystyle (p+q)^{2}leq (a+c)^{2}+(b+d)^{2}

En cualquier cuadrilátero convexo, las dos diagonales juntas dividen el cuadrilátero en cuatro triángulos; en un cuadrilátero cíclico, los pares opuestos de estos cuatro triángulos son similares entre sí.

Si M y N son los puntos medios de la diagonales AC y BD, entonces

MNEF=12SilencioACBD− − BDACSilencio{displaystyle {frac {fn}={frac {1}{2}left forever{frac} {f}f} {fnK}}f}}fnK} Está bien.

donde E y F son los puntos de intersección de las extensiones de los lados opuestos.

Si ABCD es un cuadrilátero cíclico donde AC se encuentra BD en E, luego

AECE=ABCB⋅ ⋅ ADCD.{displaystyle {frac {fnMicroc}cdot {fnMicroc {}}}} {fnMicroc {fnMicroc}}}

Un conjunto de lados que pueden formar un cuadrilátero cíclico se puede organizar en cualquiera de tres secuencias distintas, cada una de las cuales puede formar un cuadrilátero cíclico de la misma área en el mismo círculo (las áreas son las mismas según Brahmagupta' fórmula del área s). Dos cualesquiera de estos cuadriláteros cíclicos tienen una longitud diagonal en común.

Fórmulas de ángulos

Para un cuadrilátero cíclico con lados sucesivos a, b, c, d, semiperímetro s, y el ángulo A entre los lados a y d, las funciones trigonométricas de A están dadas por

#⁡ ⁡ A=a2− − b2− − c2+d22()ad+bc),{displaystyle cos A={frac {a^{2}-b^{2}-c^{2}+d^{2}{2(ad+bc)}}}}

pecado⁡ ⁡ A=2()s− − a)()s− − b)()s− − c)()s− − d)()ad+bc),{displaystyle sin A={frac {2{sqrt {(s-a)(s-b)(s-c)}}{(ad+bc)}}}}

#⁡ ⁡ A2=()s− − a)()s− − d)()s− − b)()s− − c).{displaystyle tan {frac {A}{2}={sqrt {frac {(s-a)}{(s-b)(s-c)}}}}}}

El ángulo θ entre las diagonales de los lados opuestos a y c satisface

#⁡ ⁡ Silencio Silencio 2=()s− − b)()s− − d)()s− − a)()s− − c).{displaystyle tan {fractheta {fnK} {fnMicroc { s-b)}{(s-a)(s-c)}}}}}

Si las extensiones de los lados opuestos a y c se cruzan en un ángulo φ, entonces

#⁡ ⁡ φ φ 2=()s− − b)()s− − d)()b+d)2()ab+cd)()ad+bc){displaystyle cos {frac {fnh00\fnh00\\fnMicrosoft {\fn\\\\\\\\\\\\\\\\\fnMicrosoft {\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ # {2}={sqrt {frac {(s-b)(s-d)(b+d)^{2}{(ab+cd)(ad+bc)}}}}

donde s es el semiperímetro.

Fórmula del circunradio de Parameshvara

Un cuadrilátero cíclico con lados sucesivos a, b, c, d y semiperímetro s tiene el circunradio (el radio del círculo) dado por

R=14()ab+cd)()ac+bd)()ad+bc)()s− − a)()s− − b)()s− − c)()s− − d).{displaystyle R={frac {1}{4}{sqrt {frac {(ab+cd)(ac+bd)(ad+bc)}{(s-a)(s-b)(s-c)(s-d)}}}}}{(s-a)

Esto fue derivado por el matemático indio Vatasseri Parameshvara en el siglo XV.

Usando la fórmula de Brahmagupta, la fórmula de Parameshvara se puede reformular como

4KR=()ab+cd)()ac+bd)()ad+bc){displaystyle 4KR={sqrt {(ab+cd)(ac+bd)(ad+bc)}}}

donde K es el área del cuadrilátero cíclico.

Anticentro y colinealidades

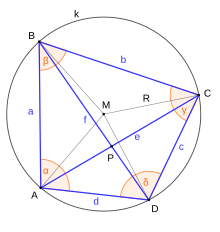
Cuatro segmentos de línea, cada uno perpendicular a un lado de un cuadrilátero cíclico y que pasa por el punto medio del lado opuesto, son concurrentes. Estos segmentos de línea se denominan maltitudes, que es una abreviatura de punto medio de altitud. Su punto común se llama anticentro. Tiene la propiedad de ser el reflejo del circuncentro en el "centroide del vértice". Por lo tanto, en un cuadrilátero cíclico, el circuncentro, el "centroide del vértice" y el anticentro son colineales.

Si las diagonales de un cuadrilátero cíclico se cortan en P, y los puntos medios de las diagonales son M y N, entonces el anticentro del cuadrilátero es el ortocentro del triángulo MNP.

El anticentro de un cuadrilátero cíclico es el punto de Poncelet de sus vértices.

Otras propiedades

Teorema japonesa

• En un cuadrilátero cíclico ABCD, los incentros M₁, M₂, M₃, M₄ (ver la figura a la derecha) en triángulos DAB, ABC, BCD, y CDA son los vértices de un rectángulo. Este es uno de los teoremas conocidos como el teorema japonés. Los ortocentros de los mismos cuatro triángulos son los vértices de un congruente cuadrilátero a ABCD, y los centroides en esos cuatro triángulos son vertices de otro cuadrilátero cíclico.
• En un cuadrilátero cíclico ABCD con circuncentro O, vamos P ser el punto donde las diagonales AC y BD Intersecta. Entonces ángulo APB es la media aritmética de los ángulos AOB y COD. Esta es una consecuencia directa del teorema de ángulo inscrito y el teorema de ángulo exterior.
• No hay cuadriláteros cíclicos con área racional y con lados racionales desiguales en progresión aritmética o geométrica.

• Si un cuadrilátero cíclico tiene longitudes laterales que forman una progresión aritmética, el cuadrilátero también es ex-bicentrico.
• Si los lados opuestos de un cuadrilátero cíclico se extienden para reunirse en E y F, entonces los bisectores de ángulo interno de los ángulos en E y F son perpendiculares.

Cuadriláteros de Brahmagupta

Un cuadrilátero Brahmagupta es un cuadrilátero cíclico con lados enteros, diagonales enteras y área entera. Todos los cuadriláteros de Brahmagupta con lados a, b, c, d, diagonales e, f, área K, y circunradius R se pueden obtener borrando los denominadores de las siguientes expresiones que involucran parámetros racionales t, u y v:

a=[t()u+v)+()1− − uv)][u+v− − t()1− − uv)]{displaystyle a=[t(u+v)+(1-uv)] [u+v-t(1-uv)]}

b=()1+u2)()v− − t)()1+tv){displaystyle b=(1+u^{2})(v-t)(1+tv)}

c=t()1+u2)()1+v2){displaystyle c=t(1+u^{2})(1+v^{2}}

d=()1+v2)()u− − t)()1+tu){displaystyle d=(1+v^{2})(u-t)(1+tu)}

e=u()1+t2)()1+v2){displaystyle e=u(1+t^{2})(1+v^{2}}

f=v()1+t2)()1+u2){displaystyle f=v(1+t^{2})(1+u^{2}}

K=uv[2t()1− − uv)− − ()u+v)()1− − t2)][2()u+v)t+()1− − uv)()1− − t2)]{displaystyle K=uv[2t(1-uv)-(u+v)(1-t^{2}) [2(u+v)t+(1-uv)(1-t^{2}]

4R=()1+u2)()1+v2)()1+t2).{displaystyle 4R=(1+u^{2})(1+v^{2})(1+t^{2}). }

Caso ortodiagonal

Circunradio y área

Para un cuadrilátero cíclico que también es ortodiagonal (tiene diagonales perpendiculares), suponga que la intersección de las diagonales divide una diagonal en segmentos de longitud p₁ y p₂ y divide la otra diagonal en segmentos de longitud q₁ y q₂. Entonces (la primera igualdad es la Proposición 11 en el Libro de Lemas de Arquímedes)

D2=p12+p22+q12+q22=a2+c2=b2+d2{displaystyle ¿Qué?

donde D es el diámetro del círculo circunscrito. Esto se cumple porque las diagonales son cuerdas perpendiculares de un círculo. Estas ecuaciones implican que el circunradio R se puede expresar como

R=12p12+p22+q12+q22{displaystyle R={tfrac {1}{2}{sqrt {fn} {2} {2}}}} {2}}}}*

o, en términos de los lados del cuadrilátero, como

R=12a2+c2=12b2+d2.{displaystyle R={tfrac {2}{2} {sqrt {2}}={tfrac}}={tfrac} {1}{2} {sqrt {b^{2}}}} {2}} {cH00}} {cH00}} {ccH00}}} {cH00}} {cH00}}} {cH00}}} {cH00}} {ccH00}}}} {ccH00}}}}}}}}}}} {ccccccH00}}}}}}}} {cH00}}}}}} {ccccccH00}}}}}}}} {cccccccccccccccccccccccccccH00}} {cH00}}}}}}}}}}}}}}}}}}}}}}} {cc

También se sigue que

a2+b2+c2+d2=8R2.{displaystyle a^{2}+b^{2}+c^{2}+d^{2}=8R^{2}

Por lo tanto, según el teorema del cuadrilátero de Euler, el circunradio se puede expresar en términos de las diagonales p y q, y la distancia x entre los puntos medios de las diagonales como

R=p2+q2+4x28.{displaystyle R={sqrt {frac {p^{2}+q^{2}+4x^{2}}}}}

Una fórmula para el área K de un cuadrilátero ortodiagonal cíclico en términos de los cuatro lados se obtiene directamente al combinar el teorema de Ptolomeo y la fórmula para el área de un cuadrilátero ortodiagonal. El resultado es

K=12()ac+bd).{displaystyle K={tfrac {2}(ac+bd).}

Otras propiedades

• En un cuadrilátero ortodiagonal cíclico, el anticentro coincide con el punto en que las diagonales se intersectan.
• El teorema de Brahmagupta afirma que para un cuadrilátero cíclico que también es ortodiagonal, el perpendicular de cualquier lado a través del punto de intersección de las diagonales bisectos del lado opuesto.
• Si un cuadrilátero cíclico es también ortodiagonal, la distancia del circuncentro a cualquier lado equivale a la mitad de la longitud del lado opuesto.
• En un cuadrilátero ortodiagonal cíclico, la distancia entre los puntos intermedios de las diagonales equivale a la distancia entre el circuncentro y el punto donde las diagonales se intersectan.

Cuadriláteros esféricos cíclicos

En geometría esférica, un cuadrilátero esférico formado por cuatro círculos mayores que se cruzan es cíclico si y solo si las sumas de los ángulos opuestos son iguales, es decir, α + γ = β + δ para ángulos consecutivos α, β, γ, δ del cuadrilátero. I. A. Lexell demostró una dirección de este teorema en 1786. Lexell demostró que en un cuadrilátero esférico inscrito en un círculo pequeño de una esfera, las sumas de los ángulos opuestos son iguales, y que en el cuadrilátero circunscrito, las sumas de los lados opuestos son iguales. El primero de estos teoremas es el análogo esférico de un teorema del plano, y el segundo teorema es su dual, es decir, el resultado de intercambiar círculos máximos y sus polos. Kiper et al. demostró un inverso del teorema: si las sumas de los lados opuestos son iguales en un cuadrilátero esférico, entonces existe un círculo de inscripción para este cuadrilátero.