Cuádrica
En matemáticas, una superficie quadric de quadric o quadric ( Hyperfuerza de hiperebra quadric en dimensiones superiores), es una generalización de secciones cónicas (elipses, parabolas, parabolas e Hyperbolas). Es una hiperrajes (de dimensión d ) en un ( d + 1) --dimensional espacio, y se define como el conjunto cero de un polinomio irreducible de grado dos en las variables d + 1; Por ejemplo, d = 1 en el caso de las secciones cónicas. Cuando el polinomio de definición no es absolutamente irreducible, el conjunto cero generalmente no se considera un quadric, aunque a menudo se llama un quadric de degenerado o un quadric reducible .
en coordenadas x 1 , x 2 ,..., x d +1 , el quadric general se define por la ecuación algebraica
- .. i,j=1D+1xiQijxj+.. i=1D+1Pixi+R=0{displaystyle sum _{i,j=1}{D+1}x_{i}Q_{ij}x_{j}+sum ¿Por qué?
que puede escribirse de forma compacta en notación vectorial y matricial como:
- xQxT+PxT+R=0{displaystyle xQx^{mathrm ¿Qué?
where x = ( x 1 , x 2 ,..., x d +1 ) es un vector de fila, x t es la transposición de x (un vector de columna), q es a ( D + 1) × ( d + 1) matriz y p es un ( D + 1) --Dimensional Row Vector y r una constante escalar. Los valores Q , p y r a menudo se consideran sobre números reales o números complejos, pero se puede definir un quadric en cualquier campo.
Un quadric es una variedad algebraica afín o, si es reducible, un conjunto algebraico afín. Los cuadrados también se pueden definir en espacios proyectivos; Ver § Forma normal de cuadrados proyectivos, a continuación.
plano euclidiano
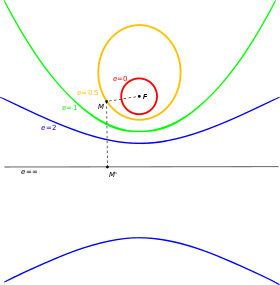
Como la dimensión de un plano euclidiano es dos, los cuadrados en un plano euclidiano tienen una dimensión una y, por lo tanto, son curvas de plano. Se llaman secciones cónicas , o cónicas .
Espacio euclidiano
En el espacio euclidiano tridimensional, las cuádricas tienen dimensión dos y se conocen como superficies cuádricas. Sus ecuaciones cuadráticas tienen la forma
- Ax2+BSí.2+Cz2+DxSí.+ESí.z+Fxz+Gx+HSí.+Iz+J=0,{displaystyle Ax^{2}+By^{2}+Cz^{2}+Dxy+Eyz+Fx+Gx+Hy+Iz+J=0,}
Donde A,B,...... ,J{displaystyle A,B,ldotsJ} son números reales, y al menos uno de A, B, y C No es cero.
Las superficies cuádricas se clasifican y nombran por su forma, que corresponde a las órbitas bajo transformaciones afines. Es decir, si una transformación afín asigna una cuádrica a otra, pertenecen a la misma clase y comparten el mismo nombre y muchas propiedades.
El teorema del eje principal muestra que para cualquier cuádrica (posiblemente reducible), un cambio adecuado de coordenadas cartesianas o, de manera equivalente, una transformación euclidiana permite poner la ecuación de la cuádrica en una única forma simple en la que la clase de la cuádrica es inmediatamente visible. Esta forma se llama la forma normal de la ecuación, ya que dos cuádricas tienen la misma forma normal si y solo si hay una transformación euclidiana que relaciona una cuádrica con la otra. Las formas normales son las siguientes:
- x2a2+Sí.2b2+ε ε 1z2c2+ε ε 2=0,{displaystyle {x^{2} over a^{2}+{y^{2} over b^{2}}+varepsilon _{1}{2}over c^{2}}+varepsilon _{2}=0,}
- x2a2− − Sí.2b2+ε ε 3=0{displaystyle {x^{2}varepsilon} ¿Qué?
- x2a2+ε ε 4=0,{displaystyle {x^{2}varepsilon ¿Qué?
- z=x2a2+ε ε 5Sí.2b2,{displaystyle z={x^{2}varepsilon _{5}{2} over b^{2}}}
Donde ε ε i{displaystyle varepsilon _{i} son 1, –1 o 0, excepto ε ε 3{displaystyle varepsilon ¿Qué? que toma sólo el valor 0 o 1.
Cada una de estas 17 formas normales corresponde a una sola órbita bajo transformaciones de afina. En tres casos no hay puntos reales: ε ε 1=ε ε 2=1{displaystyle varepsilon _{1}=varepsilon ¿Qué? ()imaginario ellipsoide), ε ε 1=0,ε ε 2=1{displaystyle varepsilon _{1}=0,varepsilon ¿Qué? ()cilindro elíptico imaginario), y ε ε 4=1{displaystyle varepsilon ¿Qué? (pair de planos complejos conjugados paralelos, un quadric reducible). En un caso, el imaginario cono, hay un solo punto (ε ε 1=1,ε ε 2=0{displaystyle varepsilon _{1}=1,varepsilon ¿Qué?). Si ε ε 1=ε ε 2=0,{displaystyle varepsilon _{1}=varepsilon ¿Qué? uno tiene una línea (de hecho dos planos complejos conjugados intersecting). Para ε ε 3=0,{displaystyle varepsilon _{3}=0,} uno tiene dos aviones de intersección (cantible quadric). Para ε ε 4=0,{displaystyle varepsilon _{4}=0,} uno tiene un avión doble. Para ε ε 4=− − 1,{displaystyle varepsilon - ¿Qué? uno tiene dos planos paralelos (cuádrico reducible).
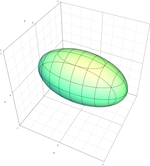
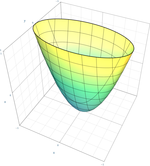
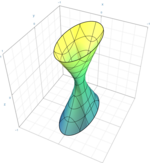
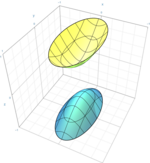
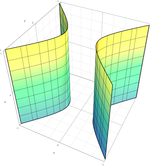
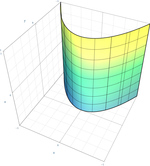
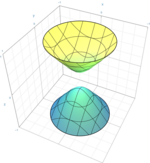
Así, entre las 17 formas normales, hay nueve cuádricas verdaderas: un cono, tres cilindros (a menudo llamadas cuádricas degeneradas) y cinco cuádricas no degeneradas (elipsoide, paraboloides e hiperboloides), que se detallan en las siguientes tablas. Las ocho cuádricas restantes son el elipsoide imaginario (sin punto real), el cilindro imaginario (sin punto real), el cono imaginario (un solo punto real) y las cuádricas reducibles, que se descomponen en dos planos; hay cinco cuádricas descompuestas, dependiendo de si los planos son distintos o no, paralelos o no, reales o complejos conjugados.
Cuando dos o más de los parámetros de la ecuación canónica son iguales, se obtiene una cuádrica de revolución, que permanece invariante cuando se gira alrededor de un eje (o infinitos ejes, en el caso de la esfera).
Definición y propiedades básicas
Una cuádrica afín es el conjunto de ceros de un polinomio de grado dos. Cuando no se especifica lo contrario, se supone que el polinomio tiene coeficientes reales y los ceros son puntos en un espacio euclidiano. Sin embargo, la mayoría de las propiedades siguen siendo verdaderas cuando los coeficientes pertenecen a cualquier campo y los puntos pertenecen a un espacio afín. Como suele ocurrir en la geometría algebraica, suele ser útil considerar puntos sobre un campo algebraicamente cerrado que contiene los coeficientes polinómicos, generalmente los números complejos, cuando los coeficientes son reales.
Muchas propiedades se vuelven más fáciles de enunciar (y demostrar) al extender la cuádrica al espacio proyectivo mediante la terminación proyectiva, que consiste en sumar puntos en el infinito. Técnicamente, si
- p()x1,...... ,xn){displaystyle p(x_{1},ldotsx_{n}}
es un polinomio de grado dos que define una cuádrica afín, entonces su terminación proyectiva se define homogeneizando p en
- P()X0,...... ,Xn)=X02p()X1X0,...... ,XnX0){displaystyle P(X_{0},ldotsX_{n}=X_{0}^{2},pleft({frac {X_{1} {X_{0}}}ldots{frac {X_{n} {X_{0}}derecha)}
(este es un polinomio, porque el grado de p es dos). Los puntos de terminación proyectiva son los puntos del espacio proyectivo cuyas coordenadas proyectivas son ceros de P.
Entonces, una cuádrica proyectiva es el conjunto de ceros en un espacio proyectivo de un polinomio homogéneo de grado dos.
Como el proceso anterior de homogeneización se puede revertir configurando X0 = 1:
- p()x1,...... ,xn)=P()1,x1,...... ,xn),{displaystyle p(x_{1},ldotsx_{n}=P(1,x_{1},ldotsx_{n}),}
a menudo es útil no distinguir un afine quadric de su terminación proyectiva, y hablar de la affine ecuación o el ecuación proyectiva de un quadric. Sin embargo, esto no es una equivalencia perfecta; es generalmente el caso de que P()X)=0{displaystyle P(mathbf {X}=0} incluirá puntos con X0=0{displaystyle X_{0}=0}, que no son también soluciones de p()x)=0{displaystyle p(mathbf {x}=0} porque estos puntos en el espacio proyector corresponden a puntos "en infinito" en el espacio afinado.
Ecuación
Una cuádrica en un espacio afín de dimensión n es el conjunto de ceros de un polinomio de grado 2. Es decir, es el conjunto de los puntos cuyas coordenadas satisfacen una ecuación
- p()x1,...... ,xn)=0,{displaystyle p(x_{1},ldotsx_{n}=0,}
donde el polinomio p tiene la forma
- p()x1,...... ,xn)=.. i=1n.. j=1nai,jxixj+.. i=1n()ai,0+a0,i)xi+a0,0,{displaystyle p(x_{1},ldotsx_{n}=sum - ¿Qué? ##{j=1} {n}a_{i,j}x_{i}x_{j}+sum ¿Qué?
para una matriz A=()ai,j){displaystyle A=(a_{i,j})} con i{displaystyle i} y j{displaystyle j} corriendo de 0 a 0 n{displaystyle n}. Cuando la característica del campo de los coeficientes no es dos, generalmente ai,j=aj,i{displaystyle a_{i,j}=a_{j,i} se asume; equivalentemente A=AT{displaystyle A=A^{mathsf {T}. Cuando la característica del campo de los coeficientes es dos, generalmente ai,j=0{displaystyle a_{i,j}=0} es asumido cuando <math alttext="{displaystyle jj.i{displaystyle jtraducido}<img alt="j; equivalente A{displaystyle A} es triangular superior.
La ecuación se puede acortar, ya que la ecuación matricial
- xTAx=0,{displaystyle mathbf {x} {Mathsf {T}Amathbf {x} =0,}
con
- x=()1x1⋯ ⋯ xn)T.{displaystyle mathbf {x} ={begin{pmatrix}1 limitx_{1} Oh, Dios.
La ecuación de la terminación proyectiva es casi idéntica:
- XTAX=0,{displaystyle mathbf {X} {X} =0,}
con
- X=()X0X1⋯ ⋯ Xn)T.{displaystyle mathbf {X} ={begin{pmatrix}X_{0} limitX_{1} limitcdots ¿Qué?
Estas ecuaciones definen una cuádrica como una hipersuperficie algebraica de dimensión n – 1 y grado dos en un espacio de dimensión n.
Se dice que un quadric es no degenerado si la matriz A{displaystyle A} es invertible.
Una cuádrica no degenerada es no singular en el sentido de que su terminación proyectiva no tiene un punto singular (un cilindro no es singular en el espacio afín, pero es una cuádrica degenerada que tiene un punto singular en el infinito).
Los puntos singulares de una cuádrica degenerada son los puntos cuyas coordenadas proyectivas pertenecen al espacio nulo de la matriz A.
Una cuádrica es reducible si y solo si el rango de A es uno (caso de un hiperplano doble) o dos (caso de dos hiperplanos).
Forma normal de cuádricas proyectivas
En el espacio proyectivo real, por la ley de inercia de Sylvester, una forma cuadrática no singular P(X) se puede poner en la forma normal
- P()X)=± ± X02± ± X12± ± ⋯ ⋯ ± ± XD+12{displaystyle P(X)=pm X_{0} {2}pm X_{1}{2}pm cdots pm X_{D+1} {2}
por medio de una transformación proyectiva adecuada (las formas normales para cuádricas singulares pueden tener ceros así como ±1 como coeficientes). Para superficies bidimensionales (dimensión D = 2) en un espacio tridimensional, hay exactamente tres casos no degenerados:
- P()X)={}X02+X12+X22+X32X02+X12+X22− − X32X02+X12− − X22− − X32### {2}######### {2}##############################################################################################################################################################################################################################################
El primer caso es el conjunto vacío.
El segundo caso genera el elipsoide, el paraboloide elíptico o el hiperboloide de dos láminas, dependiendo de si el plano elegido en el infinito corta a la cuádrica en el conjunto vacío, en un punto o en una cónica no degenerada respectivamente. Todos estos tienen curvatura gaussiana positiva.
El tercer caso genera el paraboloide hiperbólico o el hiperboloide de una hoja, dependiendo de si el plano en el infinito lo corta en dos rectas, o en una cónica no degenerada respectivamente. Estas son superficies doblemente regladas de curvatura gaussiana negativa.
La forma degenerada
- X02− − X12− − X22=0.{displaystyle ¿Qué?
genera el cilindro elíptico, el cilindro parabólico, el cilindro hiperbólico o el cono, dependiendo de si el plano en el infinito lo corta en un punto, una recta, dos rectas o una cónica no degenerada respectivamente. Estas son superficies de una sola regla de curvatura gaussiana cero.
Vemos que las transformaciones proyectivas no mezclan curvaturas gaussianas de distinto signo. Esto es cierto para superficies generales.
En el espacio proyectivo complejo, todas las cuádricas no degeneradas se vuelven indistinguibles entre sí.
Parametrización racional
Dado un punto no singular A de una cuádrica, una línea que pasa por A es tangente a la cuádrica, o interseca a la cuádrica exactamente en otro punto (como de costumbre, una línea contenida en la cuádrica se considera tangente, ya que es contenido en el hiperplano tangente). Esto significa que las líneas que pasan por A y no son tangentes a la cuádrica están en correspondencia uno a uno con los puntos de la cuádrica que no pertenecen al hiperplano tangente en A. Expresar los puntos de la cuádrica en términos de la dirección de la línea correspondiente proporciona ecuaciones paramétricas de las siguientes formas.
En el caso de secciones cónicas (curvas cuadráticas), esta pametrización establece una biyección entre una sección cónica proyectiva y una línea proyectiva; esta biyección es un isomorfismo de curvas algebraicas. En dimensiones superiores, la parametrización define un mapa biracional, que es una biyección entre subconjuntos abiertos densos de la cuádrica y un espacio proyectivo de la misma dimensión (la topología que se considera es la habitual en el caso de una cuádrica real o compleja, o la topología de Zariski en todos los casos). Los puntos de la cuádrica que no están en la imagen de esta biyección son los puntos de intersección de la cuádrica y su hiperplano tangente en A.
En el caso afín, la parametrización es una parametrización racional de la forma
- xi=fi()t1,...... ,tn− − 1)f0()t1,...... ,tn− − 1)parai=1,...... ,n,{displaystyle ##### {f_{i}(t_{1},ldotst_{n-1}}{f_{0}(t_{1},ldotst_{n-1}}quad {text{for }i=1,ldotsn,}}
Donde x1,...... ,xn{displaystyle x_{1},ldotsx_{n} son las coordenadas de un punto del quadric, t1,...... ,tn− − 1{displaystyle t_{1},ldotst_{n-1} son parámetros, y f0,f1,...... ,fn{displaystyle F_{0},f_{1},ldotsf_{n} son polinomios de grado en la mayoría de dos.
En el caso proyectivo, la parametrización tiene la forma
- Xi=Fi()T1,...... ,Tn)parai=0,...... ,n,{displaystyle ¿Por qué?
Donde X0,...... ,Xn{displaystyle X_{0},ldotsX_{n} son las coordenadas proyectivas de un punto del quadric, T1,...... ,Tn{displaystyle T_{1},ldots T_{n} son parámetros, y F0,...... ,Fn{displaystyle F_{0},ldots F_{n} son polinomios homogéneos del grado dos.
Uno pasa de una parametrización a la otra poniendo xi=Xi/X0,{displaystyle x_{i}=X_{i}/X_{0} y ti=Ti/Tn:{displaystyle ¿Qué?
- Fi()T1,...... ,Tn)=Tn2fi()T1Tn,...... ,Tn− − 1Tn).{displaystyle ¿Por qué? {T_{1} {T_{n}}}ldots{frac Bueno.
Para calcular la parametrización y probar que los grados son los afirmados, se puede proceder de la siguiente manera en el caso afín. Se puede proceder de manera similar en el caso proyectivo.
Vamos q ser el polinomio cuadrático que define el quadric, y a=()a1,...... an){displaystyle mathbf {a} =(a_{1},ldots a_{n}} ser el vector de coordenadas del punto dado del quadric (así, q()a)=0).{displaystyle q(mathbf {a})=0). } Vamos x=()x1,...... xn){displaystyle mathbf {x} =(x_{1},ldots x_{n}}} ser el vector coordinado del punto del quadric para ser parametrizado, y t=()t1,...... ,tn− − 1,1){displaystyle mathbf {t} =(t_{1},ldotst_{n-1},1)} ser un vector que define la dirección utilizada para la parametrización (las direcciones cuya última coordenadas es cero no se tienen en cuenta aquí; esto significa que algunos puntos del quadric affine no están parametrizados; uno dice a menudo que están parametrizados por puntos en la infinidad en el espacio de parámetros). Los puntos de la intersección del quadric y la línea de dirección t{displaystyle mathbf {t} pasando a{displaystyle mathbf {a} son los puntos x=a+λ λ t{displaystyle mathbf {x} # Mathbf {a} +lambda mathbf {t} tales que
- q()a+λ λ t)=0{displaystyle q(mathbf {a} +lambda mathbf {t}=0}
para algún valor del escalar λ λ .{displaystyle lambda.} Esta es una ecuación del grado dos en λ λ ,{displaystyle lambda} excepto los valores de t{displaystyle mathbf {t} tal que la línea es tangente al quadric (en este caso, el grado es uno si la línea no está incluida en el quadric, o la ecuación se vuelve 0=0{displaystyle 0=0} de otro modo). Los coeficientes de λ λ {displaystyle lambda } y λ λ 2{displaystyle lambda ^{2} son respectivamente de grado en la mayoría de uno y dos en t.{displaystyle mathbf {t} Como coeficiente constante q()a)=0,{displaystyle q(mathbf {a})=0,} la ecuación se vuelve lineal dividiendo por λ λ ,{displaystyle lambda} y su solución única es el cociente de un polinomio de grado en la mayoría uno por un polinomio de grado en la mayoría de dos. Sustituir esta solución en la expresión x,{displaystyle mathbf {x} uno obtiene la parametrización deseada como fracciones de polinomios de grado en la mayoría de dos.
Ejemplo: círculo y esferas
Consideremos la cuádrica de la ecuación
- x12+x22+⋯ ⋯ xn2− − 1=0.{displaystyle x_{1}{2}+x_{2}{2}+cdots x_{n} {2}-1=0}
Para n=2,{displaystyle n=2,} este es el círculo de unidad; n=3{displaystyle n=3} esta es la esfera de unidad; en dimensión superior, esta es la hipersfera de la unidad.
El punto a=()0,...... ,0,− − 1){displaystyle mathbf {a} =(0,ldots0,-1)} pertenece al quadric (la elección de este punto entre otros puntos similares es sólo una cuestión de conveniencia). Entonces, la ecuación q()a+λ λ t)=0{displaystyle q(mathbf {a} +lambda mathbf {t}=0} de la sección anterior
- ()λ λ t12)+⋯ ⋯ +()λ λ tn− − 1)2+()1− − λ λ )2− − 1=0.{displaystyle (lambda) t_{1}{2})+cdots +(lambda t_{n-1} {2}+(1-lambda)}{2}-1=0.}
Ampliando los cuadrados, simplificando los términos constantes, dividiendo λ λ ,{displaystyle lambda} y resolver en λ λ ,{displaystyle lambda} uno obtiene
- λ λ =21+t12+⋯ ⋯ +tn− − 12.{displaystyle lambda ={frac {2}{1+t_{1}{2}+cdots - Sí.
Sustituir esto x=a+λ λ t{displaystyle mathbf {x} # Mathbf {a} +lambda mathbf {t} y simplificando la expresión de la última coordenadas, se obtiene la ecuación paramétrica
- {}x1=2t11+t12+⋯ ⋯ +tn− − 12⋮ ⋮ xn− − 1=2tn− − 11+t12+⋯ ⋯ +tn− − 12xn=1− − t12− − ⋯ ⋯ − − tn− − 121+t12+⋯ ⋯ +tn− − 12.{displaystyle {begin{cases}x_{1}={frac {2t_{1}{1+t_{1}{2}+cdots ¿Qué? \x_{n-1}={frac {2t_{n-1}{1+t_{1}{2}+cdots ################################################################################################################################################################################################################################################################ {1-t_{1} {2}-cdots - ¿Qué? {fn1}} {fnMicrosoft Sans Serif}}
Al homogeneizar se obtiene la parametrización proyectiva
- {}X0=T12+⋯ ⋯ +Tn2X1=2T1Tn⋮ ⋮ Xn− − 1=2Tn− − 1TnXn=Tn2− − T12− − ⋯ ⋯ − − Tn− − 12.{displaystyle {begin{cases}X_{0}=T_{1}{2}+cdots ################################################################################################################################################################################################################################################################ \X_{n-1}=2T_{n-1}T_{n}X_{n}=T_{n}{2}-T_{1}{2}-cdots -T_{n-1} {2}
Una verificación directa muestra que esto induce una bijeción entre los puntos del quadric tal que Xnل ل − − X0{displaystyle X_{n}neq - Sí. y los puntos tales que Tnل ل 0{displaystyle T_{n}neq 0} en el espacio proyectado de los parámetros. Por otro lado, todos los valores de ()T1,...... ,Tn){displaystyle (T_{1},ldotsT_{n}} tales que Tn=0{displaystyle T_{n}=0} y T12+⋯ ⋯ +Tn− − 12ل ل 0{displaystyle T_{1}{2}+cdots ################################################################################################################################################################################################################################################################ 0} dar el punto A.{displaystyle A.}
En el caso de secciones cónicas (n=2{displaystyle n=2}), hay exactamente un punto con Tn=0.{displaystyle T_{n}=0.} y uno tiene una bijección entre el círculo y la línea proyectiva.
Para 2,}" xmlns="http://www.w3.org/1998/Math/MathML">n■2,{displaystyle n título2,}2,}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/1b21deacd0235492da634f2c63e9e705c4bab7fb" style="vertical-align: -0.671ex; width:6.302ex; height:2.509ex;"/> hay muchos puntos con Tn=0,{displaystyle T_{n}=0,} y así muchos valores de parámetro para el punto A.{displaystyle A.} Por otro lado, los otros puntos del quadric para los cuales Xn=− − X0{displaystyle ¿Qué? (y así xn=− − 1{displaystyle x_{n}=-1}) no se puede obtener para cualquier valor de los parámetros. Estos puntos son los puntos de la intersección del quadric y su plano tangente en A.{displaystyle A.} En este caso específico, estos puntos tienen coordenadas complejas no reales, pero basta con cambiar un signo en la ecuación del quadric para producir puntos reales que no se obtienen con la parametrización resultante.
Puntos racionales
Un quadric es definidas un campo F{displaystyle F} si los coeficientes de su ecuación pertenecen a F.{displaystyle F.} Cuando F{displaystyle F} es el campo Q{displaystyle mathbb {Q} de los números racionales, uno puede suponer que los coeficientes son enteros por los denominadores de compensación.
Un punto de un quadric definido sobre un campo F{displaystyle F} se dice racional sobre F{displaystyle F} si sus coordenadas pertenecen a F.{displaystyle F.} Un punto racional sobre el terreno R{displaystyle mathbb {R} de los números reales, se llama un punto real.
Un punto racional Q{displaystyle mathbb {Q} se llama simplemente un punto racional. Al limpiar denominadores, uno puede suponer y uno supone generalmente que las coordenadas proyectivas de un punto racional (en un quadric definido sobre Q{displaystyle mathbb {Q}Son enteros. Además, al limpiar denominadores de los coeficientes, se supone generalmente que todos los coeficientes de la ecuación del quadric y los polinomios que ocurren en la parametrización son enteros.
Encontrar los puntos racionales de una cuádrica proyectiva equivale a resolver una ecuación diofántica.
Dado un punto racional A sobre una cuádrica sobre un campo F, la parametrización descrita en la sección anterior proporciona puntos racionales cuando los parámetros están en F y, a la inversa, cada punto racional de la cuádrica se puede obtener de los parámetros en F, si el punto no está en el hiperplano tangente en A.
Se sigue que, si una cuádrica tiene un punto racional, tiene muchos otros puntos racionales (infinitos si F es infinito), y estos puntos se pueden generar algorítmicamente tan pronto como se conoce uno de ellos.
Como se ha dicho anteriormente, en el caso de las cuádrices proyectivas definidas sobre Q,{displaystyle mathbb {Q} la parametrización toma la forma
- Xi=Fi()T1,...... ,Tn)parai=0,...... ,n,{displaystyle ¿Por qué?
Donde Fi{displaystyle F_{i} son polinomios homogéneos de grado dos con coeficientes enteros. Debido a la homogeneidad, se pueden considerar sólo parámetros que son enteros coprime ajustados. Si Q()X0,...... ,Xn)=0{displaystyle Q(X_{0},ldotsX_{n}=0} es la ecuación del quadric, una solución de esta ecuación se dice primitivo si sus componentes son los enteros de coprime ajustados. Las soluciones primitivas están en una correspondencia con los puntos racionales del quadric (hasta un cambio de signo de todos los componentes de la solución). Las soluciones de enteros no primitivos se obtienen multiplicando soluciones primitivas por enteros arbitrarios, por lo que no merecen un estudio específico. Sin embargo, los parámetros de coprime ajustados pueden producir soluciones no primarias, y uno puede tener que dividir por un divisor más común para llegar a la solución primitiva asociada.
Esto está bien ilustrado por los triples pitagóricos. Un triple pitagórico es un triple ()a,b,c){displaystyle (a,b,c)} de números enteros positivos tal que a2+b2=c2.{displaystyle a^{2}+b^{2}=c^{2} Un triple pitagórico primitivo si a,b,c{displaystyle a,b,c} son coprime ajustado, o, equivalentemente, si alguno de los tres pares ()a,b),{displaystyle (a,b),} ()b,c){displaystyle (b,c)} y ()a,c){displaystyle (a,c)} es coprime.
Por elegir A=()− − 1,0,1),{displaystyle A=(-1,0,1),} el método anterior proporciona la parametrización
- {}a=m2− − n2b=2mnc=m2+m2{begin{cases}a=m^{2}-n^{2}b=2mn\c=m^{2}+m^{2}end{cases}}
para el quadric de la ecuación a2+b2− − c2=0.{displaystyle a^{2}+b^{2}-c^{2}=0} (Los nombres de variables y parámetros se están cambiando de los anteriores a los que son comunes al considerar los triples de Pythagorean).
Si m y n son los enteros coprime tales que n>0,}" xmlns="http://www.w3.org/1998/Math/MathML">m■n■0,{displaystyle m confían confianza0,}n>0,}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/5b51616fbead63c0820310534bcde6e75ebbf47f" style="vertical-align: -0.671ex; width:11.441ex; height:2.509ex;"/> el triple resultante es un triple pitagórico. Si uno de los m y n es incluso y el otro es extraño, este triple resultante es primitivo; de lo contrario, m y n son ambos raros, y uno obtiene un triple primitivo dividiendo por 2.
En resumen, los primitivos Pythagorean triples con b{displaystyle b} incluso se obtienen como
- a=m2− − n2,b=2mn,c=m2+n2,{displaystyle a=m^{2}-n^{2},quad b=2mn,quad c=m^{2}+n^{2},}
con m y n coprime enteros tal que uno es n>0}" xmlns="http://www.w3.org/1998/Math/MathML">m■n■0{displaystyle m confían confianza0}n>0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/a80d02f2a5ba7e75d5878972baa2e8b4359e73c0" style="vertical-align: -0.338ex; width:10.794ex; height:2.176ex;"/> (Esta es la fórmula de Euclid). Los primitivos Pythagorean triples con b{displaystyle b} raro se obtiene como
- a=m2− − n22,b=mn,c=m2+n22,{displaystyle a={frac {m^{2}-n^{2}}}quad b=mn,quad c={frac {m^{2}+n^{2}} {2}}}}
con m y n coprime extraños enteros tal que n>0.}" xmlns="http://www.w3.org/1998/Math/MathML">m■n■0.{displaystyle m confían confianza0.}n>0.}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/a41214fc160145e84fe6750b3a1de0a84d7024fe" style="vertical-align: -0.338ex; width:11.441ex; height:2.176ex;"/>
Como el intercambio de a y b transforma una terna pitagórica en otra terna pitagórica, solo uno de los dos casos es suficiente para producir todas las ternas pitagóricas primitivas.
Cuádricas proyectivas sobre campos
La definición de una cuádrica proyectiva en un espacio proyectivo real (ver arriba) se puede adaptar formalmente definiendo una cuádrica proyectiva en un espacio proyectivo n-dimensional sobre un campo. Para omitir el manejo de coordenadas, una cuádrica proyectiva generalmente se define comenzando con una forma cuadrática en un espacio vectorial.
Forma cuadrática
Vamos K{displaystyle K} ser un campo y V{displaystyle V} un espacio vectorial sobre K{displaystyle K}. Una cartografía q{displaystyle q} desde V{displaystyle V} a K{displaystyle K} tales que
- (Q1) q()λ λ x→ → )=λ λ 2q()x→ → ){displaystyle ;q(lambda {vec {x})=lambda ^{2}q({vec {x});} para cualquier λ λ ▪ ▪ K{displaystyle lambda in K} y x→ → ▪ ▪ V{displaystyle {vec {x}in V}.
- (Q2) f()x→ → ,Sí.→ → ):=q()x→ → +Sí.→ → )− − q()x→ → )− − q()Sí.→ → ){displaystyle ;f({vec {x},{vec {y}):=q({vec {x}+{vec {y}})-q({vec {x})-q({vec {y});} es una forma bilineal.
se llama forma cuadrática. La forma bilineal f{displaystyle f} es simétrico.
En caso de char Kل ل 2{displaystyle operatorname {char} Kneq 2} la forma bilineal es f()x→ → ,x→ → )=2q()x→ → ){displaystyle f({vec {x},{vec {x})=2q({vec} {x}}}, es decir. f{displaystyle f} y q{displaystyle q} se determinan mutuamente de una manera única.
En caso de char K=2{displaystyle operatorname {char} K=2} (Eso significa: 1+1=0{displaystyle 1+1=0}) el formulario bilinear tiene la propiedad f()x→ → ,x→ → )=0{displaystyle f}=0}, es decir. f{displaystyle f} es
simplectic.
Para V=Kn{displaystyle V=K^{n} y x→ → =.. i=1nxie→ → i{displaystyle # {vec {x}=sum} ¿Por qué? {e}_{i}quad}(){}e→ → 1,...... ,e→ → n}{displaystyle {vec {}_{1},ldots{vec {fn} es una base de V{displaystyle V}) q{displaystyle q} tiene la forma familiar
- q()x→ → )=.. 1=i≤ ≤ knaikxixkconaik:=f()e→ → i,e→ → k)paraiل ل kyaii:=q()e→ → i){displaystyle q({vec {x})=sum _{1=ileq K}{n}a_{ik}x_{i}x_{k} {texto {fnK} } a_{ik}:=f {fnMicrosoft Sans Serif} ineq k {text{ and } a_{ii}:=q({vec {e}_{i}) y
- f()x→ → ,Sí.→ → )=.. 1=i≤ ≤ knaik()xiSí.k+xkSí.i){displaystyle f({vec {x},{vec {y})=sum _{1=ileq k}{n}a_{ik}(x_{i}y_{k}+x_{k}y_{i}) }.
Por ejemplo:
- n=3,q()x→ → )=x1x2− − x32,f()x→ → ,Sí.→ → )=x1Sí.2+x2Sí.1− − 2x3Sí.3.{displaystyle n=3,quad q({vec {x})=x_{1}x_{2}-x_{3}^{2},quad f({vec {x}}{vec},{vec {y})=x_{1}y_{2}+x_{2}y_{1}-2x_{3}y_{3};
Espacio proyectivo N-dimensional sobre un campo
Vamos K{displaystyle K} ser un campo, 2≤ ≤ n▪ ▪ N{displaystyle 2leq nin mathbb {N},
- Vn+1{displaystyle V_{n+1} an ()n + 1)-dimensional espacio vectorial sobre el campo K,{displaystyle K,}
- .. x→ → .. {displaystyle langle {vec {x}rangle } el 1-dimensional subespacio generado por 0→ → ل ل x→ → ▪ ▪ Vn+1{displaystyle {vec}neq {vec}in V_{n+1}},
- P={}.. x→ → .. ▪ ▪ x→ → ▪ ▪ Vn+1},{displaystyle {mathcal {}=\\langle {vec}rangle mid {vec {vec {x}in V_{n+1}}} el conjunto de puntos
- G={}Subespacios dimensionales deVn+1},{displaystyle {mathcal {}={text{2-dimensional subespacios de el conjunto de líneas.
- Pn()K)=()P,G){displaystyle P_{n}(K)=({mathcal {P},{mathcal {G}) } es n-dimensional espacio proyectado sobre K{displaystyle K}.
- El conjunto de puntos contenidos en un ()k+1){displaystyle (k+1)}- subespacial dimensional Vn+1{displaystyle V_{n+1} es un k{displaystyle k}- subespacial dimensional de Pn()K){displaystyle P_{n}(K)}. Un subespacio de 2 dimensiones es un avión.
- En caso de 3;}" xmlns="http://www.w3.org/1998/Math/MathML">n■3{displaystyle ;n título3;}
3;}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/57da8d7b5d6230eabbd43311824966d35962d6eb" style="vertical-align: -0.338ex; width:6.946ex; height:2.176ex;"/> a ()n− − 1){displaystyle (n-1)}- subespacio dimensional se llama hiperplano.
Cuádrica proyectiva
Una forma cuadrática q{displaystyle q} en un espacio vectorial Vn+1{displaystyle V_{n+1} define a quadric Q{displaystyle {fnMithcal}} en el espacio proyectado asociado P,{displaystyle {mathcal {}}} como el conjunto de los puntos .. x→ → .. ▪ ▪ P{displaystyle langle {vec {x}rangle in {mathcal {}} tales que q()x→ → )=0{displaystyle q({vec {x})=0}. Eso es,
- Q={}.. x→ → .. ▪ ▪ P▪ ▪ q()x→ → )=0}.{fnMicrosoft Sans {fnMicrosoft Sans Serif} {fnMicrosoft Sans {fnMicrosoft Sans {fnMicrosoft Sans {fnMicrosoft Sans Serif}} {fnMicrosoft Sans {fnMicrosoft Sans {fnMicrosoft Sans Serif} {fnMicrosoft Sans {f}}}}} {f}f}}}}}f}f}}}f}f}fnMicrosigually {f}f}f}fnKf}f}}f}}f}f}f}}f}f}}fnMinMicrosigually {f}}}f}fnMisigual_f} {f}f}fnMinMinMinMinMientras me encantanKf}f}f}f}}fn
Ejemplos en P2()K){displaystyle P_{2}(K)}.:
(E1): Para q()x→ → )=x1x2− − x32{displaystyle ;q({vec {x})=x_{1}x_{2}-x_{3}^{2};} uno obtiene un cónico.
(E2): Para q()x→ → )=x1x2{displaystyle ;q({vec {x})=x_{1}x_{2};} uno obtiene el par de líneas con las ecuaciones x1=0{displaystyle x_{1}=0} y x2=0{displaystyle x_{2}=0}, respectivamente. Se interponen en el punto .. ()0,0,1)T.. {displaystyle langle (0,0,1)^{text{T}rangle };
Para las consideraciones que figuran a continuación se supone que Qل ل ∅ ∅ {displaystyle {mathcal {}neq emptyset }.
Espacio polar
Para punto P=.. p→ → .. ▪ ▪ P{displaystyle P=langle {vec {}rangle in {mathcal {P}} el conjunto
- P⊥ ⊥ :={}.. x→ → .. ▪ ▪ P▪ ▪ f()p→ → ,x→ → )=0}{displaystyle P^{perp }:=wlangle {vec}rangle {mathcal {}mid f({vec {},{vec {x}})=0}
se llama espacio polar P{displaystyle P} (con respecto a q{displaystyle q}).
Si f()p→ → ,x→ → )=0{displaystyle ;f({vec {},{vec {x})=0;} para cualquier x→ → {displaystyle {vec {x}}, uno obtiene P⊥ ⊥ =P{displaystyle P^{perp }={mathcal {}}.
Si f()p→ → ,x→ → )ل ل 0{displaystyle ;f({vec {},{vec {x})neq 0;} por lo menos uno x→ → {displaystyle {vec {x}}, la ecuación f()p→ → ,x→ → )=0{displaystyle ;f({vec {},{vec {x})=0;}es una ecuación lineal no trivial que define un hiperplano. Por lo tanto
- P⊥ ⊥ {displaystyle P^{perp } es un hiperplano o P{displaystyle {fncipal}}.
Intersección con una línea
Para la intersección de una línea arbitraria g{displaystyle g} con un quadric Q{displaystyle {fnMithcal}}, pueden ocurrir los siguientes casos:
- a) g∩ ∩ Q=∅ ∅ {displaystyle gcap {mathcal {}=emptyset;} y g{displaystyle g} se llama exterior
- b) g⊂ ⊂ Q{displaystyle gsubset {Mathcal {Q};} y g{displaystyle g} se llama línea en el quadric
- c) Silenciog∩ ∩ QSilencio=1{fnMicrosoft Sans Serif} y g{displaystyle g} se llama línea tangente
- d) Silenciog∩ ∩ QSilencio=2{fnMicrosoft Sans Serif} y g{displaystyle g} se llama secant line.
Prueba:Vamos g{displaystyle g} ser una línea, que intersecta Q{displaystyle {fnMithcal}} punto U=.. u→ → .. {displaystyle ;U=langle {vec {u}rangle ;} y V=.. v→ → .. {displaystyle ;V=langle {vec {}rangle ;} es un segundo punto g{displaystyle g}.
Desde q()u→ → )=0{displaystyle ;q({vec {u})=0;} uno obtiene
q()xu→ → +v→ → )=q()xu→ → )+q()v→ → )+f()xu→ → ,v→ → )=q()v→ → )+xf()u→ → ,v→ → ).{fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {f} {f} {f} {f}} {f} {f} {f} {f}} {f} {f}} {f}} {v} {v}} {f}} {f} {f}}} {f}}}}} {f}}}}}} {f} {f}}} {f}}} {f} {f}}}}}}}}}}}}}}}}}}}} {f} {f} {f} {f} {f}} {f}}} {f} {f}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {f}}}}}
I) En caso de g⊂ ⊂ U⊥ ⊥ {displaystyle gsubset U^{perp} la ecuación f()u→ → ,v→ → )=0{displaystyle f}=0} sostiene y es
q()xu→ → +v→ → )=q()v→ → ){displaystyle ;q(x{vec {u}+{vec {v})=q({vec {v});} para cualquier x▪ ▪ K{displaystyle xin K}. De aquí o q()xu→ → +v→ → )=0{displaystyle ;q(x{vec {u}+{vec {v})=0;}para cualquiera x▪ ▪ K{displaystyle xin K} o q()xu→ → +v→ → )ل ل 0{displaystyle ;q(x{vec {u}+{vec {v})neq 0;} para cualquiera x▪ ▪ K{displaystyle xin K}, que prueba b) y b').
II) En caso de g⊄U⊥ ⊥ {displaystyle gnot subset U^{perp } uno obtiene f()u→ → ,v→ → )ل ل 0{displaystyle f({vec {u},{vec {v})neq 0} y la ecuación
q()xu→ → +v→ → )=q()v→ → )+xf()u→ → ,v→ → )=0{displaystyle ;q(x{vec {u}+{vec {v})=q({vec {v})+xf({vec {u},{vec {v})=0;} tiene exactamente una solución x{displaystyle x}.
Por lo tanto: Silenciog∩ ∩ QSilencio=2{displaystyle Silenciogcap {fnMithcal {fnK}, que prueba c).
Además, la prueba muestra:
- Una línea g{displaystyle g} a través de un punto P▪ ▪ Q{displaystyle Pin {fn} es un tangente línea si y sólo si g⊂ ⊂ P⊥ ⊥ {displaystyle gsubset P^{perp}.
F-radical, q-radical
En los casos clásicos K=R{displaystyle K=Mathbb {R} o C{displaystyle mathbb {C} sólo existe un radical, debido a char Kل ل 2{displaystyle operatorname {char} Kneq 2} y f{displaystyle f} y q{displaystyle q} están estrechamente conectados. En caso de char K=2{displaystyle operatorname {char} K=2} el quadric Q{displaystyle {fnMithcal}} no se determina por f{displaystyle f} (ver arriba) y así uno tiene que tratar con dos radicales:
- a) R:={}P▪ ▪ P▪ ▪ P⊥ ⊥ =P}{fnMicrosoft Sans Serif} {fnMitcal {fnMicrosoft Sans} }={mathcal {P}} es un subespacio proyectivo. R{displaystyle {fnMithcal}} se llama f- radical de quadric Q{displaystyle {fnMithcal}}.
- b) S:=R∩ ∩ Q{displaystyle {fnMithcal}:={mthcal {R}cap {fnh} {fnK} {}}} se llama singular radical o q{displaystyle q}- radical de Q{displaystyle {fnMithcal}}.
- c) En caso de char Kل ل 2{displaystyle operatorname {char} Kneq 2} uno tiene R=S{displaystyle {fnMithcal}={fnMithcal {S}}.
Un quadric se llama no degenerado si S=∅ ∅ {displaystyle {Mathcal {S}=emptyset }.
Ejemplos en P2()K){displaystyle P_{2}(K)} (véase más arriba):
(E1): Para q()x→ → )=x1x2− − x32{displaystyle ;q({vec {x})=x_{1}x_{2}-x_{3}^{2};} (conic) la forma bilineal es
f()x→ → ,Sí.→ → )=x1Sí.2+x2Sí.1− − 2x3Sí.3.{displaystyle f {vec},{vec} {y})=x_{1}y_{2}+x_{2}y_{1}-2x_{3}y_{3};
En caso de char Kل ل 2{displaystyle operatorname {char} Kneq 2} los espacios polares nunca P{displaystyle {fncipal}}. Por lo tanto R=S=∅ ∅ {displaystyle {fnMithcal}={fnMithcal {S}=emptyset }.
En caso de char K=2{displaystyle operatorname {char} K=2} la forma bilineal se reduce a
f()x→ → ,Sí.→ → )=x1Sí.2+x2Sí.1{displaystyle f {vec},{vec} {y})=x_{1}y_{2}+x_{2}y_{1};} y R=.. ()0,0,1)T.. ∉ ∉ Q{displaystyle {mathcal {R}=langle (0,0,1)^{text{T}rangle notin {mathcal {}}. Por lo tanto Rل ل S=∅ ∅ .{displaystyle {fnMithcal}neq {fnMithcal {S}=emptyset;.}En este caso, f- radical es el punto común de todos los tangentes, el llamado nudo.
En ambos casos S=∅ ∅ {displaystyle S=emptyset } y el quadric (conic) ist no degenerado.
(E2): Para q()x→ → )=x1x2{displaystyle ;q({vec {x})=x_{1}x_{2};} (pair de líneas) la forma bilineal es f()x→ → ,Sí.→ → )=x1Sí.2+x2Sí.1{displaystyle f {vec},{vec} {y})=x_{1}y_{2}+x_{2}y_{1};} y R=.. ()0,0,1)T.. =S,{displaystyle {mathcal {R}=langle (0,0,1) {text{T}rangle ={mathcal {S}; el punto de intersección.
En este ejemplo el quadric es degenerado.
Simetrías
Una cuádrica es un objeto bastante homogéneo:
- Para cualquier punto P∉ ∉ Q∪ ∪ R{displaystyle ¿Por qué? existe una colisión central involutoria σ σ P{displaystyle sigma _{P} con centro P{displaystyle P} y σ σ P()Q)=Q{displaystyle sigma _{mathcal {Q})={mathcal {}}.
Prueba:Due to P∉ ∉ Q∪ ∪ R{displaystyle ¿Por qué? el espacio polar P⊥ ⊥ {displaystyle P^{perp } es un hiperplano.
El mapeo lineal
- φ φ :x→ → → → x→ → − − f()p→ → ,x→ → )q()p→ → )p→ → {displaystyle varphi:{vec {x}}derecha {vec {x}-{frac {f {vec {f},{vec {x}}}}{q({vec {f}}}}{vec {vec {}}}}} {vec}}} {f}}}}} {
induce a un involutorial central collineation σ σ P{displaystyle sigma _{P} con eje P⊥ ⊥ {displaystyle P^{perp } y centro P{displaystyle P} que deja Q{displaystyle {fnMithcal}} invariante.
En el caso de char Kل ل 2{displaystyle operatorname {char} Kneq 2}, la asignación φ φ {displaystyle varphi } produce la forma familiar φ φ :x→ → → → x→ → − − 2f()p→ → ,x→ → )f()p→ → ,p→ → )p→ → {displaystyle ;varphi:{vec {x}derecha {vec {x}-2{frac {f({vec {}},{vec {x})}{f(vec {p},{vec {vec {}}}}}}{vec {vec}}} {vec}}} {vec}}}}}} {f {f {f}{vec}} {vec}} {f {vec}}}}}} {f {f {vec}}}}} {f}}}}}}}} {f {f {f {vec}}}}}}} {f {f}}}}}}} {f {f {f {f {f {f {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {p};} con φ φ ()p→ → )=− − p→ → {displaystyle ;varphi ({vec {p})=-{vec {p} y φ φ ()x→ → )=x→ → {displaystyle ;varphi ({vec {x})={vec {x};} para cualquier .. x→ → .. ▪ ▪ P⊥ ⊥ {displaystyle langle {vec {x}rangle in P^{perp}.
Observación:
- a) Una línea exterior, una línea tangente o una línea de secant es mapeado por la involución σ σ P{displaystyle sigma _{P} en una línea exterior, tangente y secant respectivamente.
- b) R{displaystyle {fnMithcal}} es un punto fijo por σ σ P{displaystyle sigma _{P}.
Q-subespacios e índice de una cuádrica
Un subespacio U{displaystyle; {fnMitcal};} de Pn()K){displaystyle P_{n}(K)} se llama q{displaystyle q}- Subespacial si U⊂ ⊂ Q{displaystyle ;{mathcal {U}subset {mathcal};}
Por ejemplo: puntos en una esfera o líneas en un hiperboloide (ver abajo).
- Dos. maximal q{displaystyle q}- los subespacios tienen la misma dimensión m{displaystyle m}.
Vamos. m{displaystyle m} la dimensión del maximal q{displaystyle q}- Subespacios de Q{displaystyle {fnMithcal}} entonces
- El entero i:=m+1{displaystyle ;i:=m+1;} se llama índice de Q{displaystyle {fnMithcal}}.
Teorema: (BUEKENHOUT)
- Para el índice i{displaystyle i} de un quadric no degenerado Q{displaystyle {fnMithcal}} dentro Pn()K){displaystyle P_{n}(K)} lo siguiente es cierto:
- i≤ ≤ n+12{displaystyle ileq {fnMicroc {n+1}{2}}.
Vamos. Q{displaystyle {fnMithcal}} un quadric no degenerado en Pn()K),n≥ ≥ 2{displaystyle P_{n}(K),ngeq 2}, y i{displaystyle i} su índice.
- En caso de i=1{displaystyle i=1} quadric Q{displaystyle {fnMithcal}} se llama esfera (o conic oval si n=2{displaystyle n=2}).
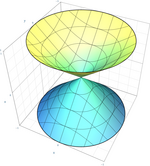
- En caso de i=2{displaystyle i=2} quadric Q{displaystyle {fnMithcal}} se llama hiperboloide (de una hoja).
Ejemplos:
- a) Quadric Q{displaystyle {fnMithcal}} dentro P2()K){displaystyle P_{2}(K)} con forma q()x→ → )=x1x2− − x32{displaystyle ;q({vec {x})=x_{1}x_{2}-x_{3}^{2};} no es degenerado con el índice 1.
- b) Si es polinomio p().. )=.. 2+a0.. +b0{displaystyle ;p(xi)=xi ^{2}+a_{0}xi # es irreducible sobre K{displaystyle K} la forma cuadrática q()x→ → )=x12+a0x1x2+b0x22− − x3x4{displaystyle ;q({vec {x})=x_{1}{2}+a_{0}x_{1}x_{2}+b_{0}x_{2}{2}-x_{3}x_{4};} da lugar a un quadric no degenerado Q{displaystyle {fnMithcal}} dentro P3()K){displaystyle P_{3}(K)} del índice 1 (foto). Por ejemplo: p().. )=.. 2+1{displaystyle ;p(xi)=xi ^{2}+1;} es irreducible sobre R{displaystyle mathbb {R} (pero no terminó) C{displaystyle mathbb {C}!).
- c) En P3()K){displaystyle P_{3}(K)} la forma cuadrática q()x→ → )=x1x2+x3x4{displaystyle ;q({vec {x})=x_{1}x_{2}+x_{3}x_{4};} genera un hiperboloide.
Generalización de cuádricas: conjuntos cuadráticos
No es razonable extender formalmente la definición de cuádricas a espacios sobre campos sesgados genuinos (anillos de división). Porque uno obtendría secantes con más de 2 puntos de la cuádrica que es totalmente diferente de las cuádricas habituales. La razón es la siguiente afirmación.
- Un anillo de división K{displaystyle K} es conmutativo si y sólo si cualquier ecuación x2+ax+b=0,a,b▪ ▪ K{displaystyle x^{2}+ax+b=0, a,bin K}, tiene en la mayoría de dos soluciones.
Hay generalizaciones de cuádricas: conjuntos cuadráticos. Un conjunto cuadrático es un conjunto de puntos de un espacio proyectivo con las mismas propiedades geométricas que un conjunto cuadrático: cada línea corta un conjunto cuadrático en dos puntos como máximo o está contenida en el conjunto.
Contenido relacionado
Sistema ortocéntrico
Grupo gratis
Elemento principal