Cuadratura del circulo

Equiparando el círculo: las áreas de este cuadrado y este círculo son iguales a π π {displaystyle pi}. En 1882, se comprobó que esta figura no se puede construir en un número finito de pasos con una brújula idealizada y una recta.

La cuadratura del círculo es un problema de geometría propuesto por primera vez en las matemáticas griegas. Es el desafío de construir un cuadrado con el área de un círculo usando solo un número finito de pasos con una regla y un compás. La dificultad del problema planteó la cuestión de si los axiomas específicos de la geometría euclidiana relativos a la existencia de líneas y círculos implicaban la existencia de dicho cuadrado.

En 1882, la tarea fue demostrada como imposible, como consecuencia del teorema Lindemann-Weierstrass, que demuestra que pi (π π {displaystyle pi}) es un número trascendental. Eso es, π π {displaystyle pi} no es la raíz de ningún polinomio con coeficientes racionales. Se ha sabido desde hace décadas que la construcción sería imposible π π {displaystyle pi} fueron trascendentales, pero ese hecho no fue probado hasta 1882. Existen construcciones aproximadas con cualquier precisión no perfecta dada, y se han encontrado muchas de esas construcciones.

A pesar de la prueba de que es imposible, los intentos de cuadratura del círculo han sido comunes en las pseudomatemáticas (es decir, el trabajo de los chiflados matemáticos). La expresión "la cuadratura del círculo" a veces se usa como una metáfora para tratar de hacer lo imposible. El término cuadratura del círculo a veces se usa como sinónimo de cuadratura del círculo, pero también puede referirse a métodos aproximados o numéricos para encontrar el área de un círculo.

Historia

Los métodos para calcular el área aproximada de un círculo dado, que se puede considerar como un problema precursor para cubrir el círculo, ya se conocían en muchas culturas antiguas. Estos métodos pueden resumirse indicando la aproximación a π que producen. En alrededor de 2000 a.C., los matemáticos babilónicos utilizaron la aproximación π π .. 258=3.125{displaystyle pi approx {25}=3.125}, y aproximadamente al mismo tiempo los antiguos matemáticos egipcios utilizados π π .. 25681.. 3.16{displaystyle pi approx {256}approx 3.16}. Más de 1000 años después, el Antiguo Testamento Libros de Reyes utilizado la aproximación más simple π π .. 3{displaystyle pi approx 3}. Matemáticas indias antiguas, como se registra en Shatapatha Brahmana y Shulba Sutras, utilizado varias aproximaciones diferentes a π π {displaystyle pi}. Arquímedes demostró una fórmula para el área de un círculo, según la cual <math alttext="{displaystyle 3,{tfrac {10}{71}}approx 3.141<pi 31071.. 3.141.π π .317.. 3.143{displaystyle 3,{tfrac {10}}approx 3.141traducidopi} {fnMicroc {1}}approx 3.143}<img alt="{displaystyle 3,{tfrac {10}{71}}approx 3.141<pi . En matemáticas chinas, en el siglo III CE, Liu Hui encontró aproximaciones aún más precisas utilizando un método similar al de Arquímedes, y en el siglo V Zu Chongzhi encontrado π π .. 355/113.. 3.141593{displaystyle pi approx 355/113approx 3.141593}, una aproximación conocida como Milü.

El problema de construir un cuadrado cuya área sea exactamente la de un círculo, en lugar de una aproximación a él, proviene de las matemáticas griegas. Los matemáticos griegos encontraron construcciones con compás y regla para convertir cualquier polígono en un cuadrado de área equivalente. Usaron esta construcción para comparar áreas de polígonos geométricamente, en lugar de hacerlo mediante el cálculo numérico del área que sería más típico en las matemáticas modernas. Como escribió Proclo muchos siglos después, esto motivó la búsqueda de métodos que permitieran hacer comparaciones con formas no poligonales:

Algunas soluciones parciales aparentes dieron falsa esperanza durante mucho tiempo. En esta figura, la figura sombreada es la luna de los Hipócrates. Su área es igual a la zona del triángulo ABC (fundada por Hipócrates de Chios).

El primer griego conocido que estudió el problema fue Anaxágoras, quien trabajó en él mientras estaba en prisión. Hipócrates de Quíos atacó el problema encontrando una forma delimitada por arcos circulares, la luna de Hipócrates, que podía ser cuadrada. Antiphon the Sofist creía que inscribir polígonos regulares dentro de un círculo y duplicar el número de lados eventualmente llenaría el área del círculo (este es el método de agotamiento). Dado que cualquier polígono puede elevarse al cuadrado, argumentó, el círculo puede elevarse al cuadrado. Por el contrario, Eudemus argumentó que las magnitudes no se pueden dividir sin límite, por lo que el área del círculo nunca se agotaría. Al mismo tiempo que Antiphon, Bryson de Heraclea argumentó que, dado que existen círculos más grandes y más pequeños, debe haber un círculo de igual área; este principio puede verse como una forma del teorema moderno del valor intermedio. El objetivo más general de llevar a cabo todas las construcciones geométricas utilizando solo un compás y una regla se ha atribuido a menudo a Enópides, pero la evidencia de esto es circunstancial.

El problema de encontrar el área bajo una curva arbitraria, ahora conocido como integración en cálculo o cuadratura en análisis numérico, se conocía como cuadrado antes de la invención del cálculo. Dado que se desconocían las técnicas del cálculo, en general se presumía que un cuadrado debía hacerse mediante construcciones geométricas, es decir, con compás y regla. Por ejemplo, Newton escribió a Oldenburg en 1676 'Creo que a M. Leibnitz no le disgustará el teorema hacia el comienzo de mi carta pag. 4 para cuadrar líneas curvas geométricamente". En las matemáticas modernas, los términos han divergido en significado, y la cuadratura generalmente se usa cuando se permiten métodos de cálculo, mientras que elevar al cuadrado la curva conserva la idea de usar solo métodos geométricos restringidos.

James Gregory intentó probar la imposibilidad de cubrir el círculo en Vera Circuli et Hyperbolae Quadratura (El Escuadrón Verdadero del Círculo y del Hiperbola) en 1667. Aunque su prueba fue defectuosa, fue el primer papel en intentar resolver el problema utilizando propiedades algebraicas de π π {displaystyle pi}. Johann Heinrich Lambert demostró en 1761 que π π {displaystyle pi} es un número irracional. No fue hasta 1882 que Ferdinand von Lindemann logró probar con más fuerza que π es un número trascendental, y al hacerlo también demostró la imposibilidad de cubrir el círculo con brújula y rectitud.

Una historia parcial de Florian Cajori de los intentos del problema.

Después de la demostración de la imposibilidad de Lindemann, se consideró que el problema había sido resuelto por matemáticos profesionales, y su historia matemática posterior está dominada por intentos pseudomatemáticos de construcciones de círculos cuadrados, en su mayoría por aficionados, y por la desacreditación de estos esfuerzos.. Además, varios matemáticos posteriores, incluido Srinivasa Ramanujan, desarrollaron construcciones con regla y compás que aproximan el problema con precisión en unos pocos pasos.

Otros dos problemas clásicos de la antigüedad, famosos por su imposibilidad, eran doblar el cubo y trisecar el ángulo. Al igual que la cuadratura del círculo, estos no se pueden resolver con regla y compás. Sin embargo, tienen un carácter diferente a la cuadratura del círculo, ya que su solución involucra la raíz de una ecuación cúbica, en lugar de ser trascendental. Por lo tanto, se pueden usar métodos más poderosos que las construcciones con compás y regla, como la construcción neusis o el plegado de papel matemático, para construir soluciones a estos problemas.

Imposibilidad

La solución del problema de escuadrar el círculo por brújula y escalera requiere la construcción del número π π {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {\fnMicrosoft {\\fnMicrosoft {\fnMicrosoft {fnMicrosoft {\fnMicrosoft {\fnMicrosoft {\\fnMicrosoft {\\\\\\\fnMicrosoft {\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\fn\\\\\\\\\\\\\\\\\\\\\\\\\\\fn }, la longitud del lado de un cuadrado cuyo área iguala la de un círculo de unidad. Si π π {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {\fnMicrosoft {\\fnMicrosoft {\fnMicrosoft {fnMicrosoft {\fnMicrosoft {\fnMicrosoft {\\fnMicrosoft {\\\\\\\fnMicrosoft {\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\fn\\\\\\\\\\\\\\\\\\\\\\\\\\\fn } eran un número constructible, que seguiría de la brújula estándar y construcciones de escaleras que π π {displaystyle pi} también sería constructible. En 1837, Pierre Wantzel mostró que las longitudes que podrían construirse con brújula y rectitud tenían que ser soluciones de ciertas ecuaciones polinómicas con coeficientes racionales. Así, longitudes constructibles deben ser números algebraicos. Si el círculo podría ser cuadrado usando solamente brújula y rectitud, entonces π π {displaystyle pi} tendría que ser un número algebraico. No fue hasta 1882 que Ferdinand von Lindemann demostró la trascendencia de π π {displaystyle pi} y así mostró la imposibilidad de esta construcción. La idea de Lindemann era combinar la prueba de la trascendencia del número de Euler e{displaystyle e}, mostrado por Charles Hermite en 1873, con la identidad de Euler

eiπ π =− − 1.{displaystyle e^{ipi} }=-1.}

π π {displaystyle pi}

e{displaystyle e}

π π {displaystyle pi}

Doblar las reglas mediante la introducción de una herramienta complementaria, lo que permite un número infinito de operaciones de compás y regla o realizando las operaciones en ciertas geometrías no euclidianas hace que la cuadratura del círculo sea posible en cierto sentido. Por ejemplo, Dinostratos' El teorema usa la cuadratriz de Hipias para cuadrar el círculo, lo que significa que si esta curva ya está dada de alguna manera, entonces se puede construir un cuadrado y un círculo de áreas iguales a partir de ella. La espiral de Arquímedes se puede utilizar para otra construcción similar. Aunque el círculo no se puede cuadrar en el espacio euclidiano, a veces puede serlo en geometría hiperbólica bajo interpretaciones adecuadas de los términos. El plano hiperbólico no contiene cuadrados (cuadriláteros con cuatro ángulos rectos y cuatro lados iguales), sino que contiene cuadriláteros regulares, formas con cuatro lados iguales y cuatro ángulos iguales más agudos que los ángulos rectos. Existen en el plano hiperbólico (contable) infinitamente muchos pares de círculos construibles y cuadriláteros regulares construibles de igual área, que, sin embargo, se construyen simultáneamente. No existe un método para comenzar con un cuadrilátero regular arbitrario y construir el círculo de igual área. Simétricamente, no existe un método para comenzar con un círculo arbitrario y construir un cuadrilátero regular de igual área, y para círculos suficientemente grandes no existe tal cuadrilátero.

Construcciones aproximadas

Aunque es imposible cubrir el círculo exactamente con brújula y rectitud, se pueden dar aproximaciones para cubrir el círculo mediante la construcción de longitudes cercanas a π π {displaystyle pi}. Sólo se necesita geometría elemental para convertir cualquier aproximación racional dada π π {displaystyle pi} en una brújula y construcción de hendiduras correspondientes, pero tales construcciones tienden a ser muy largas en comparación con la precisión que logran. Después de que el problema exacto se probó insolvable, algunos matemáticos aplicaron su ingenio para encontrar aproximaciones para cubrir el círculo que son particularmente simples entre otras construcciones imaginables que dan una precisión similar.

Construcción por Kochański

Construcción aproximada de Kochański

Continuación con círculo y cuadrado de la misma zona; r{displaystyle r} denota el radio inicial

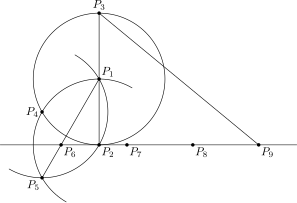
Una de las construcciones de brújula aproximada históricas tempranas es de un documento de 1685 del jesuita polaco Adamandy Kochański, produciendo una aproximación divergiendo de π π {displaystyle pi} en el quinto lugar decimal. Aunque las aproximaciones numéricas mucho más precisas π π {displaystyle pi} eran ya conocidos, la construcción de Kochański tiene la ventaja de ser bastante simple. En el diagrama izquierdo

SilencioP3P9Silencio=SilencioP1P2Silencio403− − 23.. 3.141533338⋅ ⋅ SilencioP1P2Silencio.. π π r.{displaystyle - ¿Qué? 3.141,5{color {red}33,338}cdot Silencio. pi r.}

para π π {displaystyle pi}.

Construcciones con 355/113

Construcción de Jacob de Gelder 355/113

Construcción de Ramanujan 355/113

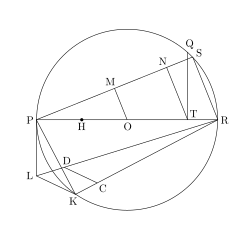
Jacob de Gelder publicó en 1849 una construcción basada en la aproximación

π π .. 355113=3.141592920...... {displaystyle pi approx {355}=3.141;592{color {red};920;ldots}}

Gelder no construyó el lado del cuadrado; le bastó encontrar el valor

AH̄ ̄ =4272+82.{displaystyle {fnK}={fnMic} {4^{2}{7^{2}+8^{2}}}

En 1914, el matemático indio Srinivasa Ramanujan dio otra construcción geométrica para la misma aproximación.

Construcciones usando la proporción áurea

Construcción de la relación de oro de Hobson

Construcción de la relación de oro de Dixon

Construcción de 13 pasos de Beatrix

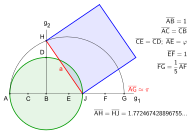
Una construcción aproximada realizada por E. W. Hobson en 1913 tiene una precisión de tres decimales. La construcción de Hobson corresponde a un valor aproximado de

65⋅ ⋅ ()1+φ φ )=3.141640...... ,{displaystyle {frac {6}{5}cdot left(1+varphi right)=3.141;{color {red}640;ldots }}

φ φ {displaystyle varphi }

φ φ =()1+5)/2{displaystyle varphi =(1+{sqrt {5}}/2}

El mismo valor aproximado aparece en una construcción de 1991 de Robert Dixon. En 2022 Frédéric Beatrix presentó una construcción geométrica en 13 pasos.

Segunda construcción por Ramanujan

Cuadrando el círculo, construcción aproximada según Ramanujan de 1914, con continuación de la construcción (líneas decoradas, línea roja proporcional), ver animación.

Sketch of "Manuscript book 1 of Srinivasa Ramanujan" p. 54

En 1914, Ramanujan dio una construcción que equivalía a tomar el valor aproximado para π π {displaystyle pi} para ser

()92+19222)14=2143224=3.141592652582...... {displaystyle left(9^{2}+{frac {19^{2}{22}right)^{frac} {1}{4}={sqrt[{4}{frac {2143}{22}}=3.141;592;65{color} {c}}}}=3.141;592; {red}2;582;ldots}

π π {displaystyle pi}

Construcciones incorrectas

En su vejez, el filósofo inglés Thomas Hobbes se convenció de que había logrado cubrir el círculo, una afirmación refutada por John Wallis como parte de la controversia de Hobbes-Wallis. Durante el siglo XVIII y XIX, las falsas nociones de que el problema de escudriñar el círculo estaba relacionado de alguna manera con el problema de la longitud, y que una gran recompensa se daría para una solución, se hizo prevaleciente entre los cuadrados círculos que serían. En 1851, John Parker publicó un libro Cuadrícula del Círculo en el que afirmó haber cuadrado el círculo. Su método realmente produjo una aproximación π π {displaystyle pi} exacto a seis dígitos.

El matemático, lógico y escritor de la era victoriana Charles Lutwidge Dodgson, más conocido por su seudónimo Lewis Carroll, también expresó interés en desacreditar las teorías ilógicas del cuadrado del círculo. En una de las entradas de su diario de 1855, Dodgson enumeró los libros que esperaba escribir, incluido uno llamado "Hechos claros para los cuadráticos". En la introducción a "A New Theory of Parallels", Dodgson relató un intento de demostrar errores lógicos a un par de cuadráticos, afirmando:

Una ridiculización de la cuadratura del círculo aparece en el libro de Augustus De Morgan A Budget of Paradoxes, publicado póstumamente por su viuda en 1872. Habiendo publicado originalmente el trabajo como una serie de artículos en The Athenaeum, lo estaba revisando para su publicación en el momento de su muerte. La cuadratura de círculos perdió popularidad después del siglo XIX, y se cree que el trabajo de De Morgan ayudó a lograrlo.

Libro de Heisel 1934

Incluso después de que se hubiera demostrado imposible, en 1894, el matemático amateur Edwin J. Goodwin afirmó que había desarrollado un método para cuadrar el círculo. La técnica que desarrolló no cuadraba con precisión el círculo, y proporcionaba un área incorrecta del círculo que esencialmente redefinió π π {displaystyle pi} igual a 3.2. Goodwin propuso entonces el proyecto de ley de Indiana Pi en la legislatura estatal de Indiana permitiendo al estado utilizar su método en la educación sin pagarle las regalías. El proyecto de ley pasó sin objeciones en la casa estatal, pero el proyecto de ley fue presentado y nunca votado en el Senado, en medio de aumentar el ridículo de la prensa.

El chiflado matemático Carl Theodore Heisel también afirmó haber logrado la cuadratura del círculo en su libro de 1934, "¡He aquí!: el gran problema ya no queda sin resolver: la cuadratura del círculo más allá de toda refutación." Paul Halmos se refirió al libro como un "libro clásico de chiflados".

En la literatura

El problema de la cuadratura del círculo se ha mencionado en una amplia gama de épocas literarias, con una variedad de significados metafóricos. Su uso literario se remonta al menos al 414 a. C., cuando se representó por primera vez la obra Los pájaros de Aristófanes. En él, el personaje Metón de Atenas menciona la cuadratura del círculo, posiblemente para indicar la naturaleza paradójica de su ciudad utópica.

Vitruvian Man

El Paraíso de Dante, canto XXXIII, líneas 133–135, contiene el verso:

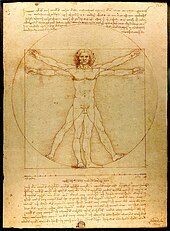
Para Dante, la cuadratura del círculo representa una tarea más allá de la comprensión humana, que él compara con su propia incapacidad para comprender el Paraíso. La imagen de Dante también recuerda un pasaje de Vitruvio, famosamente ilustrado más tarde en el Hombre de Vitruvio de Leonardo da Vinci, de un hombre inscrito simultáneamente en un círculo y un cuadrado. Dante usa el círculo como símbolo de Dios, y puede haber mencionado esta combinación de formas en referencia a la naturaleza divina y humana simultánea de Jesús. Anteriormente, en el canto XIII, Dante llama a Bryson, el cuadrado del círculo griego, por haber buscado el conocimiento en lugar de la sabiduría.

Varias obras de la poetisa del siglo XVII Margaret Cavendish profundizan en el problema de la cuadratura del círculo y sus significados metafóricos, incluido un contraste entre la unidad de la verdad y el faccionalismo, y la imposibilidad de racionalizar "la fantasía y la naturaleza femenina". En 1742, cuando Alexander Pope publicó el cuarto libro de su Dunciad, los intentos de cuadratura del círculo se consideraban "salvajes e infructuosos":

Del mismo modo, la ópera cómica de Gilbert and Sullivan Princess Ida presenta una canción que enumera satíricamente los objetivos imposibles de la universidad de mujeres dirigida por el personaje principal, como encontrar el movimiento perpetuo. Uno de estos objetivos es "Y el círculo: lo cuadrarán/Algún buen día".

Se ha dicho que la sextina, una forma poética utilizada por primera vez en el siglo XII por Arnaut Daniel, cuadra metafóricamente el círculo en su uso de un número cuadrado de líneas (seis estrofas de seis líneas cada una) con un esquema circular de seis palabras repetidas. Spanos (1978) escribe que esta forma invoca un significado simbólico en el que el círculo representa el cielo y el cuadrado representa la tierra. Una metáfora similar se usó en 'Squaring the Circle', un cuento de 1908 de O. Henry, sobre una larga enemistad familiar. En el título de esta historia, el círculo representa el mundo natural, mientras que el cuadrado representa la ciudad, el mundo del hombre.

En trabajos posteriores, los cuadrangulares como Leopold Bloom en la novela Ulysses de James Joyce y el abogado Paravant en The Magic Mountain de Thomas Mann son vistos como tristemente engañados o como soñadores no mundanos, inconscientes de su imposibilidad matemática y haciendo planes grandiosos para un resultado que nunca alcanzarán.

Lecturas adicionales y enlaces externos