Cuadratura de la parábola

Quadrature of the Parabola (Greek: THετραγωνισμ errorς παραβολ raceς) es un tratado sobre la geometría, escrito por Arquímedes en el siglo III a.C. y dirigido a su conocido de Alejandría Dositheus. Contiene 24 proposiciones relativas al parabolas, culminando en dos pruebas que muestran que la zona de un segmento parabólico (la región encerrada por una parabola y una línea) es ${\fnMicroc} {4}{3}}$ la de un triángulo inscrito.

Es una de las obras más conocidas de Arquímedes, en particular por su ingenioso uso del método exhaustivo y en la segunda parte de una serie geométrica. Arquímedes disecciona el área en infinitos triángulos cuyas áreas forman una progresión geométrica. Luego calcula la suma de la serie geométrica resultante y demuestra que esta es el área del segmento parabólico. Esto representa el uso más sofisticado de un argumento de reducción al absurdo en las matemáticas de la antigua Grecia, y la solución de Arquímedes permaneció insuperable hasta el desarrollo del cálculo integral en el siglo XVII, siendo reemplazada por la fórmula de cuadratura de Cavalieri.

A segmento parabólico es la región atada por una parabola y línea. Para encontrar el área de un segmento parabólico, Arquímedes considera un cierto triángulo inscrito. La base de este triángulo es el acorde dado de la parabola, y el tercer vértice es el punto en la parabola tal que el tangente a la parabola en ese punto es paralelo al acorde. La Proposición 1 del trabajo establece que una línea del tercer vértice dibujada paralelamente al eje divide el acorde en segmentos iguales. El teorema principal afirma que la zona del segmento parabólico es ${\fnMicroc} {4}{3}}$ el del triángulo inscrito.

Las secciones cónicas, como la parábola, ya eran bien conocidas en la época de Arquímedes gracias a Menecmo un siglo antes. Sin embargo, antes de la llegada del cálculo diferencial e integral, no existían métodos sencillos para calcular el área de una sección cónica. Arquímedes proporciona la primera solución documentada a este problema, centrándose específicamente en el área delimitada por una parábola y una cuerda.Arquímedes ofrece dos demostraciones del teorema principal: una mediante mecánica abstracta y la otra mediante geometría pura. En la primera, Arquímedes considera una palanca en equilibrio bajo la acción de la gravedad, con segmentos ponderados de una parábola y un triángulo suspendido de los brazos de una palanca a distancias específicas del fulcro. Cuando se conoce el centro de gravedad del triángulo, el equilibrio de la palanca da como resultado el área de la parábola en función del área del triángulo con la misma base y la misma altura. Arquímedes se desvía aquí del procedimiento de Sobre el equilibrio de los planos, ya que sitúa los centros de gravedad a un nivel inferior al de la balanza. 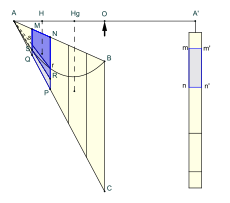La segunda, y más famosa, prueba utiliza geometría pura, en particular la suma de una serie geométrica.De las veinticuatro proposiciones, las tres primeras se citan sin demostración de los Elementos de las Cónicas de Euclides (una obra perdida de Euclides sobre secciones cónicas). Las proposiciones 4 y 5 establecen las propiedades elementales de la parábola. Las proposiciones 6 a 17 proporcionan la demostración mecánica del teorema principal; las proposiciones 18 a 24 presentan la demostración geométrica.

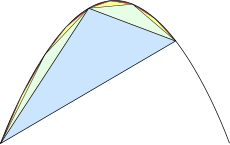
La idea principal de la demostración es la disección del segmento parabólico en infinitos triángulos, como se muestra en la figura de la derecha. Cada uno de estos triángulos está inscrito en su propio segmento parabólico, de la misma manera que el triángulo azul está inscrito en el segmento mayor.

En proposiciones dieciocho a veintiuno, Arquímedes demuestra que el área de cada triángulo verde es ${\fnMicroc} {1}{8}}$ el área del triángulo azul, por lo que ambos triángulos verdes juntos suma a ${\fnMicroc} {1}{4}}$ el área del triángulo azul. Desde un punto de vista moderno, esto es porque el triángulo verde tiene ${\fnMicroc} {1}{2}}}$ el ancho y ${\fnMicroc} {1}{4}}$ la altura del triángulo azul:

Siguiendo el mismo argumento, cada uno de los ${\displaystyle 4}$ triángulos amarillos tiene ${\fnMicroc} {1}{8}}$ el área de un triángulo verde o ${\displaystyle {\tfrac {1}{64}}}$ el área del triángulo azul, resumiendo a ${\displaystyle {\tfrac {4}{64}={\tfrac} {1}{16}}$ el área del triángulo azul; cada uno de los ${\displaystyle 2^{3}=8}$ triángulos rojos tiene ${\fnMicroc} {1}{8}}$ el área de un triángulo amarillo, resumiendo a ${\displaystyle {\tfrac {2}{8^{3}}={\tfrac}} {\tfrac}} {\c\c\cH0}} {1}{64}}}$ el área del triángulo azul; etc. Utilizando el método de agotamiento, se deduce que el área total del segmento parabólico es dada por

${\displaystyle {\text{Area}\;=\;T\,+\,{\frac} {1}{4}T\,+\,{\frac {1}{4}} {\c} {\c}} T\,+\,{4^{3} T\,+\,\cdots.}$

Aquí, T representa el área del triángulo azul grande, el segundo término representa el área total de los dos triángulos verdes, el tercer término representa el área total de los cuatro triángulos amarillos, y así sucesivamente. Esto se simplifica para obtener:

$[\displaystyle {\text{Area}}\;=\;\left(1\,+\,{\frac {1}{4}}\,+\,{\frac {1}{16}\,+\,{\frac {1}{64}\,+\,\cdots\right) T.}$

Para completar la prueba, Arquímedes demuestra que

${\displaystyle 1\,+\,{\frac {1}{4}\,+\,{16}\\,+\,{\frac {1}{64}\,+\,\cdots \;=\;{\frac}\fnMicroc {1}}\,+\,\cdots\; {4}{3}}$

La fórmula anterior es una serie geométrica: cada término sucesivo es un cuarto del término anterior. En matemáticas modernas, esta fórmula es un caso especial de la fórmula de la suma para una serie geométrica.Arquímedes calcula la suma utilizando un método completamente geométrico, ilustrado en la imagen adyacente. Esta imagen muestra un cuadrado unitario dividido en una infinidad de cuadrados más pequeños. Cada cuadrado morado sucesivo tiene un cuarto del área del cuadrado anterior, siendo el área total morada la suma.

${\displaystyle {\frac {4}\,+\,{\frac {1}}\,+\,{\frac {1}{64}}\,+\,\cdots.}$

Sin embargo, los cuadrados púrpura son congruentes a cualquiera de los conjuntos de cuadrados amarillos, y así cubren ${\fnMicroc} {1}{3}}$ de la zona de la plaza unidad. Se sigue que la serie anterior suma a ${\fnMicroc} {4}{3}}$ (since ${\displaystyle 1+{}{3}={\tfrac {4}{3}}$).

• Cuadrícula (geometría)
• Historia del cálculo

• Ajose, Domingo y Roger Nelsen (junio de 1994). "Proof sin Palabras: Serie geométrica". Revista Matemática. 67 (3): 230. doi:10.2307/2690617. JSTOR 2690617.
• Ancora, Luciano (2014). "Quadrature of the parabola with the square pyramidal number". Archimede. 66 3).
• Bressoud, David M. (2006). A Radical Approach to Real Analysis (2a edición). Asociación Matemática de América. ISBN 0-88385-747-2..
• Dijksterhuis, E.J. (1987) "Archimedes", Princeton U. Press ISBN 0-691-08421-1
• Edwards Jr., C. H. (1994). El desarrollo histórico del cálculo (3a edición). Springer. ISBN 0-387-94313-7..
• Heath, Thomas L. (2011). Obras de Arquímedes (2a edición). CreateSpace. ISBN 978-1-4637-4473-1.
• Simmons, George F. (2007). Calculus Gems. Asociación Matemática de América. ISBN 978-0-88385-561-4..
• Stein, Sherman K. (1999). Arquímedes: ¿Qué hizo además de Cry Eureka?. Asociación Matemática de América. ISBN 0-88385-718-9.
• Stillwell, John (2004). Matemáticas y su historia (2a edición). Springer. ISBN 0-387-95336-1..
• Swain, Gordon y Thomas Dence (abril de 1998). "Cuadrícula de Arquimedes de la Parabola Revisitada". Revista Matemática. 71 2): 123–30. doi:10.2307/2691014. JSTOR 2691014.
• Wilson, Alistair Macintosh (1995). El Infinito en la Finita. Oxford University Press. 0-19-853950-9..

• Casselman, Bill. "La cuadratura de Arquimedes de la parabola". Archivado desde el original el 2012-02-04. Texto completo, traducido por T.L. Heath.
• Xavier University Department of Mathematics and Computer Science. "Arquimedes of Syracuse". Archivado desde el original en 2016-01-13.. Texto de las proposiciones 1–3 y 20–24, con comentario.
• http://planetmath.org/ArchimedesCalculus