Cuadrado mágico
Los sumos de cada fila, columna y diagonales principales son iguales

El caso más pequeño (y único hasta la rotación y la reflexión) no-trivial de una plaza mágica, orden 3
En matemáticas recreativas, una serie cuadrada de números, generalmente números enteros positivos, se llama un cuadrado si las sumas de los números en cada fila, cada columna, y ambas diagonales principales son las mismas. El 'orden' de la plaza mágica es el número de enteros a lo largo de un lado (n), y la suma constante se llama "la constante mágica". Si el array incluye sólo los enteros positivos 1,2,...,n2{displaystyle 1,2,...,n^{2} Se dice que la plaza mágica es "normal". Algunos autores toman cuadrado mágico para significar cuadrado mágico normal.
Se dice que la plaza mágica es "normal". Algunos autores toman cuadrado mágico para significar cuadrado mágico normal.
Los cuadrados mágicos que incluyen entradas repetidas no se incluyen en esta definición y se denominan 'triviales'. Algunos ejemplos bien conocidos, como el cuadrado mágico de la Sagrada Familia y la plaza de Parker, son triviales en este sentido. Cuando todas las filas y columnas, pero no ambas diagonales, suman la constante mágica, se obtiene un cuadrado semimágico (a veces llamado cuadrado ortomágico).
El estudio matemático de los cuadrados mágicos generalmente se ocupa de su construcción, clasificación y enumeración. Aunque no existen métodos completamente generales para producir todos los cuadrados mágicos de todos los órdenes, históricamente se han descubierto tres técnicas generales: mediante el método de bordes, haciendo cuadrados mágicos compuestos y agregando dos cuadrados preliminares. También hay estrategias más específicas como el método de enumeración continua que reproduce patrones específicos. Los cuadrados mágicos generalmente se clasifican según su orden n como: impar si n es impar, uniformemente par (también conocido como "doblemente par") si n es un múltiplo de 4, imparmente par (también conocido como "simplemente par") si n es cualquier otro número par. Esta clasificación se basa en diferentes técnicas necesarias para construir cuadrados impares, uniformemente pares e imparmente pares. Además de esto, dependiendo de otras propiedades, los cuadrados mágicos también se clasifican como cuadrados mágicos asociativos, cuadrados mágicos pandiagonales, cuadrados mágicos más perfectos, etc. Más desafiante aún, también se han hecho intentos para clasificar todos los cuadrados mágicos de un orden dado como transformaciones de un conjunto más pequeño de cuadrados. Excepto por n ≤ 5, la enumeración de cuadrados mágicos de orden superior sigue siendo un desafío abierto. La enumeración de los cuadrados mágicos más perfectos de cualquier orden solo se logró a fines del siglo XX.
Los cuadrados mágicos tienen una larga historia, que se remonta al menos al año 190 a. C. en China. En varias ocasiones han adquirido un significado oculto o mítico y han aparecido como símbolos en obras de arte. En los tiempos modernos, se han generalizado de varias maneras, incluido el uso de restricciones adicionales o diferentes, la multiplicación en lugar de sumar celdas, el uso de formas alternativas o más de dos dimensiones y la sustitución de números con formas y la suma con operaciones geométricas.

Dürer's
Melancholia I (1514) incluye un pedido 4 cuadrado con suma mágica 34
Historia

Placa de hierro con un cuadrado mágico orden-6 en números arábigos orientales de China, que data de la dinastía Yuan (1271–1368).
El cuadrado mágico de tercer orden era conocido por los matemáticos chinos ya en el año 190 a. C. y se dio explícitamente en el primer siglo de la era común. La primera instancia fechable del cuadrado mágico de cuarto orden ocurrió en 587 EC en India. Especímenes de cuadrados mágicos de orden 3 a 9 aparecen en una enciclopedia de Bagdad c. 983, el Enciclopedia de los Hermanos de la Pureza (Rasa'il Ikhwan al-Safa). A fines del siglo XII, los métodos generales para construir cuadrados mágicos estaban bien establecidos. Alrededor de este tiempo, algunos de estos cuadrados se usaban cada vez más junto con letras mágicas, como en Shams Al-ma'arif, con fines ocultos. En la India, todos los cuadrados mágicos pandiagonales de cuarto orden fueron enumerados por Narayana en 1356. Los cuadrados mágicos se dieron a conocer en Europa a través de la traducción de fuentes árabes como objetos ocultos durante el Renacimiento, y la teoría general tuvo que redescubrirse independientemente de las teorías anteriores. desarrollos en China, India y Medio Oriente. También son notables las culturas antiguas con tradición matemática y numerológica que no descubrieron los cuadrados mágicos: griegos, babilonios, egipcios y precolombinos americanos.
China

Una página que muestra el cuadrado mágico 9×9 de Cheng Dawei
Suanfa tongzong (1593).
Mientras que en el I Ching aparecen referencias antiguas al patrón de números pares e impares en el cuadrado mágico de 3×3, la primera instancia inequívoca de este cuadrado mágico aparece en el capítulo llamado Mingtang (Salón luminoso) de un libro del siglo I Da Dai Liji (Registro de ritos del anciano Dai), que pretendía describir los antiguos ritos chinos de la dinastía Zhou.
Estos números también aparecen en un texto matemático posiblemente anterior llamado Shushu jiyi (Memorias sobre algunas tradiciones del arte matemático), que se dice que fue escrito en 190 a. Esta es la primera aparición registrada de un cuadrado mágico; y se usaba principalmente para la adivinación y la astrología. El cuadrado mágico de 3×3 se denominó "Nueve salas" por los primeros matemáticos chinos. La identificación del cuadrado mágico de 3×3 con el legendario gráfico de Luoshu solo se hizo en el siglo XII, después de lo cual se lo denominó cuadrado de Luoshu. El tratado chino más antiguo que se conserva que muestra cuadrados mágicos de orden superior a 3 es Xugu zheqi suanfa (Continuación de los métodos matemáticos antiguos para dilucidar lo extraño) de Yang Hui, escrito en 1275. El contenido de Yang Los tratados de Hui se recopilaron de obras más antiguas, tanto nativas como extranjeras; y solo explica la construcción de cuadrados mágicos de tercer y cuarto orden, mientras simplemente transmite los diagramas terminados de cuadrados más grandes. Da un cuadrado mágico de orden 3, dos cuadrados para cada orden de 4 a 8, uno de orden nueve y un cuadrado semimágico de orden 10. También da seis círculos mágicos de diversa complejidad.
| | 2 | 16 | 13 | 3
| | 11 | 5 | 8 | 10
| | 7 | 9 | 12 | 6
| | 14 | 4 | 1 | 15
|
| | 1 | 23 | 16 | 4 | 21
| | 15 | 14 | 7 | 18 | 11
| | 24 | 17 | 13 | 9 | 2
| | 20 | 8 | 19 | 12 | 6
| | 5 | 3 | 10 | 22 | 25
|
| | 13 | 22 | 18 | 27 | 11 | 20
| | 31 | 4 | 36 | 9 | 29 | 2 | | 12 | 21 | 14 | 23 | 16 | 25
| | 30 | 3 | 5 | 32 | 34 | 7 | | 17 | 26 | 10 | 19 | 15 | 24
| | 8 | 35 | 28 | 1 | 6 | 33
|
|
| 46 | 8 | 16 | 20 | 29 | 7 | 49
| | 3 | 40 | 35 | 36 | 18 | 41 | 2
| | 44 | 12 | 33 | 23 | 19 | 38 | 6
| | 28 | 26 | 11 | 25 | 39 | 24 | 22
| | 5 | 37 | 31 | 27 | 17 | 13 | 45
| | 48 | 9 | 15 | 14 | 32 | 10 | 47
| | 1 | 43 | 34 | 30 | 21 | 42 | 4
|
| | 61 | 3 | 2 | 64 | 57 | 7 | 6 | 60
| | 12 | 54 | 55 | 9 | 16 | 50 | 51 | 13
| | 20 | 46 | 47 | 17 | 24 | 42 | 43 | 21
| | 37 | 27 | 26 | 40 | 33 | 31 | 30 | 36
| | 29 | 35 | 34 | 32 | 25 | 39 | 38 | 28
| | 44 | 22 | 23 | 41 | 48 | 18 | 19 | 45
| | 52 | 14 | 15 | 49 | 56 | 10 | 11 | 53
| | 5 | 59 | 58 | 8 | 1 | 63 | 62 | 4
|
| | 31 | 76 | 13 | 36 | 81 | 18 | 29 | 74 | 11
| | 22 | 40 | 58 | 27 | 45 | 63 | 20 | 38 | 56
| | 67 | 4 | 49 | 72 | 9 | 54 | 65 | 2 | 47
| | 30 | 75 | 12 | 32 | 77 | 14 | 34 | 79 | 16
| | 21 | 39 | 57 | 23 | 41 | 59 | 25 | 43 | 61
| | 66 | 3 | 48 | 68 | 5 | 50 | 70 | 7 | 52
| | 35 | 80 | 17 | 28 | 73 | 10 | 33 | 78 | 15
| | 26 | 44 | 62 | 19 | 37 | 55 | 24 | 42 | 60
| | 71 | 8 | 53 | 64 | 1 | 46 | 69 | 6 | 51
|
|
Los cuadrados mágicos anteriores de los órdenes 3 a 9 están tomados del tratado de Yang Hui, en el que el principio Luo Shu es claramente evidente. El cuadrado de orden 5 es un cuadrado mágico bordeado, con un cuadrado central de 3×3 formado según el principio de Luo Shu. El cuadrado de orden 9 es un cuadrado mágico compuesto, en el que los nueve subcuadrados de 3×3 también son mágicos. Después de Yang Hui, los cuadrados mágicos aparecen con frecuencia en las matemáticas chinas, como en Dayan suoyin de Ding Yidong (c. 1300), Suanfa tongzong de Cheng Dawei (1593), Shuduyan de Fang Zhongtong (1661) que contiene círculos mágicos, cubos y esferas, Xinzhai zazu de Zhang Chao (c. 1650), que publicó el primer cuadrado mágico de orden diez de China y, por último, el Binaishanfang ji de Bao Qishou (c. 1880), quien dio varias configuraciones mágicas tridimensionales. Sin embargo, a pesar de ser el primero en descubrir los cuadrados mágicos y tener una ventaja de varios siglos, el desarrollo chino de los cuadrados mágicos es muy inferior en comparación con los desarrollos de India, Medio Oriente o Europa. El punto culminante de las matemáticas chinas que se ocupan de los cuadrados mágicos parece estar contenido en la obra de Yang Hui; pero incluso como una colección de métodos más antiguos, este trabajo es mucho más primitivo, careciendo de métodos generales para construir cuadrados mágicos de cualquier orden, en comparación con una colección similar escrita en la misma época por el erudito bizantino Manuel Moschopoulos. Esto posiblemente se deba a que los eruditos chinos & # 39; embelesamiento con el principio Lo Shu, que intentaron adaptar para resolver cuadrados superiores; y después de Yang Hui y la caída de la dinastía Yuan, su purga sistemática de las influencias extranjeras en las matemáticas chinas.
Japón
Japón y China tienen tradiciones matemáticas similares y se han influenciado repetidamente en la historia de los cuadrados mágicos. El interés de los japoneses por los cuadrados mágicos comenzó después de la difusión de las obras chinas, Suanfa de Yang Hui y Suanfa tongzong de Cheng Dawei, en el siglo XVII. y como resultado, casi todos los wasans dedicaron su tiempo a su estudio.
En la edición de 1660 de Ketsugi-sho, Isomura Kittoku proporcionó cuadrados mágicos con bordes ordenados pares e impares, así como círculos mágicos; mientras que la edición de 1684 del mismo libro contenía una gran sección sobre cuadrados mágicos, lo que demuestra que tenía un método general para construir cuadrados mágicos bordeados. En Jinko-ki (1665) de Muramatsu Kudayu Mosei, se muestran tanto cuadrados como círculos mágicos. La construcción cuadrada más grande de Mosei es del orden 19. Nozawa Teicho también publicó varios cuadrados y círculos mágicos en Dokai-sho (1666), Sato Seiko en Kongenki (1666) y Hosino Sanenobu en Ko -ko-gen Sho (1673). Uno de los Siete libros de Seki Takakazu (Hojin Yensan) (1683) está dedicado por completo a los cuadrados y círculos mágicos. Este es el primer libro japonés que brinda un tratamiento general de los cuadrados mágicos en el que se describen claramente los algoritmos para construir cuadrados mágicos con bordes impares, pares simples y pares dobles. En 1694 y 1695, Yueki Ando proporcionó diferentes métodos para crear los cuadrados mágicos y mostró cuadrados de orden 3 a 30. Yoshizane Tanaka (1651–1719) construyó un cubo mágico de cuarto orden en Rakusho-kikan (1683). El estudio de los cuadrados mágicos fue continuado por los alumnos de Seki, en particular por Katahiro Takebe, cuyos cuadrados se muestran en el cuarto volumen de Ichigen Kappo de Shukei Irie, Yoshisuke Matsunaga en Hojin- Shin-jutsu, Yoshihiro Kurushima en Kyushi Iko quien redescubrió un método para producir los cuadrados impares propuestos por Agrippa y Naonobu Ajima. Así, a principios del siglo XVIII, los matemáticos japoneses estaban en posesión de métodos para construir cuadrados mágicos de orden arbitrario. Después de esto, Nushizumi Yamaji inició intentos de enumerar los cuadrados mágicos.
India

El cuadrado mágico 3×3 en diferentes orientaciones formando un cuadrado mágico no normal 6×6, de un manuscrito indio no identificado del siglo XIX.
El cuadrado mágico de 3×3 aparece por primera vez en India en Gargasamhita de Garga, quien recomienda su uso para pacificar los nueve planetas (navagraha). La versión más antigua de este texto data del año 100 EC, pero el pasaje sobre los planetas no pudo haber sido escrito antes del año 400 EC. La primera instancia fechable de un cuadrado mágico de 3 × 3 en India ocurre en un texto médico Siddhayog (c. 900 EC) de Vrnda, que se prescribió a las mujeres en trabajo de parto para facilitar el parto.
El cuadrado mágico fechable de cuarto orden más antiguo del mundo se encuentra en una obra enciclopédica escrita por Varahamihira alrededor del año 587 EC llamada Brhat Samhita. El cuadrado mágico se construye con el propósito de hacer perfumes utilizando 4 sustancias seleccionadas de 16 sustancias diferentes. Cada celda del cuadrado representa un ingrediente en particular, mientras que el número en la celda representa la proporción del ingrediente asociado, de modo que la mezcla de cualquier combinación de cuatro ingredientes a lo largo de las columnas, filas, diagonales, etc., da el volumen total de la mezcla sea 18. Aunque el libro trata principalmente sobre adivinación, el cuadrado mágico se da como una cuestión de diseño combinatorio y no se le atribuyen propiedades mágicas. Las características especiales de este cuadrado mágico fueron comentadas por Bhattotpala (c. 966 CE)
| | 10 | 3 | 13 | 8
| | 5 | 16 | 2 | 11
| | 4 | 9 | 7 | 14
| | 15 | 6 | 12 | 1
|
|
El cuadrado de Varahamihira como se indica arriba tiene una suma de 18. Aquí los números del 1 al 8 aparecen dos veces en el cuadrado. Es un cuadrado mágico pan-diagonal. Se pueden obtener cuatro cuadrados mágicos diferentes sumando 8 a uno de los dos conjuntos de secuencias de 1 a 8. La secuencia se selecciona de manera que el número 8 se agregue exactamente dos veces en cada fila, cada columna y cada una de las diagonales principales. Uno de los posibles cuadrados mágicos que se muestran en el lado derecho. Este cuadrado mágico es notable porque es una rotación de 90 grados de un cuadrado mágico que aparece en el mundo islámico del siglo XIII como uno de los cuadrados mágicos más populares.
La construcción del cuadrado mágico de cuarto orden se detalla en una obra titulada Kaksaputa, compuesta por el alquimista Nagarjuna alrededor del siglo X EC. Todos los cuadrados dados por Nagarjuna son cuadrados mágicos de 4×4, y uno de ellos se llama Nagarjuniya en su honor. Nagarjuna dio un método para construir un cuadrado mágico de 4 × 4 usando un cuadrado esqueleto primario, dada una suma mágica par o impar. El cuadrado de Nagarjuniya se muestra a continuación y tiene una suma total de 100.
| 30 | 16 | 18 | 36
| | 10 | 44 | 22 | 24
| | 32 | 14 | 20 | 34
| | 28 | 26 | 40 | 6
|
| |
El cuadrado de Nagarjuniya es un cuadrado mágico pandiagonal. El cuadrado de Nagarjuniya está formado por dos progresiones aritméticas que parten de 6 y 16 con ocho términos cada una, con una diferencia común entre los términos sucesivos de 4. Cuando estas dos progresiones se reducen a la progresión normal de 1 a 8, se obtiene el cuadrado adyacente.
Alrededor del siglo XII, se inscribió un cuadrado mágico de 4×4 en la pared del templo de Parshvanath en Khajuraho, India. Varios himnos jainistas enseñan cómo hacer cuadrados mágicos, aunque no se pueden fechar.
Hasta donde se sabe, el primer estudio sistemático de los cuadrados mágicos en la India fue realizado por Thakkar Pheru, un erudito jainista, en su Ganitasara Kaumudi (c. 1315). Esta obra contiene una pequeña sección sobre cuadrados mágicos que consta de nueve versos. Aquí da un cuadrado de orden cuatro y alude a su reordenamiento; clasifica los cuadrados mágicos en tres (impares, pares pares y pares impares) según su orden; da un cuadrado de orden seis; y prescribe un método para construir cuadrados pares e impares. Para los cuadrados pares, Pheru divide el cuadrado en cuadrados componentes de orden cuatro y coloca los números en celdas de acuerdo con el patrón de un cuadrado estándar de orden cuatro. Para casillas impares, Pheru da el método usando movimiento de caballo o movimiento de caballero. Aunque algorítmicamente diferente, da el mismo cuadrado que el método de De la Loubere.
El siguiente trabajo completo sobre cuadrados mágicos fue retomado por Narayana Pandit, quien en el capítulo catorce de su Ganita Kaumudi (1356) da métodos generales para su construcción, junto con los principios que rigen dichas construcciones.. Consta de 55 versos de reglas y 17 versos de ejemplos. Narayana da un método para construir todos los cuadrados pan-mágicos de cuarto orden usando el movimiento del caballero; enumera el número de cuadrados mágicos pandiagonales de orden cuatro, 384, incluidas todas las variaciones realizadas por rotación y reflexión; tres métodos generales para cuadrados de cualquier orden y suma constante cuando se conoce un cuadrado estándar del mismo orden; dos métodos, cada uno para construir pares pares, pares impares y de cuadrados cuando se da la suma. Si bien Narayana describe un método más antiguo para cada especie de cuadrado, afirma que el método de superposición para cuadrados uniformemente pares e impares y un método de intercambio para cuadrados imparmente pares es su propia invención. El método de superposición fue redescubierto más tarde por De la Hire en Europa. En la última sección, concibe otras figuras, como círculos, rectángulos y hexágonos, en los que los números pueden disponerse para poseer propiedades similares a las de los cuadrados mágicos. A continuación se muestran algunos de los cuadrados mágicos construidos por Narayana:
| | 1 | 14 | 4 | 15
| | 8 | 11 | 5 | 10
| | 13 | 2 | 16 | 3
| | 12 | 7 | 9 | 6
|
| | 16 | 14 | 7 | 30 | 23
| | 24 | 17 | 10 | 8 | 31
| | 32 | 25 | 18 | 11 | 4
| | 5 | 28 | 26 | 19 | 12
| | 13 | 6 | 29 | 22 | 20
|
| | 1 | 35 | 4 | 33 | 32 | 6
| | 25 | 11 | 9 | 28 | 8 | 30
| | 24 | 14 | 18 | 16 | 17 | 22
| | 13 | 23 | 19 | 21 | 20 | 15
| | 12 | 26 | 27 | 10 | 29 | 7
| | 36 | 2 | 34 | 3 | 5 | 31
|
| | 35 | 26 | 17 | 1 | 62 | 53 | 44
| | 46 | 37 | 21 | 12 | 3 | 64 | 55
| | 57 | 41 | 32 | 23 | 14 | 5 | 66
| | 61 | 52 | 43 | 34 | 25 | 16 | 7
| | 2 | 63 | 54 | 45 | 36 | 27 | 11
| | 13 | 4 | 65 | 56 | 47 | 31 | 22
| | 24 | 15 | 6 | 67 | 51 | 42 | 33
|
| | 60 | 53 | 44 | 37 | 4 | 13 | 20 | 29
| | 3 | 14 | 19 | 30 | 59 | 54 | 43 | 38
| | 58 | 55 | 42 | 39 | 2 | 15 | 18 | 31
| | 1 | 16 | 17 | 32 | 57 | 56 | 41 | 40
| | 61 | 52 | 45 | 36 | 5 | 12 | 21 | 28
| | 6 | 11 | 22 | 27 | 62 | 51 | 46 | 35
| | 63 | 50 | 47 | 34 | 7 | 10 | 23 | 26
| | 8 | 9 | 24 | 25 | 64 | 49 | 48 | 33
|
|
El cuadrado de orden 8 es interesante en sí mismo, ya que es un ejemplo del cuadrado mágico más perfecto. Por cierto, Narayana afirma que el propósito de estudiar cuadrados mágicos es construir yantra, destruir el ego de los malos matemáticos y para el placer de los buenos matemáticos. El tema de los cuadrados mágicos se conoce como bhadraganita y Narayana afirma que el dios Shiva se lo enseñó por primera vez a los hombres.
Oriente Medio, África del Norte, Península Ibérica musulmana

Un cuadrado mágico de 6×6
Libro de las Maravillas (de manuscrito del siglo XVI).
Aunque se desconoce la historia temprana de los cuadrados mágicos en Persia y Arabia, se ha sugerido que se conocían en tiempos preislámicos. Sin embargo, está claro que el estudio de los cuadrados mágicos era común en el Islam medieval y se pensaba que comenzó después de la introducción del ajedrez en la región. La primera aparición fechable de un cuadrado mágico de orden 3 ocurre en Jābir ibn Hayyān's (fl. c. 721 - c. 815) Kitab al-mawazin al-Saghir (El Libro Pequeño de Saldos) donde el cuadrado mágico y su numerología relacionada se asocia con la alquimia. Si bien se sabe que los tratados sobre cuadrados mágicos se escribieron en el siglo IX, los primeros tratados existentes datan del siglo X: uno de Abu'l-Wafa al-Buzjani (c. 998) y otro de Ali b. Ahmad al-Antaki (c. 987). Estos primeros tratados eran puramente matemáticos, y la designación árabe utilizada para los cuadrados mágicos es wafq al-a'dad, que se traduce como disposición armoniosa de los números. A fines del siglo X, los dos tratados de Buzjani y Antaki dejan en claro que los matemáticos del Medio Oriente habían entendido cómo construir cuadrados bordeados de cualquier orden, así como cuadrados mágicos simples de órdenes pequeños (n ≤ 6) que se usaron para hacer cuadrados mágicos compuestos. Una muestra de cuadrados mágicos de los órdenes 3 a 9 ideados por matemáticos del Medio Oriente aparece en una enciclopedia de Bagdad c. 983, Rasa'il Ikhwan al-Safa (la Enciclopedia de los Hermanos de la Pureza). Los cuadrados de orden 3 a 7 de Rasa'il se dan a continuación:
| | 4 | 14 | 15 | 1
| | 9 | 7 | 6 | 12
| | 5 | 11 | 10 | 8
| | 16 | 2 | 3 | 13
|
| | 21 | 3 | 4 | 12 | 25
| | 15 | 17 | 6 | 19 | 8
| | 10 | 24 | 13 | 2 | 16
| | 18 | 7 | 20 | 9 | 11
| | 1 | 14 | 22 | 23 | 5
|
| | 11 | 22 | 32 | 5 | 23 | 18
| | 25 | 16 | 7 | 30 | 13 | 20
| | 27 | 6 | 35 | 36 | 4 | 3
| | 10 | 31 | 1 | 2 | 33 | 34
| | 14 | 19 | 8 | 29 | 26 | 15
| | 24 | 17 | 28 | 9 | 12 | 21
|
| | 47 | 11 | 8 | 9 | 6 | 45 | 49
| | 4 | 37 | 20 | 17 | 16 | 35 | 46
| | 2 | 18 | 26 | 21 | 28 | 32 | 48
| | 43 | 19 | 27 | 25 | 23 | 31 | 7
| | 38 | 36 | 22 | 29 | 24 | 14 | 12
| | 40 | 15 | 30 | 33 | 34 | 13 | 10
| | 1 | 39 | 42 | 41 | 44 | 5 | 3
|
|
El siglo XI vio el descubrimiento de varias formas de construir cuadrados mágicos simples para órdenes pares e impares; el caso más difícil de caso par-impar (n = 4k + 2) fue resuelto por Ibn al-Haytham con k par (c. 1040), y completamente por el principios del siglo XII, si no ya en la segunda mitad del siglo XI. Casi al mismo tiempo, se estaban construyendo plazas pandiagonales. Los tratados sobre cuadrados mágicos fueron numerosos en los siglos XI y XII. Estos desarrollos posteriores tendieron a ser mejoras o simplificaciones de los métodos existentes. Desde el siglo XIII en adelante, los cuadrados mágicos se destinaron cada vez más a fines ocultos. Sin embargo, muchos de estos textos posteriores escritos con fines ocultos simplemente representan ciertos cuadrados mágicos y mencionan sus atributos, sin describir su principio de construcción, y solo algunos autores mantienen viva la teoría general. Uno de esos ocultistas fue el argelino Ahmad al-Buni (c. 1225), quien dio métodos generales para construir cuadrados mágicos bordeados; algunos otros fueron el Shabramallisi egipcio del siglo XVII y el al-Kishnawi nigeriano del siglo XVIII.
El cuadrado mágico de orden tres se describió como un amuleto para tener hijos desde sus primeras apariciones literarias en las obras alquímicas de Jābir ibn Hayyān (fl. c. 721 – c. 815) y al-Ghazālī (1058–1111) y se conservó en la tradición de las tablas planetarias. La aparición más temprana de la asociación de siete cuadrados mágicos con las virtudes de los siete cuerpos celestes aparece en el erudito andaluz Ibn Zarkali's (conocido como Azarquiel en Europa) (1029–1087) Kitāb tadbīrāt al-kawākib (Libro sobre las Influencias de los Planetas). Un siglo más tarde, el erudito argelino Ahmad al-Buni atribuyó propiedades místicas a los cuadrados mágicos en su influyente libro Shams al-Ma'arif (El Libro del Sol de la Gnosis y el Sutilezas de las cosas elevadas), que también describe su construcción. Esta tradición sobre una serie de cuadrados mágicos de orden tres a nueve, que están asociados con los siete planetas, sobrevive en versiones griegas, árabes y latinas. También hay referencias al uso de cuadrados mágicos en los cálculos astrológicos, práctica que parece tener su origen en los árabes.
Europa Latina

Esta página de Athanasius Kircher's
Oedipus Aegyptiacus (1653) pertenece a un tratado en cuadrados mágicos y muestra los
Sigillum Iovis asociado con Júpiter
A diferencia de Persia y Arabia, existe mejor documentación sobre cómo se transmitieron los cuadrados mágicos a Europa. Alrededor de 1315, influenciado por fuentes árabes, el erudito bizantino griego Manuel Moschopoulos escribió un tratado matemático sobre el tema de los cuadrados mágicos, dejando de lado el misticismo de sus predecesores del Medio Oriente, donde dio dos métodos para cuadrados impares y dos métodos para cuadrados pares.. Moschopoulos fue esencialmente desconocido para la Europa latina hasta finales del siglo XVII, cuando Philippe de la Hire redescubrió su tratado en la Biblioteca Real de París. Sin embargo, no fue el primer europeo que escribió sobre cuadrados mágicos; y los cuadrados mágicos se difundieron al resto de Europa a través de España e Italia como objetos ocultos. Los primeros tratados ocultos que mostraban los cuadrados no describían cómo se construían. Por lo tanto, toda la teoría tuvo que ser redescubierta.
Los cuadrados mágicos habían aparecido por primera vez en Europa en Kitāb tadbīrāt al-kawākib (Libro de las Influencias de los Planetas) escrito por Ibn Zarkali de Toledo, Al-Andalus, como cuadrados planetarios en el siglo XI. El cuadrado mágico de tres fue discutido de manera numerológica a principios del siglo XII por el erudito judío Abraham ibn Ezra de Toledo, lo que influyó en los cabalistas posteriores. La obra de Ibn Zarkali fue traducida como Libro de Astromagia en la década de 1280, debido a Alfonso X de Castilla. En el texto alfonsino se asignan cuadrados mágicos de diferente orden a los respectivos planetas, como en la literatura islámica; desafortunadamente, de todos los cuadrados discutidos, el cuadrado mágico de Marte de orden cinco es el único cuadrado exhibido en el manuscrito.
Los cuadrados mágicos vuelven a aparecer en Florencia, Italia, en el siglo XIV. Un cuadrado de 6×6 y un cuadrado de 9×9 se exhiben en un manuscrito del Trattato d'Abbaco (Tratado del Ábaco) de Paolo Dagomari. Es interesante observar que Paolo Dagomari, como Pacioli después de él, se refiere a los cuadrados como una base útil para inventar preguntas y juegos matemáticos, y no menciona ningún uso mágico. Sin embargo, dicho sea de paso, también se refiere a ellos como los cuadrados del Sol y la Luna, respectivamente, y menciona que entran en cálculos astrológicos que no están mejor especificados. Como se ha dicho, el mismo punto de vista parece motivar al compatriota florentino Luca Pacioli, que describe cuadrados de 3×3 a 9×9 en su obra De Viribus Quantitatis a finales del siglo XV.
Europa después del siglo XV

Una página de Simon de la Loubère
Du Royaume de Siam (1691) mostrando el método indio de construir una extraña plaza mágica.
Los cuadrados planetarios se habían diseminado en el norte de Europa a finales del siglo XV. Por ejemplo, el manuscrito de Cracovia de Picatrix de Polonia muestra cuadrados mágicos de órdenes 3 a 9. El mismo conjunto de cuadrados que en el manuscrito de Cracovia aparece más tarde en los escritos de Paracelso en Archidoxa Magica (1567), aunque en forma muy confusa. En 1514 Albrecht Dürer inmortalizó un cuadrado de 4×4 en su famoso grabado Melencolia I. Paracelsus' el contemporáneo Heinrich Cornelius Agrippa von Nettesheim publicó su famoso libro de tres volúmenes De occulta philosophia en 1531, donde dedicó el Capítulo 22 del Libro II a los cuadrados planetarios que se muestran a continuación. El mismo conjunto de cuadrados dado por Agrippa reaparece en 1539 en Practica Arithmetice de Girolamo Cardano, donde explica la construcción de los cuadrados impares utilizando el "método del diamante", que luego fue reproducido por Bachet. La tradición de los cuadrados planetarios fue continuada en el siglo XVII por Athanasius Kircher en Oedipi Aegyptici (1653). En Alemania, los tratados matemáticos sobre cuadrados mágicos fueron escritos en 1544 por Michael Stifel en Arithmetica Integra, quien redescubrió los cuadrados bordeados, y Adam Riese, quien redescubrió el método de numeración continua para construir cuadrados ordenados impares publicado por Agrippa. Sin embargo, debido a las convulsiones religiosas de la época, estas obras fueron desconocidas para el resto de Europa.
| Júpiter=34
| 4 | 14 | 15 | 1
| | 9 | 7 | 6 | 12
| | 5 | 11 | 10 | 8
| | 16 | 2 | 3 | 13
| | Mars=65
| 11 | 24 | 7 | 20 | 3
| | 4 | 12 | 25 | 8 | 16
| | 17 | 5 | 13 | 21 | 9
| | 10 | 18 | 1 | 14 | 22
| | 23 | 6 | 19 | 2 | 15
| | Sol=111
| 6 | 32 | 3 | 34 | 35 | 1
| | 7 | 11 | 27 | 28 | 8 | 30
| | 19 | 14 | 16 | 15 | 23 | 24
| | 18 | 20 | 22 | 21 | 17 | 13
| | 25 | 29 | 10 | 9 | 26 | 12
| | 36 | 5 | 33 | 4 | 2 | 31
| |
Venus=175
| 22 | 47 | 16 | 41 | 10 | 35 | 4
| | 5 | 23 | 48 | 17 | 42 | 11 | 29
| | 30 | 6 | 24 | 49 | 18 | 36 | 12
| | 13 | 31 | 7 | 25 | 43 | 19 | 37
| | 38 | 14 | 32 | 1 | 26 | 44 | 20
| | 21 | 39 | 8 | 33 | 2 | 27 | 45
| | 46 | 15 | 40 | 9 | 34 | 3 | 28
| | Mercurio=260
| 8 | 58 | 59 | 5 | 4 | 62 | 63 | 1
| | 49 | 15 | 14 | 52 | 53 | 11 | 10 | 56
| | 41 | 23 | 22 | 44 | 45 | 19 | 18 | 48
| | 32 | 34 | 35 | 29 | 28 | 38 | 39 | 25
| | 40 | 26 | 27 | 37 | 36 | 30 | 31 | 33
| | 17 | 47 | 46 | 20 | 21 | 43 | 42 | 24
| | 9 | 55 | 54 | 12 | 13 | 51 | 50 | 16
| | 64 | 2 | 3 | 61 | 60 | 6 | 7 | 57
| | Luna=369
| 37 | 78 | 29 | 70 | 21 | 62 | 13 | 54 | 5
| | 6 | 38 | 79 | 30 | 71 | 22 | 63 | 14 | 46
| | 47 | 7 | 39 | 80 | 31 | 72 | 23 | 55 | 15
| | 16 | 48 | 8 | 40 | 81 | 32 | 64 | 24 | 56
| | 57 | 17 | 49 | 9 | 41 | 73 | 33 | 65 | 25
| | 26 | 58 | 18 | 50 | 1 | 42 | 74 | 34 | 66
| | 67 | 27 | 59 | 10 | 51 | 2 | 43 | 75 | 35
| | 36 | 68 | 19 | 60 | 11 | 52 | 3 | 44 | 76
| | 77 | 28 | 69 | 20 | 61 | 12 | 53 | 4 | 45
| |
En 1624, Francia, Claude Gaspard Bachet describió el "método del diamante" por construir los cuadrados ordenados impares de Agrippa en su libro Problèmes Plaisants. Durante 1640 Bernard Frenicle de Bessy y Pierre Fermat intercambiaron cartas sobre cuadrados y cubos mágicos, y en una de las cartas Fermat se jacta de poder construir 1.004.144.995.344 cuadrados mágicos de orden 8 por su método. Antoine Arnauld da un relato temprano sobre la construcción de plazas bordeadas en sus Nouveaux éléments de géométrie (1667). En los dos tratados Des quarrez ou tables magiques y Table générale des quarrez magiques de quatre de côté, publicados póstumamente en 1693, veinte años después de su muerte, Bernard Frenicle de Bessy demostró que había exactamente 880 cuadrados mágicos distintos de orden cuatro. Frenicle proporcionó métodos para construir cuadrados mágicos de cualquier orden par e impar, donde los cuadrados ordenados pares se construyeron usando bordes. También demostró que el intercambio de filas y columnas de un cuadrado mágico producía nuevos cuadrados mágicos. En 1691, Simon de la Loubère describió el método indio continuo para construir cuadrados mágicos impares en su libro Du Royaume de Siam, que había aprendido al regresar de una misión diplomática en Siam, que era más rápido que Método de Bachet. En un intento por explicar su funcionamiento, de la Loubere usó los números primarios y los números raíz, y redescubrió el método de sumar dos cuadrados preliminares. Este método fue investigado más a fondo por Abbe Poignard en Traité des quarrés sublimes (1704), por Philippe de La Hire en Mémoires de l'Académie des Sciences para la Royal Academy (1705), y por Joseph Sauveur en Construction des quarrés magiques (1710). Los cuadrados con bordes concéntricos también fueron estudiados por De la Hire en 1705, mientras que Sauveur introdujo cubos mágicos y cuadrados con letras, que Euler retomó más tarde en 1776, a quien a menudo se le atribuye su invención. En 1750, d'Ons-le-Bray redescubrió el método de construir cuadrados doblemente pares y pares simples utilizando la técnica de bordes; mientras que en 1767 Benjamin Franklin publicó un cuadrado semimágico que tenía las propiedades del cuadrado homónimo de Franklin. En ese momento, el misticismo anterior relacionado con los cuadrados mágicos se había desvanecido por completo y el tema se trató como parte de las matemáticas recreativas.
En el siglo XIX, Bernard Violle brindó un tratamiento integral de los cuadrados mágicos en sus tres volúmenes Traité complet des carrés magiques (1837–1838), que también describía cubos mágicos, paralelogramos, paralelepípedos y círculos Los cuadrados pandiagonales fueron estudiados extensamente por Andrew Hollingworth Frost, quien los aprendió mientras estaba en la ciudad de Nasik, India (llamándolos así cuadrados Nasik) en una serie de artículos: En el camino del caballero (1877), Sobre las propiedades generales de los cuadrados de Nasik (1878), Sobre las propiedades generales de los cubos de Nasik (1878), Sobre la construcción de los cuadrados de Nasik cualquier orden (1896). Demostró que es imposible tener cuadrados mágicos simples pandiagonales normales. Frederick AP Barnard construyó cuadrados mágicos con incrustaciones y otras figuras mágicas tridimensionales como esferas mágicas y cilindros mágicos en Teoría de los cuadrados mágicos y de los cubos mágicos (1888). En 1897, Emroy McClintock publicó On the most perfect form of magic squares, acuñando las palabras pandiagonal square y most perfect square, que anteriormente habían sido referido como perfecto, o diabólico, o Nasik.
Algunos cuadrados mágicos famosos

Lo Shu de "El Fenómeno Astronómico"
Tien Yuan Fa Wei). Compilado por Bao Yunlong en el siglo XIII, publicado durante la dinastía Ming, 1457-1463.
Cuadrado mágico Luo Shu
Las leyendas que datan del año 650 a. C. cuentan la historia de Lo Shu (洛書) o "pergamino del río Lo". Según la leyenda, hubo una vez en la antigua China una gran inundación. Mientras el gran rey Yu intentaba canalizar el agua hacia el mar, una tortuga emergió con un curioso patrón en su caparazón: una cuadrícula de 3×3 en la que se disponían puntos circulares de números, de modo que la suma de los números en cada fila, columna y diagonal era la misma: 15. Según la leyenda, a partir de entonces la gente pudo usar este patrón de cierta manera para controlar el río y protegerse de las inundaciones. El Cuadrado Lo Shu, como se llama el cuadrado mágico en el caparazón de la tortuga, es el único cuadrado mágico normal de orden tres en el que el 1 está en la parte inferior y el 2 en la esquina superior derecha. Cada cuadrado mágico normal de orden tres se obtiene del Lo Shu por rotación o reflexión.
Cuadrado mágico en el templo de Parshavnath

Plaza Mágica en el templo Parshvanatha, en Khajuraho, India
Hay un conocido cuadrado mágico normal de 4×4 del siglo XII inscrito en la pared del templo Parshvanath en Khajuraho, India.
| 7 | 12 | 1 | 14
|
| 2 | 13 | 8 | 11
|
| 16 | 3 | 10 | 5
|
| 9 | 6 | 15 | 4
|
Esto se conoce como Chautisa Yantra (Chautisa, 34; Yantra, lit. "dispositivo"), ya que su suma mágica es 34. Es uno de los tres cuadrados mágicos pandiagonales de 4×4 y también es una instancia del cuadrado mágico más perfecto. El estudio de este cuadrado condujo a la apreciación de los cuadrados pandiagonales por parte de los matemáticos europeos a fines del siglo XIX. Los cuadrados pandiagonales se denominaban cuadrados Nasik o cuadrados Jain en la literatura inglesa más antigua.
Cuadrado mágico de Alberto Durero
Se cree que el cuadrado mágico normal de orden cuatro que Albrecht Dürer inmortalizó en su grabado de 1514 Melencolia I, mencionado anteriormente, es el primero que se ve en el arte europeo. La cuadratura asociada a Júpiter aparece como un talismán utilizado para ahuyentar la melancolía. Es muy similar a la plaza de Yang Hui, que fue creada en China unos 250 años antes de la época de Durero. Como con todo cuadrado mágico normal de orden 4, la suma mágica es 34. Pero en el cuadrado de Durer también se encuentra esta suma
en cada uno de los cuadrantes, en los cuatro cuadrados del centro, y en los cuadrados de las esquinas (tanto de las cuadrículas de 4×4 como de las cuatro contenidas de 3×3). Esta suma también se puede encontrar en los cuatro números exteriores en el sentido de las agujas del reloj desde las esquinas (3+8+14+9) y también en los cuatro en el sentido contrario a las agujas del reloj (las ubicaciones de las cuatro reinas en las dos soluciones del rompecabezas de las 4 reinas), los dos conjuntos de cuatro números simétricos (2+8+9+15 y 3+5+12+14), la suma de las dos entradas centrales de las dos columnas y filas exteriores (5+9+8+12 y 3+2+ 15+14), y en cuatro cuartetos en forma de cometa o cruz (3+5+11+15, 2+10+8+14, 3+9+7+15 y 2+6+12+14). Los dos números en el medio de la fila inferior dan la fecha del grabado: 1514. Los números 1 y 4 a cada lado de la fecha corresponden respectivamente a las letras "A" y "D," que son las iniciales del artista.
| 16 | 3 | 2 | 13
|
| 5 | 10 | 11 | 8
|
| 9 | 6 | 7 | 12
|
| 4 | 15 | 14 | 1
|
El cuadrado mágico de Durero también se puede extender a un cubo mágico.
Cuadrado mágico Sagrada Familia

Una plaza mágica en la fachada de la iglesia de la Sagrada Familia
La fachada de la Pasión de la iglesia de la Sagrada Familia de Barcelona, conceptualizada por Antoni Gaudí y diseñada por el escultor Josep Subirachs, presenta un cuadrado mágico trivial de orden 4: La constante mágica del cuadrado es 33, la edad de Jesús en el momento de la pasión. Estructuralmente, es muy similar al cuadrado mágico de Melancholia, pero se han reducido los números en cuatro de las celdas en 1.
| 1 | 14 | 14 | 4
|
| 11 | 7 | 6 | 9
|
| 8 | 10 | 10 | 5
|
| 13 | 2 | 3 | 15
|
Los cuadrados triviales como este generalmente no son matemáticamente interesantes y solo tienen un significado histórico. Lee Sallows ha señalado que, debido a la ignorancia de Subirachs sobre la teoría del cuadrado mágico, el renombrado escultor cometió un error innecesario y apoya esta afirmación dando varios ejemplos de cuadrados mágicos 4×4 no triviales que muestran la constante mágica deseada. de 33
Al igual que el cuadrado mágico de Durero, el cuadrado mágico de la Sagrada Familia también se puede extender a un cubo mágico.
Plaza Parker
El Parker Square, llamado así por el matemático recreativo Matt Parker, es un intento de crear un 3 × 3 cuadrados mágicos de cuadrados: un preciado sin resolver problema desde Euler. Parker Square es un cuadrado semimágico trivial ya que usa algunos números más de una vez, y la diagonal 232 + 372 + 472 suma a 4107, no 3051 como para todas las demás filas, columnas o diagonales. Parker Square se convirtió en una 'mascota para las personas que lo intentan, pero al final se quedan cortas'. También es una metáfora de algo que está casi bien, pero está un poco fuera de lugar.
| 292 | 12 | 472 |
| 412 | 372 | 12 |
| 232 | 412 | 292 |
Plaza del jardinero
La Plaza Gardner, llamada así por el matemático recreativo Martin Gardner, similar a la Plaza Parker,
se da como problema determinar a, b, c y d;
Esta solución para a=74, b=113, c=94 yd=97 da un cuadrado semimágico; la diagonal 1272 + b2 + d2 suma 38307, no 21609 en cuanto a todos los demás filas, columnas y diagonales;
| 1272 | 462 | 582 | 21609
|
| 22 | 1132 | 942 | 21609
|
| 742 | 822 | 972 | 21609
|
| 21609 | 21609 | 21609 | 38307
|
Propiedades de los cuadrados mágicos
Constante mágica
La constante que es la suma de cualquier fila, o columna, o diagonal se llama la constante mágica o suma mágica, M. Cada cuadrado mágico normal tiene una constante dependencia del orden n, calculado por la fórmula M=n()n2+1)/2{displaystyle M=n(n^{2}+1)/2} . Esto puede demostrarse notando que la suma de 1,2,...,n2{displaystyle 1,2,...,n^{2}
. Esto puede demostrarse notando que la suma de 1,2,...,n2{displaystyle 1,2,...,n^{2} es n2()n2+1)/2{displaystyle n^{2}(n^{2}+1)/2}
es n2()n2+1)/2{displaystyle n^{2}(n^{2}+1)/2} . Puesto que la suma de cada fila es M{displaystyle M}
. Puesto que la suma de cada fila es M{displaystyle M} , la suma de n{displaystyle n}
, la suma de n{displaystyle n} filas es nM=n2()n2+1)/2{displaystyle nM=n^{2}(n^{2}+1)/2}
filas es nM=n2()n2+1)/2{displaystyle nM=n^{2}(n^{2}+1)/2} , que cuando se divide por el orden n cede la constante mágica. Para cuadrados mágicos normales de órdenes n = 3, 4, 5, 6, 7, y 8, las constantes mágicas son, respectivamente: 15, 34, 65, 111, 175 y 260 (secuencia A006003 en el OEIS).
, que cuando se divide por el orden n cede la constante mágica. Para cuadrados mágicos normales de órdenes n = 3, 4, 5, 6, 7, y 8, las constantes mágicas son, respectivamente: 15, 34, 65, 111, 175 y 260 (secuencia A006003 en el OEIS).
El cuadrado mágico de orden 1 es trivial
El cuadrado mágico de 1×1, con una sola celda que contiene el número 1, se llama trivial, porque normalmente no se considera cuando se habla de cuadrados mágicos; pero ciertamente es un cuadrado mágico por definición, si una sola celda es considerada como un cuadrado de orden uno.
El cuadrado mágico de orden 2 no se puede construir
Se pueden construir cuadrados mágicos normales de todos los tamaños excepto 2×2 (es decir, donde el orden n = 2).
Centro de masa
Si los números en el cuadrado mágico se ven como masas ubicadas en varias celdas, entonces el centro de masa de un cuadrado mágico coincide con su centro geométrico.
Momento de inercia
El momento de inercia de un cuadrado mágico se ha definido como la suma sobre todas las celdas del número en los tiempos celulares la distancia cuadrada del centro de la célula al centro de la plaza; aquí la unidad de medición es el ancho de una célula. (Por ejemplo, una célula esquina de un cuadrado 3×3 tiene una distancia 2,{displaystyle {sqrt {2}} una célula de borde no-corner tiene una distancia de 1, y la célula central tiene una distancia de 0.) Entonces todos los cuadrados mágicos de un orden dado tienen el mismo momento de inercia que el uno al otro. Para el caso orden-3 el momento de inercia es siempre 60, mientras que para el caso orden-4 el momento de inercia es siempre 340. En general, para el n×n el momento de la inercia es n2()n4− − 1)/12.{displaystyle n^{2}(n^{4}-1)/12.}
una célula de borde no-corner tiene una distancia de 1, y la célula central tiene una distancia de 0.) Entonces todos los cuadrados mágicos de un orden dado tienen el mismo momento de inercia que el uno al otro. Para el caso orden-3 el momento de inercia es siempre 60, mientras que para el caso orden-4 el momento de inercia es siempre 340. En general, para el n×n el momento de la inercia es n2()n4− − 1)/12.{displaystyle n^{2}(n^{4}-1)/12.}
Descomposición de Birkhoff-von Neumann
Dividir cada número de la plaza mágica por la constante mágica producirá una matriz doblemente estocástica, cuya fila suma y columna suma igual a la unidad. Sin embargo, a diferencia de la doble matriz estocástica, las sumas diagonales de tales matrices también serán iguales a la unidad. Así, tales matrices constituyen un subconjunto de matriz doblemente estocástica. El teorema Birkhoff-von Neumann declara que para cualquier matriz doblemente estocástica A{displaystyle A} , hay números reales Silencio Silencio 1,...... ,Silencio Silencio k≥ ≥ 0{displaystyle theta _{1},ldotstheta ¿Qué? 0}
, hay números reales Silencio Silencio 1,...... ,Silencio Silencio k≥ ≥ 0{displaystyle theta _{1},ldotstheta ¿Qué? 0} , donde .. i=1kSilencio Silencio i=1{displaystyle sum _{i=1}{k}theta ¿Qué?
, donde .. i=1kSilencio Silencio i=1{displaystyle sum _{i=1}{k}theta ¿Qué? y matrices de permutación P1,...... ,Pk{displaystyle P_{1},ldots P_{k}
y matrices de permutación P1,...... ,Pk{displaystyle P_{1},ldots P_{k} tales que
tales que
- A=Silencio Silencio 1P1+⋯ ⋯ +Silencio Silencio kPk.{displaystyle A=theta - ¿Qué? + 'theta - ¿Qué?

Esta representación puede no ser única en general. Por el teorema de Marcus-Ree, sin embargo, no es necesario k≤ ≤ n2− − 2n+2{displaystyle kleq n^{2}-2n+2} términos en cualquier descomposición. Claramente, esta descomposición también lleva a cuadrados mágicos, ya que una plaza mágica se puede recuperar de una matriz doblemente estocástica multiplicando por la constante mágica.
términos en cualquier descomposición. Claramente, esta descomposición también lleva a cuadrados mágicos, ya que una plaza mágica se puede recuperar de una matriz doblemente estocástica multiplicando por la constante mágica.
Clasificación de los cuadrados mágicos

Diagrama Euler de los requisitos de algunos tipos de cuadrados mágicos 4×4. Células del mismo color suma a la constante mágica. En 4×4 plazas mágicas más perfectas, cualquier 2 células que son 2 células diagonalmente separadas (incluyendo envoltura) suma a la mitad de la constante mágica, por lo tanto, cualquier 2 de estos pares también suma a la constante mágica.
Si bien la clasificación de los cuadrados mágicos se puede hacer de muchas maneras, a continuación se brindan algunas categorías útiles. Una matriz cuadrada n×n de números enteros 1, 2,..., n2 se llama:
- Plaza semimagica cuando sus filas y columnas suman para dar la constante mágica.
- Plaza de magia simple cuando sus filas, columnas y dos diagonales suman para dar constante mágico y no más. They are also known as cuadrados mágicos ordinarios o cuadrados mágicos normales.
- Plaza mágica autocomplementaria cuando es un cuadrado mágico que cuando se complementa (es decir, cada número se resta de n2 + 1) dará una versión rota o reflejada de la plaza mágica original.
- Plaza de magia asociativa cuando es un cuadrado mágico con otra propiedad que cada número añadido al número equidistante, en una línea recta, del centro da n2 + 1. También se llaman cuadrados mágicos simétricos. Los cuadrados de magia asociativa no existen para los cuadrados de orden cantable. Todos los cuadrados de magia asociativa son cuadrados mágicos autocomplementarios también.
- Plaza de magia pandiagonal cuando es un cuadrado mágico con otra propiedad que las diagonales rotas suman a la constante mágica. También se llaman cuadrados panmagicos, cuadrados perfectos, cuadrados diabólicos, Jain cuadrados, o Plazas Nasik. Los cuadrados panmagicos no existen para órdenes cantadas. Sin embargo, incluso los cuadrados no normales pueden ser panmagicos.
- Plaza de magia ultra cuando es tanto la plaza de magia asociativa como pandiagonal. Plaza de magia ultra existen sólo para órdenes n ≥ 5.
- Plaza de magia fronteriza cuando es un cuadrado mágico y sigue siendo mágico cuando se eliminan las filas y columnas en el borde exterior. También se llaman concéntricos cuadrados de magia si quitar una frontera de una plaza sucesivamente da otra plaza de magia fronteriza más pequeña. La plaza de magia fronteriza no existe para el orden 4.
- cuadrado mágico compuesto cuando es un cuadrado mágico que es creado por "multiplying" (en algún sentido) cuadrados mágicos más pequeños, tal que el orden de la plaza mágica compuesta es un múltiplo de la orden de los cuadrados más pequeños. Tales cuadrados generalmente se pueden dividir en sub-cuadras mágicas no superpuestas más pequeñas.
- Plaza de magia incrustada cuando es un cuadrado mágico dentro del cual un sub-cuadra mágico está incrustado, independientemente de la técnica de construcción. Los submarinos mágicos incrustados se denominan incrustaciones.
- Plaza de magia más perfecta cuando es un cuadrado mágico pandiagonal con dos propiedades adicionales (i) cada subsquare 2×2 añadir a 1/k de la constante mágica donde n = 4k, y (ii) todos los pares de enteros distantes n/2 a lo largo de cualquier diagonal (major o roto) son complementarios (es decir, suma a n2 + 1). La primera propiedad se denomina compactación, mientras que la segunda propiedad se conoce como integridad. Los cuadrados mágicos más perfectos existen sólo para cuadrados de orden doble. Todas las plazas pandiagonales del orden 4 son también más perfectas.
- cuadrado mágico de Franklin cuando es un cuadrado doblemente incluso mágico con tres propiedades adicionales (i) cada diagonal doblado añade a la constante mágica, (ii) cada media fila y media columna que comienza en un borde exterior añade a la mitad de la constante mágica, y (iii) la plaza es compacto.
- Plaza multimágico cuando es un cuadrado mágico que permanece mágico incluso si todos sus números son reemplazados por su k-a potencia para 1 ≤ k ≤ P. They are also known as P-multimagic square o cuadrados satánicos. They are also referred to as cuadrados bimagicos, cuadrados trimagicos, tetramagic cuadrados, cuadrados pentamagicos cuando el valor de P es 2, 3, 4 y 5 respectivamente.
Enumeración de cuadrados mágicos
Problema no resuelto en matemáticas:
¿Cuántos? n× × n{displaystyle ntimes n} cuadrados mágicos, y cuántos tori mágico de orden n, están allí para 5}" xmlns="http://www.w3.org/1998/Math/MathML">n■5{displaystyle n confianza5}
cuadrados mágicos, y cuántos tori mágico de orden n, están allí para 5}" xmlns="http://www.w3.org/1998/Math/MathML">n■5{displaystyle n confianza5}![]() 5" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/8bd2bf6a3536376e04ca3924122de04b11344796" style="vertical-align: -0.338ex; width:5.656ex; height:2.176ex;"/>?
5" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/8bd2bf6a3536376e04ca3924122de04b11344796" style="vertical-align: -0.338ex; width:5.656ex; height:2.176ex;"/>?
(Problemas más no resueltos en matemáticas)
- Plazas de bajo orden
Solo hay un cuadrado mágico (trivial) de orden 1 y ningún cuadrado mágico de orden 2. Como se mencionó anteriormente, el conjunto de cuadrados normales de orden tres constituye una sola clase de equivalencia, todos equivalentes al cuadrado de Lo Shu. Por lo tanto, básicamente solo hay un cuadrado mágico normal de orden 3.
El número de cuadrados mágicos n × n diferentes para n del 1 al 5, sin contar las rotaciones y los reflejos, es:
- 1, 0, 1, 880, 275305224. (secuencia) A006052 en el OEIS)
Se ha estimado que el número para n = 6 es (1,7745 ± 0,0016) × 1019.
- Tori mágico
Con referencias cruzadas a la secuencia anterior, una nueva clasificación enumera los toros mágicos que muestran estos cuadrados mágicos. El número de toros mágicos de orden n del 1 al 5, es:
- 1, 0, 1, 255, 251449712 (secuencia A270876 en el OEIS).
- Plazas de orden superior y tori
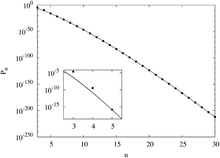
Parcela semi-log de Pn, la probabilidad de cuadrados mágicos de dimensión n
El número de cuadrados mágicos normales distintos aumenta rápidamente para órdenes superiores.
Los 880 cuadrados mágicos de orden 4 se muestran en 255 toros mágicos de orden 4 y los 275 305 224 cuadrados de orden 5 se muestran en 251 449 712 toros mágicos de orden 5. Todavía no se conoce el número de toros mágicos y distintos cuadrados normales. cualquier orden superior.
Los algoritmos tienden a generar solo cuadrados mágicos de cierto tipo o clasificación, lo que dificulta bastante el recuento de todos los cuadrados mágicos posibles. Dado que los métodos de conteo tradicionales no han tenido éxito, se ha aplicado el análisis estadístico utilizando el método de Monte Carlo. El principio básico aplicado a los cuadrados mágicos es generar aleatoriamente matrices n × n de los elementos 1 a n2 y comprobar si el resultado es un cuadrado mágico. La probabilidad de que una matriz de números generada aleatoriamente sea un cuadrado mágico se usa para aproximar el número de cuadrados mágicos.
Versiones más complejas del método de Monte Carlo, como el intercambio de Monte Carlo y el retroceso de Monte Carlo han producido estimaciones aún más precisas. Utilizando estos métodos se ha demostrado que la probabilidad de cuadrados mágicos disminuye rápidamente a medida que n aumenta. El uso de funciones de ajuste da las curvas que se ven a la derecha.
Transformaciones que conservan la propiedad mágica
Para cualquier cuadrado mágico
- La suma de cada dos cuadrados mágicos del mismo orden por adición de matriz es un cuadrado mágico.
- Un cuadrado mágico sigue siendo mágico cuando todos sus números pasan por la misma transformación lineal (es decir, una función de la forma f()x) m x + b). Por ejemplo, un cuadrado mágico sigue siendo mágico cuando sus números se multiplican por cualquier constante. Además, un cuadrado mágico sigue siendo mágico cuando una constante se añade o se resta a sus números, o si sus números se restan de una constante. En particular, si cada elemento en un cuadrado de orden mágico normal n{displaystyle n}
 se restringe de n2+1{displaystyle n^{2}+1}
se restringe de n2+1{displaystyle n^{2}+1} , se obtiene el complemento de la plaza original. En el ejemplo a continuación, cada elemento de la plaza mágica de la izquierda se resta de 17 para obtener el complemento cuadrado mágico a la derecha.
, se obtiene el complemento de la plaza original. En el ejemplo a continuación, cada elemento de la plaza mágica de la izquierda se resta de 17 para obtener el complemento cuadrado mágico a la derecha.
| 10 | 3 | 13 | 8
| | 5 | 16 | 2 | 11
| | 4 | 9 | 7 | 14
| | 15 | 6 | 12 | 1
|
| | 7 | 14 | 4 | 9
| | 12 | 1 | 15 | 6
| | 13 | 8 | 10 | 3
| | 2 | 11 | 5 | 16
|
|
- Un cuadrado mágico permanece mágico cuando se transforma por cualquier elemento D4, el grupo de simetría de un cuadrado (ver grupo de orden Dihedral 8 § Grupo de simetría de un cuadrado: grupo dihedral del orden 8). Cada combinación de una o más rotaciones de 90 grados, reflexiones, o ambas producen ocho cuadrados trivialmente distintos que generalmente se consideran equivalentes. Se dice que los ocho cuadrados de este tipo conforman una única clase de equivalencia. Los ocho cuadrados mágicos equivalentes para la plaza mágica 3×3 se muestran a continuación:
- Un cuadrado mágico de orden n{displaystyle n}
 restos mágicos cuando sus filas y columnas son permutadas simétricamente por p{displaystyle p}
restos mágicos cuando sus filas y columnas son permutadas simétricamente por p{displaystyle p} tales que p()i)+p()n+1− − i)=n+1{displaystyle p(i)+p(n+1-i)=n+1}
tales que p()i)+p()n+1− − i)=n+1{displaystyle p(i)+p(n+1-i)=n+1} para 1≤ ≤ i≤ ≤ n{displaystyle 1leq ileq n}
para 1≤ ≤ i≤ ≤ n{displaystyle 1leq ileq n} . Cada permutación de las filas o columnas conserva todas las sumas de fila y columna, pero generalmente no las dos sumas diagonales. Si la misma permutación p{displaystyle p}
. Cada permutación de las filas o columnas conserva todas las sumas de fila y columna, pero generalmente no las dos sumas diagonales. Si la misma permutación p{displaystyle p} se aplica tanto a las filas como a las columnas, luego elemento diagonal en fila i{displaystyle i}
se aplica tanto a las filas como a las columnas, luego elemento diagonal en fila i{displaystyle i} y columna i{displaystyle i}
y columna i{displaystyle i} es mapeado a fila p()i){displaystyle p(i)}
es mapeado a fila p()i){displaystyle p(i)} y columna p()i){displaystyle p(i)}
y columna p()i){displaystyle p(i)} que está en la misma diagonal; por lo tanto, la aplicación de la misma permutación a filas y columnas conserva la suma diagonal principal (de izquierda a inferior derecha). Si la permutación es simétrica como se describe, entonces el elemento diagonal en fila i{displaystyle i}
que está en la misma diagonal; por lo tanto, la aplicación de la misma permutación a filas y columnas conserva la suma diagonal principal (de izquierda a inferior derecha). Si la permutación es simétrica como se describe, entonces el elemento diagonal en fila i{displaystyle i} y columna n+1− − i{displaystyle n+1-i}
y columna n+1− − i{displaystyle n+1-i} es mapeado a fila p()i){displaystyle p(i)}
es mapeado a fila p()i){displaystyle p(i)} y columna p()n+1− − i)=n+1− − p()i){displaystyle p(n+1-i)=n+1-p(i)}
y columna p()n+1− − i)=n+1− − p()i){displaystyle p(n+1-i)=n+1-p(i)} que está en la misma diagonal; por lo tanto, la aplicación de la misma permutación simétrica a ambas filas y columnas conserva ambas sumas diagonales. Para incluso n{displaystyle n}
que está en la misma diagonal; por lo tanto, la aplicación de la misma permutación simétrica a ambas filas y columnas conserva ambas sumas diagonales. Para incluso n{displaystyle n} , hay 2n2()n2)!{displaystyle 2^{frac}left({frac {n}right)}}}
, hay 2n2()n2)!{displaystyle 2^{frac}left({frac {n}right)}}} tales permutaciones simétricas, y 2n− − 12()n− − 12)!{displaystyle 2^{frac {n-1}{2}left({frac {n-1}right)}}} {fn1}}}
tales permutaciones simétricas, y 2n− − 12()n− − 12)!{displaystyle 2^{frac {n-1}{2}left({frac {n-1}right)}}} {fn1}}} para n{displaystyle n}
para n{displaystyle n} extraño. En el ejemplo a continuación, el cuadrado mágico original de la izquierda tiene sus filas y columnas simétricamente permutadas por ()4,6,5,2,1,3){displaystyle (4,6,5,2,1,3)}
extraño. En el ejemplo a continuación, el cuadrado mágico original de la izquierda tiene sus filas y columnas simétricamente permutadas por ()4,6,5,2,1,3){displaystyle (4,6,5,2,1,3)} dando lugar a la plaza mágica a la derecha.
dando lugar a la plaza mágica a la derecha.
| 1 | 32 | 33 | 4 | 35 | 6
| | 30 | 8 | 27 | 28 | 11 | 7
| | 13 | 23 | 22 | 21 | 14 | 18
| | 24 | 17 | 16 | 15 | 20 | 19
| | 12 | 26 | 10 | 9 | 29 | 25
| | 31 | 5 | 3 | 34 | 2 | 36
|
| | 29 | 9 | 25 | 12 | 10 | 26
| | 20 | 15 | 19 | 24 | 16 | 17
| | 2 | 34 | 36 | 31 | 3 | 5
| | 35 | 4 | 6 | 1 | 33 | 32
| | 14 | 21 | 18 | 13 | 22 | 23
| | 11 | 28 | 7 | 30 | 27 | 8
|
|
- Un cuadrado mágico de orden n{displaystyle n}
 permanece mágico cuando las filas i{displaystyle i}
permanece mágico cuando las filas i{displaystyle i} y ()n+1− − i){displaystyle (n+1-i)}
y ()n+1− − i){displaystyle (n+1-i)} se intercambian y se intercambian columnas i{displaystyle i}
se intercambian y se intercambian columnas i{displaystyle i} y ()n+1− − i){displaystyle (n+1-i)}
y ()n+1− − i){displaystyle (n+1-i)} se intercambian porque es una permutación simétrica de la forma descrita anteriormente. En el ejemplo a continuación, la plaza a la derecha se obtiene intercambiando las filas 1 y 4a y columnas de la plaza original a la izquierda.
se intercambian porque es una permutación simétrica de la forma descrita anteriormente. En el ejemplo a continuación, la plaza a la derecha se obtiene intercambiando las filas 1 y 4a y columnas de la plaza original a la izquierda.
| 1 | 15 | 14 | 4 | | 12 | 6 | 7 | 9
| | 8 | 10 | 11 | 5
| | 13 | 3 | 2 | 16 |
| | 16 | 3 | 2 | 13
| | 9 | 6 | 7 | 12
| | 5 | 10 | 11 | 8
| | 4 | 15 | 14 | 1
|
|
- Un cuadrado mágico de orden n{displaystyle n}
 permanece mágico cuando las filas i{displaystyle i}
permanece mágico cuando las filas i{displaystyle i} y j{displaystyle j}
y j{displaystyle j} son intercambiados, filas ()n+1− − i){displaystyle (n+1-i)}
son intercambiados, filas ()n+1− − i){displaystyle (n+1-i)} y ()n+1− − j){displaystyle (n+1-j)}
y ()n+1− − j){displaystyle (n+1-j)} se intercambian, columnas i{displaystyle i}
se intercambian, columnas i{displaystyle i} y j{displaystyle j}
y j{displaystyle j} se intercambian, y columnas ()n+1− − i){displaystyle (n+1-i)}
se intercambian, y columnas ()n+1− − i){displaystyle (n+1-i)} y ()n+1− − j){displaystyle (n+1-j)}
y ()n+1− − j){displaystyle (n+1-j)} se intercambian donde <math alttext="{displaystyle i<ji.j.n+12{displaystyle i hicieran {fn+1}{2}}<img alt="{displaystyle i<j porque esta es otra permutación simétrica de la forma descrita anteriormente. En el ejemplo a continuación, la plaza izquierda es la plaza original, mientras que la plaza derecha es la nueva plaza obtenida por esta transformación. En la plaza media se han intercambiado filas 1 y 2 y filas 3 y 4. La plaza final de la derecha se obtiene por las columnas intercambiadoras 1 y 2 y las columnas 3 y 4 de la plaza media. En este ejemplo particular, este transformado gira los cuadrantes 180 grados. La plaza media es también magia porque la plaza original es asociativa.
se intercambian donde <math alttext="{displaystyle i<ji.j.n+12{displaystyle i hicieran {fn+1}{2}}<img alt="{displaystyle i<j porque esta es otra permutación simétrica de la forma descrita anteriormente. En el ejemplo a continuación, la plaza izquierda es la plaza original, mientras que la plaza derecha es la nueva plaza obtenida por esta transformación. En la plaza media se han intercambiado filas 1 y 2 y filas 3 y 4. La plaza final de la derecha se obtiene por las columnas intercambiadoras 1 y 2 y las columnas 3 y 4 de la plaza media. En este ejemplo particular, este transformado gira los cuadrantes 180 grados. La plaza media es también magia porque la plaza original es asociativa.
| 1 | 15 | 14 | 4
| | 12 | 6 | 7 | 9
| | 8 | 10 | 11 | 5
| | 13 | 3 | 2 | 16
|
| | 12 | 6 | 7 | 9
| | 1 | 15 | 14 | 4
| | 13 | 3 | 2 | 16
| | 8 | 10 | 11 | 5
|
| | 6 | 12 | 9 | 7
| | 15 | 1 | 4 | 14
| | 3 | 13 | 16 | 2
| | 10 | 8 | 5 | 11
|
|
- Un cuadrado mágico permanece mágico cuando sus cuadrantes se intercambian diagonalmente porque esta es otra permutación simétrica de la forma descrita anteriormente. Por orden uniforme n{displaystyle n}
 , permute las filas y columnas por permutación p{displaystyle p}
, permute las filas y columnas por permutación p{displaystyle p} Donde p()i)=i+n2{displaystyle p(i)=i+{frac {n}{2}}
Donde p()i)=i+n2{displaystyle p(i)=i+{frac {n}{2}} para i≤ ≤ n2{displaystyle ileq {fnMicroc {n}{2}}
para i≤ ≤ n2{displaystyle ileq {fnMicroc {n}{2}} , y p()i)=i− − n2{displaystyle p(i)=i-{frac {n}{2}}
, y p()i)=i− − n2{displaystyle p(i)=i-{frac {n}{2}} para {frac {n}{2}}}" xmlns="http://www.w3.org/1998/Math/MathML">i■n2{displaystyle i {n}{2}}
para {frac {n}{2}}}" xmlns="http://www.w3.org/1998/Math/MathML">i■n2{displaystyle i {n}{2}}![]() {frac {n}{2}}}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/ae11d691aa39db15ed805380e604075f0ac54cfe" style="vertical-align: -1.838ex; width:6.132ex; height:4.676ex;"/>. Por orden extraño n{displaystyle n}
{frac {n}{2}}}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/ae11d691aa39db15ed805380e604075f0ac54cfe" style="vertical-align: -1.838ex; width:6.132ex; height:4.676ex;"/>. Por orden extraño n{displaystyle n} , filas y columnas de permutación p{displaystyle p}
, filas y columnas de permutación p{displaystyle p} Donde p()i)=i+n+12{displaystyle p(i)=i+{frac {n+1}{2}}
Donde p()i)=i+n+12{displaystyle p(i)=i+{frac {n+1}{2}} para <math alttext="{displaystyle ii.n+12{displaystyle i done{frac {n+1}{2}}<img alt="{displaystyle i, y p()i)=i− − n+12{displaystyle p(i)=i-{frac {n+1}{2}}
para <math alttext="{displaystyle ii.n+12{displaystyle i done{frac {n+1}{2}}<img alt="{displaystyle i, y p()i)=i− − n+12{displaystyle p(i)=i-{frac {n+1}{2}} para {frac {n+1}{2}}}" xmlns="http://www.w3.org/1998/Math/MathML">i■n+12{displaystyle i {n+1}{2}}
para {frac {n+1}{2}}}" xmlns="http://www.w3.org/1998/Math/MathML">i■n+12{displaystyle i {n+1}{2}}![]() {frac {n+1}{2}}}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/732bf3d15e45e49e79aa2302e10035440351b572" style="vertical-align: -1.838ex; width:10.135ex; height:5.176ex;"/>. Para la extraña plaza ordenada, las mitades de la fila central y la columna también se intercambian. Ejemplos para el orden 4 y 5 cuadrados mágicos se dan a continuación:
{frac {n+1}{2}}}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/732bf3d15e45e49e79aa2302e10035440351b572" style="vertical-align: -1.838ex; width:10.135ex; height:5.176ex;"/>. Para la extraña plaza ordenada, las mitades de la fila central y la columna también se intercambian. Ejemplos para el orden 4 y 5 cuadrados mágicos se dan a continuación:
| 1 | 15 | 14 | 4
| | 12 | 6 | 7 | 9
| | 8 | 10 | 11 | 5
| | 13 | 3 | 2 | 16
|
| | 11 | 5 | 8 | 10
| | 2 | 16 | 13 | 3
| | 14 | 4 | 1 | 15
| | 7 | 9 | 12 | 6
|
| | 17 | 24 | 1 | 8 | 15
| | 23 | 5 | 7 | 14 | 16
| | 4 | 6 | 13 | 20 | 22 | | 10 | 12 | 19 | 21 | 3
| | 11 | 18 | 25 | 2 | 9
|
| | 21 | 3 | 19 | 10 | 12
| | 2 | 9 | 25 | 11 | 18
| | 20 | 22 | 13 | 4 | 6
| | 8 | 15 | 1 | 17 | 24
| | 14 | 16 | 7 | 23 | 5
|
|
Para cuadrados mágicos asociativos
- Una plaza de magia asociativa permanece asociativa cuando se intercambian dos filas o columnas equidistas del centro. Para un cuadrado, hay n/2 pares de filas o columnas que pueden ser intercambiadas; por lo tanto 2n/2 × 2n/2 = 2n cuadrados mágicos equivalentes combinando tales intercambios se puede obtener. Para cuadrado extraño, hay (n - 1)/2 pares de filas o columnas que pueden ser intercambiadas; y 2n-1 cuadrados mágicos equivalentes obtenidos combinando tales intercambios. Intercambiar todas las filas gira la plaza verticalmente (es decir, reflejada a lo largo del eje horizontal), mientras que el intercambio de todas las columnas gira la casilla horizontalmente (es decir, reflejada a lo largo del eje vertical). En el ejemplo a continuación, un cuadrado mágico asociativo de 4×4 a la izquierda se transforma en un cuadrado a la derecha intercambiando la segunda y tercera fila, dando lugar a la famosa plaza mágica de Durer.
| 16 | 3 | 2 | 13
| | 9 | 6 | 7 | 12
| | 5 | 10 | 11 | 8
| | 4 | 15 | 14 | 1
|
| | 16 | 3 | 2 | 13
| | 5 | 10 | 11 | 8
| | 9 | 6 | 7 | 12
| | 4 | 15 | 14 | 1
|
|
- Una plaza de magia asociativa permanece asociativa cuando dos filas del mismo lado (o columnas) se intercambian junto con otras filas laterales correspondientes (o columnas). Para un cuadrado, ya que hay n/2 filas del mismo lado (o columnas), hay n()n - 2)/8 pares de tales filas (o columnas) que pueden ser intercambiadas. Así, 2n()n-2)/8 × 2n()n-2)/8 = 2n()n-2)/4 cuadrados mágicos equivalentes se pueden obtener combinando tales intercambios. Para extraño cuadrado, ya que hay (n - 1)/2 filas o columnas del mismo lado, hay (n - 1)n - 3)/8 pares de filas o columnas que pueden ser intercambiadas. Así, hay 2()n - 1)n 3)/8 × 2()n - 1)n 3)/8 = 2()n - 1)n - 3)/4 cuadrados mágicos equivalentes obtenidos combinando tales intercambios. Intercambiando todas las mismas filas laterales gira cada cuadrante de la plaza verticalmente, mientras que intercambiando todas las mismas columnas laterales gira cada cuadrante de la plaza horizontalmente. En el ejemplo a continuación, la plaza original está a la izquierda, cuyas filas 1 y 2 se intercambian entre sí, junto con las filas 3 y 4, para obtener la plaza transformada a la derecha.
| 1 | 15 | 14 | 4
| | 12 | 6 | 7 | 9
| | 8 | 10 | 11 | 5
| | 13 | 3 | 2 | 16
|
| | 12 | 6 | 7 | 9
| | 1 | 15 | 14 | 4
| | 13 | 3 | 2 | 16
| | 8 | 10 | 11 | 5
|
|
- Una plaza de magia asociativa permanece asociativa cuando sus entradas son reemplazadas por números correspondientes de un conjunto de s progresiones aritméticas con la misma diferencia común entre r términos, tal que r × s = n2, y cuyos términos iniciales también están en progresión aritmética, para obtener un cuadrado mágico no normal. Aquí. s o r debe ser un múltiples n. Vamos a tener s progresiones aritméticas dadas por
- aa+ca+2c⋯ ⋯ a+()r− − 1)ca+da+c+da+2c+d⋯ ⋯ a+()r− − 1)c+da+2da+c+2da+2c+2d⋯ ⋯ a+()r− − 1)c+2d⋯ ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ a+()s− − 1)da+c+()s− − 1)da+2c+()s− − 1)d⋯ ⋯ a+()r− − 1)c+()s− − 1)d{cccccc1cc1cdot]

- Donde a es el término inicial, c es la diferencia común de las progresiones aritméticas, y d es la diferencia común entre los términos iniciales de cada progresión. La nueva constante mágica será
- M=na+n2[()r− − 1)c+()s− − 1)d].{displaystyle M=na+{frac {n}{2}{big [}(r-1)c+(s-1)d{big ]}}
![{displaystyle M=na+{frac {n}{2}}{big [}(r-1)c+(s-1)d{big ]}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1315a1e80e660caa150524368fc718884b56906e)
- Si s = r = n, luego sigue la simplificación
- M=na+n2()n− − 1)()c+d).{displaystyle M=na+{frac {n} {2}(n-1)(c+d). }

- Con a = c = 1 y d = n, lo habitual M = n()n2+1)/2 se obtiene. For given M el requerido a, c, y d se puede encontrar resolviendo la ecuación lineal Diophantine. En los ejemplos a continuación, hay orden 4 cuadrados mágicos normales en la mayoría izquierda. El segundo cuadrado es un cuadrado mágico no normal correspondiente con r = 8, s = 2, a = 1, c = 1, y d = 10 tal que la nueva constante mágica es M = 38. El tercer cuadrado es un orden 5 cuadrado mágico normal, que es una versión rotativa de 90 grados de la plaza generada por el método De la Loubere. A la derecha la mayoría es un cuadrado mágico no normal correspondiente con a = 4, c = 1, y d = 6 tal que la nueva constante mágica es M = 90.
| 1 | 15 | 14 | 4
| | 12 | 6 | 7 | 9
| | 8 | 10 | 11 | 5
| | 13 | 3 | 2 | 16
|
| | 1 | 17 | 16 | 4
| | 14 | 6 | 7 | 11
| | 8 | 12 | 13 | 5
| | 15 | 3 | 2 | 18
|
| | 11 | 10 | 4 | 23 | 17
| | 18 | 12 | 6 | 5 | 24
| | 25 | 19 | 13 | 7 | 1
| | 2 | 21 | 20 | 14 | 8
| | 9 | 3 | 22 | 16 | 15
|
| | 16 | 14 | 7 | 30 | 23
| | 24 | 17 | 10 | 8 | 31
| | 32 | 25 | 18 | 11 | 4
| | 5 | 28 | 26 | 19 | 12
| | 13 | 6 | 29 | 22 | 20
|
|
Para cuadrados mágicos pandiagonales
- Un cuadrado mágico pan-diagonal sigue siendo un cuadrado mágico pan-diagonal bajo el cambio cíclico de filas o de columnas o ambos. Esto nos permite posicionar un número determinado en cualquiera de los n2 células de una n Orden cuadrado. Así, para un cuadrado pan-magic dado, hay n2 cuadrados pan-magicos equivalentes. En el ejemplo a continuación, la plaza original de la izquierda se transforma cambiando la primera fila a la parte inferior para obtener una nueva plaza pan-magic en el centro. A continuación, la 1a y 2a columna de la plaza pan-magic media se desplaza circularmente a la derecha para obtener una nueva plaza pan-magic a la derecha.
| 10 | 3 | 13 | 8
| | 5 | 16 | 2 | 11
| | 4 | 9 | 7 | 14
| | 15 | 6 | 12 | 1
|
| | 5 | 16 | 2 | 11
| | 4 | 9 | 7 | 14
| | 15 | 6 | 12 | 1
| | 10 | 3 | 13 | 8
|
| | 2 | 11 | 5 | 16
| | 7 | 14 | 4 | 9
| | 12 | 1 | 15 | 6
| | 13 | 8 | 10 | 3
|
|
Para cuadrados mágicos bordeados
- Una plaza de magia fronteriza sigue siendo una plaza de magia fronteriza después de permutar las células fronterizas en las filas o columnas, junto con sus correspondientes términos complementarios, manteniendo las celdas de esquina fijadas. Puesto que las células de cada fila y columna de cada frontera concéntrico pueden ser permutadas independientemente, cuando el orden n ≥ 5 es extraño, hay ((n-2)! × (n-4)! × ·· × 3!)2 equivalentes cuadrados fronterizos. Cuando n ≥ 6 (n-2)! × (n-4)! × ·· × 4!)2 equivalentes cuadrados fronterizos. En el ejemplo a continuación se da un cuadrado de orden 5 cuya fila fronteriza ha sido permutada y (3!)2 = 36 plazas equivalentes se pueden obtener.
| 1 | 23 | 16 | 4 | 21
| | 15 | 14 | 7 | 18 | 11
| | 24 | 17 | 13 | 9 | 2
| | 20 | 8 | 19 | 12 | 6
| | 5 | 3 | 10 | 22 | 25
|
| | 1 | 16 | 23 | 4 | 21
| | 15 | 14 | 7 | 18 | 11
| | 24 | 17 | 13 | 9 | 2
| | 20 | 8 | 19 | 12 | 6
| | 5 | 10 | 3 | 22 | 25
|
|
- Una plaza de magia fronteriza sigue siendo una plaza de magia fronteriza después de que cada una de sus fronteras concéntricas sean giradas o reflejadas independientemente con respecto a la plaza de magia central. Si hay b fronteras, entonces esta transformación producirá 8b cuadrados equivalentes. En el ejemplo debajo de la plaza mágica 5×5, la frontera ha sido rotada 90 grados a la vez.
| 1 | 23 | 16 | 4 | 21
| | 15 | 14 | 7 | 18 | 11
| | 24 | 17 | 13 | 9 | 2
| | 20 | 8 | 19 | 12 | 6
| | 5 | 3 | 10 | 22 | 25
|
| | 21 | 11 | 2 | 6 | 25
| | 4 | 14 | 7 | 18 | 22
| | 16 | 17 | 13 | 9 | 10
| | 23 | 8 | 19 | 12 | 3
| | 1 | 15 | 24 | 20 | 5
|
|
Para cuadrados mágicos compuestos
- Un cuadrado mágico compuesto sigue siendo un cuadrado mágico compuesto cuando los cuadrados mágicos embebidos experimentan transformaciones que no perturban la propiedad mágica (por ejemplo, rotación, reflexión, cambio de filas y columnas, etc.).
Métodos especiales de construcción
Durante el milenio, se han descubierto muchas formas de construir cuadrados mágicos. Estos métodos se pueden clasificar en métodos generales y métodos especiales, en el sentido de que los métodos generales nos permiten construir más de un único cuadrado mágico de un orden dado, mientras que los métodos especiales nos permiten construir un solo cuadrado mágico de un orden dado. Los métodos especiales son algoritmos específicos, mientras que los métodos generales pueden requerir algo de prueba y error.
Los métodos especiales son las formas estándar y más sencillas de construir un cuadrado mágico. Sigue ciertas configuraciones/fórmulas/algoritmos que generan patrones regulares de números en un cuadrado. La corrección de estos métodos especiales puede probarse utilizando uno de los métodos generales que se dan en secciones posteriores. Una vez que se ha construido un cuadrado mágico usando un método especial, las transformaciones descritas en la sección anterior se pueden aplicar para producir más cuadrados mágicos. Por lo general, se hace referencia a los métodos especiales utilizando el nombre del autor o autores (si se conocen) que describieron el método, p. El método de De la Loubere, el método de Starchey, el método de Bachet, etc.
Los cuadrados mágicos existen para todos los valores de n, excepto para el orden 2. Los cuadrados mágicos se pueden clasificar según su orden en impares, doblemente pares (n divisible por cuatro), e individualmente pares (n pares, pero no divisibles por cuatro). Esta clasificación se basa en el hecho de que es necesario emplear técnicas completamente diferentes para construir estas diferentes especies de cuadrados. Los cuadrados mágicos impares y doblemente pares son fáciles de generar; la construcción de cuadrados mágicos pares por separado es más difícil, pero existen varios métodos, incluido el método LUX para cuadrados mágicos (debido a John Horton Conway) y el método Strachey para cuadrados mágicos.
Un método para construir un cuadrado mágico de orden 3
En el siglo XIX, Édouard Lucas ideó la fórmula general para los cuadrados mágicos de orden 3. Considere la siguiente tabla compuesta por números enteros positivos a, b y c:
| c − b | c +a + b) | c − a |
| c −a − b) | c | c +a − b)
|
| c + a | c −a + b) | c + b |
Estos nueve números serán enteros positivos distintos que formarán un cuadrado mágico con la constante mágica 3c siempre que 0 < a < b < c − a y b ≠ 2a. Además, cada cuadrado mágico de 3×3 de enteros positivos distintos tiene esta forma.
En 1997, Lee Sallows descubrió que, dejando de lado las rotaciones y los reflejos, cada paralelogramo distinto dibujado en el diagrama de Argand define un cuadrado mágico único de 3×3, y viceversa, un resultado que nunca antes se había observado.
Un método para construir un cuadrado mágico de orden impar

Método de construcción de Yang Hui
Un método para construir cuadrados mágicos de orden impar fue publicado por el diplomático francés de la Loubère en su libro, Una nueva relación histórica del reino de Siam (Du Royaume de Siam, 1693), en el capítulo titulado El problema del cuadrado mágico según los indios. El método funciona de la siguiente manera:
El método prescribe comenzar en la columna central de la primera fila con el número 1. Después de eso, el movimiento fundamental para llenar los cuadrados es en diagonal hacia arriba y hacia la derecha, un paso a la vez. Si un cuadrado se llena con un múltiplo del orden n, uno se mueve verticalmente hacia abajo un cuadrado y luego continúa como antes. Cuando un "arriba y a la derecha" move dejaría el cuadrado, se envuelve alrededor de la última fila o la primera columna, respectivamente.
Es posible comenzar desde otros cuadrados en lugar de la columna central de la primera fila, pero solo las sumas de fila y columna serán idénticas y darán como resultado una suma mágica, mientras que las sumas diagonales serán diferentes. El resultado será así un cuadrado semimágico y no un verdadero cuadrado mágico. Moverse en direcciones distintas al noreste también puede generar cuadrados mágicos.
| Orden 5
| 17 | 24 | 1 | 8 | 15
| | 23 | 5 | 7 | 14 | 16
| | 4 | 6 | 13 | 20 | 22
| | 10 | 12 | 19 | 21 | 3
| | 11 | 18 | 25 | 2 | 9
| | Ordenanza 9
| 47 | 58 | 69 | 80 | 1 | 12 | 23 | 34 | 45
| | 57 | 68 | 79 | 9 | 11 | 22 | 33 | 44 | 46
| | 67 | 78 | 8 | 10 | 21 | 32 | 43 | 54 | 56
| | 77 | 7 | 18 | 20 | 31 | 42 | 53 | 55 | 66
| | 6 | 17 | 19 | 30 | 41 | 52 | 63 | 65 | 76
| | 16 | 27 | 29 | 40 | 51 | 62 | 64 | 75 | 5
| | 26 | 28 | 39 | 50 | 61 | 72 | 74 | 4 | 15
| | 36 | 38 | 49 | 60 | 71 | 73 | 3 | 14 | 25
| | 37 | 48 | 59 | 70 | 81 | 2 | 13 | 24 | 35
| |
Un método para construir un cuadrado mágico de orden doblemente uniforme
Doblemente par significa que n es un múltiplo par de un entero par; o 4p (por ejemplo, 4, 8, 12), donde p es un número entero.
Patrón genérico
Todos los números están escritos en orden de izquierda a derecha en cada fila, comenzando desde la esquina superior izquierda. Luego, los números se retienen en el mismo lugar o se intercambian con sus números diametralmente opuestos en un cierto patrón regular. En el cuadrado mágico de orden cuatro, los números de los cuatro cuadrados centrales y un cuadrado en cada esquina se mantienen en el mismo lugar y los demás se intercambian con sus números diametralmente opuestos.
Una construcción de un cuadrado mágico de orden 4
Comenzando desde arriba a la izquierda, ve de izquierda a derecha a través de cada fila del cuadrado, contando cada celda del 1 al 16 y llenando las celdas a lo largo de las diagonales con su número correspondiente. Una vez que llegue a la celda inferior derecha, continúe yendo de derecha a izquierda, comenzando desde la parte inferior derecha de la tabla a través de cada fila, y complete las celdas no diagonales contando del 1 al 16 con su número correspondiente. Como se muestra abajo:
M = Orden 4
| 1 | | | 4
| | 6 | 7 | | | 10 | 11 | | | 13 | | | 16
| | M = Orden 4
| 1 | 15 | 14 | 4
| | 12 | 6 | 7 | 9
| | 8 | 10 | 11 | 5
| | 13 | 3 | 2 | 16
| |
Una extensión del ejemplo anterior para los pedidos 8 y 12
Primero genere una tabla de patrones, donde un '1' indica seleccionar del cuadrado donde los números están escritos en orden del 1 al n2 (de izquierda a derecha, de arriba a abajo), y un '0' indica seleccionar del cuadrado donde los números están escritos en orden inverso n2 a 1. Para M = 4, la tabla de patrones es como se muestra abajo (tercera matriz desde la izquierda). Con las celdas inalteradas (celdas con '1') sombreadas, se obtiene un patrón entrecruzado.
M = Orden 4
| 1 | 2 | 3 | 4
| | 5 | 6 | 7 | 8
| | 9 | 10 | 11 | 12
| | 13 | 14 | 15 | 16
| | M = Orden 4
| 16 | 15 | 14 | 13
| | 12 | 11 | 10 | 9
| | 8 | 7 | 6 | 5
| | 4 | 3 | 2 | 1
| | M = Orden 4
| 1 | 0 | 0 | 1
| | 0 | 1 | 1 | 0
| | 0 | 1 | 1 | 0
| | 1 | 0 | 0 | 1
| | M = Orden 4
| 1 | 15 | 14 | 4
| | 12 | 6 | 7 | 9
| | 8 | 10 | 11 | 5
| | 13 | 3 | 2 | 16
| |
Los patrones son a) hay el mismo número de '1' y '0' en cada fila y columna; b) cada fila y cada columna son "palindrómicos"; c) las mitades izquierda y derecha son imágenes especulares; y d) las mitades superior e inferior son imágenes especulares (c y d implican b). La tabla de patrones se puede denotar usando hexadecimales como (9, 6, 6, 9) por simplicidad (1-nibble por fila, 4 filas). El método más simple para generar el patrón requerido para cuadrados doblemente pares de mayor orden es copiar el patrón genérico para el cuadrado de cuarto orden en cada subcuadrado de cuatro por cuatro.
Para M = 8, las opciones posibles para el patrón son (99, 66, 66, 99, 99, 66, 66, 99); (3C, 3C, C3, C3, C3, C3, 3C, 3C); (A5, 5A, A5, 5A, 5A, A5, 5A, A5) (2 mordiscos por fila, 8 filas).
M = Orden 8
| 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1
| | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0
| | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0
| | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1
| | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1
| | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0
| | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0
| | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1
| | M = Orden 8
| 1 | | | 4 | 5 | | | 8
| | 10 | 11 | | | 14 | 15 | | | 18 | 19 | | | 22 | 23 | | | 25 | | | 28 | 29 | | | 32
| | 33 | | | 36 | 37 | | | 40
| | 42 | 43 | | | 46 | 47 | | | 50 | 51 | | | 54 | 55 | | | 57 | | | 60 | 61 | | | 64
| | M = Orden 8
| 1 | 63 | 62 | 4 | 5 | 59 | 58 | 8
| | 56 | 10 | 11 | 53 | 52 | 14 | 15 | 49
| | 48 | 18 | 19 | 45 | 44 | 22 | 23 | 41
| | 25 | 39 | 38 | 28 | 29 | 35 | 34 | 32
| | 33 | 31 | 30 | 36 | 37 | 27 | 26 | 40
| | 24 | 42 | 43 | 21 | 20 | 46 | 47 | 17
| | 16 | 50 | 51 | 13 | 12 | 54 | 55 | 9
| | 57 | 7 | 6 | 60 | 61 | 3 | 2 | 64
| |
Para M = 12, la tabla de patrones (E07, E07, E07, 1F8, 1F8, 1F8, 1F8, 1F8, 1F8, E07, E07, E07) produce un cuadrado mágico (3 nibbles por fila, 12 filas).) Es posible contar el número de opciones que uno tiene basándose en la tabla de patrones, teniendo en cuenta las simetrías rotacionales.
Método de superposición
El primer descubrimiento del método de superposición lo hizo el matemático indio Narayana en el siglo XIV. El mismo método fue redescubierto y estudiado más tarde a principios del siglo XVIII en Europa por de la Loubere, Poignard, de La Hire y Sauveur; y el método generalmente se denomina método de de la Hire. Aunque el trabajo de Euler sobre el cuadrado mágico no era original, él conjeturó la imposibilidad de construir los cuadrados greco-latinos mutuamente ortogonales ordenados impares. Esta conjetura fue refutada a mediados del siglo XX. Para mayor claridad de exposición, se pueden distinguir dos variaciones importantes de este método.
Método de Euler
Este método consiste en construir dos cuadrados preliminares, que al sumarlos dan el cuadrado mágico. Como ejemplo, se considera un cuadrado mágico de 3×3. Cada número del cuadrado natural de 3 × 3 por un par de números se puede etiquetar como
donde cada par de alfabetos griego y latino, p. αa, están destinados a sumarse, es decir, αa = α + a. Aquí, (α, β, γ) = (0, 3, 6) y (a, b, c) = (1, 2, 3). Los números 0, 3 y 6 se denominan números raíz, mientras que los números 1, 2 y 3 se denominan números primarios. Una restricción general importante aquí es
- a La carta griega está emparejada con una carta latina sólo una vez.
Por lo tanto, el cuadrado original ahora se puede dividir en dos cuadrados más simples:
Los cuadrados con letras se denominan cuadrado griego o cuadrado latino si están rellenos con letras griegas o latinas, respectivamente. Se puede construir un cuadrado mágico asegurándose de que los cuadrados griegos y latinos también sean cuadrados mágicos. Lo contrario de esta declaración también es a menudo, pero no siempre (por ejemplo, cuadrados mágicos bordeados), cierto: un cuadrado mágico se puede descomponer en un cuadrado griego y uno latino, que son en sí mismos cuadrados mágicos. Por lo tanto, el método es útil tanto para la síntesis como para el análisis de un cuadrado mágico. Por último, al examinar el patrón en el que se disponen los números en el cuadrado terminado, a menudo es posible idear un algoritmo más rápido para construir cuadrados de orden superior que repliquen el patrón dado, sin la necesidad de crear el griego y el latín preliminares. cuadrícula.
Durante la construcción del cuadrado mágico de 3×3, los cuadrados griegos y latinos con solo tres términos únicos son mucho más fáciles de manejar que el cuadrado original con nueve términos diferentes. La suma de las filas y la suma de las columnas del cuadrado griego será la misma, α + β + γ, si
- cada letra aparece exactamente una vez en una columna dada o una fila.
Esto se puede lograr mediante la permutación cíclica de α, β y γ. El cumplimiento de estas dos condiciones asegura que el cuadrado resultante sea un cuadrado semimágico; y se dice que tales cuadrados griegos y latinos son mutuamente ortogonales entre sí. Para un orden n dado, hay como máximo n - 1 cuadrados en un conjunto de cuadrados mutuamente ortogonales, sin contar las variaciones debidas a la permutación de los símbolos. Este límite superior es exacto cuando n es un número primo.
Para construir un cuadrado mágico, también debemos asegurarnos de que las diagonales sumen una constante mágica. Para ello, tenemos una tercera condición:
- o todas las letras deben aparecer exactamente una vez en ambas diagonales; o en caso de casillas ordenadas impares, una de las diagonales debe consistir enteramente del término medio, mientras que la otra diagonal debe tener todas las letras exactamente una vez.
Los cuadrados griegos y latinos mutuamente ortogonales que satisfacen la primera parte de la tercera condición (que todas las letras aparezcan en ambas diagonales) se dice que son cuadrados greco-latinos doblemente diagonales mutuamente ortogonales.
Cuadrados impares: Para el cuadrado impar de 3×3, dado que α, β y γ son en progresión aritmética, su suma es igual al producto del orden del cuadrado y el término medio, es decir, α + β + γ = 3 β. Así, las sumas de las diagonales serán iguales si tenemos βs en la diagonal principal y α, β, γ en la diagonal sesgada. Del mismo modo, para el cuadrado latino. Los cuadrados griegos y latinos resultantes y su combinación serán los siguientes. El cuadrado latino es solo una rotación de 90 grados en sentido contrario a las agujas del reloj del cuadrado griego (o de manera equivalente, girando sobre el eje vertical) con las letras correspondientes intercambiadas. Sustituyendo los valores de las letras griegas y latinas se obtendrá el cuadrado mágico de 3×3.
Para los cuadrados impares, este método explica por qué funciona el método siamés (método de De la Loubere) y sus variantes. Este método básico se puede utilizar para construir cuadrados mágicos de órdenes impares de órdenes superiores. Resumir:
- Para extraños cuadrados ordenados, para construir la plaza griega, colocar el término medio a lo largo de la diagonal principal, y colocar el resto de los términos a lo largo de la diagonal skew. Las células vacías restantes están llenas por movimientos diagonales. La plaza latina se puede construir girando o girando la plaza griega, y reemplazando los alfabetos correspondientes. La plaza mágica se obtiene añadiendo los cuadrados griegos y latinos.
Una peculiaridad del método de construcción anterior para los cuadrados mágicos impares es que el número del medio (n2 + 1)/2 siempre aparecerá en la celda central del cuadrado mágico. Ya que hay (n - 1)! maneras de organizar los términos diagonales sesgados, podemos obtener (n - 1)! cuadrados griegos de esta manera; Lo mismo con los cuadrados latinos. Además, dado que cada cuadrado griego se puede emparejar con (n - 1)! cuadrados latinos, y dado que para cada cuadrado griego el término medio puede colocarse arbitrariamente en la diagonal principal o en la diagonal oblicua (y correspondientemente a lo largo de la diagonal oblicua o la diagonal principal para los cuadrados latinos), podemos construir un total de 2 × (n - 1)! × (n - 1)! cuadrados mágicos utilizando este método. Para n = 3, 5 y 7, esto dará 8, 1152 y 1,036,800 cuadrados mágicos diferentes, respectivamente. Dividiendo por 8 para despreciar los cuadrados equivalentes debido a la rotación y los reflejos, obtenemos 1, 144 y 129 600 cuadrados mágicos esencialmente diferentes, respectivamente.
Como otro ejemplo, se da la construcción de un cuadrado mágico de 5×5. Los números se escriben directamente en lugar de los alfabetos. Los cuadrados numerados se denominan cuadrado principal o cuadrado raíz si se rellenan con números primarios o números raíz, respectivamente. Los números se colocan sobre la diagonal sesgada en el cuadrado raíz de manera que la columna central del cuadrado raíz resultante tenga 0, 5, 10, 15, 20 (de abajo hacia arriba). El cuadrado principal se obtiene girando el cuadrado raíz en sentido antihorario 90 grados y reemplazando los números. El cuadrado resultante es un cuadrado mágico asociativo, en el que cada par de números simétricamente opuestos al centro suman el mismo valor, 26. Por ejemplo, 16+10, 3+23, 6+20, etc. En el cuadrado terminado, 1 se coloca en la celda central de la fila inferior y los números sucesivos se colocan mediante el movimiento del caballo alargado (dos celdas a la derecha, dos celdas hacia abajo) o, de manera equivalente, el movimiento del alfil (dos celdas en diagonal hacia abajo a la derecha). Cuando ocurre una colisión, el movimiento de ruptura es mover una celda hacia arriba. Todos los números impares se encuentran dentro del rombo central formado por 1, 5, 25 y 21, mientras que los números pares se ubican en las esquinas. La ocurrencia de los números pares se puede deducir copiando el cuadrado a los lados adyacentes. Los números pares de cuatro cuadrados adyacentes formarán una cruz.
| | | 10 | 15 | 20 | 0 | 5
| | 5 | 10 | 15 | 20 | 0
| | 0 | 5 | 10 | 15 | 20
| | 20 | 0 | 5 | 10 | 15
| | 15 | 20 | 0 | 5 | 10
|
| | 2 | 1 | 5 | 4 | 3
| | 1 | 5 | 4 | 3 | 2
| | 5 | 4 | 3 | 2 | 1
| | 4 | 3 | 2 | 1 | 5
| | 3 | 2 | 1 | 5 | 4
|
| | 12 | 16 | 25 | 4 | 8
| | 6 | 15 | 19 | 23 | 2
| | 5 | 9 | 13 | 17 | 21
| | 24 | 3 | 7 | 11 | 20 | 24
| | 18 | 22 | 1 | 10 | 14 | 18 | 22
| | | | 4 | 8 | 12 | 16
| | | | | 2 | 6
|
|
A continuación se muestra una variación del ejemplo anterior, donde la secuencia diagonal sesgada se toma en un orden diferente. El cuadrado mágico resultante es la versión invertida del famoso cuadrado mágico de Marte de Agrippa. Es un cuadrado mágico asociativo y es el mismo que produce el método de Moschopoulos. Aquí, el cuadrado resultante comienza con 1 colocado en la celda que está a la derecha de la celda central, y procede como el método de De la Loubere, con movimiento hacia abajo a la derecha. Cuando ocurre una colisión, el movimiento de ruptura es desplazar dos celdas a la derecha.
| | 10 | 0 | 15 | 5 | 20
| | 20 | 10 | 0 | 15 | 5
| | 5 | 20 | 10 | 0 | 15
| | 15 | 5 | 20 | 10 | 0
| | 0 | 15 | 5 | 20 | 10
|
| | 1 | 4 | 2 | 5 | 3
| | 4 | 2 | 5 | 3 | 1
| | 2 | 5 | 3 | 1 | 4
| | 5 | 3 | 1 | 4 | 2
| | 3 | 1 | 4 | 2 | 5
|
| | 11 | 4 | 17 | 10 | 23
| | 24 | 12 | 5 | 18 | 6
| | 7 | 25 | 13 | 1 | 19
| | 20 | 8 | 21 | 14 | 2
| | 3 | 16 | 9 | 22 | 15
|
|
En los ejemplos anteriores, para el cuadrado griego, la segunda fila se puede obtener de la primera fila desplazándola circularmente hacia la derecha una celda. De manera similar, la tercera fila es una versión desplazada circularmente de la segunda fila una celda a la derecha; etcétera. Asimismo, las filas del cuadrado latino se desplazan circularmente hacia la izquierda una celda. Los cambios de fila para los cuadrados griegos y latinos están en direcciones opuestas entre sí. Es posible desplazar circularmente las filas en más de una celda para crear el cuadrado griego y latino.
- Para plazas ordenadas, cuyo orden no es divisible por tres, podemos crear las plazas griegas cambiando una fila por dos lugares a la izquierda o a la derecha para formar la siguiente fila. La plaza latina se hace girando la plaza griega a lo largo de la diagonal principal e intercambiando las letras correspondientes. Esto nos da una plaza latina cuyas filas se crean cambiando la fila en la dirección contraria a la de la plaza griega. Una plaza griega y una plaza latina deben ser emparejados de tal manera que sus turnos de fila están en dirección mutuamente opuesta. La plaza mágica se obtiene añadiendo los cuadrados griegos y latinos. Cuando el pedido también resulta ser un número primo, este método siempre crea cuadrado mágico pandiagonal.
Esto esencialmente recrea el movimiento del caballo. Todas las letras aparecerán en ambas diagonales, asegurando la suma diagonal correcta. Ya que hay n! permutaciones de las letras griegas mediante las cuales podemos crear la primera fila del cuadrado griego, hay n! Cuadrados griegos que se pueden crear desplazando la primera fila en una dirección. Del mismo modo, hay n! tales cuadrados latinos creados al cambiar la primera fila en la dirección opuesta. Dado que un cuadrado griego se puede combinar con cualquier cuadrado latino con cambios de fila opuestos, ¡hay n! × n! tales combinaciones. Por último, dado que el cuadrado griego se puede crear desplazando las filas hacia la izquierda o hacia la derecha, ¡hay un total de 2 × n! × n! cuadrados mágicos que se pueden formar con este método. Para n = 5 y 7, ya que son números primos, este método crea 28.800 y 50.803.200 cuadrados mágicos pandiagonales. Dividiendo por 8 para despreciar los cuadrados equivalentes debido a la rotación y las reflexiones, obtenemos 3.600 y 6.350.400 cuadrados equivalentes. Dividiendo aún más por n2 para despreciar los cuadrados panmágicos equivalentes debido al cambio cíclico de filas o columnas, obtenemos 144 y 129 600 cuadrados panmágicos esencialmente diferentes. Para pedidos de 5 cuadrados, estos son los únicos cuadrados panmágicos que hay. La condición de que el orden del cuadrado no sea divisible por 3 significa que no podemos construir cuadrados de orden 9, 15, 21, 27, etc., por este método.
En el siguiente ejemplo, el cuadrado se ha construido de manera que el 1 está en la celda central. En el cuadro terminado, los números se pueden enumerar continuamente por el movimiento del caballo (dos celdas hacia arriba, una celda hacia la derecha). Cuando ocurre una colisión, el movimiento de ruptura es mover una celda hacia arriba, una celda hacia la izquierda. El cuadrado resultante es un cuadrado mágico pandiagonal. Este cuadrado también tiene una propiedad diabólica adicional de que cinco celdas cualesquiera en un patrón de tresbolillo formado por cualquier subcuadrado impar, incluido el envolvente, suman la constante mágica, 65. Por ejemplo, 13+7+1+20+24, 23+ 1+9+15+17, 13+21+10+19+2 etc. También las cuatro esquinas de cualquier cuadrado de 5×5 y la celda central, así como las celdas del medio de cada lado junto con la celda central, incluyendo envuelve, da la suma mágica: 13+10+19+22+1 y 20+24+12+8+1. Por último, los cuatro romboides que forman cruces alargadas también dan la suma mágica: 23+1+9+24+8, 15+1+17+20+12, 14+1+18+13+19, 7+1+25+ 22+10.
| 10 | 15 | 20 | 0 | 5
| | 0 | 5 | 10 | 15 | 20
| | 15 | 20 | 0 | 5 | 10
| | 5 | 10 | 15 | 20 | 0
| | 20 | 0 | 5 | 10 | 15
|
| | 3 | 1 | 4 | 2 | 5
| | 4 | 2 | 5 | 3 | 1
| | 5 | 3 | 1 | 4 | 2
| | 1 | 4 | 2 | 5 | 3
| | 2 | 5 | 3 | 1 | 4
|
| | 13 | 16 | 24 | 2 | 10
| | 4 | 7 | 15 | 18 | 21
| | 20 | 23 | 1 | 9 | 12
| | 6 | 14 | 17 | 25 | 3
| | 22 | 5 | 8 | 11 | 19
|
|
También podemos combinar los cuadrados griegos y latinos construidos por diferentes métodos. En el siguiente ejemplo, la casilla principal se crea con el movimiento del caballo. Hemos recreado el cuadrado mágico obtenido por el método de De la Loubere. ¡Como antes, podemos formar 8 × (n - 1)! × n! cuadrados mágicos por esta combinación. Para n = 5 y 7, esto creará 23 040 y 29 030 400 cuadrados mágicos. Después de dividir por 8 para despreciar los cuadrados equivalentes debido a la rotación y la reflexión, obtenemos 2.880 y 3.628.800 cuadrados.
| 15 | 20 | 0 | 5 | 10
| | 20 | 0 | 5 | 10 | 15
| | 0 | 5 | 10 | 15 | 20
| | 5 | 10 | 15 | 20 | 0
| | 10 | 15 | 20 | 0 | 5
|
| | 2 | 4 | 1 | 3 | 5
| | 3 | 5 | 2 | 4 | 1
| | 4 | 1 | 3 | 5 | 2
| | 5 | 2 | 4 | 1 | 3
| | 1 | 3 | 5 | 2 | 4
|
| | 17 | 24 | 1 | 8 | 15
| | 23 | 5 | 7 | 14 | 16
| | 4 | 6 | 13 | 20 | 22
| | 10 | 12 | 19 | 21 | 3
| | 11 | 18 | 25 | 2 | 9
|
|
Para cuadrados de orden 5, estos tres métodos dan un censo completo de la cantidad de cuadrados mágicos que se pueden construir mediante el método de superposición. Despreciando la rotación y las reflexiones, el número total de cuadrados mágicos de orden 5 producidos por el método de superposición es 144 + 3600 + 2880 = 6624.
Cuadrados pares: También podemos construir cuadrados ordenados pares de esta manera. Dado que no existe un término medio entre los alfabetos griego y latino para los cuadrados incluso ordenados, además de la restricción de los dos primeros, para que las sumas diagonales produzcan la constante mágica, todas las letras del alfabeto deben aparecer en la diagonal principal y en la diagonal. diagonal sesgada.
A continuación se muestra un ejemplo de un cuadrado de 4×4. Para la diagonal dada y la diagonal sesgada en el cuadrado griego, el resto de las celdas se pueden llenar con la condición de que cada letra aparezca solo una vez en una fila y una columna.
| | | | αa | βb | γc | δd
| | γd | δc | αb | βa
| | δb | γa | βd | αc
| | βc | αd | δa | γb
|
| | 1 | 6 | 11 | 16
| | 12 | 15 | 2 | 5
| | 14 | 9 | 8 | 3
| | 7 | 4 | 13 | 10
|
|
Usando estos dos cuadrados greco-latinos, ¡podemos construir 2 × 4! × 4! = 1,152 cuadrados mágicos. Dividiendo por 8 para eliminar los cuadrados equivalentes debido a la rotación y los reflejos, obtenemos 144 cuadrados mágicos esencialmente diferentes de orden 4. Estos son los únicos cuadrados mágicos construibles por el método de Euler, ya que solo hay dos cuadrados greco-latinos doblemente diagonales mutuamente ortogonales de orden 4.
Del mismo modo, se puede construir un cuadrado mágico de 8×8 como se muestra a continuación. Aquí el orden de aparición de los números no es importante; sin embargo, los cuadrantes imitan el patrón de diseño de los cuadrados greco-latinos de 4 × 4.
| 0 | 8 | 16 | 24 | 32 | 40 | 48 | 56
| | 24 | 16 | 8 | 0 | 56 | 48 | 40 | 32
| | 48 | 56 | 32 | 40 | 16 | 24 | 0 | 8
| | 40 | 32 | 56 | 48 | 8 | 0 | 24 | 16
| | 56 | 48 | 40 | 32 | 24 | 16 | 8 | 0
| | 32 | 40 | 48 | 56 | 0 | 8 | 16 | 24
| | 8 | 0 | 24 | 16 | 40 | 32 | 56 | 48
| | 16 | 24 | 0 | 8 | 48 | 56 | 32 | 40
|
| | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8
| | 3 | 4 | 1 | 2 | 7 | 8 | 5 | 6
| | 5 | 6 | 7 | 8 | 1 | 2 | 3 | 4
| | 7 | 8 | 5 | 6 | 3 | 4 | 1 | 2
| | 4 | 3 | 2 | 1 | 8 | 7 | 6 | 5
| | 2 | 1 | 4 | 3 | 6 | 5 | 8 | 7
| | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1
| | 6 | 5 | 8 | 7 | 2 | 1 | 4 | 3
|
| | 1 | 10 | 19 | 28 | 37 | 46 | 55 | 64
| | 27 | 20 | 9 | 2 | 63 | 56 | 45 | 38
| | 53 | 62 | 39 | 48 | 17 | 26 | 3 | 12
| | 47 | 40 | 61 | 54 | 11 | 4 | 25 | 18
| | 60 | 51 | 42 | 33 | 32 | 23 | 14 | 5
| | 34 | 41 | 52 | 59 | 6 | 13 | 24 | 31
| | 16 | 7 | 30 | 21 | 44 | 35 | 58 | 49
| | 22 | 29 | 8 | 15 | 50 | 57 | 36 | 43
|
|
El método de Euler ha dado lugar al estudio de los cuadrados greco-latinos. El método de Euler para construir cuadrados mágicos es válido para cualquier orden excepto el 2 y el 6.
Variaciones: Los cuadrados mágicos construidos a partir de cuadrados greco-latinos de doble diagonal mutuamente ortogonales son interesantes en sí mismos ya que la propiedad mágica surge de la posición relativa de los alfabetos en el cuadrado, y no debido a ninguna aritmética. propiedad del valor que se les haya asignado. Esto significa que podemos asignar cualquier valor a los alfabetos de dichos cuadrados y aun así obtener un cuadrado mágico. Esta es la base para construir cuadrados que muestren alguna información (por ejemplo, cumpleaños, años, etc.) en el cuadrado y para crear "cuadrados reversibles". Por ejemplo, podemos mostrar el número π ≈ 3.141592 en la fila inferior de un cuadrado mágico de 4×4 usando el cuadrado greco-latino dado arriba asignando (α, β, γ, δ) = (10, 0, 90, 15) y (a, b, c, d) = (0, 2, 3, 4). Obtendremos el siguiente cuadrado mágico no normal con la suma mágica 124:
| 10 | 2 | 93 | 19
|
| 94 | 18 | 12 | 0
|
| 17 | 90 | 4 | 13
|
| 3 | 14 | 15 | 92
|
Método de Narayana-De la Hire para órdenes pares
El método de Narayana-De la Hire para los cuadrados impares es el mismo que el de Euler. Sin embargo, para cuadrados pares, eliminamos el segundo requisito de que cada letra griega y latina aparezca solo una vez en una fila o columna determinada. Esto nos permite aprovechar que la suma de una progresión aritmética con un número par de términos es igual a la suma de dos términos simétricos opuestos multiplicada por la mitad del número total de términos. Así, al construir los cuadrados griegos o latinos,
- para cuadrados incluso ordenados, una carta puede aparecer n/2 veces en una columna pero sólo una vez seguida, o viceversa.
Como ejemplo, si tomamos un cuadrado de 4×4, donde los términos griegos y latinos tienen los valores (α, β, γ, δ) = (0, 4, 8, 12) y (a, b, c, d) = (1, 2, 3, 4), respectivamente, entonces tenemos α + β + γ + δ = 2 (α + δ) = 2 (β + γ). Del mismo modo, a + b + c + d = 2 (a + d) = 2 (b + c). Esto significa que el par complementario α y δ (o β y γ) puede aparecer dos veces en una columna (o una fila) y aún dar la suma mágica deseada. Así, podemos construir:
- Para incluso cuadrados ordenados, la plaza de magia griega se hace colocando primero los alfabetos griegos a lo largo de la diagonal principal en algún orden. La diagonal del puño se llena en el mismo orden o eligiendo los términos que son complementarios a los términos en la diagonal principal. Finalmente, las células restantes se llenan de la columna sabia. Dada una columna, utilizamos los términos complementarios en las células diagonales intersectadas por esa columna, asegurándonos de que aparecen sólo una vez en una fila determinada, pero n/2 veces en la columna dada. La plaza latina se obtiene girando o girando la plaza griega e intercambiando los alfabetos correspondientes. El cuadrado mágico final se obtiene añadiendo los cuadrados griegos y latinos.
En el ejemplo que se muestra a continuación, la diagonal principal (de arriba a la izquierda a abajo a la derecha) se llena con una secuencia ordenada como α, β, γ, δ, mientras que la diagonal sesgada (de abajo a la izquierda a arriba a la derecha) se llenó en el mismo orden. Luego, las celdas restantes se llenan en forma de columna de modo que las letras complementarias aparezcan solo una vez dentro de una fila, pero dos veces dentro de una columna. En la primera columna, dado que α aparece en la 1.ª y 4.ª fila, las celdas restantes se rellenan con su término complementario δ. Del mismo modo, las celdas vacías de la segunda columna se rellenan con γ; en la 3.ª columna β; y 4ª columna α. Cada letra griega aparece solo una vez en las filas, pero dos veces en las columnas. Como tal, las sumas de las filas son α + β + γ + δ mientras que las sumas de las columnas son 2 (α + δ) o 2 (β + γ). Lo mismo ocurre con el cuadrado latino, que se obtiene volcando el cuadrado griego a lo largo de la diagonal principal e intercambiando las letras correspondientes.
| | | | αa | γd | βd | δa
| | δc | βb | γb | αc
| | δb | βc | γc | αb
| | αd | γa | βa | δd
|
| | 1 | 12 | 8 | 13
| | 15 | 6 | 10 | 3
| | 14 | 7 | 11 | 2
| | 4 | 9 | 5 | 16
|
|
El ejemplo anterior explica por qué el "entrecruzado" método para trabajos doblemente iguales de cuadrados mágicos. Otro posible cuadrado mágico de 4 × 4, que también es pan-diagonal y también el más perfecto, se construye a continuación usando la misma regla. Sin embargo, la secuencia diagonal se elige de manera que las cuatro letras α, β, γ, δ aparezcan dentro de la subcuadrado central de 2×2. Las celdas restantes se llenan en forma de columna, de modo que cada letra aparece solo una vez dentro de una fila. En la primera columna, las celdas vacías deben llenarse con una de las letras seleccionadas del par complementario α y δ. Dada la primera columna, la entrada en la segunda fila solo puede ser δ ya que α ya está en la segunda fila; mientras que, en la 3ra fila la entrada solo puede ser α ya que δ ya está presente en la 3ra fila. Procedemos de manera similar hasta llenar todas las celdas. El cuadrado latino que se muestra a continuación se obtuvo girando el cuadrado griego a lo largo de la diagonal principal y reemplazando los alfabetos griegos con los alfabetos latinos correspondientes.
| | | | αa | βd | δa | γd
| | δb | γc | αb | βc
| | αd | βa | δd | γa
| | δc | γb | αc | βb
|
| | 1 | 8 | 13 | 12
| | 14 | 11 | 2 | 7
| | 4 | 5 | 16 | 9
| | 15 | 10 | 3 | 6
|
|
Podemos usar este enfoque para construir también cuadrados mágicos individuales. Sin embargo, tenemos que ser más cuidadosos en este caso ya que el criterio de emparejar los alfabetos griego y latino de forma única no se cumple automáticamente. La violación de esta condición lleva a que falten algunos números en el cuadro final, mientras que otros se duplican. Por lo tanto, aquí hay una condición importante:
- Para los cuadrados cantados, incluso en la plaza griega, compruebe las células de las columnas que se unen verticalmente a su complemento. En tal caso, la célula correspondiente de la plaza latina debe contener la misma letra que su célula horizontalmente emparejada.
A continuación se muestra una construcción de un cuadrado mágico de 6×6, donde los números se dan directamente, en lugar de los alfabetos. El segundo cuadrado se construye volteando el primer cuadrado a lo largo de la diagonal principal. Aquí, en la primera columna del cuadrado de la raíz, la tercera celda está emparejada con su complemento en las cuartas celdas. Por lo tanto, en el cuadrado principal, los números en la primera y sexta celda de la tercera fila son iguales. Asimismo, con otras columnas y filas. En este ejemplo, la versión invertida de la raíz cuadrada cumple esta condición.
| 0 | 24 | 18 | 12 | 6 | 30
| | 30 | 6 | 12 | 18 | 24 | 0
| | 0 | 24 | 12 | 18 | 6 | 30 | | 30 | 24 | 12 | 18 | 6 | 0 | | 30 | 6 | 18 | 12 | 24 | 0
| | 0 | 6 | 18 | 12 | 24 | 30
|
| | 1 | 6 | 1 | 6 | 6 | 1
| | 5 | 2 | 5 | 5 | 2 | 2
| | 4 | 3 | 3 | 3 | 4 | 4 | | 3 | 4 | 4 | 4 | 3 | 3 | | 2 | 5 | 2 | 2 | 5 | 5
| | 6 | 1 | 6 | 1 | 1 | 6
|
| | 1 | 30 | 19 | 18 | 12 | 31
| | 35 | 8 | 17 | 23 | 26 | 2
| | 4 | 27 | 15 | 21 | 10 | 34
| | 33 | 28 | 16 | 22 | 9 | 3
| | 32 | 11 | 20 | 14 | 29 | 5
| | 6 | 7 | 24 | 13 | 25 | 36
|
|
A continuación se muestra otro ejemplo de un cuadrado mágico de 6×6 construido de esta manera. Aquí las entradas diagonales están dispuestas de manera diferente. El cuadrado principal se construye volteando el cuadrado de la raíz sobre la diagonal principal. En el segundo cuadrado no se cumple la condición de un solo cuadrado par, lo que conduce a un cuadrado mágico no normal (tercer cuadrado) donde los números 3, 13, 24 y 34 se duplican y faltan los números 4, 18, 19 y 33.
| 6 | 30 | 12 | 18 | 0 | 24
| | 24 | 0 | 12 | 18 | 30 | 6
| | 24 | 0 | 18 | 12 | 30 | 6 | | 6 | 30 | 18 | 12 | 0 | 24 | | 24 | 0 | 18 | 12 | 30 | 6
| | 6 | 30 | 12 | 18 | 0 | 24
|
| | 2 | 5 | 5 | 2 | 5 | 2
| | 6 | 1 | 1 | 6 | 1 | 6
| | 3 | 3 | 4 | 4 | 4 | 3 | | 4 | 4 | 3 | 3 | 3 | 4 | | 1 | 6 | 6 | 1 | 6 | 1
| | 5 | 2 | 2 | 5 | 2 | 5
|
| | 8 | 35 | 17 | 20 | 5 | 26
| | 30 | 1 | 13 | 24 | 31 | 12
| | 27 | 3 | 22 | 16 | 34 | 9
| | 10 | 34 | 21 | 15 | 3 | 28
| | 25 | 6 | 24 | 13 | 36 | 7
| | 11 | 32 | 14 | 23 | 2 | 29
|
|
La última condición es un poco arbitraria y es posible que no siempre sea necesario invocarla, como en este ejemplo, donde en el cuadrado de la raíz cada celda está emparejada verticalmente con su complemento:
| 6 | 30 | 12 | 24 | 18 | 0
| | 6 | 0 | 18 | 24 | 12 | 30
| | 24 | 0 | 12 | 6 | 18 | 30
| | 6 | 30 | 18 | 24 | 12 | 0
| | 24 | 30 | 12 | 6 | 18 | 0
| | 24 | 0 | 18 | 6 | 12 | 30
|
| | 2 | 2 | 5 | 2 | 5 | 5
| | 6 | 1 | 1 | 6 | 6 | 1
| | 3 | 4 | 3 | 4 | 3 | 4
| | 5 | 5 | 2 | 5 | 2 | 2
| | 4 | 3 | 4 | 3 | 4 | 3
| | 1 | 6 | 6 | 1 | 1 | 6
|
| | 8 | 32 | 17 | 26 | 23 | 5
| | 12 | 1 | 19 | 30 | 18 | 31
| | 27 | 4 | 15 | 10 | 21 | 34
| | 11 | 35 | 20 | 29 | 14 | 2
| | 28 | 33 | 16 | 9 | 22 | 3
| | 25 | 6 | 24 | 7 | 13 | 36
|
|
Como ejemplo más, hemos generado un cuadrado mágico de 8×8. A diferencia del patrón entrecruzado de la sección anterior para un cuadrado parejo, aquí tenemos un patrón cuadriculado para las celdas alteradas y no alteradas. Además, en cada cuadrante los números pares e impares aparecen en columnas alternas.
| 0 | 48 | 16 | 32 | 24 | 40 | 8 | 56
| | 56 | 8 | 40 | 24 | 32 | 16 | 48 | 0
| | 0 | 48 | 16 | 32 | 24 | 40 | 8 | 56
| | 56 | 8 | 40 | 24 | 32 | 16 | 48 | 0
| | 56 | 8 | 40 | 24 | 32 | 16 | 48 | 0
| | 0 | 48 | 16 | 32 | 24 | 40 | 8 | 56
| | 56 | 8 | 40 | 24 | 32 | 16 | 48 | 0
| | 0 | 48 | 16 | 32 | 24 | 40 | 8 | 56
|
| | 1 | 8 | 1 | 8 | 8 | 1 | 8 | 1
| | 7 | 2 | 7 | 2 | 2 | 7 | 2 | 7
| | 3 | 6 | 3 | 6 | 6 | 3 | 6 | 3
| | 5 | 4 | 5 | 4 | 4 | 5 | 4 | 5
| | 4 | 5 | 4 | 5 | 5 | 4 | 5 | 4
| | 6 | 3 | 6 | 3 | 3 | 6 | 3 | 6
| | 2 | 7 | 2 | 7 | 7 | 2 | 7 | 2
| | 8 | 1 | 8 | 1 | 1 | 8 | 1 | 8
|
| | 1 | 56 | 17 | 40 | 32 | 41 | 16 | 57
| | 63 | 10 | 47 | 26 | 34 | 23 | 50 | 7
| | 3 | 54 | 19 | 38 | 30 | 43 | 14 | 59
| | 61 | 12 | 45 | 28 | 36 | 21 | 42 | 5
| | 60 | 13 | 44 | 29 | 37 | 20 | 53 | 4
| | 6 | 51 | 22 | 35 | 27 | 46 | 11 | 62
| | 58 | 15 | 42 | 31 | 39 | 18 | 55 | 2
| | 8 | 47 | 24 | 33 | 25 | 48 | 9 | 64
|
|
Variaciones: Son posibles varias variaciones de la idea básica: un par complementario puede aparecer n/2 veces o menos en una columna. Es decir, se puede construir una columna de un cuadrado griego usando más de un par complementario. Este método nos permite imbuir el cuadrado mágico con propiedades mucho más ricas. La idea también se puede extender a las diagonales. A continuación se muestra un ejemplo de un cuadrado mágico de 8 × 8. En el cuadrado terminado, cada uno de los cuatro cuadrantes también son cuadrados panmágicos, cada cuadrante con la misma constante mágica 130.
| 0 | 48 | 56 | 8 | 16 | 32 | 40 | 24
| | 56 | 8 | 0 | 48 | 40 | 24 | 16 | 32
| | 0 | 48 | 56 | 8 | 16 | 32 | 40 | 24
| | 56 | 8 | 0 | 48 | 40 | 24 | 16 | 32
| | 48 | 0 | 8 | 56 | 32 | 16 | 24 | 40
| | 8 | 56 | 48 | 0 | 24 | 40 | 32 | 16
| | 48 | 0 | 8 | 56 | 32 | 16 | 24 | 40
| | 8 | 56 | 48 | 0 | 24 | 40 | 32 | 16
|
| | 1 | 8 | 1 | 8 | 7 | 2 | 7 | 2
| | 7 | 2 | 7 | 2 | 1 | 8 | 1 | 8
| | 8 | 1 | 8 | 1 | 2 | 7 | 2 | 7
| | 2 | 7 | 2 | 7 | 8 | 1 | 8 | 1
| | 3 | 6 | 3 | 6 | 5 | 4 | 5 | 4
| | 5 | 4 | 5 | 4 | 3 | 6 | 3 | 6
| | 6 | 3 | 6 | 3 | 4 | 5 | 4 | 5
| | 4 | 5 | 4 | 5 | 6 | 3 | 6 | 3
|
| | 1 | 56 | 57 | 16 | 23 | 34 | 47 | 26
| | 63 | 10 | 7 | 50 | 41 | 32 | 17 | 40
| | 8 | 49 | 64 | 9 | 18 | 39 | 42 | 31
| | 58 | 15 | 2 | 55 | 48 | 25 | 24 | 33
| | 51 | 6 | 11 | 62 | 37 | 20 | 29 | 44
| | 13 | 60 | 53 | 4 | 27 | 46 | 35 | 22
| | 54 | 3 | 14 | 59 | 36 | 21 | 28 | 45
| | 12 | 61 | 52 | 5 | 30 | 43 | 38 | 19
|
|
Método de bordes
Método de delimitación para el pedido 3
En este método, el objetivo es envolver un borde alrededor de un cuadrado mágico más pequeño que sirve como núcleo. Considere el cuadrado de 3 × 3, por ejemplo. Restando el número medio 5 de cada número 1, 2,..., 9, obtenemos 0, ± 1, ± 2, ± 3 y ± 4, que, a falta de mejores palabras, seguiremos a S. Harry White, se refieren como números de huesos. La constante mágica de un cuadrado mágico, al que nos referiremos como el cuadrado esqueleto, formado por estos números óseos será cero, ya que al sumar todas las filas de un cuadrado mágico se obtendrá nM = Σ k = 0; por lo tanto M = 0.
No es difícil argumentar que el número del medio debe colocarse en la celda del centro: sea x el número colocado en la celda del medio, luego la suma de la columna del medio, la fila del medio, y las dos diagonales dan Σ k + 3 x = 4 M. Como Σ k = 3 M, tenemos x = M / 3. Aquí M = 0, entonces x = 0.
Al colocar el número 0 del medio en la celda central, queremos construir un borde de modo que el cuadrado resultante sea mágico. Sea la frontera dada por:
Dado que la suma de cada fila, columna y diagonales debe ser una constante (que es cero), tenemos
- a + a* = 0,
- b + b) = 0,
- u + U* = 0,
- v + v) = 0.
Ahora, si hemos elegido a, b, u y v, entonces tenemos a* = - a, b* = - b, u* = - u, y v* = - v. Esto significa que si asignamos un número dado a una variable, digamos a = 1, entonces su complemento se asignará a a*, es decir, a* = - 1. Así, de ocho variables desconocidas, es suficiente especificar el valor de solo cuatro variables. Consideraremos a, b, u y v como variables independientes, mientras que a*, b*, u* y v* como variables dependientes. Esto nos permite considerar un número de hueso ± x como un solo número independientemente del signo porque (1) su asignación a una variable dada, digamos a, implicará automáticamente que el mismo número de signo opuesto será compartida con su complemento a*, y (2) a dos variables independientes, digamos a y b, no se les puede asignar el mismo número de hueso. Pero, ¿cómo debemos elegir a, b, u y v? Tenemos la suma de la fila superior y la suma de la columna derecha como
- u + a + v = 0,
- v + b + U* = 0.
Dado que 0 es un número par, solo hay dos formas de que la suma de tres enteros produzca un número par: 1) si los tres fueran pares, o 2) si dos fueran impares y uno par. Dado que en nuestra elección de números solo tenemos dos números pares distintos de cero (± 2 y ± 4), la primera afirmación es falsa. Por lo tanto, debe darse el caso de que la segunda afirmación sea verdadera: que dos de los números sean impares y uno par.
La única forma en que las dos ecuaciones anteriores pueden satisfacer esta condición de paridad simultáneamente, y seguir siendo consistentes con el conjunto de números que tenemos, es cuando u y v son raros Porque, por el contrario, si en la primera ecuación hubiéramos supuesto que u y a eran impares y que v eran pares, entonces u* = - u será impar en la segunda ecuación, haciendo que b también sea impar, para satisfacer la condición de paridad. Pero esto requiere tres números impares (u, a y b), lo que contradice el hecho de que solo tenemos dos números impares (± 1 y ± 3) que podemos usar. Esto prueba que los números impares de huesos ocupan las celdas de las esquinas. Cuando se convierte a números normales sumando 5, esto implica que las esquinas de un cuadrado mágico de 3×3 están ocupadas por números pares.
Así, tomando u = 1 y v = 3, tenemos a = - 4 y b = - 2. Por lo tanto, el cuadrado del esqueleto terminado será como el de la izquierda. Sumando 5 a cada número, obtenemos el cuadrado mágico terminado.
Se puede usar un argumento similar para construir cuadrados más grandes. Dado que no existe un cuadrado mágico de 2×2 alrededor del cual podamos envolver un borde para construir un cuadrado mágico de 4×4, el siguiente orden más pequeño para el que podemos construir un cuadrado bordeado es el orden 5.
Método de delimitación para el pedido 5
Considere el cuadrado de quinto orden. Para esto, tenemos un núcleo mágico de 3×3, alrededor del cual envolveremos un borde mágico. Los números de huesos a utilizar serán ± 5, ± 6, ± 7, ± 8, ± 9, ± 10, ± 11 y ± 12. Despreciando los signos tenemos 8 números de huesos, 4 de los cuales son pares y 4 de los cuales son impares. En general, para un cuadrado de cualquier orden n, habrá 4(n - 1) celdas de borde, que se rellenarán con 2(n - 1) número de huesos. Deje que el borde mágico se dé como
| u | a | b | c | v
|
| d) | | | | d
|
| e) | | | | e
|
| f) | | | | f
|
| v) | a* | b) | c) | U*
|
Como antes, debemos
- colocar un número de hueso y su complemento opuesto al otro, para que la suma mágica sea cero.
Es suficiente determinar los números u, v, a, b, c, d, e, f para describir el borde mágico. Como antes, tenemos las dos ecuaciones de restricción para la fila superior y la columna derecha:
- u + a + b + c + v = 0
- v + d + e + f + U* = 0.
Hay varias soluciones posibles. El procedimiento estándar es para
- primero tratar de determinar las células de la esquina, después de lo cual intentaremos determinar el resto de la frontera.
Hay 28 formas de elegir dos números del conjunto de 8 números óseos para las celdas de las esquinas u y v. Sin embargo, no todos los pares son admisibles. Entre los 28 pares, 16 pares están formados por un número par y un impar, 6 pares tienen ambos números pares, mientras que 6 pares tienen ambos números impares.
Podemos demostrar que las celdas de las esquinas u y v no pueden tener un número par e impar. Esto se debe a que si esto fuera así, entonces las sumas u + v y v + u* serán impares, y dado que 0 es un número par, las sumas a + b + c y d + e + f también debería ser impar. La única forma en que la suma de tres números enteros dará como resultado un número impar es cuando 1) dos de ellos son pares y uno es impar, o 2) cuando los tres son impares. Dado que se supone que las celdas de las esquinas son pares e impares, ninguna de estas dos afirmaciones es compatible con el hecho de que solo tenemos a nuestra disposición 3 números de huesos pares y 3 impares. Esto prueba que u y v no pueden tener paridad diferente. Esto elimina 16 posibilidades.
Usando un razonamiento de tipo similar también podemos sacar algunas conclusiones sobre los conjuntos {a, b, c} y {d , e, f}. Si u y v son pares, ambos conjuntos deben tener dos números impares y un número par. Si tanto u como v son impares, entonces uno de los conjuntos debe tener tres números pares mientras que el otro conjunto debe tener un número par y dos números impares.
Como ejemplo, considere el caso en el que tanto u como v son pares. Los 6 pares posibles son: (6, 8), (6, 10), (6, 12), (8, 10), (8, 12) y (10, 12). Dado que las sumas u + v y v + u* son pares, las sumas a + b + c y d + e + f deben ser pares también. La única manera de que la suma de tres enteros resulte en un número par es cuando 1) dos de ellos son impares y uno es par, o 2) cuando los tres son pares. El hecho de que las dos celdas de las esquinas sean pares significa que solo tenemos 2 números pares a nuestra disposición. Por lo tanto, la segunda afirmación no es compatible con este hecho. Por lo tanto, debe darse el caso de que la primera afirmación sea verdadera: dos de los tres números deben ser impares, mientras que uno debe ser par.
Ahora, sean a, b, d, e números impares mientras que c y f sean números pares. Dados los números de huesos impares a nuestra disposición: ± 5, ± 7, ± 9 y ± 11, sus diferencias van desde D = { ± 2, ± 4, ± 6} mientras que sus sumas van desde S = {± 12, ± 14, ± 16, ± 18, ± 20}. También es útil tener una tabla de su suma y diferencia para referencia posterior. Ahora, dadas las celdas de las esquinas (u, v), podemos comprobar su admisibilidad comprobando si las sumas u + v + c y v + u* + f caen dentro del conjunto D o S. La admisibilidad de los números de esquina es una condición necesaria pero no suficiente para que exista la solución.
Por ejemplo, si consideramos el par (u, v) = (8, 12), entonces u + v = 20 y v + u* = 6; y tendremos a nuestra disposición ± 6 y ± 10 números pares de huesos. Tomando c = ± 6, tenemos que la suma u + v + c es 26 y 14, dependiendo en el signo de ± 6 tomado, los cuales no caen dentro de los conjuntos D o S. Asimismo, tomando c = ± 10, tenemos que la suma u + v + c es 30 y 10, los cuales de nuevo no caen dentro de los conjuntos D o S. Por lo tanto, el par (8, 12) no es admisible. Mediante un proceso de razonamiento similar, también podemos descartar el par (6, 12).
Como otro ejemplo, si consideramos el par (u, v) = (10, 12), entonces u + v = 22 y v + u* = 2; y tendremos ± 6 y ± 8 números pares de huesos a nuestra disposición. Tomando c = ± 6, tenemos la suma de u + v + c como 28 y 16. Mientras que 28 no cae dentro de los conjuntos D o S, 16 cae en el conjunto S. Por inspección, encontramos que si (a, b) = (-7, -9), entonces a + b = -16; y satisfará la primera ecuación de restricción. Además, tomando f = ± 8, tenemos que la suma v + u* + f es 10 y -6. Mientras que 10 no cae dentro de los conjuntos D o S, -6 cae en el conjunto D. Dado que -7 y -9 ya se han asignado a a y b, claramente (d, e) = (-5, 11) de modo que d + e = 6; y satisfará la segunda ecuación de restricción.
Del mismo modo, tomando c = ± 8, tenemos la suma u + v + c para ser 30 y 14. Mientras que 30 no cae dentro de los conjuntos D o S, 14 cae en el conjunto S. Por inspección, encontramos que si (a, b) = (-5, -9), entonces a + b = -14. Además, tomando f = ± 6, tenemos que la suma v + u* + f es 8 y -4. Mientras que 8 no cae dentro de los conjuntos D o S, -4 cae en el conjunto D. Claramente, (d, e) = (-7, 11) de modo que d + e = 4, y se satisfará la segunda ecuación de restricción.
Por lo tanto, el par de esquinas (u, v) = (10, 12) es admisible; y admite dos soluciones: (a, b, c, d, e, f) = (-7, -9, -6, -5, 11, -8) y (a, b, c, d, e, f) = (-5, -9, -8, -7, 11, -6). Los cuadrados de esqueleto terminados se dan a continuación. El cuadrado mágico se obtiene sumando 13 a cada celda.
| 10 | -7 | -9 | -6 | 12
| | 5 | | | | -5
| | -11 | | | | 11
| | 8 | | | | -8
| | -12 | 7 | 9 | 6 | -10
|
| | 23 | 6 | 4 | 7 | 25
| | 18 | | | | 8
| | 2 | | | | 24
| | 21 | | | | 5
| | 1 | 20 | 22 | 19 | 3
|
| | 10 | -5 | -9 | -8 | 12
| | 7 | | | | -7
| | -11 | | | | 11
| | 6 | | | | -6
| | -12 | 5 | 9 | 8 | -10
|
| | 23 | 8 | 4 | 5 | 25
| | 20 | | | | 6
| | 2 | | | | 24
| | 19 | | | | 7
| | 1 | 18 | 22 | 21 | 3
|
|
Usando un proceso de razonamiento similar, podemos construir la siguiente tabla para los valores de u, v, a, b, c, d, e, f expresados como números de huesos como se indica a continuación. Solo hay 6 opciones posibles para las celdas de las esquinas, lo que lleva a 10 posibles soluciones de borde.
| u, v | a, b, c | d, e, f |
|---|
| 12, 10 | -6, 7, 9 | -11, 5, 8
|
| 12, 10 | -5, -8, -9 | -11, 6, 7
|
| 11, 5 | 6, 10, 12 | -9, 7, 8
|
| 10, 6 | 5, -9, -12 | -11, 7, 8
|
| 10, 6 | 7, 11 -12 | -9, 5, 8
|
| 9, 7 | 5, -10, -11 | -12, 6, 8
|
| 9, 7 | 6, 10, 12 | -11, 5, 8
|
| 8, 6 | 7, 10, 11 | -12, 5, 9
|
| 8, 6 | 9, 11 -12 | -10, 5, 7
|
| 7, 5 | 9, 10, 11 | -12, 6, 8
|
Dado este grupo de 10 bordes, podemos construir 10×8×(3!)2 = 2880 cuadrados mágicos con bordes esencialmente diferentes. Aquí los números de hueso ± 5,..., ± 12 eran consecutivos. Se pueden construir más cuadrados bordeados si los números no son consecutivos. Si también se usaron números de huesos no consecutivos, entonces hay un total de 605 bordes mágicos. Por lo tanto, el número total de cuadrados mágicos bordeados esencialmente diferentes de orden 5 (con números consecutivos y no consecutivos) es 174.240. Ver historia. Vale la pena señalar que la cantidad de cuadrados mágicos de quinto orden que se pueden construir mediante el método de bordes es aproximadamente 26 veces mayor que mediante el método de superposición.
Métodos de enumeración continua
La enumeración exhaustiva de todos los bordes de un cuadrado mágico de un orden determinado, como se hacía anteriormente, es muy tediosa. Como tal, a menudo es deseable una solución estructurada que nos permita construir un borde para un cuadrado de cualquier orden. A continuación damos tres algoritmos para construir bordes para cuadrados impares, doblemente pares y pares individuales. Estos algoritmos de enumeración continua fueron descubiertos en el siglo X por eruditos árabes; y su exposición más antigua que se conserva proviene de los dos tratados de al-Buzjani y al-Antaki, aunque ellos mismos no fueron los descubridores. Desde entonces, se han descubierto muchos más algoritmos de este tipo.
Cuadrados ordenados impares: El siguiente es el algoritmo dado por al-Buzjani para construir un borde para cuadrados impares. Una peculiaridad de este método es que para el cuadrado de orden n, las dos esquinas adyacentes son los números n - 1 y n + 1.
Comenzando desde la celda arriba de la esquina inferior izquierda, colocamos los números alternativamente en la columna izquierda y en la fila inferior hasta llegar a la celda del medio. El siguiente número se escribe en la celda del medio de la fila inferior recién alcanzada, después de lo cual llenamos la celda en la esquina superior izquierda, luego la celda del medio de la columna derecha, luego la esquina superior derecha. Después de esto, comenzando desde la celda arriba de la celda central de la columna derecha ya llena, retomamos la ubicación alternativa de los números en la columna derecha y la fila superior. Una vez que se llena la mitad de las celdas del borde, la otra mitad se llena con números complementarios a las celdas opuestas. Los bordes interiores subsiguientes se rellenan de la misma manera, hasta que se rellena el cuadrado de orden 3.
A continuación se muestra un ejemplo de cuadrado de noveno orden.
| 8 | 80 | 78 | 76 | 75 | 12 | 14 | 16 | 10 |
| 67 | 22 | 64 | 62 | 61 | 26 | 28 | 24 | 15 |
| 69 | 55 | 32 | 52 | 51 | 36 | 34 | 27 | 13 |
| 71 | 57 | 47 | 38 | 45 | 40 | 35 | 25 | 11 |
| 73 | 59 | 49 | 43 | 41 | 39 | 33 | 23 | 9 |
| 5 | 19 | 29 | 42 | 37 | 44 | 53 | 63 | 77
|
| 3 | 17 | 48 | 30 | 31 | 46 | 50 | 65 | 79
|
| 1 | 58 | 18 | 20 | 21 | 56 | 54 | 60 | 81
|
| 72 | 2 | 4 | 6 | 7 | 70 | 68 | 66 | 74
|
Orden doblemente uniforme: El siguiente es el método dado por al-Antaki. Considere un borde vacío de orden n = 4k con k ≥ 3. La peculiaridad de este algoritmo es que las celdas de las esquinas adyacentes están ocupadas por números n y n - 1.
Comenzando en la celda de la esquina superior izquierda, ponemos los números sucesivos por grupos de cuatro, el primero junto a la esquina, el segundo y el tercero en la parte inferior, y el cuarto en la parte superior, y así hasta allí permanece en la fila superior (excluyendo las esquinas) seis celdas vacías. Luego escribimos los siguientes dos números arriba y los siguientes cuatro abajo. Luego rellenamos las esquinas superiores, primero a la izquierda y luego a la derecha. Colocamos el siguiente número debajo de la esquina superior derecha en la columna de la derecha, el siguiente número del otro lado en la columna de la izquierda. Luego retomamos la colocación de grupos de cuatro números consecutivos en las dos columnas como antes. Una vez que se llena la mitad de las celdas del borde, la otra mitad se llena con números complementarios a las celdas opuestas.
El siguiente ejemplo muestra el borde para el cuadrado de orden 16.
| 15 | 1 | 255 | 254 | 4 | 5 | 251 | 250 | 8 | 9 | 10 | 246 | 245 | 244 | 243 | 16 |
| 240 | | | | | | | | | | | | | | | 17 |
| 18 | | | | | | | | | | | | | | | 239
|
| 19 | | | | | | | | | | | | | | | 238
|
| 237 | | | | | | | | | | | | | | | 20 |
| 236 | | | | | | | | | | | | | | | 21 |
| 22 | | | | | | | | | | | | | | | 235
|
| 23 | | | | | | | | | | | | | | | 234
|
| 233 | | | | | | | | | | | | | | | 24 |
| 232 | | | | | | | | | | | | | | | 25 |
| 26 | | | | | | | | | | | | | | | 231
|
| 27 | | | | | | | | | | | | | | | 230
|
| 229 | | | | | | | | | | | | | | | 28 |
| 228 | | | | | | | | | | | | | | | 29 |
| 30 | | | | | | | | | | | | | | | 227
|
| 241 | 256 | 2 | 3 | 253 | 252 | 6 | 7 | 249 | 248 | 247 | 11 | 12 | 13 | 14 | 242
|
Para el cuadrado de orden 8, comenzamos directamente con las seis celdas.
| 7 | 1 | 2 | 62 | 61 | 60 | 59 | 8 |
| 56 | | | | | | | 9 |
| 10 | | | | | | | 55
|
| 11 | | | | | | | 54
|
| 53 | | | | | | | 12 |
| 52 | | | | | | | 13 |
| 14 | | | | | | | 51
|
| 57 | 64 | 63 | 3 | 4 | 5 | 6 | 58
|
Orden paritario: Para orden paritario tenemos el algoritmo dado por al-Antaki. Aquí las celdas de las esquinas están ocupadas por n y n - 1. A continuación se muestra un ejemplo de cuadrado de décimo orden.
Comience colocando 1 en la fila inferior junto a la celda de la esquina izquierda, luego coloque 2 en la fila superior. Después de esto, coloque 3 en la fila inferior y gire alrededor del borde en sentido contrario a las agujas del reloj colocando los siguientes números, hasta llegar a n - 2 en la columna de la derecha. Los siguientes dos números se colocan en las esquinas superiores (n - 1 en la esquina superior izquierda y n en la esquina superior derecha). Luego, los siguientes dos números se colocan en la columna de la izquierda, luego reanudamos la colocación cíclica de los números hasta que se llena la mitad de todas las celdas del borde. Una vez que se llena la mitad de las celdas del borde, la otra mitad se llena con números complementarios a las celdas opuestas.
| 9 | 100 | 2 | 98 | 5 | 94 | 88 | 15 | 84 | 10 |
| 83 | | | | | | | | | 18 |
| 16 | | | | | | | | | 85
|
| 87 | | | | | | | | | 14 |
| 12 | | | | | | | | | 89
|
| 11 | | | | | | | | | 90
|
| 93 | | | | | | | | | 8 |
| 6 | | | | | | | | | 95
|
| 97 | | | | | | | | | 4 |
| 91 | 1 | 99 | 3 | 96 | 7 | 13 | 86 | 17 | 92
|
Método de composición
Para cuadrados de orden m × n donde m, n > 2
Este es un método que recuerda al producto de Kronecker de dos matrices, que construye un cuadrado mágico nm × nm a partir de un n × n cuadrado mágico y un cuadrado mágico m × m. El "producto" de dos cuadrados mágicos crea un cuadrado mágico de mayor orden que los dos multiplicandos. Sean los dos cuadrados mágicos de orden m y n. El cuadrado final será de orden m × n. Divida el cuadrado de orden m × n en subcuadrados m × m, de modo que haya un total de n2 tales subcuadrados. En el cuadrado de orden n, reduce en 1 el valor de todos los números. Multiplique estos valores reducidos por m2 y coloque los resultados en los subcuadrados correspondientes del cuadrado entero m × n. Los cuadrados de orden m se suman n2 veces a los subcuadrados del cuadrado final. La peculiaridad de este método de construcción es que cada subcuadrado mágico tendrá distintas sumas mágicas. El cuadrado formado por tales sumas mágicas de cada subcuadrado mágico volverá a ser un cuadrado mágico. El cuadrado mágico compuesto más pequeño de orden 9, compuesto por dos cuadrados de orden 3, se muestra a continuación.
| Orden 3×3
| 63 | 63 | 63 | 0 | 0 | 0 | 45 | 45 | 45
| | 63 | 63 | 63 | 0 | 0 | 0 | 45 | 45 | 45
| | 63 | 63 | 63 | 0 | 0 | 0 | 45 | 45 | 45
| | 18 | 18 | 18 | 36 | 36 | 36 | 54 | 54 | 54
| | 18 | 18 | 18 | 36 | 36 | 36 | 54 | 54 | 54
| | 18 | 18 | 18 | 36 | 36 | 36 | 54 | 54 | 54
| | 27 | 27 | 27 | 72 | 72 | 72 | 9 | 9 | 9
| | 27 | 27 | 27 | 72 | 72 | 72 | 9 | 9 | 9
| | 27 | 27 | 27 | 72 | 72 | 72 | 9 | 9 | 9
|
| Orden 3×3
| 71 | 64 | 69 | 8 | 1 | 6 | 53 | 46 | 51
| | 66 | 68 | 70 | 3 | 5 | 7 | 48 | 50 | 52
| | 67 | 72 | 65 | 4 | 9 | 2 | 49 | 54 | 47
| | 26 | 19 | 24 | 44 | 37 | 42 | 62 | 55 | 60
| | 21 | 23 | 25 | 39 | 41 | 43 | 57 | 59 | 61
| | 22 | 27 | 20 | 40 | 45 | 38 | 58 | 63 | 56
| | 35 | 28 | 33 | 80 | 73 | 78 | 17 | 10 | 15
| | 30 | 32 | 34 | 75 | 77 | 79 | 12 | 14 | 16
| | 31 | 36 | 29 | 76 | 81 | 74 | 13 | 18 | 11
| |
Dado que cada uno de los subcuadrados de 3×3 se puede rotar de forma independiente y reflejarse en 8 cuadrados diferentes, a partir de este único cuadrado compuesto de 9×9 podemos derivar 89 = 134 217 728 9× esencialmente diferentes 9 cuadrados compuestos. También se pueden derivar muchos más cuadrados mágicos compuestos si seleccionamos números no consecutivos en los subcuadrados mágicos, como en la versión de Yang Hui del cuadrado mágico compuesto 9×9. Los siguientes cuadrados mágicos compuestos más pequeños de orden 12, compuestos por cuadrados mágicos de orden 3 y 4 se dan a continuación.
| Orden No 4
| 1 | 14 | 11 | 8
| | 12 | 7 | 2 | 13
| | 6 | 9 | 16 | 3
| | 15 | 4 | 5 | 10
|
| Orden 3 × 4
| 2 | 9 | 4 | 119 | 126 | 121 | 92 | 99 | 94 | 65 | 72 | 67
| | 7 | 5 | 3 | 124 | 122 | 120 | 97 | 95 | 93 | 70 | 68 | 66
| | 6 | 1 | 8 | 123 | 118 | 125 | 96 | 91 | 98 | 69 | 64 | 71
| | 101 | 108 | 103 | 56 | 63 | 58 | 11 | 18 | 13 | 110 | 117 | 112
| | 106 | 104 | 102 | 61 | 59 | 57 | 16 | 14 | 12 | 115 | 113 | 111
| | 105 | 100 | 107 | 60 | 55 | 62 | 15 | 10 | 17 | 114 | 109 | 116
| | 47 | 54 | 49 | 74 | 81 | 76 | 137 | 144 | 139 | 20 | 27 | 22
| | 52 | 50 | 48 | 79 | 77 | 75 | 142 | 140 | 138 | 25 | 23 | 21
| | 51 | 46 | 53 | 78 | 73 | 80 | 141 | 136 | 143 | 24 | 19 | 26
| | 128 | 135 | 130 | 29 | 36 | 31 | 38 | 45 | 40 | 83 | 90 | 85
| | 133 | 131 | 129 | 34 | 32 | 30 | 43 | 41 | 39 | 88 | 86 | 84
| | 132 | 127 | 134 | 33 | 28 | 35 | 42 | 37 | 44 | 87 | 82 | 89
|
| Orden 4 × 3
| 17 | 30 | 27 | 24 | 129 | 142 | 139 | 136 | 49 | 62 | 59 | 56
| | 28 | 23 | 18 | 29 | 140 | 135 | 130 | 141 | 60 | 55 | 50 | 61
| | 22 | 25 | 32 | 19 | 134 | 137 | 144 | 131 | 54 | 57 | 64 | 51
| | 31 | 20 | 21 | 26 | 143 | 132 | 133 | 138 | 63 | 52 | 53 | 58
| | 97 | 110 | 107 | 104 | 65 | 78 | 75 | 72 | 33 | 46 | 43 | 40
| | 108 | 103 | 98 | 109 | 76 | 71 | 66 | 77 | 44 | 39 | 34 | 45
| | 102 | 105 | 112 | 99 | 70 | 73 | 80 | 67 | 38 | 41 | 48 | 35
| | 111 | 100 | 101 | 106 | 79 | 68 | 69 | 74 | 47 | 36 | 37 | 42
| | 81 | 94 | 91 | 88 | 1 | 14 | 11 | 8 | 113 | 126 | 123 | 120
| | 92 | 87 | 82 | 93 | 12 | 7 | 2 | 13 | 124 | 119 | 114 | 125
| | 86 | 89 | 96 | 83 | 6 | 9 | 16 | 3 | 118 | 121 | 128 | 115
| | 95 | 84 | 85 | 90 | 15 | 4 | 5 | 10 | 127 | 116 | 117 | 122
| |
Para los cuadrados base, solo hay un cuadrado de tercer orden esencialmente diferente, mientras que hay 880 cuadrados de cuarto orden esencialmente diferentes entre los que podemos elegir. Cada emparejamiento puede producir dos cuadrados compuestos diferentes. Dado que cada subcuadrado mágico en cada cuadrado compuesto se puede expresar en 8 formas diferentes debido a rotaciones y reflejos, puede haber 1×880×89 + 880×1×816 ≈ 2.476×1017 cuadrados mágicos compuestos de 12×12 esencialmente diferentes creados de esta manera, con números consecutivos en cada subcuadrado. En general, si hay cm y cn cuadrados mágicos esencialmente diferentes de orden m y n, entonces podemos formar cm × cn × (8m2 + 8n2) cuadrados compuestos de orden mn, siempre que m ≠ n. Si m = n, entonces podemos formar (cm)2 × 8m2 cuadrados compuestos de orden m2.
Para cuadrados de orden doblemente par
Cuando los cuadrados son de doble orden, podemos construir un cuadrado mágico compuesto de una manera más elegante que el proceso anterior, en el sentido de que cada subcuare mágico tendrá la misma constante mágica. Vamos n ser el orden de la plaza principal y m el orden de los subsquares iguales. Los subsquares se llenan uno por uno, en cualquier orden, con una secuencia continua de m2/2 números más pequeños (es decir, números inferiores o iguales a n2/2) junto con sus complementos a n2 + 1. Cada subsquare como un todo dará la misma suma mágica. La ventaja de este tipo de cuadrado compuesto es que cada subsquare se llena de la misma manera y su arreglo es arbitrario. Así, el conocimiento de una sola construcción de incluso orden será suficiente para llenar toda la plaza. Además, si los subsquares se llenan en la secuencia natural, entonces el cuadrado resultante será pandiagonal. La suma mágica de los submarinos está relacionada con la suma mágica de toda la plaza por Mm=Mnk{displaystyle M_{m}={frac {fn} {fn}}} {fn}}} {fn}}}}} {fn}}}}}} {fn}}}}}} {fn}}}}}}}}}}} {fn}} {}}}}}}}}}}} {cH}}}} {}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} Donde n = km.
Donde n = km.
En los ejemplos a continuación, hemos dividido el cuadrado de orden 12 en nueve subcuadrados de orden 4 rellenos cada uno con ocho números más pequeños y, en las celdas correspondientes al obispo (dos celdas en diagonal, incluidos los círculos, en el 4×4 subcuadrado), sus complementos a n2 + 1 = 145. Cada subcuadrado es pandiagonal con constante mágica 290; mientras que todo el cuadrado de la izquierda también es pandiagonal con constante mágica 870.
| 1 | 142 | 139 | 8 | 9 | 134 | 131 | 16 | 17 | 126 | 123 | 24 | | 140 | 7 | 2 | 141 | 132 | 15 | 10 | 133 | 124 | 23 | 18 | 125
| | 6 | 137 | 144 | 3 | 14 | 129 | 136 | 11 | 22 | 121 | 128 | 19 | | 143 | 4 | 5 | 138 | 135 | 12 | 13 | 130 | 127 | 20 | 21 | 122
| | 25 | 118 | 115 | 32 | 33 | 110 | 107 | 40 | 41 | 102 | 99 | 48 | | 116 | 31 | 26 | 117 | 108 | 39 | 34 | 109 | 100 | 47 | 42 | 101
| | 30 | 113 | 120 | 27 | 38 | 105 | 112 | 35 | 46 | 97 | 104 | 43 | | 119 | 28 | 29 | 114 | 111 | 36 | 37 | 106 | 103 | 44 | 45 | 98
| | 49 | 94 | 91 | 56 | 57 | 86 | 83 | 64 | 65 | 78 | 75 | 72 | | 92 | 55 | 50 | 93 | 84 | 63 | 58 | 85 | 76 | 71 | 66 | 77
| | 54 | 89 | 96 | 51 | 62 | 81 | 88 | 59 | 70 | 73 | 80 | 67 | | 95 | 52 | 53 | 90 | 87 | 60 | 61 | 82 | 79 | 68 | 69 | 74
|
| | 69 | 74 | 79 | 68 | 29 | 114 | 119 | 28 | 61 | 82 | 87 | 60 | | 75 | 72 | 65 | 78 | 115 | 32 | 25 | 118 | 83 | 64 | 57 | 86
| | 66 | 77 | 76 | 71 | 26 | 117 | 116 | 31 | 58 | 85 | 84 | 63 | | 80 | 67 | 70 | 73 | 120 | 27 | 30 | 113 | 88 | 59 | 62 | 81
| | 21 | 122 | 127 | 20 | 53 | 90 | 95 | 52 | 13 | 130 | 135 | 12 | | 123 | 24 | 17 | 126 | 91 | 56 | 49 | 94 | 131 | 16 | 9 | 134
| | 18 | 125 | 124 | 23 | 50 | 93 | 92 | 55 | 10 | 133 | 132 | 15 | | 128 | 19 | 22 | 121 | 96 | 51 | 54 | 89 | 136 | 11 | 14 | 129
| | 45 | 98 | 103 | 44 | 5 | 138 | 143 | 4 | 37 | 106 | 111 | 36 | | 99 | 48 | 41 | 102 | 139 | 8 | 1 | 142 | 107 | 40 | 33 | 110
| | 42 | 101 | 100 | 47 | 2 | 141 | 140 | 7 | 34 | 109 | 108 | 39 | | 104 | 43 | 46 | 97 | 144 | 3 | 6 | 137 | 112 | 35 | 38 | 105
|
|
En otro ejemplo a continuación, hemos dividido el cuadrado de orden 12 en cuatro cuadrados de orden 6. Cada uno de los cuadrados de orden 6 se llena con dieciocho números pequeños y sus complementos utilizando la técnica de bordes dada por al-Antaki. Si eliminamos los bordes sombreados de los subcuadrados de orden 6 y formamos un cuadrado de orden 8, entonces este cuadrado de orden 8 vuelve a ser un cuadrado mágico. En toda su generalidad, podemos tomar cualquier m2/2 números menores junto con sus complementos a n2 + 1 para llenar los subcuadrados, no necesariamente en secuencia continua.
| 60 | 82 | 88 | 56 | 90 | 59 | 24 | 118 | 124 | 20 | 126 | 23 |
| 64 | 69 | 74 | 79 | 68 | 81 | 28 | 33 | 110 | 115 | 32 | 117
|
| 83 | 75 | 72 | 65 | 78 | 62 | 119 | 111 | 36 | 29 | 114 | 26 |
| 84 | 66 | 77 | 76 | 71 | 61 | 120 | 30 | 113 | 112 | 35 | 25 |
| 58 | 80 | 67 | 70 | 73 | 87 | 22 | 116 | 31 | 34 | 109 | 123
|
| 86 | 63 | 57 | 89 | 55 | 85 | 122 | 27 | 21 | 125 | 19 | 121
|
| 6 | 136 | 142 | 2 | 144 | 5 | 42 | 100 | 106 | 38 | 108 | 41 |
| 10 | 15 | 128 | 133 | 14 | 135 | 46 | 51 | 92 | 97 | 50 | 99
|
| 137 | 129 | 18 | 11 | 132 | 8 | 101 | 93 | 54 | 47 | 96 | 44 |
| 138 | 12 | 131 | 130 | 17 | 7 | 102 | 48 | 95 | 94 | 53 | 43 |
| 4 | 134 | 13 | 16 | 127 | 141 | 40 | 98 | 49 | 52 | 91 | 105
|
| 140 | 9 | 3 | 143 | 1 | 139 | 104 | 45 | 39 | 107 | 37 | 103
|
Método de Medjig para cuadrados de orden par 2n, donde n > 2
Con este método, se "multiplica" un cuadrado mágico. con un cuadrado medjig para crear un cuadrado mágico más grande. El nombre de este método deriva del juego matemático llamado medjig creado por Willem Barink en 2006, aunque el método en sí es mucho más antiguo. Una instancia temprana de un cuadrado mágico construido usando este método ocurre en el texto de Yang Hui para el cuadrado mágico de orden 6. El método LUX para construir cuadrados mágicos pares de forma individual es un caso especial del método medjig, en el que solo se utilizan 3 de los 24 patrones para construir el cuadrado medjig.
Las piezas del rompecabezas medjig son cuadrados de 2×2 en los que se colocan los números 0, 1, 2 y 3. Hay tres patrones básicos mediante los cuales los números 0, 1, 2 y 3 se pueden colocar en un cuadrado de 2×2, donde el 0 está en la esquina superior izquierda:
Cada patrón se puede reflejar y rotar para obtener 8 patrones equivalentes, lo que nos da un total de 3×8 = 24 patrones. El objetivo del rompecabezas es tomar n2 piezas de medjig y colocarlas en un n × n cuadrado medjig de tal manera que cada fila, columna, junto con las dos diagonales largas, formadas por el cuadrado medjig suman 3n, la constante mágica del cuadrado medjig. Un cuadrado medjig n × n puede crear un cuadrado mágico de 2n × 2n donde n > 2.
Dado un cuadrado medjig n×n y una base de cuadrado mágico n×n, un cuadrado mágico de orden 2n×2n se puede construir de la siguiente manera:
- Cada célula de una n×n cuadrado mágico se asocia con un subsquare 2×2 correspondiente del cuadrado de medjig
- Llenar cada subsquares 2×2 de la plaza de medjig con los cuatro números de 1 a 4n2 que iguala el modulo número original n2, es decir. x+n2Sí. Donde x es el número correspondiente de la plaza mágica y Sí. es un número de 0 a 3 en los subsquares 2×2.
Suponiendo que tenemos una base de cuadrado mágico inicial, el desafío radica en construir un cuadrado medjig. Como referencia, las sumas de cada pieza medjig a lo largo de las filas, columnas y diagonales, indicadas en cursiva, son:
Cuadrados doblemente pares: El cuadrado medjig par ordenado más pequeño es de orden 2 con constante mágica 6. Si bien es posible construir un cuadrado medjig de 2×2, no podemos construir un cuadrado medjig de 4×4. cuadrado de él ya que se requieren 2 × 2 cuadrados mágicos para "multiplicar" no existe. Sin embargo, vale la pena construir estos cuadrados medjig de 2×2. La constante mágica 6 se puede dividir en dos partes de tres maneras como 6 = 5 + 1 = 4 + 2 = 3 + 3. Existen 96 cuadrados medjig de 2 × 2. En los ejemplos a continuación, cada cuadrado medjig de 2 × 2 se fabrica combinando diferentes orientaciones de una sola pieza medjig.
Medjig 2×2
| 0 | 1 | 3 | 2
| | 2 | 3 | 1 | 0
| | 3 | 2 | 0 | 1
| | 1 | 0 | 2 | 3
| | Medjig 2×2
| 0 | 1 | 2 | 3
| | 3 | 2 | 1 | 0
| | 1 | 0 | 3 | 2
| | 2 | 3 | 0 | 1
| | Medjig 2×2
| 0 | 2 | 3 | 1
| | 3 | 1 | 0 | 2
| | 0 | 2 | 3 | 1
| | 3 | 1 | 0 | 2
| |
Podemos usar los cuadrados medjig de 2×2 para construir cuadrados medjig más grandes incluso ordenados. Un enfoque posible es simplemente combinar los cuadrados medjig de 2×2. Otra posibilidad es envolver un núcleo cuadrado medjig más pequeño con un borde medjig. Las piezas de un cuadrado medjig de 2×2 pueden formar las esquinas del borde. Otra posibilidad más es agregar una fila y una columna a un cuadrado medjig ordenado impar. Un ejemplo de un cuadrado mágico de 8 × 8 se construye a continuación combinando cuatro copias del cuadrado medjig de 2 × 2 más a la izquierda que se muestra arriba:
Orden No 4
| 1 | 14 | 4 | 15
| | 8 | 11 | 5 | 10
| | 13 | 2 | 16 | 3
| | 12 | 7 | 9 | 6
| | Medjig 4 × 4
| 0 | 1 | 3 | 2 | 0 | 1 | 3 | 2
| | 2 | 3 | 1 | 0 | 2 | 3 | 1 | 0
| | 3 | 2 | 0 | 1 | 3 | 2 | 0 | 1
| | 1 | 0 | 2 | 3 | 1 | 0 | 2 | 3
| | 0 | 1 | 3 | 2 | 0 | 1 | 3 | 2
| | 2 | 3 | 1 | 0 | 2 | 3 | 1 | 0
| | 3 | 2 | 0 | 1 | 3 | 2 | 0 | 1
| | 1 | 0 | 2 | 3 | 1 | 0 | 2 | 3
| | Orden 8
| 1 | 17 | 62 | 46 | 4 | 20 | 63 | 47
| | 33 | 49 | 30 | 14 | 36 | 52 | 31 | 15 | | 56 | 40 | 11 | 27 | 53 | 37 | 10 | 26
| | 24 | 8 | 43 | 59 | 21 | 5 | 42 | 58
| | 13 | 29 | 50 | 34 | 16 | 32 | 51 | 35
| | 45 | 61 | 18 | 2 | 48 | 64 | 19 | 3 | | 60 | 44 | 7 | 23 | 57 | 41 | 6 | 22
| | 28 | 12 | 39 | 55 | 25 | 9 | 38 | 54
| |
El siguiente ejemplo se construye bordeando un núcleo cuadrado medjig de 2×2.
Orden No 4
| 1 | 14 | 4 | 15
| | 8 | 11 | 5 | 10
| | 13 | 2 | 16 | 3
| | 12 | 7 | 9 | 6
| | Medjig 4 × 4
| 0 | 1 | 0 | 1 | 2 | 3 | 3 | 2
| | 2 | 3 | 3 | 2 | 1 | 0 | 1 | 0
| | 0 | 3 | 0 | 2 | 3 | 1 | 0 | 3
| | 1 | 2 | 3 | 1 | 0 | 2 | 1 | 2
| | 2 | 1 | 0 | 2 | 3 | 1 | 2 | 1
| | 3 | 0 | 3 | 1 | 0 | 2 | 3 | 0
| | 3 | 2 | 0 | 1 | 2 | 3 | 0 | 1
| | 1 | 0 | 3 | 2 | 1 | 0 | 2 | 3
| | Orden 8
| 1 | 17 | 14 | 30 | 36 | 52 | 63 | 47
| | 33 | 49 | 62 | 46 | 20 | 4 | 31 | 15 | | 8 | 56 | 11 | 43 | 53 | 21 | 10 | 58
| | 24 | 40 | 59 | 27 | 5 | 37 | 26 | 42
| | 45 | 29 | 2 | 34 | 64 | 32 | 35 | 19
| | 61 | 13 | 50 | 18 | 16 | 48 | 51 | 3 | | 60 | 44 | 7 | 23 | 41 | 57 | 6 | 22
| | 28 | 12 | 55 | 39 | 25 | 9 | 38 | 54
| |
Cuadrados pares individuales: El cuadrado de Medjig de orden 1 no existe. Como tal, el cuadrado medjig ordenado impar más pequeño es de orden 3, con constante mágica 9. Solo hay 7 formas de dividir el número entero 9, nuestra constante mágica, en tres partes. Si estas tres partes corresponden a tres de las piezas medjig en una fila, columna o diagonal, entonces las particiones relevantes para nosotros son:
- 9 = 1 + 3 + 5 = 1 + 4 + 4 = 2 + 3 + 4 = 2 + 2 + 5 = 3 + 3 + 3.
Se puede construir un cuadrado medjig de 3 × 3 con un poco de prueba y error, como en el cuadrado más a la izquierda a continuación. Otro enfoque es agregar una fila y una columna a un cuadrado medjig de 2 × 2. En el cuadrado del medio a continuación, se agregaron una columna izquierda y una fila inferior, creando un borde medjig en forma de L, a un cuadrado medjig de 2 × 2 dado anteriormente. El cuadrado más a la derecha a continuación es esencialmente el mismo que el cuadrado del medio, excepto que la fila y la columna se agregaron en el medio para formar una cruz, mientras que las piezas del cuadrado medjig de 2 × 2 se colocan en las esquinas.
Medjig 3 × 3
| 2 | 3 | 0 | 2 | 0 | 2
| | 1 | 0 | 3 | 1 | 3 | 1
| | 3 | 1 | 1 | 2 | 2 | 0
| | 0 | 2 | 0 | 3 | 3 | 1
| | 3 | 2 | 2 | 0 | 0 | 2
| | 0 | 1 | 3 | 1 | 1 | 3
| | Medjig 3 × 3
| 0 | 3 | 0 | 1 | 3 | 2
| | 2 | 1 | 2 | 3 | 1 | 0
| | 3 | 0 | 3 | 2 | 0 | 1
| | 2 | 1 | 1 | 0 | 2 | 3
| | 0 | 1 | 3 | 1 | 3 | 1
| | 2 | 3 | 0 | 2 | 0 | 2
| | Medjig 3 × 3
| 0 | 1 | 0 | 3 | 3 | 2
| | 2 | 3 | 2 | 1 | 1 | 0
| | 3 | 1 | 0 | 1 | 3 | 1
| | 0 | 2 | 2 | 3 | 0 | 2
| | 3 | 2 | 3 | 0 | 0 | 1
| | 1 | 0 | 2 | 1 | 2 | 3
| |
Una vez que se ha construido un cuadrado medjig de 3×3, se puede convertir en un cuadrado mágico de 6×6. Por ejemplo, usando el cuadrado medjig de 3 × 3 más a la izquierda dado anteriormente:
| Medjig 3 × 3
| 2 | 3 | 0 | 2 | 0 | 2
| | 1 | 0 | 3 | 1 | 3 | 1
| | 3 | 1 | 1 | 2 | 2 | 0
| | 0 | 2 | 0 | 3 | 3 | 1
| | 3 | 2 | 2 | 0 | 0 | 2
| | 0 | 1 | 3 | 1 | 1 | 3
| | Orden 6
| 26 | 35 | 1 | 19 | 6 | 24
| | 17 | 8 | 28 | 10 | 33 | 15
| | 30 | 12 | 14 | 23 | 25 | 7 | | 3 | 21 | 5 | 32 | 34 | 16
| | 31 | 22 | 27 | 9 | 2 | 20
| | 4 | 13 | 36 | 18 | 11 | 29
| |
Hay 1.740.800 de estos cuadrados medjig de 3×3. Un enfoque fácil para construir un cuadrado medjig impar de orden superior es envolver un cuadrado medjig impar más pequeño con un borde medjig, al igual que con los cuadrados medjig ordenados pares. Otro enfoque consiste en agregar una fila y una columna a un cuadrado medjig incluso ordenado. También se pueden utilizar enfoques como el método LUX. En el siguiente ejemplo, se crea un cuadrado medjig de 5×5 envolviendo un borde medjig alrededor de un cuadrado medjig de 3×3 dado anteriormente:
Orden 5
| 17 | 24 | 1 | 8 | 15
| | 23 | 5 | 7 | 14 | 16
| | 4 | 6 | 13 | 20 | 22
| | 10 | 12 | 19 | 21 | 3
| | 11 | 18 | 25 | 2 | 9
| | Medjig 5 × 5
| 0 | 1 | 3 | 1 | 0 | 1 | 3 | 1 | 3 | 2
| | 2 | 3 | 0 | 2 | 2 | 3 | 0 | 2 | 1 | 0
| | 3 | 0 | 2 | 3 | 0 | 2 | 0 | 2 | 1 | 2
| | 1 | 2 | 1 | 0 | 3 | 1 | 3 | 1 | 3 | 0
| | 0 | 2 | 3 | 1 | 1 | 2 | 2 | 0 | 1 | 3
| | 1 | 3 | 0 | 2 | 0 | 3 | 3 | 1 | 0 | 2
| | 3 | 0 | 3 | 2 | 2 | 0 | 0 | 2 | 1 | 2
| | 1 | 2 | 0 | 1 | 3 | 1 | 1 | 3 | 3 | 0
| | 3 | 2 | 1 | 3 | 1 | 0 | 1 | 3 | 0 | 1
| | 1 | 0 | 2 | 0 | 3 | 2 | 2 | 0 | 2 | 3
| | Orden 10
| 17 | 42 | 99 | 49 | 1 | 26 | 83 | 33 | 90 | 65
| | 67 | 92 | 24 | 74 | 51 | 76 | 8 | 58 | 40 | 15 | | 98 | 23 | 55 | 80 | 7 | 57 | 14 | 64 | 41 | 66
| | 48 | 73 | 30 | 5 | 82 | 32 | 89 | 39 | 91 | 16 | | 4 | 54 | 81 | 31 | 38 | 63 | 70 | 20 | 47 | 97
| | 29 | 79 | 6 | 56 | 13 | 88 | 95 | 45 | 22 | 72
| | 85 | 10 | 87 | 62 | 69 | 19 | 21 | 71 | 28 | 53
| | 35 | 60 | 12 | 37 | 94 | 44 | 46 | 96 | 78 | 3 | | 86 | 61 | 43 | 93 | 100 | 25 | 27 | 77 | 9 | 34
| | 36 | 11 | 68 | 18 | 95 | 75 | 52 | 2 | 59 | 84
| |
Resolver cuadrados mágicos parcialmente completados
Resolver cuadrados mágicos parcialmente completados es un pasatiempo matemático popular. Las técnicas necesarias son similares a las que se utilizan en los rompecabezas de Sudoku o KenKen, e implican deducir los valores de los cuadrados vacíos utilizando la lógica y la teoría de grupos de permutación (las cuadrículas de Sudoku no son cuadrados mágicos, sino que se basan en una idea relacionada llamada cuadrados greco-latinos).
Variaciones del cuadrado mágico
Restricciones adicionales

Plaza mágica de Ramanujan
Se pueden imponer ciertas restricciones adicionales a los cuadrados mágicos.
Si elevando cada número a la nésima potencia se obtiene otro cuadrado mágico, el resultado es una bimagia (n = 2), una trimagia (n = 3) o, en general, una multimagia cuadrado.
Un cuadrado mágico en el que el número de letras en el nombre de cada número en el cuadrado genera otro cuadrado mágico se denomina cuadrado alfamágico.
Hay cuadrados mágicos que consisten enteramente en números primos. Rudolf Ondrejka (1928–2001) descubrió el siguiente cuadrado mágico de números primos de 3 × 3, en este caso nueve números primos Chen:
El teorema de Green-Tao implica que existen cuadrados mágicos arbitrariamente grandes formados por números primos.
El siguiente "cuadrado mágico reversible" tiene una constante mágica de 264 tanto al revés como al revés:
| 96 | 11 | 89 | 68
|
| 88 | 69 | 91 | 16
|
| 61 | 86 | 18 | 99
|
| 19 | 98 | 66 | 81
|
Cuando la restricción adicional es mostrar alguna fecha, especialmente una fecha de nacimiento, estos cuadrados mágicos se denominan cuadrados mágicos de cumpleaños. Srinivasa Ramanujan creó un ejemplo temprano de dicho cuadrado mágico de cumpleaños. Creó un cuadrado de 4×4 en el que ingresó su fecha de nacimiento en formato DD-MM-CC-YY en la fila superior y la magia sucedió con sumas y restas de números en cuadrados. No solo las filas, las columnas y las diagonales suman el mismo número, sino que las cuatro esquinas, los cuatro cuadrados del medio (17, 9, 24, 89), la primera y la última fila dos números del medio (12, 18, 86, 23), y la primera y última columna dos números del medio (88, 10, 25, 16) suman 139.
Cuadrados mágicos multiplicativos
En lugar de sumar los números en cada fila, columna y diagonal, se puede aplicar alguna otra operación. Por ejemplo, un cuadrado mágico multiplicativo tiene un producto constante de números. Un cuadrado mágico multiplicativo se puede derivar de un cuadrado mágico aditivo elevando 2 (o cualquier otro número entero) a la potencia de cada elemento, porque el logaritmo del producto de 2 números es la suma del logaritmo de cada uno. Alternativamente, si 3 números cualesquiera en una línea son 2a, 2b y 2c, su producto es 2a+b+c, que es constante si a+b+c es constante, como lo serían si a, b y c se tomaron del cuadrado mágico ordinario (aditivo). Por ejemplo, el cuadrado mágico original de Lo-Shu se convierte en:
M = 32768
| 16 | 512 | 4
|
| 8 | 32 | 128
|
| 256 | 2 | 64
|
Otros ejemplos de cuadrados mágicos multiplicativos incluyen:
| M = 6720
| 1 | 6 | 20 | 56
| | 40 | 28 | 2 | 3
| | 14 | 5 | 24 | 4
| | 12 | 8 | 7 | 10
| | M = 6.227.020.800
| 27 | 50 | 66 | 84 | 13 | 2 | 32
| | 24 | 52 | 3 | 40 | 54 | 70 | 11
| | 56 | 9 | 20 | 44 | 36 | 65 | 6
| | 55 | 72 | 91 | 1 | 16 | 36 | 30
| | 4 | 24 | 45 | 60 | 77 | 12 | 26
| | 10 | 22 | 48 | 39 | 5 | 48 | 63
| | 78 | 7 | 8 | 18 | 40 | 33 | 60
| |
Cuadrados mágicos multiplicativos de números complejos
Todavía utilizando el método no iterativo de Ali Skalli, es posible producir un infinito de cuadrados de magia multiplicativa de números complejos pertenecientes a C{displaystyle mathbb {C} Listo. En el ejemplo a continuación, las partes reales e imaginarias son números enteros, pero también pueden pertenecer a todo el conjunto de números reales R{displaystyle mathbb {R}
Listo. En el ejemplo a continuación, las partes reales e imaginarias son números enteros, pero también pueden pertenecer a todo el conjunto de números reales R{displaystyle mathbb {R} .
El producto es: −352,507,340,640 − 400,599,719,520 i.
.
El producto es: −352,507,340,640 − 400,599,719,520 i.
Skalli multiplicativo 7×7 de números complejos
| 21 | +14i | ,70 - 70 | +30i | ,93 - 93 | −9i | −105 | −217i | 16 | +50i | 4 | −14i | 14 | −8i |
| 63 | −35i | 28 | +114i | | −14i | 2 | +6i | 3 | −11 -i | 211 | +357i | −123 | −87i |
| 31 | −15i | 13 | −13i | −103 | +69i | −26-1 | −213i | 49 | ,49 - 49i | 46 - | +2i | −6 | +2i |
| 102 | ,84 - 84i | −28 | −14i | 43 | +247i | −10 | −2i | 5 | +9i | 31 | −27i | −77− | +91i |
| −22 | −6i | 7 | +7i | 8 | +14i | 50 | +20i | ,5 a 25 | −492i | −28 | −42i | ,73 - 73 | +17i |
| 54 | +68i | 138 | −165i | −56− | 98−i | −63− | +35i | 4 | −8i | 2 | −4i | 70 | .53 -i |
| 24 | +22i | 46 - | −16i | 6 | −4i | 17 | +20i | 110 | +160i | 84 | −189i | 42 | −14i |
Cuadrados mágicos y semimágicos aditivos-multiplicativos
Los cuadrados mágicos aditivos multiplicativos y los cuadrados semimágicos satisfacen las propiedades de los cuadrados mágicos ordinarios y multiplicativos y los cuadrados semimágicos, respectivamente.
First known
aditivo-multiplicativo cuadrado mágico
8×8 encontrado por W. W. Horner en 1955
Sum = 840
Producto = 2058068231856000| 162 | 207 | 51 | 26 | 133 | 120 | 116 | 25
| | 105 | 152 | 100 | 29 | 138 | 243 | 39 | 34
| | 92 | 27 | 91 | 136 | 45 | 38 | 150 | 261
| | 57 | 30 | 174 | 225 | 108 | 23 | 119 | 104
| | 58 | 75 | 171 | 90 | 17 | 52 | 216 | 161
| | 13 | 68 | 184 | 189 | 50 | 87 | 135 | 114
| | 200 | 203 | 15 | 76 | 117 | 102 | 46 | 81
| | 153 | 78 | 54 | 69 | 232 | 175 | 19 | 60
| | cuadrado semimagnético más pequeño conocido aditivo-multiplicativo
4×4 encontrado por L. Morgenstern en 2007
Sum = 247
Producto = 3369600
| 156 | 18 | 48 | 25
| | 30 | 144 | 60 | 13
| | 16 | 20 | 130 | 81
| | 45 | 65 | 9 | 128
| |
Se desconoce si existen cuadrados mágicos multiplicativos aditivos menores que 8 × 8, pero se ha demostrado que no existen cuadrados mágicos multiplicativos aditivos de 3 × 3 o 4 × 4 ni cuadrados semimágicos multiplicativos aditivos de 3 × 3..
Cuadrados mágicos geométricos

Un cuadrado mágico geométrico.
Se pueden construir cuadrados mágicos que contienen formas geométricas en lugar de números. Tales cuadrados, conocidos como cuadrados mágicos geométricos, fueron inventados y nombrados por Lee Sallows en 2001.
En el ejemplo que se muestra, las formas que aparecen son bidimensionales. Fue Sallows' descubrimiento de que todos los cuadrados mágicos son geométricos, los números que aparecen en los cuadrados mágicos numéricos pueden interpretarse como una notación abreviada que indica las longitudes de los segmentos de línea recta que son las 'formas' que ocurre en la plaza. Es decir, los cuadrados mágicos numéricos son ese caso especial de un cuadrado mágico geométrico que utiliza formas unidimensionales.
Cuadrados mágicos de área

El primer cuadrado mágico de zona lineal
En 2017, siguiendo las ideas iniciales de William Walkington e Inder Taneja, Walter Trump construyó el primer cuadrado mágico de área lineal (L-AMS).
Otras formas mágicas
Se pueden considerar otras formas bidimensionales además de los cuadrados. El caso general es considerar que un diseño con N partes es mágico si las N partes están etiquetadas con los números del 1 al N y un número de subdiseños idénticos dan la misma suma. Los ejemplos incluyen círculos mágicos, rectángulos mágicos, triángulos mágicos, estrellas mágicas, hexágonos mágicos, diamantes mágicos. Subir en dimensión da como resultado esferas mágicas, cilindros mágicos, cubos mágicos, paralelepípedos mágicos, sólidos mágicos y otros hipercubos mágicos.
Las formas mágicas posibles están restringidas por el número de subconjuntos de igual tamaño y suma igual del conjunto de etiquetas elegido. Por ejemplo, si se propone formar una forma mágica etiquetando las partes con {1, 2, 3, 4}, los subdiseños deberán etiquetarse con {1,4} y {2,3}.
Problemas relacionados

Una plaza semimágica (sus diagonales no suman su constante mágica, 260) también formando un recorrido de caballero – no existen tours totalmente mágicos.
Problema de N-Queens
En 1992, Demirörs, Rafraf y Tanik publicaron un método para convertir algunos cuadrados mágicos en soluciones de n-reinas y viceversa.
Cuadrados mágicos en ocultismo
Los cuadrados mágicos de orden 3 a 9, asignados a los siete planetas y descritos como medios para atraer la influencia de los planetas y sus ángeles (o demonios) durante las prácticas mágicas, se pueden encontrar en varios manuscritos de toda Europa que comienzan al menos desde el siglo XV. Entre los más conocidos, el Liber de Angelis, un manual mágico escrito alrededor de 1440, está incluido en Cambridge Univ. lib. MS Dd.xi.45. El texto del Liber de Angelis es muy parecido al de De septem quadraturis planetarum seu quadrati magici, otro manual de magia de imágenes planetarias contenido en el Codex 793 de la Biblioteka Jagiellońska (Sra. BJ 793). Las operaciones mágicas consisten en grabar el cuadrado apropiado en una placa hecha con el metal asignado al planeta correspondiente, así como realizar una variedad de rituales. Por ejemplo, el cuadrado de 3×3, que pertenece a Saturno, tiene que ser inscrito en una placa de plomo. En particular, ayudará a las mujeres durante un parto difícil.
Alrededor de 1510, Heinrich Cornelius Agrippa escribió De Occulta Philosophia, basándose en las obras herméticas y mágicas de Marsilio Ficino y Pico della Mirandola. En su edición de 1531, expuso las virtudes mágicas de los siete cuadrados mágicos de los órdenes 3 a 9, cada uno asociado con uno de los planetas astrológicos, de la misma manera que lo hacían los textos más antiguos. Este libro fue muy influyente en toda Europa hasta la contrarreforma, y los cuadrados mágicos de Agrippa, a veces llamados kameas, continúan usándose dentro de la magia ceremonial moderna de la misma manera que él los prescribió por primera vez.

La derivación del sigil de Hagiel, la inteligencia planetaria de Venus, dibujada en la plaza mágica de Venus. Cada uno La letra hebrea proporciona un valor numérico, dando los vértices del sigil.
El uso más común de estos kameas es proporcionar un patrón sobre el cual construir los sigilos de espíritus, ángeles o demonios; las letras del nombre de la entidad se convierten en números y se trazan líneas a través del patrón que estos números sucesivos hacen en el kamea.
En un contexto mágico, el término cuadrado mágico también se aplica a una variedad de cuadrados de palabras o números que se encuentran en grimorios mágicos, incluidos algunos que no siguen ningún patrón obvio, e incluso aquellos con diferentes números de filas y columnas. Por lo general, están destinados a ser utilizados como talismanes. Por ejemplo, los siguientes cuadrados son: El cuadrado Sator, uno de los cuadrados mágicos más famosos que se encuentran en varios grimorios, incluida la Clave de Salomón; un cuadrado "para vencer la envidia", de El Libro del Poder; y dos cuadrados de El Libro de la Magia Sagrada de Abramelin el Mago, el primero para hacer aparecer la ilusión de un soberbio palacio, y el segundo para ser usado en la cabeza de un niño durante una velada angelical. invocación:
| S | A | T | O | R
| | A | R | E | P | O
| | T | E | N | E | T
| | O | P | E | R | A
| | R | O | T | A | S
|
| | 6 | 66 | 848 | 938
| | 8 | 11 | 544 | 839
| | 1 | 11 | 383 | 839
| | 2 | 73 | 774 | 447
|
| | |
Cuadrados mágicos en la cultura popular

Estampón de Macao con cuadrado de magia geométrica
- En el Faust de Goethe, el hechizo de la bruja solía hacer un elixir juvenil para Faust, el Hexen-Einmal-Eins[de], ha sido interpretado como una construcción de una plaza mágica.
- El compositor inglés Peter Maxwell Davies ha utilizado cuadrados mágicos para estructurar muchas de sus composiciones. Por ejemplo, su 1975 Ave Maris Stella utiliza la plaza mágica 9×9 de la Luna mientras su 1977 Un espejo de la luz blanqueadora utiliza el cuadrado mágico 8×8 de Mercurio para crear todo el conjunto de notas y duración para la pieza. Sus otras obras que emplean cuadrados mágicos incluyen The Lighthouse (1979), Resurrection (1987), Strathclyde Concerto No. 3 para Horn y Trumpet (1989), así como muchas de sus sinfonías. Según la cuenta de Davies:
Un cuadrado mágico en una composición musical no es un bloque de números – es un principio generador, ser aprendido y conocido íntimamente, percibido internamente como una proyección multidimensional en esa vasta (chaotic!) área del oído interno – el espacio/tiempo crisol – donde se concibe la música.... Proyectado en la página, una plaza mágica es una conglomeración muerta y negra de dígitos; sintoniza, y se oye un poderoso dinamo orbitante de imágenes musicales, brillando con numen y lumen.
- Los cuadrados mágicos, incluyendo los de Benjamin Franklin, aparecen como pistas del misterio en las novelas de Katherine Neville Los Ocho y El Fuego.
- Los cuadrados mágicos juegan un papel en la novela de Steve Martin 2003 El Placer de Mi Compañía.
- El cuadrado mágico de Durero y su Melencolia I ambos también jugaron grandes roles en la novela de Dan Brown 2009, El símbolo perdido.
- En el drama de la televisión coreana 2011 Árbol profundo, King Sejong se muestra tratando de construir un cuadrado mágico de 33×33 utilizando cajas de almuerzo. Él finalmente descubre el "método pirámide" y completa la plaza mágica con la ayuda de un ejército de asistentes a la corte. Esto lo inspira a crear una forma más justa de gobierno gobernado por la razón y las palabras en lugar de poder militar.
- El 9 de octubre de 2014 la oficina postal de Macao en la República Popular China emitió una serie de sellos basados en cuadrados mágicos. La figura a continuación muestra los sellos con los nueve cuadrados mágicos elegidos para estar en esta colección.
- El artefacto metálico en el centro de Los X-Files episodio "Biogenesis" es denunciado por Chuck Burks para ser una plaza mágica.
- El matemático Matt Parker intentó crear un cuadrado mágico de 3×3 utilizando números cuadrados en un video de YouTube en el canal de Numphile. Su intento fallido es conocido como la Plaza Parker.
- La primera temporada Stargate Atlantis episodio "Brotherhood" implica completar una plaza mágica como parte de un rompecabezas que protege un poderoso artefacto antiguo.
- Magia Los cuadrados también aparecen en la película española Vivir dos veces.

5" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/8bd2bf6a3536376e04ca3924122de04b11344796" style="vertical-align: -0.338ex; width:5.656ex; height:2.176ex;"/>?