Cristian huygens

Christiaan HuygensSeñor de Zeelhem, FRS (HY-gnz, HOY-gnz, Dutch:[en inglés] ()escucha); también deletreado Huyghens; Latín: Hugenius; 14 abril 1629 – 8 julio 1695) fue un matemático holandés, físico, ingeniero, astrónomo e inventor, que se considera una de las figuras más importantes de la Revolución Científica. En física, Huygens hizo contribuciones originales a la óptica y la mecánica, mientras que como astrónomo es principalmente conocido por sus estudios de los anillos de Saturno y el descubrimiento de su Titan Luna. Como ingeniero e inventor, mejoró el diseño de telescopios e inventó el reloj péndulo, un avance en el mantenimiento del tiempo y el cronograma más preciso durante casi 300 años. Un matemático y físico excepcionalmente talentoso, Huygens fue el primero en idealizar un problema físico por un conjunto de parámetros matemáticos, y el primero en elaborar una explicación mecanicista de un fenómeno físico inservible. Por estas razones, ha sido llamado el primer físico teórico y uno de los fundadores de la física matemática moderna.

Huygens identificó por primera vez las leyes correctas de la colisión elástica en su obra De Motu Corporum ex Percussione, completada en 1656 pero publicada póstumamente en 1703. En 1659, Huygens derivó geométricamente la fórmula de la mecánica clásica para la fuerza centrífuga en su obra De vi Centrifuga, una década antes de Newton. En óptica, es más conocido por su teoría ondulatoria de la luz, que describió en su Traité de la Lumière (1690). Su teoría de la luz fue inicialmente rechazada a favor de la teoría corpuscular de la luz de Newton, hasta que Augustin-Jean Fresnel adoptó el principio de Huygens para dar una explicación completa de la propagación rectilínea y los efectos de difracción de la luz en 1821. Hoy este principio se conoce como el principio de Huygens-Fresnel.

Huygens inventó el reloj de péndulo en 1657, que patentó el mismo año. Su investigación relojera dio como resultado un extenso análisis del péndulo en Horologium Oscillatorium (1673), considerado como uno de los trabajos más importantes del siglo XVII sobre mecánica. Si bien contiene descripciones de diseños de relojes, la mayor parte del libro es un análisis del movimiento pendular y una teoría de las curvas. En 1655, Huygens comenzó a moler lentes con su hermano Constantijn para construir telescopios refractores. Descubrió la primera de las lunas de Saturno, Titán, y fue el primero en explicar la extraña apariencia de Saturno como debida a "un anillo delgado y plano, que no se toca en ninguna parte e inclinado hacia la eclíptica". #34; En 1662, Huygens desarrolló lo que ahora se llama el ocular Huygenian, un telescopio con dos lentes para disminuir la cantidad de dispersión.

Como matemático, Huygens desarrolló la teoría de las evolutas y escribió sobre los juegos de azar y el problema de los puntos en Van Rekeningh in Spelen van Gluck, que Frans van Schooten tradujo y publicó como De Ratiociniis en Ludo Aleae (1657). El uso de valores esperados por parte de Huygens y otros más tarde inspiraría el trabajo de Jacob Bernoulli sobre la teoría de la probabilidad.

Biografía

Retrato de Constantijn (centro) y sus cinco hijos (Christiaan, superior derecha). Mauritshuis, La Haya.

Christiaan Huygens nació el 14 de abril de 1629 en La Haya, en el seno de una rica e influyente familia holandesa, segundo hijo de Constantijn Huygens. Christiaan recibió su nombre de su abuelo paterno. Su madre, Suzanna van Baerle, murió poco después de dar a luz a la hermana de Huygens. La pareja tuvo cinco hijos: Constantijn (1628), Christiaan (1629), Lodewijk (1631), Philips (1632) y Suzanna (1637).

Constantijn Huygens fue diplomático y asesor de la Casa de Orange, además de poeta y músico. Mantuvo una amplia correspondencia con intelectuales de toda Europa; sus amigos incluían a Galileo Galilei, Marin Mersenne y René Descartes. Christiaan fue educado en casa hasta los dieciséis años, y desde muy joven le gustaba jugar con miniaturas de molinos y otras máquinas. De su padre recibió una educación liberal, estudiando idiomas, música, historia, geografía, matemáticas, lógica y retórica, además de baile, esgrima y equitación.

En 1644, Huygens tuvo como tutor matemático a Jan Jansz Stampioen, quien le asignó al joven de 15 años una exigente lista de lecturas sobre ciencia contemporánea. Más tarde, Descartes quedó impresionado por sus habilidades en geometría, al igual que Mersenne, quien lo bautizó como "el nuevo Arquímedes".

Años de estudiante

A los dieciséis años, Constantijn envió a Huygens a estudiar leyes y matemáticas en la Universidad de Leiden, donde estudió desde mayo de 1645 hasta marzo de 1647. Frans van Schooten fue académico en Leiden desde 1646 y se convirtió en tutor privado de Huygens y su hermano mayor, Constantijn Jr., reemplazando a Stampioen por consejo de Descartes. Van Schooten actualizó la educación matemática de Huygens, introduciéndolo al trabajo de Viète, Descartes y Fermat.

Después de dos años, a partir de marzo de 1647, Huygens continuó sus estudios en el recién fundado Orange College, en Breda, donde su padre era curador. Constantijn Huygens estuvo muy involucrado en el nuevo Colegio, que duró solo hasta 1669; el rector era André Rivet. Christiaan Huygens vivió en la casa del jurista Johann Henryk Dauber mientras asistía a la universidad y tenía clases de matemáticas con el profesor de inglés John Pell. Su tiempo en Breda terminó cuando su hermano Lodewijk, que estaba inscrito en la escuela, se batió en duelo con otro estudiante. Huygens dejó Breda después de completar sus estudios en agosto de 1649 y tuvo una temporada como diplomático en una misión con Enrique, duque de Nassau. Lo llevó a Bentheim, luego a Flensburg. Partió hacia Dinamarca, visitó Copenhague y Helsingør, y esperaba cruzar el Oresund para visitar a Descartes en Estocolmo. No iba a ser.

Aunque su padre Constantijn deseaba que su hijo Christiaan fuera diplomático, las circunstancias impidieron que lo fuera. El Primer Período sin Estatúderes que comenzó en 1650 significó que la Casa de Orange ya no estaba en el poder, eliminando la influencia de Constantino. Además, se dio cuenta de que su hijo no tenía ningún interés en esa carrera.

Correspondencia temprana

Imagen de una cadena colgante (catenario) en un manuscrito de Huygens.

Huygens generalmente escribía en francés o latín. En 1646, cuando aún era estudiante universitario en Leiden, comenzó una correspondencia con el amigo de su padre, Marin Mersenne, quien murió poco después en 1648. Mersenne le escribió a Constantijn sobre el talento de su hijo para las matemáticas y lo comparó halagadoramente con Arquímedes el 3 de enero de 1647.

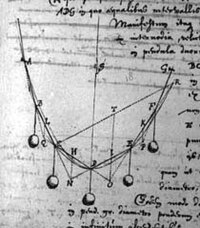
Las cartas muestran el temprano interés de Huygens por las matemáticas. En octubre de 1646 se produce el puente colgante y la demostración de que una cadena colgante no es una parábola, como pensaba Galileo. Huygens más tarde etiquetaría esa curva como la catenaria (catenaria) en 1690 mientras mantenía correspondencia con Gottfried Leibniz.

En los siguientes dos años (1647-48), las cartas de Huygens a Mersenne cubrieron varios temas, incluida una prueba matemática de la ley de caída libre, la afirmación de Grégoire de Saint-Vincent de la cuadratura del círculo, que Huygens demostró estar equivocado, la rectificación de la elipse, los proyectiles y la cuerda vibrante. Algunas de las preocupaciones de Mersenne en ese momento, como la cicloide (envió el tratado de Huygens Torricelli sobre la curva), el centro de oscilación y la constante gravitacional, eran asuntos que Huygens solo tomó en serio hacia el final. del siglo XVII. Mersenne también había escrito sobre teoría musical. Huygens prefería el temperamento de tono medio; innovó en 31 temperamento igual (que no era en sí mismo una idea nueva pero conocida por Francisco de Salinas), utilizando logaritmos para investigarlo más a fondo y mostrar su estrecha relación con el sistema de medios tonos.

En 1654, Huygens regresó a la casa de su padre en La Haya y pudo dedicarse por completo a la investigación. La familia tenía otra casa, no muy lejos en Hofwijck, y él pasaba un tiempo allí durante el verano. A pesar de ser muy activo, su vida académica no le permitió escapar de los episodios de depresión.

Posteriormente, Huygens desarrolló una amplia gama de corresponsales, aunque retomar los hilos después de 1648 se vio obstaculizado por la Fronda de cinco años en Francia. Al visitar París en 1655, Huygens llamó a Ismael Boulliau para que se presentara, quien lo llevó a ver a Claude Mylon. El grupo parisino de sabios que se había reunido en torno a Mersenne se mantuvo unido hasta la década de 1650, y Mylon, que había asumido el papel de secretario, se tomó algunas molestias para mantener a Huygens en contacto. A través de Pierre de Carcavi, Huygens mantuvo correspondencia en 1656 con Pierre de Fermat, a quien admiraba mucho, aunque de este lado de la idolatría. La experiencia fue agridulce y un tanto desconcertante, ya que quedó claro que Fermat se había retirado de la corriente principal de la investigación, y sus afirmaciones de prioridad probablemente no podrían cumplirse en algunos casos. Además, para entonces Huygens buscaba aplicar las matemáticas a la física, mientras que las preocupaciones de Fermat se dirigían a temas más puros.

Debut científico

Christiaan Huygens, relieve de Jean-Jacques Clérion (c. 1670).

Al igual que algunos de sus contemporáneos, Huygens a menudo tardó en enviar sus resultados y descubrimientos a la imprenta, prefiriendo difundir su trabajo a través de cartas. En sus primeros días, su mentor, Frans van Schooten, proporcionó comentarios técnicos y fue cauteloso por el bien de su reputación.

Entre 1651 y 1657, Huygens publicó una serie de obras que mostraban su talento para las matemáticas y su dominio de la geometría clásica y analítica, aumentando su alcance y reputación entre los matemáticos. Casi al mismo tiempo, Huygens comenzó a cuestionar las leyes de colisión de Descartes, que en gran medida eran incorrectas, deduciendo las leyes correctas algebraicamente y luego por medio de la geometría. Demostró que, para cualquier sistema de cuerpos, el centro de gravedad del sistema permanece igual en velocidad y dirección, lo que Huygens llamó la conservación de la "cantidad de movimiento". Mientras que otros estudiaban el impacto en la misma época, la teoría de las colisiones de Huygens era más general. Estos resultados se conocieron a través de correspondencia y en un breve artículo en Journal des Sçavans pero permanecerían en gran parte inéditos hasta después de su muerte, con la publicación de De Motu Corporum ex Percussione (Sobre el movimiento de cuerpos en colisión).

Además de su trabajo sobre mecánica, realizó importantes descubrimientos científicos, como la identificación de la luna de Saturno, Titán, en 1655, y la invención del reloj de péndulo en 1657, que le dieron fama en toda Europa.. El 3 de mayo de 1661, Huygens observó el tránsito del planeta Mercurio sobre el Sol, utilizando el telescopio del fabricante de instrumentos Richard Reeve en Londres, junto con el astrónomo Thomas Streete y Reeve. Streete luego debatió el registro publicado del tránsito de Hevelius, una controversia mediada por Henry Oldenburg. Huygens pasó a Hevelius un manuscrito de Jeremiah Horrocks sobre el tránsito de Venus, 1639, que se imprimió por primera vez en 1662.

Sir Robert Moray envió a Huygens la tabla de vida de John Graunt en 1662 y, con el tiempo, Huygens y su hermano Lodewijk se interesaron por la esperanza de vida. Huygens finalmente creó el primer gráfico de una función de distribución continua bajo el supuesto de una tasa de mortalidad uniforme y la utilizó para resolver problemas en anualidades conjuntas. En el mismo año, Huygens, que tocaba el clavicémbalo, se interesó por las teorías musicales de Simon Stevin; sin embargo, mostró muy poca preocupación por publicar sus teorías sobre la consonancia, algunas de las cuales se perdieron durante siglos. Por sus contribuciones a la ciencia, la Royal Society de Londres eligió a Huygens como miembro en 1665, convirtiéndolo en su primer miembro extranjero cuando tenía solo 36 años.

Francia

Huygens, derecho de centro, desde L'établissement de l'Académie des Sciences et fondation de l'observatoire, 1666 por Henri Testelin (c. 1675).

La Academia Montmor fue la forma que tomó el antiguo círculo de Mersenne después de mediados de la década de 1650. Huygens participó en sus debates y apoyó a su "disidente" facción que favorecía la demostración experimental para reducir la discusión infructuosa y se oponía a las actitudes de aficionados. Durante 1663 realizó la que fue su tercera visita a París; la Academia Montmor cerró y Huygens aprovechó la oportunidad para abogar por un programa científico más baconiano. Tres años más tarde, en 1666, se mudó a París por invitación de ocupar un puesto en la nueva Académie des sciences francesa del rey Luis XIV.

Mientras estuvo en París, Huygens tuvo un importante mecenas y corresponsal en Jean-Baptiste Colbert, primer ministro de Luis XIV. Sin embargo, su relación con la Academia Francesa no siempre fue fácil, y en 1670 Huygens, gravemente enfermo, eligió a Francis Vernon para realizar una donación de sus papeles a la Royal Society de Londres, en caso de que falleciera. Las secuelas de la guerra franco-holandesa (1672-1678), y particularmente el papel de Inglaterra en ella, pueden haber dañado su relación con la Royal Society. Robert Hooke, como representante de la Royal Society, careció de la delicadeza para manejar la situación en 1673.

El físico e inventor Denis Papin fue ayudante de Huygens desde 1671. Uno de sus proyectos, que no fructificó directamente, fue el motor de pólvora. Papin se mudó a Inglaterra en 1678 para continuar trabajando en esta área. También en París, Huygens realizó más observaciones astronómicas utilizando el observatorio recién terminado en 1672. Presentó a Nicolaas Hartsoeker a científicos franceses como Nicolas Malebranche y Giovanni Cassini en 1678.

Huygens conoció a Leibniz cuando era un joven diplomático, visitando París en 1672 en una vana misión para reunirse con el Ministro de Asuntos Exteriores francés Arnauld de Pomponne. En ese momento, Leibniz estaba trabajando en una máquina calculadora y se mudó a Londres a principios de 1673 con diplomáticos de Maguncia. Desde marzo de 1673, Leibniz fue instruido en matemáticas por Huygens, quien le enseñó geometría analítica. Siguió una extensa correspondencia, en la que Huygens mostró al principio renuencia a aceptar las ventajas del cálculo infinitesimal de Leibniz.

Últimos años

Huygens regresó a La Haya en 1681 después de sufrir otro episodio de una grave enfermedad depresiva. En 1684, publicó Astroscopia Compendiaria sobre su nuevo telescopio aéreo sin cámara. Intentó regresar a Francia en 1685, pero la revocación del Edicto de Nantes lo impidió. Su padre murió en 1687 y heredó Hofwijck, que convirtió en su hogar al año siguiente.

En su tercera visita a Inglaterra, Huygens conoció personalmente a Isaac Newton el 12 de junio de 1689. Hablaron sobre el espato de Islandia y, posteriormente, mantuvieron correspondencia sobre el movimiento resistido.

Huygens volvió a los temas matemáticos en sus últimos años y observó el fenómeno acústico ahora conocido como flanger en 1693. Dos años más tarde, el 8 de julio de 1695, Huygens murió en La Haya y fue enterrado en una tumba sin nombre en Grote Kerk allí., como lo fue su padre antes que él.

Huygens nunca se casó.

Matemáticas

Huygens primero se hizo conocido internacionalmente por su trabajo en matemáticas, publicando una serie de resultados importantes que llamaron la atención de muchos geómetras europeos. El método preferido de Huygens en sus obras publicadas fue el de Arquímedes, aunque utilizó la geometría analítica de Descartes y las técnicas infinitesimales de Fermat de manera más extensa en sus cuadernos privados.

Obras publicadas

Teoremas de Cuadratura

La primera publicación de Huygens fue en el campo de la cuadratura.

La primera publicación de Huygens fue Theoremata de Quadratura Hyperboles, Ellipsis et Circuli (Teoremas sobre la cuadratura de la hipérbola, la elipse y el círculo), publicado por los Elzevier en Leiden en 1651. La primera parte del trabajo contenía teoremas para calcular las áreas de hipérbolas, elipses y círculos que eran paralelos al trabajo de Arquímedes sobre las secciones cónicas, particularmente su Cuadratura de la parábola. La segunda parte incluía una refutación de las afirmaciones de Grégoire de Saint-Vincent sobre la cuadratura circular, que había discutido con Mersenne anteriormente.

Huygens demostró que el centro de gravedad de un segmento de cualquier hipérbola, elipse o círculo estaba directamente relacionado con el área de ese segmento. Luego pudo mostrar las relaciones entre triángulos inscritos en secciones cónicas y el centro de gravedad de esas secciones. Al generalizar estos teoremas a todas las secciones cónicas, Huygens amplió los métodos clásicos para generar nuevos resultados.

La cuadratura era un tema candente en la década de 1650 y, a través de Mylon, Huygens intervino en la discusión de las matemáticas de Thomas Hobbes. Persistiendo en tratar de explicar los errores en los que había caído Hobbes, se ganó una reputación internacional.

De Circuli Magnitudine Inventa

La siguiente publicación de Huygens fue De Circuli Magnitudine Inventa (Nuevos hallazgos en la medición del círculo), publicado en 1654. En este trabajo, Huygens fue capaz de reducir la brecha entre los polígonos circunscritos e inscritos que se encuentran en la Medida del círculo de Arquímedes, mostrando que la relación entre la circunferencia y su diámetro o π debe estar en el primer tercio de ese intervalo.

Usando una técnica equivalente a la extrapolación de Richardson, Huygens pudo acortar las desigualdades utilizadas en el método de Arquímedes; en este caso, al usar el centro de gravedad de un segmento de una parábola, pudo aproximar el centro de gravedad de un segmento de un círculo, lo que resultó en una aproximación más rápida y precisa de la cuadratura del círculo. A partir de estos teoremas, Huygens obtuvo dos conjuntos de valores para π: el primero entre 3,1415926 y 3,1415927, y el segundo entre 3,1415926538 y 3,1415926533.

Huygens también demostró que, en el caso de la hipérbola, la misma aproximación con segmentos parabólicos produce un método rápido y sencillo para calcular logaritmos. Anexó una colección de soluciones a problemas clásicos al final de la obra bajo el título Illustrium Quorundam Problematum Constructiones (Construcción de algunos problemas ilustres).

De Ratiociniis en Ludo Aleae

Huygens se interesó en los juegos de azar después de que visitó París en 1655 y se encontró con el trabajo de Fermat, Blaise Pascal y Girard Desargues años antes. Finalmente publicó lo que fue, en ese momento, la presentación más coherente de un enfoque matemático de los juegos de azar en De Ratiociniis in Ludo Aleae (Sobre el razonamiento en los juegos de azar).. Frans van Schooten tradujo el manuscrito holandés original al latín y lo publicó en su Exercitationum Mathematicarum (1657).

El trabajo contiene ideas tempranas de teoría de juegos y trata en particular el problema de los puntos. Huygens tomó de Pascal los conceptos de un "juego justo" y contrato equitativo (es decir, división igual cuando las posibilidades son iguales), y amplió el argumento para establecer una teoría no estándar de los valores esperados. Su éxito al aplicar el álgebra al reino del azar, que hasta entonces parecía inaccesible a los matemáticos, demostró el poder de combinar las pruebas sintéticas euclidianas con el razonamiento simbólico que se encuentra en las obras de Viète y Descartes.

Huygens incluyó cinco problemas desafiantes al final del libro que se convirtieron en la prueba estándar para cualquiera que desee mostrar su habilidad matemática en juegos de azar durante los siguientes sesenta años. Las personas que trabajaron en estos problemas incluyeron a Abraham de Moivre, Jacob Bernoulli, Johannes Hudde, Baruch Spinoza y Leibniz.

Obra inédita

Hofwijck, la casa de verano de Huygens.

Huygens había completado anteriormente un manuscrito a la manera de Sobre los cuerpos flotantes de Arquímedes titulado De Iis quae Liquido Supernatant (Sobre las partes que flotan sobre líquidos ). Fue escrito alrededor de 1650 y estaba compuesto por tres libros. Aunque envió el trabajo completo a Frans van Schooten para recibir comentarios, al final, Huygens decidió no publicarlo y en un momento sugirió que se quemara. Algunos de los resultados encontrados aquí no fueron redescubiertos hasta los siglos XVIII y XIX.

Huygens primero vuelve a derivar los resultados de Arquímedes para la estabilidad de la esfera y el paraboloide mediante una inteligente aplicación del principio de Torricelli (es decir, que los cuerpos en un sistema se mueven solo si su centro de gravedad desciende). Luego demuestra el teorema general de que, para un cuerpo flotante en equilibrio, la distancia entre su centro de gravedad y su parte sumergida es mínima. Huygens usa este teorema para llegar a soluciones originales para la estabilidad de conos, paralelepípedos y cilindros flotantes, en algunos casos a través de un ciclo completo de rotación. Su enfoque era así equivalente al principio del trabajo virtual. Huygens también fue el primero en reconocer que, para sólidos homogéneos, su peso específico y su relación de aspecto son los parámetros esenciales de la estabilidad hidrostática.

Filosofía Natural

Huygens fue el principal filósofo natural europeo entre Descartes y Newton. Sin embargo, a diferencia de muchos de sus contemporáneos, Huygens no tenía gusto por los grandes sistemas teóricos o filosóficos y, en general, evitaba tratar cuestiones metafísicas (si se le presionaba, se adhería a la filosofía cartesiana y mecánica de su tiempo). En cambio, Huygens se destacó en extender el trabajo de sus predecesores, como Galileo, para obtener soluciones a problemas físicos no resueltos que fueran susceptibles de análisis matemático. En particular, buscó explicaciones que se basaran en el contacto entre cuerpos y evitaran la acción a distancia.

Al igual que Robert Boyle y Jacques Rohault, Huygens abogó por una filosofía natural corpuscular-mecánica de orientación experimental durante sus años en París. Este enfoque a veces se denominó "baconiano," sin ser inductivista ni identificarse con los puntos de vista de Francis Bacon de manera simplista.

Después de su primera visita a Inglaterra en 1661 y de asistir a una reunión en Gresham College donde aprendió directamente sobre los experimentos con bombas de aire de Boyle, Huygens dedicó un tiempo a fines de 1661 y principios de 1662 a replicar el trabajo. Resultó ser un proceso largo que trajo a la superficie tanto un problema experimental ("suspensión anómala") como un problema teórico ("horror vacui"), y que finalizó en julio de 1663 cuando Huygens se convirtió en miembro de la Royal Society. Huygens llegó a aceptar la visión de Boyle del vacío frente a la negación cartesiana del mismo, mientras que la replicación de los resultados de los experimentos de Boyle con la bomba de aire se desvaneció desordenadamente.

La influencia de Newton en John Locke estuvo mediada por Huygens, quien le aseguró a Locke que las matemáticas de Newton eran sólidas, lo que llevó a Locke a aceptar una física corpuscular-mecánica.

Leyes de movimiento, impacto y gravitación

Una metáfora de navegación como una manera de pensar en el movimiento relativo, simplificando la teoría de los cuerpos colisionantes, de Huygens Oeuvres Complètes.

El enfoque general de los filósofos mecánicos era postular teorías del tipo que ahora se denomina "acción de contacto". Huygens adoptó este método, pero no sin ver sus dificultades y fracasos. Leibniz, su alumno en París, más tarde abandonó la teoría. Ver el universo de esta manera hizo que la teoría de las colisiones fuera fundamental para la física. La materia en movimiento compuso el universo, y solo las explicaciones en esos términos podrían ser verdaderamente inteligibles. Si bien estuvo influenciado por el enfoque cartesiano, fue menos doctrinario. Estudió colisiones elásticas en la década de 1650, pero retrasó la publicación durante más de una década.

Huygens concluyó bastante pronto que las leyes de Descartes para el choque elástico de dos cuerpos debían ser incorrectas y formuló las leyes correctas, incluida la conservación del producto de la masa por el cuadrado de la velocidad para cuerpos duros, y la conservación de la cantidad de movimiento en una dirección para todos los cuerpos. Un paso importante fue su reconocimiento de la invariancia galileana de los problemas. De hecho, Huygens había elaborado las leyes de colisión entre 1652 y 1656 en un manuscrito titulado De Motu Corporum ex Percussione, aunque sus resultados tardaron muchos años en circular. En 1661, se los pasó en persona a William Brouncker y Christopher Wren en Londres. Lo que Spinoza escribió a Henry Oldenburg sobre ellos en 1666, durante la Segunda Guerra Anglo-Holandesa, fue guardado. La guerra terminó en 1667 y Huygens anunció sus resultados a la Royal Society en 1668. Más tarde los publicó en el Journal des Sçavans en 1669.

En 1659, Huygens encontró la constante de aceleración gravitacional y estableció lo que ahora se conoce como la segunda de las leyes del movimiento de Newton en forma cuadrática. Derivó geométricamente la fórmula ahora estándar para la fuerza centrífuga, ejercida sobre un objeto cuando se ve en un marco de referencia giratorio, por ejemplo, cuando se conduce en una curva. En notación moderna:

Fc=mw2r{displaystyle ¿Qué?

con m la masa del objeto, w la velocidad angular y r el radio. Huygens recopiló sus resultados en un tratado bajo el título De vi Centrifuga, inédito hasta 1703, donde se utilizó la cinemática de caída libre para producir la primera concepción generalizada de fuerza anterior a Newton. Sin embargo, la fórmula general para la fuerza centrífuga se publicó en 1673 y fue un paso significativo en el estudio de las órbitas en astronomía. Permitió la transición de la tercera ley del movimiento planetario de Kepler a la ley del cuadrado inverso de la gravitación. Sin embargo, la interpretación del trabajo de Newton sobre la gravitación por parte de Huygens difería de la de newtonianos como Roger Cotes: no insistió en la actitud a priori de Descartes, pero tampoco aceptaría aspectos de atracciones gravitatorias que no eran atribuibles en principio al contacto entre partículas.

El enfoque utilizado por Huygens también pasó por alto algunas nociones centrales de la física matemática, que no se perdieron en otros. En su trabajo sobre los péndulos, Huygens se acercó mucho a la teoría del movimiento armónico simple; el tema, sin embargo, fue cubierto completamente por primera vez por Newton en el Libro II de los Principia Mathematica (1687). En 1678, Leibniz extrajo del trabajo de Huygens sobre las colisiones la idea de la ley de conservación que Huygens había dejado implícita.

Relojería

Reloj de péndulo

Reloj péndulo impulsado por primavera, diseñado por Huygens y construido por Salomon Coster (1657), con una copia del Horologium Oscillatorium (1673), en Museum Boerhaave, Leiden.

En 1657, inspirado por investigaciones anteriores sobre los péndulos como mecanismos reguladores, Huygens inventó el reloj de péndulo, que supuso un gran avance en el cronometraje y se convirtió en el cronometrador más preciso durante casi 300 años hasta la década de 1930. El reloj de péndulo era mucho más preciso que los relojes de borde y foliot existentes y fue inmediatamente popular, extendiéndose rápidamente por Europa. Contrató la construcción de sus diseños de reloj a Salomon Coster en La Haya, quien construyó el reloj. Sin embargo, Huygens no ganó mucho dinero con su invento. Pierre Séguier le negó los derechos franceses, mientras que Simon Douw en Rotterdam y Ahasuerus Fromanteel en Londres copiaron su diseño en 1658. El reloj de péndulo de estilo Huygens más antiguo que se conoce data de 1657 y se puede ver en el Museo Boerhaave en Leiden.

Parte del incentivo para inventar el reloj de péndulo fue crear un cronómetro marino preciso que pudiera usarse para encontrar la longitud mediante la navegación celeste durante los viajes por mar. Sin embargo, el reloj no tuvo éxito como cronometrador marino porque el movimiento oscilante del barco perturbaba el movimiento del péndulo. En 1660, Lodewijk Huygens hizo una prueba en un viaje a España e informó que el mal tiempo inutilizaba el reloj. Alexander Bruce dio un codazo en el campo en 1662, y Huygens llamó a Sir Robert Moray y la Royal Society para mediar y preservar algunos de sus derechos. Los juicios continuaron hasta la década de 1660, y la mejor noticia provino de un capitán de la Marina Real, Robert Holmes, que operó contra las posesiones holandesas en 1664. Lisa Jardine duda de que Holmes informara con precisión los resultados del juicio, ya que Samuel Pepys expresó sus dudas en ese momento.

Un juicio para la Academia Francesa en una expedición a Cayena terminó mal. Jean Richer sugirió la corrección de la figura de la Tierra. En el momento de la expedición de la Compañía Holandesa de las Indias Orientales de 1686 al Cabo de Buena Esperanza, Huygens pudo proporcionar la corrección retrospectivamente.

Horologio Oscillatorium

Diagrama mostrando el evoluto de una curva.

Dieciséis años después de la invención del reloj de péndulo, en 1673, Huygens publicó su principal obra sobre relojería titulada Horologium Oscillatorium: Sive de Motu Pendulorum ad Horologia Aptato Demonstrationes Geometricae (El reloj de péndulo: o Demostraciones geométricas relativas al movimiento de péndulo aplicado a los relojes). Es el primer trabajo moderno sobre mecánica en el que se idealiza un problema físico mediante un conjunto de parámetros que luego se analizan matemáticamente.

La motivación de Huygens provino de la observación, realizada por Mersenne y otros, de que los péndulos no son del todo isócronos: su período depende del ancho de su oscilación, con oscilaciones anchas que tardan un poco más que las oscilaciones estrechas. Abordó este problema encontrando la curva por la que se deslizará una masa bajo la influencia de la gravedad en la misma cantidad de tiempo, independientemente de su punto de partida; el llamado problema de la tautocronía. Mediante métodos geométricos que anticiparon el cálculo, Huygens demostró que era una cicloide, en lugar del arco circular de la lenteja de un péndulo, y por lo tanto, los péndulos necesitaban moverse en una trayectoria cicloide para ser isócronos. Las matemáticas necesarias para resolver este problema llevaron a Huygens a desarrollar su teoría de las evoluciones, que presentó en la Parte III de su Horologium Oscillatorium.

También resolvió un problema planteado anteriormente por Mersenne: cómo calcular el período de un péndulo hecho de un cuerpo rígido oscilante de forma arbitraria. Esto implicó descubrir el centro de oscilación y su relación recíproca con el punto de pivote. En el mismo trabajo, analizó el péndulo cónico, que consiste en un peso sobre una cuerda que se mueve en círculo, utilizando el concepto de fuerza centrífuga.

Huygens fue el primero en derivar la fórmula para el período de un péndulo matemático ideal (con una barra o cuerda sin masa y una longitud mucho mayor que su oscilación), en notación moderna:

T=2π π lg{fnMicroc} {} {}}}}

siendo T el periodo, l la longitud del péndulo y g la aceleración de la gravedad. Mediante su estudio del período de oscilación de péndulos compuestos, Huygens hizo contribuciones fundamentales al desarrollo del concepto de momento de inercia.

Huygens también observó oscilaciones acopladas: dos de sus relojes de péndulo montados uno al lado del otro en el mismo soporte a menudo se sincronizaban, girando en direcciones opuestas. Informó los resultados por carta a la Royal Society, y se refiere a esto como "un extraño tipo de simpatía". en las actas de la Sociedad. Este concepto ahora se conoce como arrastre.

Reloj de muelle de equilibrio

Dibujo de un manantial inventado por Huygens.

En 1675, mientras investigaba las propiedades oscilantes de la cicloide, Huygens pudo transformar un péndulo cicloidal en un resorte vibrante mediante una combinación de geometría y matemáticas superiores. En el mismo año, Huygens diseñó un resorte espiral y patentó un reloj de bolsillo. Estos relojes se destacan por carecer de un fusible para igualar el par del resorte principal. La implicación es que Huygens pensó que su resorte espiral isocronizaría la balanza de la misma manera que los bordillos de suspensión en forma de cicloide en sus relojes isocronizarían el péndulo.

Más tarde usó resortes en espiral en relojes más convencionales, fabricados para él por Thuret en París. Dichos resortes son esenciales en los relojes modernos con un escape de palanca separado porque pueden ajustarse para el isocronismo. Los relojes en la época de Huygens, sin embargo, empleaban el escape de borde muy ineficaz, que interfería con las propiedades isocronales de cualquier forma de espiral, espiral o de otro tipo.

El diseño de Huygens surgió casi al mismo tiempo que el de Robert Hooke, aunque de manera independiente. La controversia sobre la prioridad del resorte de equilibrio persistió durante siglos. En febrero de 2006, se descubrió en un armario en Hampshire, Inglaterra, una copia perdida hace mucho tiempo de las notas manuscritas de Hooke de varias décadas de reuniones de la Royal Society, lo que presumiblemente inclinó la evidencia a favor de Hooke.

Óptica

Dioptría

El telescopio aéreo de Huygens Astroscopia Compendiaria (1684).

Huygens se interesó durante mucho tiempo en el estudio de la refracción de la luz y las lentes o dioptrías. De 1652 datan los primeros borradores de un tratado latino sobre la teoría de la dioptría, conocido como el Tractatus, que contenía una teoría exhaustiva y rigurosa del telescopio. Huygens fue uno de los pocos que planteó cuestiones teóricas sobre las propiedades y el funcionamiento del telescopio, y casi el único que dirigió su competencia matemática hacia los instrumentos reales utilizados en astronomía.

Huygens anunció repetidamente su publicación a sus colegas, pero finalmente la pospuso a favor de un tratamiento mucho más completo, ahora bajo el nombre de Dioptrica. Constaba de tres partes. La primera parte se centró en los principios generales de la refracción, la segunda se ocupó de la aberración esférica y cromática, mientras que la tercera cubrió todos los aspectos de la construcción de telescopios y microscopios. En contraste con Descartes' dióptrica que trataba solo lentes ideales (elípticas e hiperbólicas), Huygens se ocupó exclusivamente de lentes esféricas, que eran las únicas que realmente podían fabricarse e incorporarse en dispositivos como microscopios y telescopios.

Huygens también ideó formas prácticas de minimizar los efectos de la aberración esférica y cromática, como largas distancias focales para el objetivo de un telescopio, topes internos para reducir la apertura y un nuevo tipo de ocular en forma de conjunto. de dos lentes planoconvexas, ahora conocido como el ocular de Huygens. La Dioptrica nunca se publicó en vida de Huygens y solo apareció en prensa en 1703, cuando la mayor parte de su contenido ya era familiar para el mundo científico.

Lentes

Junto con su hermano Constantijn, Huygens comenzó a moler sus propias lentes en 1655 en un esfuerzo por mejorar los telescopios. Diseñó en 1662 lo que ahora se llama el ocular Huygenian, con dos lentes, como un telescopio ocular. Las lentes también fueron un interés común a través del cual Huygens pudo reunirse socialmente en la década de 1660 con Spinoza, quien las cimentó profesionalmente. Tenían puntos de vista bastante diferentes sobre la ciencia, siendo Spinoza el cartesiano más comprometido, y parte de su discusión sobrevive en la correspondencia. Se encontró con el trabajo de Antoni van Leeuwenhoek, otro pulidor de lentes, en el campo de la microscopía que interesó a su padre.

Huygens también investigó el uso de lentes en proyectores. Se le acredita como el inventor de la linterna mágica, descrita en una correspondencia de 1659. Hay otros a quienes se les ha atribuido un dispositivo de linterna de este tipo, como Giambattista della Porta y Cornelis Drebbel, aunque el diseño de Huygens usó lentes para mejorar. proyección (Athanasius Kircher también ha sido acreditado por eso).

Traité de la Lumiere

Reflexión de una ola de avión, explicado usando el principio de Huygens en Traité de la Lumière (1690).

Huygens es especialmente recordado en óptica por su teoría ondulatoria de la luz, que comunicó por primera vez en 1678 a la Académie des sciences de París. Originalmente un capítulo preliminar de su Dioptrica, la teoría de Huygens se publicó en 1690 con el título Traité de la Lumière (Tratado sobre la luz).), y contiene la primera explicación mecanicista completamente matemática de un fenómeno físico no observable (es decir, la propagación de la luz). Huygens se refiere a Ignace-Gaston Pardies, cuyo manuscrito sobre óptica lo ayudó en su teoría ondulatoria.

El desafío en ese momento era explicar la óptica geométrica, ya que la mayoría de los fenómenos de la óptica física (como la difracción) no se habían observado ni apreciado como problemas. Huygens había experimentado en 1672 con la doble refracción (birrefringencia) en el espato de Islandia (una calcita), un fenómeno descubierto en 1669 por Rasmus Bartholin. Al principio, no pudo dilucidar lo que encontró, pero luego pudo explicarlo utilizando su teoría del frente de onda y el concepto de evolución. También desarrolló ideas sobre cáusticos. Huygens asume que la velocidad de la luz es finita, basándose en un informe de Ole Christensen Rømer de 1677 pero que se presume que Huygens ya creía. La teoría de Huygens postula la luz como frentes de onda radiantes, con la noción común de rayos de luz que representan la propagación normal a esos frentes de onda. La propagación de los frentes de onda se explica entonces como el resultado de la emisión de ondas esféricas en cada punto a lo largo del frente de onda (conocido hoy como el principio de Huygens-Fresnel). Asumió un éter omnipresente, con transmisión a través de partículas perfectamente elásticas, una revisión de la visión de Descartes. La naturaleza de la luz era, por tanto, una onda longitudinal.

Su teoría de la luz no fue ampliamente aceptada, mientras que la teoría corpuscular rival de la luz de Newton, como se encuentra en su Óptica (1704), ganó más apoyo. Una fuerte objeción a la teoría de Huygens fue que las ondas longitudinales tienen una sola polarización que no puede explicar la birrefringencia observada. Sin embargo, los experimentos de interferencia de Thomas Young en 1801 y la detección de la mancha de Poisson por parte de François Arago en 1819 no pudieron explicarse a través de la teoría de partículas de Newton ni de ninguna otra, reviviendo la teoría de Huygens. ideas y modelos de ondas. Fresnel se dio cuenta del trabajo de Huygens y en 1821 pudo explicar la birrefringencia como resultado de que la luz no es una onda longitudinal (como se suponía) sino transversal. El así llamado principio de Huygens-Fresnel fue la base para el avance de la óptica física, explicando todos los aspectos de la propagación de la luz hasta que la teoría electromagnética de Maxwell culminó con el desarrollo de la mecánica cuántica y el descubrimiento del fotón.

Astronomía

Sistema Saturnio

La explicación de Huygens sobre los aspectos de Saturno, Systema Saturnium (1659).

En 1655, Huygens descubrió la primera de las lunas de Saturno, Titán, y observó y dibujó la Nebulosa de Orión utilizando un telescopio refractor con un aumento de 43x diseñado por él mismo. Huygens logró subdividir la nebulosa en diferentes estrellas (el interior más brillante ahora lleva el nombre de región huygeniana en su honor), y descubrió varias nebulosas interestelares y algunas estrellas dobles. También fue el primero en proponer que la apariencia de Saturno, que desconcertó a los astrónomos, se debía a "un anillo delgado y plano, que no se tocaba en ninguna parte e inclinado hacia la eclíptica".

Más de tres años después, en 1659, Huygens publicó su teoría y hallazgos en Systema Saturnium. Se considera el trabajo más importante sobre astronomía telescópica desde el Sidereus Nuncius de Galileo cincuenta años antes. Mucho más que un informe sobre Saturno, Huygens proporcionó medidas de las distancias relativas de los planetas al Sol, introdujo el concepto del micrómetro y mostró un método para medir los diámetros angulares de los planetas, lo que finalmente permitió que el telescopio se usara como un instrumento para medir (en lugar de solo observar) objetos astronómicos. También fue el primero en cuestionar la autoridad de Galileo en materia telescópica, un sentimiento que sería común en los años posteriores a su publicación.

En el mismo año, Huygens pudo observar Syrtis Major, una llanura volcánica en Marte. Usó observaciones repetidas del movimiento de esta característica en el transcurso de varios días para estimar la duración del día en Marte, lo que hizo con bastante precisión en 24 1/2 horas. Esta cifra está a solo unos minutos de la duración real del día marciano de 24 horas y 37 minutos.

Planetario

A instancias de Jean-Baptiste Colbert, Huygens emprendió la tarea de construir un planetario mecánico que pudiera mostrar todos los planetas y sus lunas conocidos entonces girando alrededor del Sol. Huygens completó su diseño en 1680 e hizo que su relojero Johannes van Ceulen lo construyera al año siguiente. Sin embargo, Colbert falleció mientras tanto y Huygens nunca pudo entregar su planetario a la Academia de Ciencias de Francia ya que el nuevo ministro, François-Michel le Tellier, decidió no renovar el contrato de Huygens.

En su diseño, Huygens hizo un uso ingenioso de las fracciones continuas para encontrar las mejores aproximaciones racionales mediante las cuales pudiera elegir los engranajes con el número correcto de dientes. La relación entre dos engranajes determinó los períodos orbitales de dos planetas. Para mover los planetas alrededor del Sol, Huygens usó un mecanismo de reloj que podía avanzar y retroceder en el tiempo. Huygens afirmó que su planetario era más preciso que un dispositivo similar construido por Ole Rømer en la misma época, pero su diseño de planetario no se publicó hasta después de su muerte en el Opuscula Posthuma (1703).

Cosmoteoros

Tamaños relativos del Sol y planetas en Cosmotheoros (1698).

Poco antes de su muerte en 1695, Huygens completó su obra más especulativa titulada Cosmotheoros. Bajo su dirección, su hermano lo publicaría solo póstumamente, lo que Constantijn Jr. hizo en 1698. En este trabajo, Huygens especuló sobre la existencia de vida extraterrestre, que imaginó similar a la de la Tierra. Tales especulaciones no eran infrecuentes en ese momento, justificadas por el copernicanismo o el principio de plenitud, pero Huygens entró en más detalles. Sin embargo, lo hizo sin el beneficio de comprender las leyes de gravitación de Newton, o el hecho de que las atmósferas de otros planetas están compuestas de diferentes gases. Cosmotheoros, traducido al inglés como Los mundos celestiales descubiertos, ha sido visto como parte de la ficción especulativa en la tradición de Francis Godwin, John Wilkins y Cyrano de Bergerac. El trabajo de Huygens fue fundamentalmente utópico y debe algo de inspiración en la cosmografía y la especulación planetaria de Peter Heylin.

Huygens escribió que la disponibilidad de agua en forma líquida era esencial para la vida y que las propiedades del agua deben variar de un planeta a otro para adaptarse al rango de temperatura. Tomó sus observaciones de puntos oscuros y brillantes en las superficies de Marte y Júpiter como evidencia de agua y hielo en esos planetas. Argumentó que la Biblia no confirma ni niega la vida extraterrestre, y cuestionó por qué Dios crearía los otros planetas si no tuvieran un propósito mayor que el de ser admirados desde la Tierra. Huygens postuló que la gran distancia entre los planetas significaba que Dios no tenía la intención de que los seres de uno supieran sobre los seres de los otros, y no había previsto cuánto avanzarían los humanos en el conocimiento científico.

También fue en este libro que Huygens publicó sus estimaciones de los tamaños relativos del sistema solar y su método para calcular las distancias estelares. Hizo una serie de agujeros más pequeños en una pantalla frente al Sol, hasta que estimó que la luz era de la misma intensidad que la de la estrella Sirio. Luego calculó que el ángulo de este agujero era 1/27.664 del diámetro del Sol y, por lo tanto, estaba unas 30.000 veces más lejos, con la suposición (incorrecta) de que Sirio es tan luminoso como el Sol. El tema de la fotometría permaneció en su infancia hasta la época de Pierre Bouguer y Johann Heinrich Lambert.

Legado

Durante su vida, la influencia de Huygens fue considerable, pero comenzó a desvanecerse poco después de su muerte. Sus habilidades como geómetra y sus conocimientos mecánicos provocaron la admiración de muchos de sus contemporáneos, incluidos Newton, Leibniz, l'Hôpital y los Bernoulli. Por su trabajo en física, Huygens ha sido considerado uno de los más grandes científicos de la Europa del siglo XVII y una figura prominente en la Revolución Científica, rivalizado solo por Newton tanto en profundidad de conocimiento como en el número de resultados obtenidos. Huygens también ayudó a desarrollar los marcos institucionales para la investigación científica en el continente europeo, lo que lo convirtió en un actor principal en el establecimiento de la ciencia moderna.

Matemáticas y física

Retrato de Christiaan Huygens de Bernard Vaillant (1686).

En matemáticas, Huygens dominó los métodos de la geometría griega antigua, particularmente el trabajo de Arquímedes, y fue un experto usuario de la geometría analítica y las técnicas infinitesimales de Descartes, Fermat y otros. Su estilo matemático se puede caracterizar como análisis infinitesimal geométrico de curvas y de movimiento. Inspirándose e imaginando en la mecánica, siguió siendo matemática pura en su forma. Huygens puso fin a este tipo de análisis geométrico, ya que más matemáticos se apartaron de la geometría clásica y se dirigieron al cálculo para manejar los infinitesimales, los procesos límite y el movimiento.

Además, Huygens pudo emplear completamente las matemáticas para responder preguntas de física. A menudo, esto implicó introducir un modelo simple para describir una situación complicada, luego analizarlo a partir de argumentos simples hasta sus consecuencias lógicas, desarrollando las matemáticas necesarias en el camino. Como escribió al final de un borrador de De vi Centrifuga:

Cualquier cosa que se supone que no es imposible ya sea respecto a la gravedad o movimiento o cualquier otra materia, si entonces usted prueba algo concerniente a la magnitud de una línea, superficie o cuerpo, será verdad; como por ejemplo, Arquímedes en la cuadratura de la parabola, donde se ha asumido la tendencia de objetos pesados a actuar a través de líneas paralelas.

Huygens favoreció las presentaciones axiomáticas de sus resultados, que requieren métodos rigurosos de demostración geométrica: aunque permitió niveles de incertidumbre en la selección de axiomas e hipótesis primarios, las pruebas de los teoremas derivados de estos nunca podrían estar en duda. El estilo de publicación de Huygens ejerció una influencia en la presentación de Newton de sus propias obras principales.

Además de la aplicación de las matemáticas a la física y de la física a las matemáticas, Huygens se basó en las matemáticas como metodología, particularmente en su capacidad para generar nuevos conocimientos sobre el mundo. A diferencia de Galileo, que usó las matemáticas principalmente como retórica o síntesis, Huygens empleó consistentemente las matemáticas como un método de descubrimiento y análisis, e insistió en que la reducción de lo físico a lo geométrico satisfizo los exigentes estándares de ajuste entre lo real y lo ideal. Al exigir tal maleabilidad y precisión matemática, Huygens sentó un ejemplo para científicos del siglo XVIII como Johann Bernoulli, Jean le Rond d'Alembert y Charles-Augustin de Coulomb.

Aunque nunca tuvo la intención de publicarse, Huygens utilizó expresiones algebraicas para representar entidades físicas en algunos de sus manuscritos sobre colisiones. Esto lo convertiría en uno de los primeros en emplear fórmulas matemáticas para describir las relaciones en la física, como se hace hoy. Huygens también se acercó a la idea moderna de límite mientras trabajaba en su Dioptrica, aunque nunca utilizó la noción fuera de la óptica geométrica.

Influencia posterior

La posición de Huygens como el científico más grande de Europa fue eclipsada por la de Newton a fines del siglo XVII, a pesar de que, como señala Hugh Aldersey-Williams, 'Huygens' Su logro supera al de Newton en algunos aspectos importantes. Su estilo muy idiosincrático y su renuencia a publicar su trabajo contribuyeron en gran medida a disminuir su influencia después de la Revolución Científica, cuando los seguidores del cálculo de Leibniz y la física de Newton ocuparon un lugar central.

Los análisis de Huygens de curvas que satisfacen ciertas propiedades físicas, como la cicloide, llevaron a estudios posteriores de muchas otras curvas como la cáustica, la braquistocrona, la curva de vela y la catenaria. Su aplicación de las matemáticas a la física, como en su estudio de la birrefringencia, inspiraría nuevos desarrollos en la física matemática y la mecánica racional en los siglos siguientes (aunque en el nuevo lenguaje del cálculo). Además, Huygens desarrolló los mecanismos de cronometraje oscilantes, el péndulo y el resorte de equilibrio, que se han utilizado desde entonces en los relojes mecánicos. Estos fueron los primeros cronometradores confiables aptos para uso científico (por ejemplo, fue posible por primera vez hacer mediciones precisas de la desigualdad del día solar, lo que los astrónomos en el pasado no podían hacer). Su trabajo en esta área anticipó la unión de las matemáticas aplicadas con la ingeniería mecánica en los siglos siguientes.

Retratos

Durante su vida, Huygens y su padre encargaron una serie de retratos. Estos incluyeron:

• 1639 – Constantijn Huygens en medio de sus cinco hijos por Adriaen Hanneman, pintura con medallones, Mauritshuis, La Haya
• 1671 – Retrato de Caspar Netscher, Museum Boerhaave, Leiden, préstamo del Museo Haags Historisch
• c.1675 – Depiction of Huygens in Établissement de l'Académie des Sciences et fondation de l'observatoire, 1666 por Henri Testelin. Colbert presenta a los miembros de la recién fundada Académie des Sciences al rey Luis XIV de Francia. Musée National du Château et des Trianons de Versailles, Versailles
• 1679 – Retrato de Medaillon en relieve por el escultor francés Jean-Jacques Clérion
• 1686 – Retrato en pastel de Bernard Vaillant, Museo Hofwijck, Voorburg
• 1684 a 1687 – Grabados por G. Edelinck después de la pintura de Caspar Netscher
• 1688 – Retrato de Pierre Bourguignon (interés), Real Academia de Artes y Ciencias de Holanda, Amsterdam

Conmemoraciones

La nave espacial de la Agencia Espacial Europea que aterrizó en Titán, la luna más grande de Saturno, en 2005 lleva su nombre.

Se pueden encontrar varios monumentos a Christiaan Huygens en ciudades importantes de los Países Bajos, como Róterdam, Delft y Leiden.

• 

  Rotterdam

• 

  Delft

• 

  Leiden

• 

  Haarlem

• 

  Voorburg

Obras

Título página de Oeuvres Complètes I

Fuente(s):

• 1650 – De Iis Quae Liquido Supernatant ()Sobre partes flotando sobre líquidos, inédito).
• 1651 – Theoremata de Quadratura Hyperboles, Ellipsis et Circuli, republished in Oeuvres Complètes, Tome XI.
• 1651 – Epistola, qua diluuntur ea quibus 'Ε► Conceptτασς [Exetasis] Cyclometriae Gregori à Sto. Vincentio impugnata fuit (suplemento).
• 1654 – De Circuli Magnitudine Inventa.
• 1654 – Illustrium Quorundam Construcciones problemáticas (suplemento).
• 1655 – Horologium ()El reloj – panfleto corto en el reloj péndulo).
• 1656 – De Saturni Luna Observatio Nova ()Sobre la nueva observación de la luna de Saturno, describir el descubrimiento de Titan).
• 1656 – De Motu Corporum ex Percussione, publicado póstumamente en 1703.
• 1657 – De Ratiociniis en Ludo Aleae ()Van reeckening in spelen van geluck, traducido al latín por Frans van Schooten).
• 1659 – Systema Saturnium ()Sistema de Saturno).
• 1659 – De vi Centrifuga ()Con respecto a la fuerza centrífuga), publicado póstumamente en 1703.
• 1673 – Horologium Oscillatorium Sive de Motu Pendulorum ad Horologia Aptato Demonstrationes Geometricae (incluye su teoría de evolutes y diseños de relojes de péndulo, dedicado a Luis XIV de Francia).
• 1684 – Astroscopia Compendiaria Tubi Optici Molimine Liberata ()telescopios compuestos sin tubo).
• 1685 – Memoriën aengaende het slijpen van glasen tot verrekijckers (muerto con la molienda de las lentes).
• 1686 – Viejo holandés: Kort onderwijs aengaende het gebruijck der horologiën tot het vinden der lenghten van Oost en West (instrucción sobre cómo utilizar relojes para establecer la longitud en el mar).
• 1690 – Traité de la Lumière (Dealar con la naturaleza de la propagación de la luz).
• 1690 – Discours de la Causa de la Pesanteur ()Discurso sobre la gravedad, suplemento).
• 1691 – Lettre Touchant le Cycle Harmonique (página corta relativa al sistema de 31 toneladas).
• 1698 – Cosmotheoros (realización con el sistema solar, cosmología y vida extraterrestre).
• 1703 – Opuscula Posthuma incluido:
  • De Motu Corporum ex Percussione ()En cuanto a las mociones de los órganos de colisión, contiene las primeras leyes correctas para la colisión, que datan de 1656).
  • Descriptio Automati Planetarii (descripción y diseño de un planetario).
• 1724 – Novus Cyclus Harmonicus (un tratado sobre la música, publicado en Leiden después de la muerte de Huygens).
• 1728 – Christiani Hugenii Zuilichemii, dum viveret Zelhemii Toparchae, Opuscula Posthuma... (pub. 1728) Título suplente: Opera Reliqua, incluyendo trabajos en óptica y física
• 1888-1950 – Huygens, Christiaan. Oeuvres complètes. Obras completas, 22 volúmenes. Editores D. Bierens de Haan (1–5), J. Bosscha (6–10), D.J. Korteweg (11–15), A.A. Nijland (15), J.A. Vollgraf (16–22). La Haya:
  • Tomé I: Correspondencia 1638-1656 (1888).
  • Tomé II: Correspondencia 1657-1659 (1889).
  • Tomé III: Correspondencia 1660-1661 (1890).
  • Tomé IV: Correspondencia 1662-1663 (1891).
  • Tomé V: Correspondencia 1664-1665 (1893).
  • Tomé VI: Correspondencia 1666-1669 (1895).
  • Tomé VII: Correspondencia 1670-1675 (1897).
  • Tomé VIII: Correspondencia 1676-1684 (1899).
  • Tomé IX: Correspondencia 1685-1690 (1901).
  • Tomé X: Correspondencia 1691-1695 (1905).
  • Tomé XI: Travaux mathématiques 1645-1651 (1908).
  • Tomé XII: Travaux mathématiques purs 1652-1656 (1910).
  • Tome XIII, Fasc. I: Dioptrique 1653, 1666 (1916).
  • Tome XIII, Fasc. II: Dioptrique 1685-1692 (1916).
  • Tome XIV: Calcul des probabilités. Travaux de mathématiques purs 1655-1666 (1920).
  • Tome XV: Observaciones astronómicas. Système de Saturne. Travaux astronomiques 1658-1666 (1925).
  • Tome XVI: Mécanique jusqu’à 1666. Percusión. Pregunta de l'existence et de la perceptibilité du mouvement absolu. Centrifugado de fuerza (1929).
  • Tome XVII: L’horloge à pendule de 1651 à 1666. Travaux divers de physique, de mécanique et de technique de 1650 à 1666. Traité des couronnes et des parhélies (1662 ou 1663) (1932).
  • Tome XVIII: L'horloge à pendule ou à balancier de 1666 à 1695. Anecdota (1934).
  • Tome XIX: Mécanique théorique et physique de 1666 à 1695. Huygens à l'Académie royale des sciences (1937).
  • Tome XX: Musique et mathématique. Musique. Mathématiques de 1666 à 1695 (1940).
  • Tome XXI: Cosmologie (1944).
  • Tome XXII: Supplément à la correspondance. Varia. Biographie de Chr. Huygens. Catalogue de la vente des livres de Chr. Huygens (1950).