Coordenadas parabólicas

coordenadas parabólicas son un sistema de coordenadas ortogonales bidimensionales en el que las líneas de coordenadas son parábolas confocales. Se obtiene una versión tridimensional de las coordenadas parabólicas girando el sistema bidimensional alrededor del eje de simetría de las parábolas.

Las coordenadas parabólicas han encontrado muchas aplicaciones, por ejemplo, el tratamiento del efecto Stark y la teoría potencial de los bordes.

Coordenadas parabólicas bidimensionales

Coordenadas parabólicas bidimensionales ()σ σ ,τ τ ){displaystyle (sigmatau)} son definidos por las ecuaciones, en términos de coordenadas cartesianas:

x=σ σ τ τ {displaystyle x=sigma tau }

Sí.=12()τ τ 2− − σ σ 2){displaystyle y={2}left(tau ^{2}-sigma ^{2}right)}

Las curvas de constante σ σ {displaystyle sigma } form confocal parabolae

2Sí.=x2σ σ 2− − σ σ 2{displaystyle 2y={frac {x^{2}{sigma ^{2}sigma ^{2}}

que se abre hacia arriba (es decir, hacia +Sí.{displaystyle #), mientras que las curvas de constante τ τ {displaystyle tau } form confocal parabolae

2Sí.=− − x2τ τ 2+τ τ 2{displaystyle 2y=-{frac {x^{2}{tau ^{2}}+tau ^{2}}

que se abre hacia abajo (es decir, hacia − − Sí.{displaystyle - Sí.). El foci de todos estos parabolaos se encuentran en el origen.

Las coordenadas cartesianas x{displaystyle x} y Sí.{displaystyle y} se puede convertir en coordenadas parabólicas por:

σ σ =Signatura⁡ ⁡ ()x)x2+Sí.2− − Sí.{displaystyle sigma =operatorname {sign} (x){sqrt {sqrt {x^{2}+y^{2}}-y}}

τ τ =x2+Sí.2+Sí.{displaystyle tau ={sqrt {sqrt {x^{2}+y}}}

Factores de escala bidimensional

Los factores de escala para las coordenadas parabólicas ()σ σ ,τ τ ){displaystyle (sigmatau)} son iguales

hσ σ =hτ τ =σ σ 2+τ τ 2{displaystyle h_{sigma }=h_{tau }={2}}}

Por lo tanto, el elemento infinitesimal del área es

dA=()σ σ 2+τ τ 2)dσ σ dτ τ {displaystyle dA=left(sigma ^{2}+tau ^{2}right)dsigma dtau }

y el laplaciano es igual

Silencio Silencio 2CCPR CCPR =1σ σ 2+τ τ 2()∂ ∂ 2CCPR CCPR ∂ ∂ σ σ 2+∂ ∂ 2CCPR CCPR ∂ ∂ τ τ 2){displaystyle nabla ^{2} Phi ={frac {1}{sigma ^{2}+tau ^{2}left({frac {partial ^{2} Phi }{partial sigma ^{2}}}+{frac {partial ^{2} Phi }{partial tau ^{2}}right)}

Otros operadores diferenciales como Silencio Silencio ⋅ ⋅ F{displaystyle nabla cdot mathbf {F} y Silencio Silencio × × F{displaystyle nabla times mathbf {F} se puede expresar en las coordenadas ()σ σ ,τ τ ){displaystyle (sigmatau)} por sustitución los factores de escala en la fórmula general encontrado en coordenadas ortogonales.

Coordenadas parabólicas tridimensionales

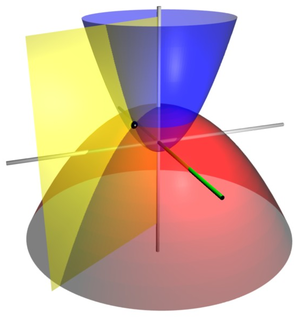
Las coordenadas parabólicas bidimensionales forman la base para dos conjuntos de coordenadas ortogonales tridimensionales. Las coordenadas cilíndricas parabólicas se producen proyectando en el z{displaystyle z}- dirección. La rotación sobre el eje simétrico de la parabola produce un conjunto de paraboloides confocales, el sistema de coordinación de coordenadas parabólicas tridimensionales. Expresado en términos de coordenadas cartesianas:

x=σ σ τ τ #⁡ ⁡ φ φ {displaystyle x=sigma tau cos varphi }

Sí.=σ σ τ τ pecado⁡ ⁡ φ φ {displaystyle y=sigma tau sin varphi }

z=12()τ τ 2− − σ σ 2){displaystyle z={2}left(tau ^{2}-sigma ^{2}right)}

donde el parabolao está ahora alineado con el z{displaystyle z}- Eje, sobre el cual se realizó la rotación. Por lo tanto, el ángulo azimutal φ φ {displaystyle phi } se define

#⁡ ⁡ φ φ =Sí.x{displaystyle tan varphi = {y}{x}}

Las superficies de constante σ σ {displaystyle sigma } form confocal paraboloids

2z=x2+Sí.2σ σ 2− − σ σ 2{displaystyle 2z={frac {x^{2}+y^{2} {sigma }}-sigma ^{2}}

que se abre hacia arriba (es decir, hacia +z{displaystyle +z}) mientras que las superficies de constante τ τ {displaystyle tau } form confocal paraboloids

2z=− − x2+Sí.2τ τ 2+τ τ 2{displaystyle 2z=-{frac {x^{2}+y^{2} {tau }}+tau ^{2}}}}} {tau

que se abre hacia abajo (es decir, hacia − − z{displaystyle -z}). El foci de todos estos paraboloides se encuentra en el origen.

El tensor métrico de Riemann asociado con este sistema de coordenadas es

gij=[σ σ 2+τ τ 2000σ σ 2+τ τ 2000σ σ 2τ τ 2]{displaystyle g_{ij}={begin{bmatrix}sigma ^{2}+tau ################################################################################################################################################################################################################################################################ ^{2} {2}end{bmatrix}}

Factores de escala tridimensional

Los factores de escala tridimensionales son:

hσ σ =σ σ 2+τ τ 2{displaystyle h_{sigma }={2}}}

hτ τ =σ σ 2+τ τ 2{displaystyle h_{tau }={2}}}

hφ φ =σ σ τ τ {displaystyle h_{varphi }=sigma tau }

Se ve que los factores de escala hσ σ {displaystyle ¿Qué? y hτ τ {displaystyle h_{tau } son los mismos que en el caso bidimensional. El elemento de volumen infinitesimal es entonces

dV=hσ σ hτ τ hφ φ dσ σ dτ τ dφ φ =σ σ τ τ ()σ σ 2+τ τ 2)dσ σ dτ τ dφ φ {displaystyle DV=h_{sigma.. },dsigma ,dtau ,dvarphi =sigma tau left(sigma ^{2}+tau ^{2}right),dsigma ,dtau ,dvarphi }

y el laplaciano viene dado por

Silencio Silencio 2CCPR CCPR =1σ σ 2+τ τ 2[1σ σ ∂ ∂ ∂ ∂ σ σ ()σ σ ∂ ∂ CCPR CCPR ∂ ∂ σ σ )+1τ τ ∂ ∂ ∂ ∂ τ τ ()τ τ ∂ ∂ CCPR CCPR ∂ ∂ τ τ )]+1σ σ 2τ τ 2∂ ∂ 2CCPR CCPR ∂ ∂ φ φ 2{displaystyle nabla ^{2} Phi ={frac {1}{sigma ^{2}+tau ^{2}}left[{frac {1}{sigma }{frac {partial }{sigma }left(sigma {frac {partial {partial }} {sigma }}}}left(sigma {sigma {sigma {sigma {sigma {sigma {sigma {sigma {sigma {sigma {sigma {sigma {sigma {f}}\f}sigma {fc}f}f}fcfcfcfc {fcf}fcf}fcfc}f}f}f}fc}fcsigma {fcfcfcf}f}fc {fnK} {fnMicrosoft} {fnMicrosoft} {fnMicrosoft} {f} {fncipal}} {fncipal}}}} {fnMicrosoft {fnMicrosoft {fnMicrosoft}}} {f}}}}}}}fnMicroc} {f}}}}} {f}f} {f}f}}}}}}f}}}f}f}}f}f}f}}f}f}f}f}f}f}f}f}f}f}f}f}f} {f} {f} {f} {f}f}f} {f}f}f}f} {f}f}}f}f}f}f}f}f}f}f}f}f}f

Otros operadores diferenciales como Silencio Silencio ⋅ ⋅ F{displaystyle nabla cdot mathbf {F} y Silencio Silencio × × F{displaystyle nabla times mathbf {F} se puede expresar en las coordenadas ()σ σ ,τ τ ,φ φ ){displaystyle (sigmatauphi)} por sustitución los factores de escala en la fórmula general encontrado en coordenadas ortogonales.