Coordenadas curvilíneas

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

**Curvilinear** (top), affine (right), and Cartesian (left) coordinates in two-dimensional space

En geometría, las coordenadas curvilíneas son un sistema de coordenadas para el espacio euclidiano en el que las líneas de coordenadas pueden ser curvas. Estas coordenadas pueden derivarse de un conjunto de coordenadas cartesianas mediante el uso de una transformación que es localmente invertible (un mapa uno a uno) en cada punto. Esto significa que se puede convertir un punto dado en un sistema de coordenadas cartesiano a sus coordenadas curvilíneas y viceversa. El nombre coordenadas curvilíneas, acuñado por el matemático francés Lamé, deriva del hecho de que las superficies de coordenadas de los sistemas curvilíneos son curvas.

Ejemplos bien conocidos de sistemas de coordenadas curvilíneas en el espacio euclidiano tridimensional (R³) son las coordenadas cilíndricas y esféricas. Una superficie de coordenadas cartesianas en este espacio es un plano de coordenadas; por ejemplo, z = 0 define el plano x-y. En el mismo espacio, la superficie de coordenadas r = 1 en coordenadas esféricas es la superficie de una esfera unitaria, que es curva. El formalismo de coordenadas curvilíneas proporciona una descripción general y unificada de los sistemas de coordenadas estándar.

Las coordenadas curvilíneas se utilizan a menudo para definir la ubicación o distribución de cantidades físicas que pueden ser, por ejemplo, escalares, vectores o tensores. Las expresiones matemáticas que involucran estas cantidades en el cálculo vectorial y el análisis de tensores (como el gradiente, la divergencia, la curvatura y el laplaciano) se pueden transformar de un sistema de coordenadas a otro, de acuerdo con las reglas de transformación para escalares, vectores y tensores. Estas expresiones se vuelven válidas para cualquier sistema de coordenadas curvilíneo.

Un sistema de coordenadas curvilíneo puede ser más sencillo de usar que el sistema de coordenadas cartesiano para algunas aplicaciones. El movimiento de partículas bajo la influencia de fuerzas centrales suele ser más fácil de resolver en coordenadas esféricas que en coordenadas cartesianas; esto es cierto para muchos problemas físicos con simetría esférica definidos en R³. Las ecuaciones con condiciones de contorno que siguen superficies de coordenadas para un sistema de coordenadas curvilíneo particular pueden ser más fáciles de resolver en ese sistema. Si bien se podría describir el movimiento de una partícula en una caja rectangular usando coordenadas cartesianas, es más fácil describir el movimiento en una esfera con coordenadas esféricas. Las coordenadas esféricas son los sistemas de coordenadas curvilíneas más comunes y se utilizan en ciencias de la Tierra, cartografía, mecánica cuántica, relatividad e ingeniería.

Coordenadas curvilíneas ortogonales en 3 dimensiones

Coordenadas, bases y vectores

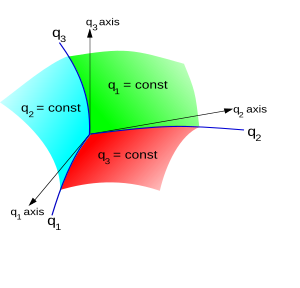
Por ahora, considere el espacio 3-D. Un punto P en el espacio 3-D (o su vector de posición r) se puede definir utilizando coordenadas cartesianas (x, Sí., z[Equivalentemente escrito (x¹, x², x³) ${displaystyle mathbf {r} =xmathbf {e} ¿Qué? ¿Qué?$ , donde e_x, e_Sí., e_z son vectores de base estándar.

También puede definirse por sus coordenadas curvilíneas (q¹, q^{2, q³) si este triplete de números define un único punto de forma inequívoca. La relación entre las coordenadas viene dada por las funciones de transformación reversibles:}

{displaystyle x=f^{1}(q^{1},q^{2},q^{3}),,y=f^{2}(q^{1},q^{2},q^{3}),,z=f^{3}(q^{1},q^{2})}

{displaystyle q^{1}=g^{1}(x,y,z),,q^{2}=g^{2}(x,y,z),,q^{3}=g^{3}(x,y,z)}

Las superficies q¹ = constante, q² = constante, q³ = constante se denominan superficies de coordenadas; y las curvas espaciales formadas por su intersección en pares se llaman curvas de coordenadas. Los ejes de coordenadas están determinados por las tangentes a las curvas de coordenadas en la intersección de tres superficies. En general, no son direcciones fijas en el espacio, como ocurre con las coordenadas cartesianas simples y, por lo tanto, generalmente no existe una base global natural para las coordenadas curvilíneas.

En el sistema cartesiano, los vectores de base estándar se pueden derivar de la derivada de la ubicación del punto P con respecto a la coordenada local.

{displaystyle mathbf {e} {fnMicrosoft Sans Serif} }{partial - ¿Qué? {fnMicrosoft Sans Serif} }{partial - Sí. {fnMicrosoft Sans Serif} } {partial z}}

Aplicar las mismas derivadas al sistema curvilíneo localmente en el punto P define los vectores de base natural:

{displaystyle mathbf {h} _{1}={dfrac {partial mathbf {r}{partial q^{1}}}}};;mathbf {h} {fnK} {fnMitbf} {f}}};;mthbf {h} {fnMicroc {fnMithbf {r}{partial q^{3}}}}

Esta base, cuyos vectores cambian su dirección y/o magnitud de un punto a otro, se denomina base local. Todas las bases asociadas con coordenadas curvilíneas son necesariamente locales. Los vectores base que son iguales en todos los puntos son bases globales y sólo pueden asociarse con sistemas de coordenadas lineales o afines.

Para este artículo e está reservado para la base estándar (cartesiana) y h o b es para la base curvilínea.

Es posible que no tengan una unidad de longitud y que tampoco sean ortogonales. En el caso de que son ortogonales en todos los puntos donde las derivadas están bien definidas, definimos los coeficientes de Lamé (después de Gabriel Lamé) por

{displaystyle h_{1}=vivirmathbf {h} _{1}tuvo;;h_{2} ¿Qué?

y los vectores de base ortonormal curvilínea por

{displaystyle mathbf {b} ¿Qué? - No. {b} ¿Qué? {fnMitbf} ¿Qué? ¿Qué? {fnMitbf} - Sí.

Estos vectores de base bien pueden depender de la posición de P; por lo tanto, es necesario que no se supone que sean constantes sobre una región. (Técnicamente forman una base para el conjunto tangente de ${displaystyle mathbb {R} } {}} {}displaystyle mathbb {R} }$ a P, y también son locales P)

En general, las coordenadas curvilíneas permiten que los vectores de base naturales h_i no sean todos mutuamente perpendiculares entre sí y no es necesario que tengan una longitud unitaria: pueden ser de magnitud y dirección arbitrarias. El uso de una base ortogonal hace que las manipulaciones vectoriales sean más sencillas que las no ortogonales. Sin embargo, algunas áreas de la física y la ingeniería, particularmente la mecánica de fluidos y la mecánica continua, requieren bases no ortogonales para describir las deformaciones y el transporte de fluidos para tener en cuenta las complicadas dependencias direccionales de las cantidades físicas. Una discusión del caso general aparece más adelante en esta página.

Cálculo vectorial

Elementos diferenciales

En coordenadas curvilíneas ortogonales, dado que el cambio diferencial total en r es

{displaystyle dmathbf} ={dfrac {partial mathbf {r} }{partial q^{1}dq^{1}+{dfrac {partial mathbf {r} }{partial - ¿Qué? {fnMitbf} {fnMitbf} {fnMitbf} {f} {fnMitbf} {f}}} {fnMicrosoft}} {fnMicrosoft}}} {cH}} {fnMicrosoft}}}} {fnMicrosoft} - ¿Qué? {b} ¿Qué? ¿Qué? ¿Qué?

así que los factores de escala ${displaystyle h_{i}=left forever{frac {partial mathbf {r} {fnMicrosoft Sans Serif}$

En no ortogonal coordina la longitud de ${displaystyle dmathbf} =dq^{1}mathbf {h} ¿Qué? ¿Qué? ¿Qué?$ es la raíz cuadrada positiva ${displaystyle dmathbf {r} cdot dmathbf {r} - ¿Sí?$ (con la convención de sumación de Einstein). Los seis productos de escalar independientes g_ij=h_i.h_j de la base natural vectores generalizar los tres factores de escala definidos anteriormente para coordenadas ortogonales. Los nueve g_ij son los componentes del tensor métrico, que tiene sólo tres componentes no cero en las coordenadas ortogonales: g₁₁=h₁h₁, g₂₂=h₂h₂, g₃₃=h₃h₃.

Bases covariantes y contravariantes

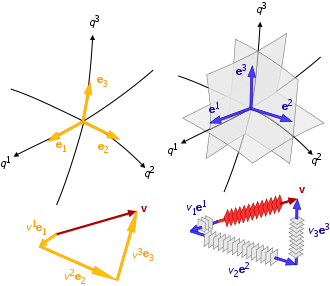
Los gradientes espaciales, las distancias, las derivadas del tiempo y los factores de escala están interrelacionados dentro de un sistema de coordenadas mediante dos grupos de vectores base:

vectores de base que son localmente tangentes a su línea de coordenadas asociada: ${displaystyle mathbf {b} ¿Qué? {partial mathbf {r} } {partial q^{i}}}$ son vectores contravariantes (denotados por índices reducidos), y
vectores de base que son localmente normales a la isosurfa creada por las otras coordenadas: ${displaystyle mathbf {b} ^{i}=nabla q^{i}$ son vectores covariantes (denotados por índices elevados), aviso es el operador.

Tenga en cuenta que, debido a la convención de suma de Einstein, la posición de los índices de los vectores es opuesta a la de las coordenadas.

En consecuencia, un sistema de coordenadas curvilíneo general tiene dos conjuntos de vectores base para cada punto: {b₁, b₂, b₃} es la base contravariante, y {b¹, b ², b³} es la base covariante (también conocida como recíproca). Los tipos de vectores de base covariantes y contravariantes tienen direcciones idénticas para los sistemas de coordenadas curvilíneas ortogonales, pero como es habitual tienen unidades invertidas entre sí.

Tenga en cuenta la siguiente igualdad importante:

{displaystyle mathbf {b} }cdot mathbf {b} ¿Qué?

{displaystyle delta _{j}{i}}

Prueba

En el sistema de coordenadas cartesianas ${fnMicrosoft Sans Serif}$ , podemos escribir el producto del punto como:

{displaystyle mathbf {b} ¿Por qué? q_{i}} {dfrac {partial y}{partial {fnMicrosoft Sans Serif}cdot left({dfrac {partial q_{i}right)cdot left({dfrac {partial {fnMicrosoft Sans Serif} q_{j} {partial y}} {dfrac {partial {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {f} {fnMicrosoft Sans Serif} q_{i}{dfrac {partial q_{j}{partial ##### {dfrac {partial y}{partial {fnK} {fnMicroc {fnMicrosoft Sans Serif} {f}} {fnMicroc} {f}} {fn}} {f}}} {fnMicrosoft} {fn}}}} {fnMicroc {f}} {fnMicroc}}}}}}} {f} {f}}}}}} {f}}}}} {b}}}}}}} {b}}}}}}}}} {f} {f}} {dfracdfracdfracf} {f}}}}}}}}}} {f} {f}}}} {f}}}}}}}}}}}}}}}}}}}f} {f} {f} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} Y... q_{i} {dfrac {partial q_{j}{}{partial z}}} {f}

Considerar un desplazamiento infinitesimal ${displaystyle dmathbf} =dxcdot mathbf {e} ¿Por qué? ¿Por qué?$ . Dejadme.₁, dq₂ y dq₃ denota los cambios infinitesimal correspondientes en coordenadas curvilinear q₁q₂ y q₃ respectivamente.

Por la regla de la cadena, dq₁ puede expresarse como:

{displaystyle Dq_{1}={dfrac {partial q_{1}{partial. {cMicrosoft Sans Serif} q_{1}{partial Y... {partial q_{1}{partial z}dz={dfrac {cMicrosoft Sans Serif} q_{1}{partial ##dx+{dfrac {partial q_{1}{partial y}left({dfrac {partial y}{partial q_{1}dq_{1}+{dfrac {partial y}{partial q_{2}dq_{2}+{dfrac {partial y}{partial ¿Qué? {fnMicroc {fnK} {fnK}} {fnMicroc {fn} {f} {f}} {fn}}} {fnMicroc {fn} {fn}} {f}}} {f}}}} {f}}} {f}}}}b}}}}}p}}}}}}}}}}}}p}p}p}p}p}p}p}p}p}p}p}p}p}p}p}p}p}p}p}b}p}pppppp}pb}p}pppppppppp}p}ppp}pp}p}cpp}p}bh}pp} q_{1}dq_{1}+{dfrac {partial z}{partial q_{2}dq_{2}+{dfrac {partial z}{partial ¿Qué?

Si el desplazamiento dr es tal que dq₂ = dq₃ = 0, es decir, el vector de posición r se mueve por una cantidad infinitesimal a lo largo del eje de coordenadas q₂=Contesta y q₃=Consto, entonces:

{displaystyle Dq_{1}={dfrac {partial q_{1}{partial. {partial q_{1}{partial ¿Qué? q_{1}dq_{1}+{dfrac {partial q_{1}{partial {fnMicrosoft} {fnMicrosoft} {fnMicrosoft} {fnMicrosoft}} {f}}} {fnMicrosoft}}} {fnMicrosoft}}}} {fnMicrosoft} {f}}} {f}} {fnMicroc}}} {f}}} {f}f}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {f}}}}}}}}} {f} {f}} {f}}}}f}f}}}f} {f}f}f}f} {f}f}f}f}f}f}f}f}f}f}f}f}f}f}b}f}f}f}f}f}f}f}f}b} q_{1}dq_{1}

Dividiendo por dq₁, y tomar el límite dq₁ → 0:

{displaystyle 1={dfrac {fnMicrosoft {fnMicrosoft Sans Serif} q_{1}{partial # {dfrac {partial x}{partial q_{1}}+{dfrac {partial q_{1}{partial ¿Qué? q_{1}}+{dfrac {partial q_{1}{partial {fnMicrosoft} {fnMicrosoft} {fnMicrosoft} {fnMicrosoft}} {f}}} {fnMicrosoft}}} {fnMicrosoft}}}} {fnMicrosoft} {f}}} {f}} {fnMicroc}}} {f}}} {f}f}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {f}}}}}}}}} {f} {f}} {f}}}}f}f}}}f} {f}f}f}f} {f}f}f}f}f}f}f}f}f}f}f}f}f}f}b}f}f}f}f}f}f}f}f}b} {fnK}}={dfrac {partial x}{partial q_{1} {dfrac {cMicrosoft Sans Serif} q_{1}{partial ##### {dfrac {partial y}{partial {fnMicroc} {fnMicrosoft Sans Serif} q_{1}{partial Y... q_{1} {dfrac {cMicrosoft Sans Serif} q_{1}{partial z}}

o equivalentemente:

{displaystyle mathbf {b} _{1}cdot mathbf {b} ^{1}=1}

Ahora si el desplazamiento dr es tal que dq₁=dq₃=0, es decir, el vector de posición r se mueve por una cantidad infinitesimal a lo largo del eje de coordenadas q₁=Consto y q₃=Consto, entonces:

{displaystyle 0={dfrac {fnMicroial q_{1}{partial. {partial q_{1}{partial ¿Qué? q_{2}dq_{2}+{dfrac {partial q_{1}{partial {fnMicrosoft} {fnMicrosoft} {fnMicrosoft} {fnMicrosoft}} {f}}} {fnMicrosoft}}} {fnMicrosoft}}}} {fnMicrosoft} {f}}} {f}} {fnMicroc}}} {f}}} {f}f}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {f}}}}}}}}} {f} {f}} {f}}}}f}f}}}f} {f}f}f}f} {f}f}f}f}f}f}f}f}f}f}f}f}f}f}b}f}f}f}f}f}f}f}f}b} q_{2}dq_{2}

Dividir por dq₂, y tomar el límite dq₂ → 0:

{displaystyle 0={dfrac {fnMicroial q_{1}{partial # {dfrac {partial x}{partial q_{2}}+{dfrac {partial q_{1}{partial ¿Qué? q_{2}}+{dfrac {partial q_{1}{partial {fnMicrosoft} {fnMicrosoft} {fnMicrosoft} {fnMicrosoft}} {f}}} {fnMicrosoft}}} {fnMicrosoft}}}} {fnMicrosoft} {f}}} {f}} {fnMicroc}}} {f}}} {f}f}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {f}}}}}}}}} {f} {f}} {f}}}}f}f}}}f} {f}f}f}f} {f}f}f}f}f}f}f}f}f}f}f}f}f}f}b}f}f}f}f}f}f}f}f}b} q_{2}={dfrac {partial x}{partial q_{2} {dfrac} {cMicrosoft Sans Serif} q_{1}{partial ##### {dfrac {partial y}{partial {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} q_{1}{partial Y... q_{2} {dfrac} {cMicrosoft Sans Serif} q_{1}{partial z}}

o equivalentemente:

{displaystyle mathbf {b} _{2}cdot mathbf {b} ^{1}=0}

Y así sucesivamente para los otros productos de punto.

Prueba alternativa:

{displaystyle delta _{j}{i}dq^{j}=dq^{i}=nabla q^{i}cdot dmathbf {r} # Mathbf {b} ^{i}cdot {dfrac {partial mathbf {r}{partial ¿Por qué?

y la convención de sumación de Einstein es implícita.

Un vector v se puede especificar en términos de cualquier base, es decir,

{displaystyle mathbf {v} =v^{1}mathbf {b} ¿Qué? ¿Qué? ¿Qué? ¿Qué?

Usando la convención de suma de Einstein, los vectores base se relacionan con los componentes por

{displaystyle mathbf {v} cdot mathbf {b} ¿Qué? ¿Qué?

{displaystyle mathbf {v} cdot mathbf {b} ¿Qué? ¿Por qué? ¿Qué?

{displaystyle mathbf {v} cdot mathbf {b} ¿Por qué? ¿Qué?

{displaystyle mathbf {v} cdot mathbf {b} ¿Qué?

donde g es el tensor métrico (ver más abajo).

Un vector se puede especificar con coordenadas covariantes (índices reducidos, escritos v_k) o coordenadas contravariantes (índices elevados, escritos v^{k}). De las sumas de vectores anteriores, se puede ver que las coordenadas contravariantes están asociadas con vectores de base covariantes, y las coordenadas covariantes están asociadas con vectores de base contravariantes.

Una característica clave de la representación de vectores y tensores en términos de componentes indexados y vectores base es la invariancia en el sentido de que los componentes vectoriales que se transforman de manera covariante (o contravariante) se emparejan con vectores de base que se transforman de manera contravariante (o covariante).

Integración

Construcción de una base covariante en una dimensión

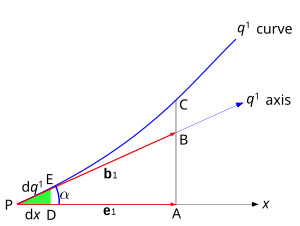
Considere la curva unidimensional mostrada en Fig. 3. Al punto P, tomado como origen, x es una de las coordenadas cartesianas, y q¹ es una de las coordenadas curvilíneas. El vector local de base (no unidad) es b₁ (notado) h₁ arriba, con b reservado para vectores de unidad) y se construye sobre q¹ eje que es un tangente a esa línea de coordenadas en el punto P. El eje q¹ y así el vector b₁ forma un ángulo ${displaystyle alpha }$ con el cartesiano x axis y la base cartesiana vector e₁.

Se puede ver en el triángulo PAB que

{displaystyle cos alpha ={cfrac {fnMitbf} ################################################################################################################################################################################################################################################################ _{1} sobrevivir_mathbf {b}

donde |e₁|, |b₁| son las magnitudes de los dos vectores base, es decir, las intersecciones escalares PB y PA. PA es también la proyección de b₁ en el eje x.

Sin embargo, este método para transformaciones de vectores base usando cosenos direccionales no es aplicable a coordenadas curvilíneas por las siguientes razones:

Aumentando la distancia P, el ángulo entre la línea curvada q¹ y el eje cartesiano x cada vez más se desvía ${displaystyle alpha }$ .
A la distancia PB el verdadero ángulo es el que el tangente en el punto C formas con las x el eje y el último ángulo son claramente diferentes ${displaystyle alpha }$ .

Los ángulos que forman la línea q¹ y ese eje con el eje x se vuelven más cercanos en valor cuanto más nos acercamos al punto P y se vuelven exactamente iguales en P.

Let point E estar situado muy cerca P, tan cerca que la distancia PE es infinitamente pequeño. Entonces... PE medido en el q¹ axis casi coincide con PE medido en el q¹ línea. Al mismo tiempo, la relación PD/PE ()PD ser la proyección de PE sobre x axis) se vuelve casi exactamente igual a ${displaystyle cos alpha }$ .

Dejemos que las intersecciones infinitamente pequeñas PD y PE se etiqueten, respectivamente, como dx y dq<. sup>1. Entonces

{displaystyle cos alpha {fnMicroc}= {fnMicroc} {fnMitbf} ¿Qué? - ¿Por qué?

Por lo tanto, los cosenos direccionales se pueden sustituir en transformaciones con las proporciones más exactas entre intersecciones de coordenadas infinitamente pequeñas. De ello se deduce que la componente (proyección) de b₁ en el eje x es

{displaystyle ¿Por qué? {fnMitbf} ################################################################################################################################################################################################################################################################ _{1}tuvos [b] _{1} {fnMitbf} _{1} sufrimiento {mathbf {e} _{1}}cos alpha = tuberculosismathbf {b} ¿Qué? Rightarrow quad {cfrac {fnK} {fnK} {fnMicrosoft}} {fnMicrosoft} {f}} {f}}} {fnMicrosoft}} {f}}} {fnMicrosoft}}} {f}} {fnMitb} {f}}}} {f}}}} {f}}}}}} {f}}} {f}}}}}}}}}}}}} {f} {f}}}}}}}}}}}}}}}}} {f} {f}} {f}}}}}}}}}}}}}}}}}}}}} {f} {f} {f}}} {f} {f} {f}f}f}f} {f}f}}f}f}f}f}f}f}f}f}f}f}fn ¿Qué?

Si qⁱ = qⁱ()x₁, x₂, x₃) y x_i = x_i()q¹, q², q³) son suaves (continuamente diferenciables) las relaciones de transformación se pueden escribir como ${displaystyle {cfrac {partial} q^{i}{partial #$ y ${displaystyle {cfrac {partial} {fn} {fn}}} {fn}}}} {fn}}}}}}}} {fn}}}} {fn}}}}}}}}}}}}}}}}}}}}}}}} {\\\\fn}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {$ . Es decir, esas ratios son derivados parciales de coordenadas pertenecientes a un sistema con respecto a las coordenadas pertenecientes al otro sistema.

Construyendo una base covariante en tres dimensiones

Haciendo lo mismo para las coordenadas en las otras 2 dimensiones, b₁ se puede expresar como:

{displaystyle mathbf {b} ¿Qué? ¿Qué? ¿Qué? {}={frac {partial x_{1}{partial} {fnMicrosoft Sans Serif} # Mathbf # ################################################################################################################################################################################################################################################################ # Mathbf # ################################################################################################################################################################################################################################################################ # Mathbf # ¿Qué?

Se aplican ecuaciones similares para b₂ y b₃, de modo que la base estándar {e ₁, e₂, e₃} se transforma en una base local (ordenada y normalizada) {b₁, b₂, b₃} mediante el siguiente sistema de ecuaciones:

{displaystyle {begin{aligned}mathbf {b} {{1} {c}={cfrac {partial x_{1}}}{partial}}} { # Mathbf # ################################################################################################################################################################################################################################################################ # Mathbf # ################################################################################################################################################################################################################################################################ Mathbf... ################################################################################################################################################################################################################################################################ {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft}} {cH}} {fnMicrosoft}}} {fnMicrosoft}}}} {fnMicrosoft}}}}} {f}}}} {fnMicrosoft}}}}}}}} { # Mathbf # ################################################################################################################################################################################################################################################################ # Mathbf # ################################################################################################################################################################################################################################################################ Mathbf... ################################################################################################################################################################################################################################################################ # Mathbf # ################################################################################################################################################################################################################################################################ # Mathbf # ###{2}+{cfrac {partial x_{3}{partial - ¿Qué?

Mediante un razonamiento análogo, se puede obtener la transformación inversa de base local a base estándar:

{displaystyle {begin{aligned}mathbf {e} {}{1} {frac {partial q^{1}}{partial}}{ Mathbf ################################################################################################################################################################################################################################################################ Mathbf ################################################################################################################################################################################################################################################################ Mathbf ¿Qué? ################################################################################################################################################################################################################################################################ Mathbf ################################################################################################################################################################################################################################################################ Mathbf ################################################################################################################################################################################################################################################################ Mathbf ¿Qué? ################################################################################################################################################################################################################################################################ Mathbf ################################################################################################################################################################################################################################################################ Mathbf ################################################################################################################################################################################################################################################################ Mathbf ¿Qué?

Jacobiano de la transformación

Los sistemas de ecuaciones lineales anteriores se pueden escribir en forma matricial usando la convención de suma de Einstein como

{displaystyle {cfrac {partial} {fnK} {fnMicrosoft}fnMicrosoft} ¿Por qué? q^{i}{partial Mathbf ¿Qué?

Esta matriz de coeficientes del sistema lineal es la matriz jacobiana (y su inversa) de la transformación. Estas son las ecuaciones que se pueden utilizar para transformar una base cartesiana en una base curvilínea y viceversa.

En tres dimensiones, las formas expandidas de estas matrices son

{displaystyle mathbf {J} ={begin{bmatrix}{cfrac {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft}} {cH}} {fnMicrosoft}}} {fnMicrosoft}}}} {fnMicrosoft}}}}} {f}}}} {fnMicrosoft}}}}}}}} { q^{1}} {cfrac {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft}} {cH}} {fnMicrosoft}}} {fnMicrosoft}}}} {fnMicrosoft}}}}} {f}}}} {fnMicrosoft}}}}}}}} { q^{2}} {cfrac {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft}} {cH}} {fnMicrosoft}}} {fnMicrosoft}}}} {fnMicrosoft}}}}} {f}}}} {fnMicrosoft}}}}}}}} { q^{3}\ {fnK} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}} {f}} {fnMicrosoft}} {fnMicrosoft}}}}} {fnMicrosoft}} {fnMicrosoft}}} {fnMicrosoft}}}}} {f}}}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} { q^{1}} {cfrac {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}} {f}} {fnMicrosoft}} {fnMicrosoft}}}}} {fnMicrosoft}} {fnMicrosoft}}} {fnMicrosoft}}}}} {f}}}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} { q^{2}} {cfrac {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}} {f}} {fnMicrosoft}} {fnMicrosoft}}}}} {fnMicrosoft}} {fnMicrosoft}}} {fnMicrosoft}}}}} {f}}}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} { q^{3}\ {fnK} {fnK} {fn}} {c}}}} {cH00}}} {c}} {c}}} {c}}}} {c}}}} {c}}}}}}} {c}}}} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}} {f}} {fnMicrosoft}}} {fnMicrosoft}}}}} {fnMicrosoft}}}} {f}}}}} {fnMicrosoft}}}}}}}}}} { q^{2}} {cfrac {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}} {f}} {fnMicrosoft}}} {fnMicrosoft}}}}} {fnMicrosoft}}}} {f}}}}} {fnMicrosoft}}}}}}}}}} { q^{3}\end{bmatrix}quad mathbf {J} ^{-1}={begin{bmatrix}{cfrac {partial q^{1}{partial x_{1}} {cfrac {partial q^{1}{partial x_{2}} {cfrac {partial q^{1}{partial {fnK}}\\frac {fnMicrosoft Sans Serif} {fnK}} {fnMicrosoft}} {fn}} {fnK}}} {fnK}}}}}\\\\\\\\\cH\\cH3}}}}}}\\\\\\\\\\\\\\\\\cH\\\\cHcH\\\\cHcH\\\\\\\\cHcH3\\cH\\\cH\\cH\\\\cH3\\cH3cHcH\\\cH\\cH3\\\cH x_{1}} {cfrac {partial q^{2}{partial x_{2}} {cfrac {partial q^{2}{partial {fnK}\\fnK} {fnK}} {fnMicrosoft}} {fnK}} {f}}}}\\\cH0}} {\cH0}}}}\\\\\\\\cH00}}\\\\\\\cH\\cH3\\cH3cH3cH3cH3\cH3cH3\\cH00cH3\\\\cH\\\\\\\\\cHcH3\\cH3\\cH\\\\\\\cH3\cH3}}}}}}}\\\\\\\\\\\cH x_{1}} {cfrac {partial q^{3}{partial x_{2}} {cfrac {partial q^{3}{partial ¿Qué?

En la transformación inversa (segundo sistema de ecuaciones), las incógnitas son los vectores de base curvilínea. Para cualquier ubicación específica solo puede existir uno y solo un conjunto de vectores base (de lo contrario, la base no está bien definida en ese punto). Esta condición se cumple si y sólo si el sistema de ecuaciones tiene una única solución. En álgebra lineal, un sistema de ecuaciones lineales tiene una solución única (no trivial) solo si el determinante de la matriz de su sistema es distinto de cero:

{displaystyle det(mathbf {J} ^{-1})neq 0}

que muestra el fundamento del requisito anterior relativo al determinante jacobiano inverso.

Generalización a n dimensiones

El formalismo se extiende a cualquier dimensión finita de la siguiente manera.

Considere el espacio euclidiano n-dimensional real, es decir, Rⁿ = R × R ×... × R (n veces) donde R es el conjunto de valores reales números y × denota el producto cartesiano, que es un espacio vectorial.

Las coordenadas de este espacio se pueden denotar por: x = (x₁, x₂,...,x_n). Como se trata de un vector (un elemento del espacio vectorial), se puede escribir como:

{displaystyle mathbf {x} = ¿Qué?

donde e¹ = (1,0,0...,0), e² = (0,1,0...,0), e³ = (0,0,1...,0),...,eⁿ = (0,0,0...,1) es el conjunto básico estándar de vectores para el espacio Rⁿ, y i = 1, 2,...n Es un índice que etiqueta los componentes. Cada vector tiene exactamente un componente en cada dimensión (o "eje") y son mutuamente ortogonales (perpendiculares) y normalizados (tienen magnitud unitaria).

De manera más general, podemos definir los vectores base b_i de modo que dependan de q = (q₁, q₂,...,q_n), es decir, cambian de un punto a otro: b_i = b_i(q). En cuyo caso definir el mismo punto x en términos de esta base alternativa: las coordenadas con respecto a esta base v_i también depende necesariamente de x, es decir, v_i = v_i(x). Entonces, un vector v en este espacio, con respecto a estas coordenadas alternativas y vectores base, se puede expandir como una combinación lineal en esta base (lo que simplemente significa multiplicar cada vector base e_i por un número v_i – multiplicación escalar):

{fn} {fn} {fn} {fn} {fn}m}m}mthbf {} {c}=cH} {f}} {c} {f} {f}} {f} {f} {f} {f}}f}}f}f}f}f}f} {f}f} {f}}f}}}}f}}}f}f}}f}f}f}}f}f}f}f}}f}f}f}}f}}f}f}f}f}f} {f}f}}}}}}}}f}f} {f}}f}f}f}}f}}}}}}}f}f}}}}}}f}}}f}}}}}}}}}}

La suma vectorial que describe v en la nueva base se compone de diferentes vectores, aunque la suma en sí sigue siendo la misma.

Transformación de coordenadas

Desde una perspectiva más general y abstracta, un sistema de coordenadas curvilíneo es simplemente un parche de coordenadas en la variedad diferenciable Eⁿ (espacio euclidiano de n dimensiones) que es difeomorfa. al parche de coordenadas cartesianas en el colector. No es necesario que dos parches de coordenadas difeomorfas en una variedad diferencial se superpongan de manera diferenciable. Con esta definición simple de un sistema de coordenadas curvilíneo, todos los resultados que siguen a continuación son simplemente aplicaciones de teoremas estándar en topología diferencial.

Las funciones de transformación son tales que existe una relación uno a uno entre los puntos de la "antigua" y "nuevo" coordenadas, es decir, esas funciones son biyecciones y cumplen los siguientes requisitos dentro de sus dominios:

Son funciones suaves: qⁱ = qⁱ()x)
El determinante inverso Jacobiano
${displaystyle J^{-1}={begin{vmatrix}{dfrac {partial q^{1}{partial ################################################################################################################################################################################################################################################################ {partial q^{1}{partial #### {2} {cdots > {dfrac {partial q^{1}{partial ¿Qué? {partial q^{2}{partial ################################################################################################################################################################################################################################################################ {partial q^{2}{partial #### {2} {cdots > {dfrac {partial q^{2}{partial x_{n}}\\vdots >vdots >vdots \{dfrac {partial q^{n}{partial {fn}} {dfrac {fn} {fn} {fn}}} {fn}}}}} {dfrac {fn}}} {fn}}}} {fn}}}}}}}} {dfrac {dfrac {ccH00}}}}}}}}}} { {fn}} {cdots}{dfrac {partial q^{n}{partial #### {n}end{vmatrix}neq 0}$
no es cero; significa que la transformación es invertible: x_i()q).
según el teorema de función inversa. La condición de que el determinante jacobino no es cero refleja el hecho de que tres superficies de diferentes familias se intersectan en un solo punto y así determinar la posición de este punto de una manera única.

Álgebra vectorial y tensorial en coordenadas curvilíneas tridimensionales

El álgebra elemental de vectores y tensores en coordenadas curvilíneas se utiliza en parte de la literatura científica más antigua sobre mecánica y física y puede ser indispensable para comprender trabajos de principios y mediados del siglo XX, por ejemplo, el texto de Green y Zerna. En esta sección se dan algunas relaciones útiles en el álgebra de vectores y tensores de segundo orden en coordenadas curvilíneas. La notación y el contenido son principalmente de Ogden, Naghdi, Simmonds, Green y Zerna, Basar y Weichert y Ciarlet.

Tensores en coordenadas curvilíneas

Un tensor de segundo orden se puede expresar como

{displaystyle {boldsymbol {S}=S^{ij}mathbf {b} _{i}otimes mathbf {b} ¿Qué? {b} _{i}otimes mathbf {b} ^{j}=S_{i}{j}mathbf {b} {i}otimes mathbf {b} ¿Por qué?

Donde ${displaystyle scriptstyle otimes }$ denota el producto tensor. Los componentes S^ij son llamados contravariante componentes, Sⁱ _j el mixto derecho-covariante componentes, S_i ^j el mixto izquierda-covariante componentes y S_ij el covariante componentes del tensor de segundo orden. Los componentes del tensor de segundo orden están relacionados por

{displaystyle S^{jk}=g^{k} {} {j}=g}S^{i}{i}=g} {k}=g^{k} {jf}G}{jf} }S_{kell }

El tensor métrico en coordenadas curvilíneas ortogonales

En cada punto, se puede construir un pequeño elemento de línea $d x$ , por lo que el cuadrado de la longitud del elemento de línea es el producto escalar dx • dx y se llama métrica del espacio, dada por:

{displaystyle dmathbf {x} cdot dmathbf {x} ={cfrac {cMicrosoft Sans Serif} x_{i}{partial {fnK} {cHFF} {cHFF}} {cHFF}} {c}}} {cH}} {c}} {cH}}}} {cH}}} {c}}}}} {c}}}} {cH}}} {crrac {cH}}} {c}}}} {cH}}}}} {cH}}}}} {cH}}}}} {cr}}}} {c}}}}}}}}}}} {c} {c} {c}}}}}} {c}}}}}}}}} {cH}} {c}}} {cH}} {c}}}}} {ccccc}}} {c} {cH}}} {c}}}}}}}}}}}}}}}}}}}} {c}} ¿Qué?

La siguiente parte de la ecuación anterior

{displaystyle {cfrac {partial} x_{k}{partial {cHFF} {cHFF} {cHFF}} {cHFF}} {cHFF}} {cH00}}} {cH}} {c}}} {cH}}}}}} {c}} {cH}}}} {cH}}}} {cH00}}}}} {c}}}} {cH}}}}}}}}}}}} {cr}}} {cr}}} {c}}} {c}}} {c}}} {c}}}}}} {c}}}}}}} {c}}}}} {cc}}}}}} {c}}}} {c}}}}} {ccccccc} {c}}} {c}} {c}}}} {cH}}}}} {c}} {c}}} ¿Qué?

es un tensor simétrico llamado tensor fundamental (o métrico) del espacio euclidiano en coordenadas curvilíneas.

Los índices pueden subir y bajar según la métrica:

{displaystyle v^{i}=g^{ik}v_{k}

Relación con los coeficientes de Lamé

Definición de los factores de escala h_i por

{displaystyle ¿Qué? {b}cdot mathbf {b} ##{j}quad Rightarrow quad ¿Por qué? {partial mathbf {x} {fnMicrosoft Sans Serif}

da una relación entre el tensor métrico y los coeficientes de Lamé, y

{displaystyle g_{ij}={cfrac {partial mathbf {x} } {cdot {cf {racpartial mathbf {x} {cdot {cdot} {cdot {cH00} {cdot {cH00} {cH00} {cH00}} {cdot {cdot {cH00} {cH00} {cH00}}}} {cdot} {cdot {cdot {cdot {cdot {cdot {cH00} {cH00} {cdot {c} {cH00}} {c}}}}}}}} {cdot {c} {cdot {cdot {c} {cdot {c}}} {cdot {cdot {c} {c} {cdot {c} {c} {c} {c} {cdot {c}} {c ¿Por qué?

donde h_ij son los coeficientes de Lamé. Para una base ortogonal también tenemos:

{displaystyle g=g_{11}g_{22}g_{33}=h_{1}h_{2}h_{2}h_{3} {2}quad Rightarrow quad {sqrt {g}=h_{1}h_{2}h_{3}=J}

Ejemplo: coordenadas polares

Si consideramos las coordenadas polares de R²,

{displaystyle (x,y)=(rcos thetarsin theta)}

(r, θ) son las coordenadas curvilíneas y el determinante jacobiano de la transformación (r,θ) → (r cos θ, r sen θ) es r.

Los vectores de base ortogonales son b_r = (cos θ, sin θ), b_θ = (−r sen θ, r cos θ). Los factores de escala son h_r = 1 y h_θ= r. El tensor fundamental es g₁₁ =1, g₂₂ =r², g₁₂ = g₂₁ =0.

El tensor alterno

En una base ortonormal para diestros, el tensor alterno de tercer orden se define como

{displaystyle {boldsymbol {Mathcal {E}= 'varepsilon ¿Por qué?

En una base curvilínea general, el mismo tensor se puede expresar como

{displaystyle {boldsymbol {Mathcal {E}}={s}_{ijk}mathbf {b}otimes mathbf {b} ^{j}otimes mathbf {b} ^{k}={mathcal {E} {\fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}

También se puede demostrar que

{displaystyle {fnMithcal} {fnK} {fnMicrosoft} {fnMicrosoft} {f}} {fnK}}} {fnMicrosoft}} {fnMicrosoft} {fn}}}}} {f}f}}}fnKfnK}}}}f}f}f}f}f} {1}{J}varepsilon ¿Qué? Varepsilon ¿Qué?

Símbolos de Christoffel

Christoffel símbolos del primer tipo ${displaystyle "Gamma"$

{displaystyle mathbf {b} ¿Por qué? {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} - ¿Qué? Gamma _{kij}quad Rightarrow quad mathbf {b} _{k}cdot mathbf {b} _{i, J}=Gamma _{kij}

donde la coma denota una derivada parcial (ver cálculo de Ricci). Para expresar Γ_kij en términos de g_ij,

{displaystyle {begin{aligned}g_{ij,k} limit=(mathbf {b} ¿Qué? ¿Por qué? ¿Por qué? - ¿Qué? Gamma _{jik}+ Gamma ################################################################################################################################################################################################################################################################ ¿Qué? ¿Qué? ¿Por qué? _{k,j}= Gamma _{kij}+ Gamma ################################################################################################################################################################################################################################################################ ¿Por qué? ¿Qué? _{k,i}= Gamma _{kji}+Gamma ¿Qué?

Desde

{displaystyle mathbf {b} ¿Por qué? Rightarrow quad Gamma _{kij}=Gamma _{kji}}

usarlos para reorganizar las relaciones anteriores proporciona

{displaystyle Gamma _{kij}={frac {1}{2} {g_{ik,j}+g_{jk,i}-g_{ij,k}={frac {1}{2}}[(mathbf {b} _{i}cdot mathbf {b})_{,j}+(mathbf {b} Yo... ¿Qué? ¿Qué?

Christoffel símbolos del segundo tipo ${displaystyle "Gamma"$

{displaystyle "Gamma" Gamma ¿Qué? {cfrac {partial mathbf {b} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} ¿Por qué? Gamma.

Esto implica que

{displaystyle Gamma ¿Qué? {partial mathbf {b} {fnK}cdot mathbf {b}=-mathbf {b} _{i}cdot {cdot {crrac {partial mathbf {b} {} {c} {c} {c} {c} {c}} {c} {c} {c}}}} {c}}} {c}}}} {c}} {c}}}} {c}}}}}} {c} {cdot}}}}}}}}} {c} {cdotc}c}}}}}}} {c} {c} {c} {cdot} {c} {cdot} {c} {cdotcdotcdot {c} {c} {cdot {cdot {c}c}c}c}c} {c} {c} q^{j}}quad }

desde entonces

{displaystyle quad {cfrac {partial }{partial q^{j}}(mathbf {b} ¿Qué?

Otras relaciones que siguen son

{displaystyle {cfrac {partial mathbf {b} ^{i}{partial q^{j}=- Gamma. {b} ^{k},quad {boldsymbol {nabla}mathbf {b} ¿Qué? Gamma. {b} _{k}otimes mathbf {b} ^{j},quad {boldsymbol {nabla}mathbf {b} ^{i}=- Gamma. {b} {k}otimes mathbf {b} {j}

Operaciones vectoriales

Producto de puntos:
El producto escalar de dos vectores en coordenadas curvilinear es
${displaystyle mathbf {u} cdot mathbf {v} =u^{i}v_{i}=u_{i}=g_{i}u}{i}v}=g}{i} {j}=g}{i}u_{i}u_}u_} {} {} {}}} {} {} {}}}} {} {} {} {}} {}}}}}} {}} {} {} {}}}} {}}} {} {} {} {} {}} {} {}}}}}}}} {}}}}}} {} {} {}}}}}} {}}}}} {} {} {} {} {}}} {}}}}}} {}}}}}} {} {}}}}}}}}}} {}}}}}}}}}}} {}}}}}}}}}}}} {} {} {}}}}}}}}}}}$
Producto cruzado:
El producto cruzado de dos vectores es dado por
${displaystyle mathbf {u} times mathbf {v} ¿Qué? {fnK}$
Donde ${displaystyle epsilon _{ijk}}$ es el símbolo de permutación y ${displaystyle mathbf {e} _{i}$ es un vector de base cartesiana. En coordenadas curvilinear, la expresión equivalente es
${displaystyle mathbf {u} times mathbf {v} =[mathbf {b} ¿Por qué? {fn} {fn} {fn}} {fn}}} {fn}} {fn} {fn}} {fn}}} {fn}}}}}} {fn}}}}}}}}}} {\fn}}}}}}}}}\\\fn}fn}}}}}}}}}}}}\\\\\\\\\\\\\\\\\fn}}}}}\\\\\\\\\\\\\\\\\\\\\\\\\\\fn}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$
Donde ${displaystyle {fnMithcal {}_{ijk}}$ es el tensor alternado de tercera orden.

Cálculo vectorial y tensorial en coordenadas curvilíneas tridimensionales

Es necesario realizar ajustes en el cálculo de integrales de línea, superficie y volumen. Para simplificar, lo siguiente se limita a tres dimensiones y coordenadas curvilíneas ortogonales. Sin embargo, los mismos argumentos se aplican a espacios n-dimensionales. Cuando el sistema de coordenadas no es ortogonal, hay algunos términos adicionales en las expresiones.

Simmonds, en su libro sobre análisis de tensores, cita a Albert Einstein diciendo

La magia de esta teoría apenas fallará en imponerse a cualquiera que realmente la haya comprendido; representa un verdadero triunfo del método del cálculo diferencial absoluto, fundado por Gauss, Riemann, Ricci y Levi-Civita.

El cálculo vectorial y tensorial en coordenadas curvilíneas generales se utiliza en el análisis tensorial en variedades curvilíneas de cuatro dimensiones en la relatividad general, en la mecánica de capas curvas y en el examen de las propiedades de invariancia de las ecuaciones de Maxwell, que han sido de interés. en metamateriales y en muchos otros campos.

En esta sección se dan algunas relaciones útiles en el cálculo de vectores y tensores de segundo orden en coordenadas curvilíneas. La notación y el contenido son principalmente de Ogden, Simmonds, Green y Zerna, Basar y Weichert y Ciarlet.

Sea φ = φ(x) un campo escalar bien definido y v = v(x) un campo vectorial bien definido, y λ₁, λ₂... ser parámetros de las coordenadas

Elementos geométricos

vector tangente: Si x()λ) parametriza una curva C en coordenadas cartesianas, entonces
${displaystyle {partial mathbf {x} over partial lambda }={partial mathbf {x} over partial q^{i}{partial q^{i} over partial lambda #=left(h_{ki}{cfrac {fnMicrosoft Sans Serif}nMitbf {b} ¿Qué?$
es un vector tangente C en coordenadas curvilinear (utilizando la regla de la cadena). Usando la definición de los coeficientes de Lamé, y eso para la métrica g_ij = 0 cuando i ل j, la magnitud es:
${displaystyle lefttención{partial mathbf {x} over partial lambda "Justo en la vida" {h_{ki}h_{kj}{cfrac {partial q^{i}{partial lambda }{cfrac {partial q^{j}{partial lambda {fnK} {fnK}} {fnK} {cHFF}} {fnK}}}} {fn}}} {fn} {f}}}}}}} {fn}}}}}}} {f}}}} {f}}}}} {fnfncfnfnf}}}}}}}} {f}}}}} {\fnf}}}}}} {f}}}}}}}}}}} {\\\\fn\\fnfn\\fn\fnfnfnccccccccccccccccccccccccccccccccccccc {partial q^{i}{partial lambda }{cfrac {partial q^{j}{partial lambda }}={sqrt {h_{i}{2}left({cfrac {partial q^{i}{partial lambda}}}right)}}}}}}}}}} {ccc}}}}}}}} {c}}}}}}}}} {cccccccccc}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {cccccccccccccccccccccccccccccccc}}}}}}}}}}}}}}}}}}}}}}$
Elemento plano tangente: Si x()λ₁, λ₂) parametriza una superficie S en coordenadas cartesianas, entonces el siguiente producto cruzado de vectores tangentes es un vector normal a S con la magnitud del elemento plano infinitesimal, en coordenadas curvilinear. Utilizando el resultado anterior,
${fnMicrosoft Sans Serif} {f} {fnMicrosoft Sans Serif} {f} {f} {f} {f}f} {cHFF}cH00}cH00}b} {cH00}cH00}b} {cH00}cH00}b}b}b}cH00}b}b}cH00}b}cH00}cH00}cH00}cH00}cH00}cH00}b}cH00}cH00}cH00}cH00}cH00}cH00}cH00}cH00}b}b}cH00}b}cH00}cH00}}cH00}cH00}b}b}b}cH00}b}cH00}b}b} ¿Qué? q^{i} over partial lambda ¿Qué? q^{j} over partial lambda ¿Por qué? ¿Qué?$
Donde ${displaystyle {fnMithcal}}$ es el símbolo de permutación. En forma determinante:
${displaystyle {partial mathbf {x} over partial lambda _{1}times {partial mathbf {x} over partial lambda - ¿Por qué? ¿Qué? {partial q^{i}{partial lambda ################################################################################################################################################################################################################################################################ {partial q^{i}{partial lambda ################################################################################################################################################################################################################################################################ {partial q^{i}{partial lambda ¿Qué? h_{1j}{dfrac {partial q^{j}{partial lambda ### {2}} {2j}{dfrac {partial q^{j}{partial lambda {fnMicrosoft Sans Serif} {partial q^{j}{partial lambda ¿Qué?$

Integración

Operador	Scalar field	Vector field
Línea integral	${displaystyle int _{C}varphi (mathbf {x})ds=int _{a}^{b}varphi (mathbf {x} (lambda))left{partial mathbf {x} over partial lambda } 'justo en la vida 'lambda }$	${displaystyle int _{C}mathbf {v} (mathbf {x})cdot dmathbf {s} =int _{a} {b}mathbf {v} (mathbf {x} (lambda))cdot left({partial mathbf {x}$
Superficie integral	${displaystyle int _{S}varphi (mathbf {x})dS=iint _{T}varphi (mathbf {x} (lambda _{1},lambda _{2})left sometida{partial mathbf {x} over partial lambda _{1}f] ¿Por qué? _{1}dlambda ¿Qué?$	${fnMicrosoft Sans Serif} {fnMicrosoft {x}cdot dS=iint _{T}mathbf {v} (mathbf {x} (lambda _{1},lambda _{2})cdot left({partialmathbfx {2} ¿Por qué? _{1}dlambda ¿Qué?$
Volumen integral	${displaystyle iiint _{V}varphi (x,y,z)dV=iiint Jdq_{2}dq_{3}$	${displaystyle iiint _{V}mathbf {u} (x,y,z)dV=iiint _{V}mathbf {v} (q_{1},q_{2},q_{3})Jdq_{1}dq_{2}dq_{3}}$

Diferenciación

Las expresiones para el gradiente, la divergencia y el laplaciano se pueden extender directamente a dimensiones n; sin embargo, la curvatura solo se define en 3D.

El campo vectorial b_i es tangente a la coordenada qⁱ curva y forma una base natural en cada punto de la curva. Esta base, como se analizó al principio de este artículo, también se denomina base curvilínea covariante. También podemos definir una base recíproca, o una base curvilínea contravariante, bⁱ. Todas las relaciones algebraicas entre los vectores de base, como se analiza en la sección sobre álgebra tensorial, se aplican a la base natural y su recíproco en cada punto x.

Operador	Scalar field	Vector field	2a orden campo tensor
Gradiente	${displaystyle nabla varphi ={cfrac {0} {fn} {fnK}} {fn}}} {fn}}} {fn}}}} {f}}}} {fn}}} {fn}}}}} {f}}}}}}}} {f}}}}}} {f}}}}}}} {}}}}} { varphi over partial q^{i}mathbf {b} ^{i}$	${displaystyle nabla mathbf {v} ={cfrac {1}{i} {} {f}} {f}} {f}} {f}}} {f}}}}}} {f}}}}} {f}}}} {f}}}}} {f}}}}} {}}}}}}} { mathbf {v} over partial q^{i}otimes mathbf {b} _{i}$	${displaystyle {boldsymbol {nabla }{boldsymbol {S}={cfrac {partial {boldsymbol {S} {fn} {fnMicrosoft}} {fnMicrosoft}}} {fnMicrosoft}}} {f}}}} {fn}}} {fnMicrosoft}}}}} {fn}}}} {fnMicrosoft}}}}}}}}}}}} { q^{i}otimes mathbf {b}$
Divergence	N/A	${displaystyle nabla cdot mathbf {v} ={cfrac {1}{prod {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}$	${cdot {cdot {cdot {cdot {cdot}cdot mathbf {a} ={boldsymbol {nabla}cdot ({boldsymbol {S}cdot mathbf {a}}$ Donde a es un vector constante arbitrario. En coordenadas curvilinear, ${displaystyle {boldsymbol {nabla}cdot {boldsymbol {}=left {cH00} {cH00} {cHFF} {cH}} {cH}} {cH}} {cH}} {cHFF}}}}}} {cH}} {cH}}} {cH00}}}}}}cH}}}}}}}}}}} { - ¿Qué? Gamma... Gamma ¿Por qué?$
Laplacian	${displaystyle nabla ^{2}varphi ={cfrac {1}{prod {fnMicrosoft Sans Serif} {partial }{}}left({cfrac {prod {fnK} {fnK} {fnK}} {fnMicroc} {partial varphi } {partial q^{i}}right)}$
Curl	N/A	Para campos vectoriales en 3D solamente, ${displaystyle nabla times mathbf {v} ={frac {1} {fn} {fn} {fnK}} {f}}} {\fn}} {\fn}} {fn}}} {fn}}}} {fn}}}} {fn}}}} {f}}} {f}}}}}} {f}}}}}}}}}} {\\\\\\\\\\\fn}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {\ {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}$ Donde ${displaystyle epsilon _{ijk}}$ es el símbolo Levi-Civita.	Ver Curl de un campo de tensor

Fuerzas ficticias en coordenadas curvilíneas generales

Por definición, si una partícula sobre la que no actúan fuerzas tiene su posición expresada en un sistema de coordenadas inercial, (x₁, x₂, x₃, t), entonces allí no tendrá aceleración (d²x_j/dt² = 0). En este contexto, un sistema de coordenadas puede no ser "inercial" ya sea debido a ejes de tiempo no rectos o ejes espaciales no rectos (o ambos). En otras palabras, los vectores base de las coordenadas pueden variar en el tiempo en posiciones fijas, o pueden variar con la posición en momentos fijos, o ambas. Cuando las ecuaciones de movimiento se expresan en términos de cualquier sistema de coordenadas no inercial (en este sentido), aparecen términos adicionales, llamados símbolos de Christoffel. Estrictamente hablando, estos términos representan componentes de la aceleración absoluta (en la mecánica clásica), pero también podemos optar por seguir considerando d²x_j./dt² como la aceleración (como si las coordenadas fueran inerciales) y trate los términos adicionales como si fueran fuerzas, en las que caso se les llama fuerzas ficticias. La componente de cualquier fuerza ficticia normal a la trayectoria de la partícula y en el plano de curvatura de la trayectoria se denomina fuerza centrífuga.

Este contexto más general deja clara la correspondencia entre los conceptos de fuerza centrífuga en sistemas de coordenadas giratorios y en sistemas de coordenadas curvilíneos estacionarios. (Ambos conceptos aparecen con frecuencia en la literatura). Para un ejemplo simple, considere una partícula de masa m que se mueve en un círculo de radio r con velocidad angular . w relativo a un sistema de coordenadas polares que gira con velocidad angular W. La ecuación radial del movimiento es mr” = F_r + mr(w + W)². Por lo tanto, la fuerza centrífuga es mr multiplicada por el cuadrado de la velocidad de rotación absoluta A = w + W de la partícula.. Si elegimos un sistema de coordenadas que gira a la velocidad de la partícula, entonces W = A y w = 0, en cuyo caso la fuerza centrífuga es mrA², mientras que si elegimos un sistema de coordenadas estacionario tenemos W = 0 y w = A, en cuyo caso la fuerza centrífuga vuelve a ser mrA². La razón de esta igualdad de resultados es que en ambos casos los vectores base en la ubicación de la partícula cambian en el tiempo exactamente de la misma manera. Por lo tanto, estas son en realidad dos formas diferentes de describir exactamente la misma cosa, una descripción en términos de coordenadas giratorias y la otra en términos de coordenadas curvilíneas estacionarias, las cuales son no inerciales según el significado más abstracto de ese término..

Al describir el movimiento general, las fuerzas reales que actúan sobre una partícula a menudo se refieren al círculo osculador instantáneo tangente a la trayectoria del movimiento, y este círculo en el caso general no está centrado en una ubicación fija, por lo que la descomposición en Los componentes centrífugos y Coriolis cambian constantemente. Esto es cierto independientemente de si el movimiento se describe en términos de coordenadas estacionarias o giratorias.

Contenido relacionado

Más resultados...