Continuación analítica

En el análisis complejo, una rama de las matemáticas, la continuación analítica es una técnica para extender el dominio de definición de una función analítica determinada. La continuación analítica a menudo logra definir valores adicionales de una función, por ejemplo, en una nueva región donde una representación de serie infinita en términos de la cual se definió inicialmente se vuelve divergente.

Sin embargo, la técnica de continuación paso a paso puede encontrar dificultades. Estos pueden tener una naturaleza esencialmente topológica, dando lugar a inconsistencias (definiendo más de un valor). Alternativamente, pueden tener que ver con la presencia de singularidades. El caso de varias variables complejas es bastante diferente, ya que las singularidades no necesitan ser puntos aislados, y su investigación fue una de las principales razones para el desarrollo de la cohomología de haces.

Discusión inicial

Continuación analítica del logaritmo natural (parte imaginaria)

Suppose f es una función analítica definida en un subconjunto abierto no vacío U del plano complejo ${displaystyle mathbb {C}$. Si V es un subconjunto abierto más grande ${displaystyle mathbb {C}$, que contiene U, y F es una función analítica definida en V tales que

${displaystyle F(z)=f(z)qquad forall zin U,}$

entonces F se llama una continuación analítica de f. En otras palabras, la restricción de F a U es la función f con la que comenzamos.

Las continuaciones analíticas son únicas en el siguiente sentido: si V es el dominio conexo de dos funciones analíticas F₁ y F ₂ tal que U está contenido en V y para todo z en U

${displaystyle F_{1}(z)=F_{2}(z)=f(z),}$

entonces

${displaystyle F_{1}=F_{2}$

en todo V. Esto se debe a que F₁ − F₂ es una función analítica que desaparece en el dominio abierto y conectado U de f y por lo tanto debe desaparecer en todo su dominio. Esto se sigue directamente del teorema de identidad para funciones holomorfas.

Aplicaciones

Una forma común de definir funciones en el análisis complejo consiste en especificar primero la función en un dominio pequeño solamente y luego extenderla mediante la continuación analítica.

En la práctica, esta continuación a menudo se realiza estableciendo primero una ecuación funcional en el dominio pequeño y luego usando esta ecuación para extender el dominio. Algunos ejemplos son la función zeta de Riemann y la función gamma.

El concepto de cobertura universal se desarrolló por primera vez para definir un dominio natural para la continuación analítica de una función analítica. La idea de encontrar la continuación analítica máxima de una función condujo a su vez al desarrollo de la idea de las superficies de Riemann.

La continuación analítica se utiliza en variedades de Riemann, soluciones de las ecuaciones de Einstein. Por ejemplo, la continuación analítica de las coordenadas de Schwarzschild en las coordenadas de Kruskal-Szekeres.

Ejemplo resuelto

Continuación analítica de U (centrado en 1) a V (centrado en a=(3+i)/2)

Comience con una función analítica particular ${displaystyle f}$. En este caso, es dado por una serie de energía centrada en ${displaystyle z=1}$:

${displaystyle f(z)=sum _{k=0}{infty }(-1)^{k}(z-1)^{k}$

Por el teorema Cauchy-Hadamard, su radio de convergencia es 1. Eso es, ${displaystyle f}$ está definido y analítico en el conjunto abierto ${displaystyle U={ Sobrevivenciaz-1$ que tiene límites ${displaystyle partial U={Principio1 subsisten=1}$. De hecho, la serie se divierte en ${displaystyle z=0in partial U}$.

Finge que no sabemos que ${displaystyle f(z)=1/z}$, y centrarse en la actualización de la serie de energía en un punto diferente ${displaystyle ain U}$:

${displaystyle f(z)=sum _{k=0}{infty - Sí.$

Calcularemos el ${displaystyle A_{k}$'s y determinar si esta nueva serie de energía converge en un conjunto abierto ${displaystyle V}$ que no figura en ${displaystyle U}$. De ser así, habremos continuado analíticamente ${displaystyle f}$ a la región ${displaystyle Ucup V}$ que es estrictamente mayor que ${displaystyle U}$.

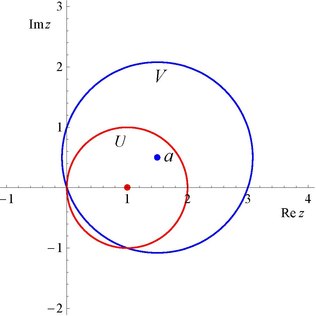
La distancia desde ${displaystyle a}$ a ${displaystyle partial U}$ es ${displaystyle rho =1-resistentesa-1$. Toma. ${displaystyle 0 realizadasrho }$; ${displaystyle D}$ ser el disco de radio ${displaystyle r}$ alrededor ${displaystyle a}$; y ${displaystyle partial D}$ ser su límite. Entonces... ${displaystyle Dcup partial Dsubset U}$. Usando la fórmula de diferenciación de Cauchy para calcular los nuevos coeficientes,

${displaystyle {begin{aligned}a_{k}&={frac {f^{(k)}(a)}{k!}}\&={frac {1}{2pi i}}int _{partial D}{frac {f(zeta)dzeta }{(zeta -a)^{k+1}}}\&={frac {1}{2pi i}}int _{partial D}{frac {sum _{n=0}^{infty }(-1)^{n}(zeta -1)^{n}dzeta }{(zeta -a)^{k+1}}}\&={frac {1}{2pi i}}sum _{n=0}^{infty }(-1)^{n}int _{partial D}{frac {(zeta -1)^{n}dzeta }{(zeta -a)^{k+1}}}\&={frac {1}{2pi i}}sum _{n=0}^{infty }(-1)^{n}int _{0}^{2pi }{frac {(a+re^{itheta }-1)^{n}rie^{itheta }dtheta }{(re^{itheta })^{k+1}}}\&={frac {1}{2pi }}sum _{n=0}^{infty }(-1)^{n}int _{0}^{2pi }{frac {(a-1+re^{itheta })^{n}dtheta }{(re^{itheta })^{k}}}\&={frac {1}{2pi }}sum _{n=0}^{infty }(-1)^{n}int _{0}^{2pi }{frac {sum _{m=0}^{n}{binom {n}{m}}(a-1)^{n-m}(re^{itheta })^{m}dtheta }{(re^{itheta })^{k}}}\&={frac {1}{2pi }}sum _{n=0}^{infty }(-1)^{n}int _{0}^{2pi }{binom {n}{k}}(a-1)^{n-k}dtheta \&=sum _{n=0}^{infty }(-1)^{n}{binom {n}{k}}(a-1)^{n-k}\&=(-1)^{k}a^{-k-1}end{aligned}}}$

Es decir,

${displaystyle f(z)=sum ¿Qué? }a_{k}(z-a)^{k}=sum ¿Por qué? {1}{a}sum ¿Qué?$

que tiene radio de convergencia ${displaystyle Silencioso$, y ${displaystyle V={ habitz-a impercepta sometida}.$ Si elegimos ${displaystyle ain U}$ con ${displaystyle ←$, entonces ${displaystyle V}$ no es un subconjunto de ${displaystyle U}$ y en realidad es más grande en el área que ${displaystyle U}$. La trama muestra el resultado para ${displaystyle a={tfrac {2} {3+i). }$

Podemos continuar el proceso: seleccione ${displaystyle bin Ucup V}$, más reciente la serie de energía ${displaystyle b}$, y determinar dónde converge la nueva serie de energía. Si la región contiene puntos que no están ${displaystyle Ucup V}$, entonces habremos continuado analíticamente ${displaystyle f}$ incluso más lejos. This particular ${displaystyle f}$ se puede continuar analíticamente hasta el plano complejo pinchado ${displaystyle mathbb {C} setminus {0}$

Definición formal de germen

La serie de potencias definida a continuación se generaliza mediante la idea de un germen. La teoría general de la continuación analítica y sus generalizaciones se conoce como teoría de la gavilla. Dejar

${displaystyle f(z)=sum _{k=0}{infty }alpha _{k}(z-z_{0})}{k}$

sea una serie de potencias convergentes en el disco D_r(z₀), r > 0, definido por

${displaystyle D_{0}={zinmathbb {C}:$.

Tenga en cuenta que sin pérdida de generalidad, aquí y más adelante, siempre supondremos que se eligió un máximo tal r, incluso si ese r es ∞. También tenga en cuenta que sería equivalente comenzar con una función analítica definida en un pequeño conjunto abierto. Decimos que el vector

${displaystyle g=(z_{0},alpha _{0},alpha _{1},alpha _{2},ldots)}$

es un germen de f. La base g₀ de g es z₀, la raíz de g es (α₀, α₁, α₂,...) y la superior g₁ de g es α₀. La parte superior de g es el valor de f en z₀.

Cualquier vector g =z₀, α₀, α₁,...) es un germen si representa una serie de potencia de una función analítica alrededor z₀ con algún radio de convergencia r ■ 0. Por lo tanto, podemos hablar con seguridad del conjunto de gérmenes ${displaystyle {Mathcal {}}}$.

La topología del conjunto de gérmenes

Vamos g y h sean gérmenes. Si ${displaystyle Silencio.$ Donde r es el radio de convergencia de g y si la serie de potencia definida por g y h especificar funciones idénticas en la intersección de los dos dominios, entonces decimos que h se genera por (o compatible con) g, y escribimos g ≥ h. Esta condición de compatibilidad no es transitiva, simétrica ni antisimétrica. Si extendemos la relación por transitividad, obtenemos una relación simétrica, que es por lo tanto también una relación de equivalencia en los gérmenes (pero no un pedido). Esta extensión por transitividad es una definición de continuación analítica. La relación de equivalencia será denotada ${displaystyle cong }$.

Podemos definir una topología en ${displaystyle {Mathcal {}}}$. Vamos r Y dejar

${displaystyle U_{r}(g)={hin {fnMitcal {G}:ggeq h, habitg_{0}-h_{0}$

Los juegos U_r()g), para todos r " 0 " ${displaystyle gin {fnMitcal {G}}$ definir una base de conjuntos abiertos para la topología sobre ${displaystyle {Mathcal {}}}$.

Un componente conectado ${displaystyle {Mathcal {}}}$ (es decir, una clase de equivalencia) se llama Sheaf. También observamos que el mapa definido por ${displaystyle phi _{g}(h)=h_{0}:U_{r}(g)to mathbb {C}$ Donde r es el radio de convergencia de gEs un gráfico. El conjunto de estas tablas forma un atlas para ${displaystyle {Mathcal {}}}$, por lo tanto ${displaystyle {Mathcal {}}}$ es una superficie Riemann. ${displaystyle {Mathcal {}}}$ a veces se llama función analítica universal.

Ejemplos de continuación analítica

${displaystyle L(z)=sum _{k=1}{infty }{frac {(-1)^{k+1} {k}} {k}} {k}} {k}}} {cH}} {cH}}} {c}}} {c}}}} {cH}}} {c}}}}}} {c}}}}}}}} {c}}}}}}} {c}}}} {c}}}}} {c}}}}}}} {c}}}}}}}}} {c}}}}}}}}} {c}}}}}}}} {c}}}}} {c}}}}}}}}}}} {c}}}}}}}}}}} {c}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$

es una serie de potencias correspondiente al logaritmo natural cerca de z = 1. Esta serie de potencias se puede convertir en un germen

${displaystyle g=left(1,0,1,-{frac {1}{2}},{frac {1}{3}}},-{frac {1}{4}},{frac {1}{5}},-{frac {1}{6}}}}}}ldots right)}}}}} {ldots}}} {f}} {f}}}}}}} {f}}}} {f}}} {f} {f} {f}}}} {f}}}}}}}} {f}}}}}}} {f}}}}}}} {f}}}} {f}}}}}}} {f}}}}}}}}}}}}}}}} {f} {f}}}}} {f}}}}}}}}}}}}}}}}}} {f}}}}}}$

Este germen tiene un radio de convergencia de 1, por lo que le corresponde una gavilla S. Esta es la gavilla de la función logaritmo.

El teorema de unicidad para las funciones analíticas también se extiende a los haces de funciones analíticas: si el haz de una función analítica contiene el germen cero (es decir, el haz es uniformemente cero en alguna vecindad), entonces todo el haz es cero. Armados con este resultado, podemos ver que si tomamos cualquier germen g del haz S de la función logaritmo, como se describe arriba, y lo convertimos en una serie de potencias < i>f(z) entonces esta función tendrá la propiedad de que exp(f(z)) = z. Si hubiéramos decidido usar una versión del teorema de la función inversa para funciones analíticas, podríamos construir una amplia variedad de inversas para el mapa exponencial, pero descubriríamos que todas están representadas por algún germen en S. En ese sentido, S es el "único verdadero inverso" del mapa exponencial.

En la literatura más antigua, los haces de funciones analíticas se denominaban funciones multivaluadas. Ver gavilla para el concepto general.

Límite natural

Supongamos que una serie de potencias tiene un radio de convergencia r y define una función analítica f dentro de ese disco. Considere puntos en el círculo de convergencia. Un punto para el que existe una vecindad en la que f tiene una extensión analítica es regular, en caso contrario singular. El círculo es un límite natural si todos sus puntos son singulares.

Más generalmente, podemos aplicar la definición a cualquier dominio conectado abierto en el que f sea analítico, y clasificar los puntos del límite del dominio como regulares o singulares: el límite del dominio es entonces un límite natural si todos los puntos son singulares, en cuyo caso el dominio es un dominio de holomorfia.

Ejemplo I: una función con un límite natural en cero (la función zeta prima)

Para ${displaystyle Re (s)}$ definimos la llamada función zeta primitiva, ${displaystyle P(s)}$, para ser

${displaystyle P(s):=sum _{text{ prime}p^{-s}}$

Esta función es análoga a la forma summatoria de la función Riemann zeta cuando ${displaystyle Re (s)}$ en tanto que es la misma función summatoria que ${displaystyle zeta (s)}$, excepto con índices restringidos sólo a los números primos en lugar de tomar la suma sobre todos los números naturales positivos. La función zeta primitiva tiene una continuación analítica a todo complejo s tales que ${displaystyle 0 realizadasRe (s) realizadas1}$, un hecho que sigue de la expresión ${displaystyle P(s)}$ por los logaritmos de la función Riemann zeta como

${displaystyle P(s)=sum _{ngeq 1}mu (n){frac {log zeta (ns)}{n}}}$

Desde ${displaystyle zeta (s)}$ tiene un polo simple, no extraíble en ${displaystyle s:=1}$, entonces se puede ver que ${displaystyle P(s)}$ tiene un poste simple en ${displaystyle s:={tfrac {1}{k},forall kin mathbb {Z}$. Desde el conjunto de puntos

${displaystyle operatorname {Sing} ¿Por qué? {1}{2},{frac {1}} {frac {1}{4},ldots right}}$

tiene punto de acumulación 0 (el límite de la secuencia como ${displaystyle kmapsto infty}$), podemos ver que cero forma un límite natural para ${displaystyle P(s)}$. Esto implica que ${displaystyle P(s)}$ no tiene continuación analítica para s izquierda de (o a) cero, es decir, no hay continuación posible para ${displaystyle P(s)}$ cuando ${displaystyle 0geq Re (s)}$. Como observación, este hecho puede ser problemático si estamos realizando un complejo contorno integral a lo largo de un intervalo cuyas partes reales son simétricas sobre cero, digamos ${displaystyle I_{F}subseteq mathbb {C} {text{such that} Re (s)in (-C,C),forall sin I_{F}$ para algunos ${displaystyle C confiar0}$, donde el integrador es una función con denominador que depende de ${displaystyle P(s)}$ de una manera esencial.

Ejemplo II: Una serie lagunar típica (límite natural como subconjuntos del círculo unitario)

Para los enteros ${displaystyle cgeq 2}$, definimos la serie lacunaria de orden c por la expansión de la serie de energía

${displaystyle {mathcal {L}_{c}(z):=sum _{ngeq 1}z^{c^{n}}}, "Princez"$

Claramente, desde ${displaystyle c^{n+1}=ccdot c^{n}$ hay una ecuación funcional para ${fnMicrosoft Sans Serif}$ para cualquier z satisfacción ${displaystyle Silencioz habit1}$ dado por ${displaystyle {mathcal {}_{c}(z)=z^{c}+{mathcal {L}_{c}(z^{c}}}}$. Tampoco es difícil ver eso para cualquier entero ${displaystyle mgeq 1}$, tenemos otra ecuación funcional para ${fnMicrosoft Sans Serif}$ dado por

${fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMithcal {L}_ {c}(z^{m}}),portodos los que vivieron.}$

Para cualquier número natural positivo c, la función de la serie lacunaria se divierte en ${displaystyle z=1}$. Consideramos la cuestión de la continuación analítica de ${fnMicrosoft Sans Serif}$ a otros complejos z tales que ${displaystyle Никованиных.}$ Como veremos, por cualquiera ${displaystyle ngeq 1}$, la función ${fnMicrosoft Sans Serif}$ divergencias en el ${displaystyle c^{n}$- las raíces de la unidad. Por lo tanto, ya que el conjunto formado por todas estas raíces es denso en el límite del círculo de la unidad, no hay continuación analítica de ${fnMicrosoft Sans Serif}$ complejo z cuyo módulo supera uno.

La prueba de este hecho se generaliza a partir de un argumento estándar para el caso donde ${displaystyle c:=2.}$ Es decir, para los enteros ${displaystyle ngeq 1}$, vamos

${fnMicrosoft Sans Serif} mathbb {D} cup partial {mathbb {D}:$

Donde ${displaystyle mathbb {}$ denota el disco de unidad abierta en el plano complejo y ${fnMicrosoft Sans Serif}$, es decir, hay ${displaystyle c^{n}$ números complejos distintos z que se encuentran en o dentro del círculo de la unidad tal que ${displaystyle z^{c^{n}=1}$. Ahora la parte clave de la prueba es utilizar la ecuación funcional para ${fnMicrosoft Sans Serif}$ cuando ${displaystyle Silencioz habit1}$ para mostrar eso

${displaystyle forall zin {fnMitcal {R}_{c,n},qquad {mathcal {L}_{c}(z)=sum ¿Por qué? ¿Qué?$

Así, para cualquier arco en el límite del círculo de la unidad, hay un número infinito de puntos z dentro de este arco tal que ${fnMicrosoft Sans Serif}$. Esta condición equivale a decir que el círculo ${displaystyle ¿Qué?$ forma un límite natural para la función ${fnMicrosoft Sans Serif}$ para cualquier elección fija ${displaystyle cin mathbb {Z} quad c confía1.}$ Por lo tanto, no hay continuación analítica para estas funciones más allá del interior del círculo de unidad.

Teorema de la monodromía

El teorema de la monodromía da una condición suficiente para la existencia de una continuación analítica directa (es decir, una extensión de una función analítica a una función analítica en un conjunto mayor).

Suppose ${displaystyle Dsubset mathbb {C}$ es un conjunto abierto y f una función analítica en D. Si G es un dominio simplemente conectado que contiene D, tal que f tiene una continuación analítica a lo largo de cada camino en G, comenzando desde un punto fijo a dentro D, entonces f tiene una continuación analítica directa G.

En el lenguaje anterior, esto significa que si G es un dominio simplemente conexo, y S es una gavilla cuyo conjunto de puntos base contiene G, entonces existe una función analítica f sobre G cuyos gérmenes pertenecen a S.

Teorema de la brecha de Hadamard

Para una serie de potencias

${displaystyle f(z)=sum ¿Qué? - Sí.$

con

${displaystyle liminf _{kto infty }{frac {n_{k+1} {n_{k}}}} {n_{k}}}}}} {n_{n_}}}}}}}}}}}}} {n_{k}}}}}}}}}}} {n_}}}}}}}}}} {n_{n_ k}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {n}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {n}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$

el círculo de convergencia es un límite natural. Tal serie de potencias se llama lacunaria. Este teorema ha sido sustancialmente generalizado por Eugen Fabry (ver el teorema de la brecha de Fabry) y George Pólya.

Teorema de Pólya

Dejar

${displaystyle f(z)=sum _{k=0}{infty }alpha _{k}(z-z_{0})}{k}$

siendo una serie de potencias, entonces existe ε_k ∈ {−1, 1} tal que

${displaystyle f(z)=sum _{k=0}{infty Varepsilon...$

tiene el disco de convergencia de f alrededor de z₀ como límite natural.

La demostración de este teorema utiliza el teorema de la brecha de Hadamard.

Un teorema útil: una condición suficiente para la continuación analítica de los enteros no positivos

En la mayoría de los casos, si existe una continuación analítica de una función compleja, es dada por una fórmula integral. El próximo teorema, siempre que se cumplan sus hipótesis, proporciona una condición suficiente bajo la cual podemos continuar una función analítica desde sus puntos convergentes a lo largo de los hechos positivos hasta arbitrarios ${displaystyle sin mathbb {C}$ (con la excepción de los polos finitos). Además, la fórmula da una representación explícita para los valores de la continuación a los enteros no positivos expresados exactamente por los derivados de orden superior (integer) de la función original evaluada a cero.

Hipótesis del teorema

Requerimos que una función ${displaystyle F:mathbb {R} ^{+}to mathbb {C}$ satisface las siguientes condiciones para aplicar el teorema en la continuación de esta función indicada a continuación:

• (T-1). La función debe tener derivados continuos de todos los pedidos, es decir, ${displaystyle ¿Qué?$. En otras palabras, para cualquier entero ${displaystyle jgeq 1}$, el orden integral ${displaystyle j^{th}$ derivados ${displaystyle F^{(j)}(x)={frac {d^{(j)}{dx^{(j)}}}}[F(x)}}}}$ debe existir, ser continuo ${displaystyle mathbb {R}$, y por sí mismo ser diferente, para que todos los derivados de orden superior de F son funciones suaves x sobre los números reales positivos;
• (T-2). Requerimos que la función F es rápidamente disminuyendo en eso para todos ${displaystyle nin mathbb {Z}$ obtenemos el comportamiento limitante ${displaystyle t^{n}F(t)to 0}$ como t se hace sin límites, tendiendo al infinito;
• (T-3). La transformación de Mellin (reciprocal gamma-scaled) F existe para todo complejo s tales que ${displaystyle Re (s)}$ con excepción de ${displaystyle sin {zeta _{1}(F),zeta _{2}(F),ldotszeta _{k}(F)}}$ (o para todos) s con partes reales positivas excepto posiblemente en un número finito de polos excepcionales:

${fnMicrosoft Sans Serif} {1}{Gamma (s)}int _{0}{infty }t^{s}F(t){frac {dt}}},qquadleft perpetua{widetilde {mathcal {m} {F](s)derechoso)intente! {C}:Re (z)}setminus {zeta _{1}(F),ldotszeta _{k}(F)}.}$

La conclusión del teorema

Vamos F ser cualquier función definida en los reales positivos que satisface todas las condiciones (T1)-(T3) arriba. Luego la representación integral de la transformación de Mellin escalada F a s, denotado por ${fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}$, tiene una continuación meromorfa al plano complejo ${displaystyle mathbb {C} setminus {zeta _{1}(F),ldotszeta _{k}(F)}}$. Además, lo tenemos para cualquier no negativo ${displaystyle nin mathbb {Z}$, la continuación de F en el punto ${displaystyle S:=-n}$ se da explícitamente por la fórmula

${fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fn}fn}}equiv (-1)^{n}times {fn} {fn} {fn} {fn} {m}}} {fn} {fn}}}}m} {ss0}fn}sss}fn}fn}fn}ssssssssigualtod}fn}fn}fn}f}fn}fn}fn}fnh00}f}fn}fn}f}fn}nhnh00}fnh00}soy}n}nhn}soy}nh}fn}fnhnhn}nhnhnh}nhnh00}fnhnh}n}nhn$

Ejemplos

Ejemplo I: La conexión de la función zeta de Riemann con los números de Bernoulli

Podemos aplicar el teorema a la función

${displaystyle F_{zeta }(x):={frac {x}{e^{x}=sum ¿Por qué? ¡Oh!$

que corresponde a la función generadora exponencial de los números Bernoulli, ${displaystyle B_{n}$. Para ${displaystyle Re (s)}$, podemos expresar ${displaystyle zeta (s)={widetilde {mathcal {M}}[F_{zeta }(s)}$, ya que podemos calcular que la siguiente fórmula integral para los poderes recíprocos de los enteros ${displaystyle ngeq 1}$ para s en esta gama:

${displaystyle {frac {fn} {fn}}={frac} {fnK}} {1}{Gamma (s)}int ¿Por qué?$

Ahora ya que el componente de la última ecuación es una función uniformemente continua de t para cada entero positivo n, tenemos una representación integral para ${displaystyle zeta (s)}$ siempre ${displaystyle Re (s)}$ dado por

${displaystyle zeta (s)=sum _{ngeq 1}n^{-s}={frac {1}{Gamma (s)}int ¿Por qué? 1}e^{-nt}right)t^{s-1}dt={frac {1}{Gamma (s)}int ¿Qué? ¿Qué?$

Cuando realizamos la integración por partes en el Mellin transform integral para esto ${displaystyle F_{zeta }(x)}$, también obtenemos la relación que

${displaystyle zeta (s)={frac {1}{(s-1)}{widetilde {mathcal {}}}[F_{zeta }](s-1). }$

Además, desde entonces ${displaystyle e^{t}gg t^ {n}$ para cualquier poder polinomio de entero fijo t, nos encontramos con la hipótesis del teorema que requiere eso ${displaystyle lim _{tto +infty }t^{n}cdot F_{zeta }(t),forall nin mathbb {Z} {+}$. La aplicación estándar del teorema de Taylor a la función generadora ordinaria de los números de Bernoulli muestra que ${displaystyle F_{zeta}{(n)}(0)={frac ¡Tiempos! ¡No!$. En particular, por la observación hecha anteriormente para cambiar ${displaystyle smapsto s-1}$, y estos comentarios, podemos calcular los valores de los denominados ceros triviales de la función Riemann zeta (para ${displaystyle zeta (-2n)}$) y las constantes de orden integer negativo de valor racional, ${displaystyle zeta (-(2n+1)),ngeq 0}$, según la fórmula

${displaystyle zeta (-n)=-{frac {1}{n+1}{widetilde {fn1} {fn} {fn1} {fn1} {fn1} {fn} {fn}} {fn+1} {fn+1)}(0)={begin{cases}-{frac {1}{2}}, limitn=0;\\\infty recíprocan=1;\-{frac {B_{n+1}{n+1}}} {ngq} 2.end{cases}}$

Ejemplo II: Una interpretación de F como la función sumatoria de alguna sucesión aritmética

Supongamos que F es una función suave y suficientemente decreciente sobre los reales positivos que satisface la condición adicional de que

${displaystyle Delta [F](x-1)=F(x)-F(x-1)=:f(x),forall xin mathbb {Z} ^{+}$

En aplicación a contextos teóricos de números, consideramos tal F como la función sumatoria de la función aritmética f,

${displaystyle F(x):={sum _{ngeq x}{prime }f(n)}$

donde tomamos ${displaystyle F(x)=0,forall 0 seleccionado1}$ y la primera nota en la suma anterior corresponde a las convenciones estándar utilizadas para el teorema de Perron:

${displaystyle F_{f}(x):={sum _{nleq x}}{prime }f(n)={begin{cases}sum _{nleq [x]}f(n), limitxin mathbb {R} ^{+}setminus mathbb {Z};\sum _{nleq x}f(n)-{frac {f(x)}{2}}} {xin mathbb {R} ^{+}cap mathbb {Z}end{cases}}$

Estamos interesados en la continuación analítica de la DGF de f, o equivalentemente de la serie de Dirichlet sobre f en s,

${displaystyle D_{f}=sum _{ngeq 1}{frac {f(n)}{n^{s}}}}$

Típicamente, tenemos un valor particular del abscissa de la convergencia, ${displaystyle sigma _{0,f} Conf0}$, definido tal ${displaystyle D_{f}(s)}$ es absolutamente convergente para todo complejo s satisfacción ${displaystyle Re (s)}sigma _{0,f}$, y dónde ${displaystyle D_{f}(s)}$ se supone que tiene un poste en ${displaystyle s:=pm sigma _{0,f}$ y para que la serie Dirichlet inicial ${displaystyle D_{f}(s)}$ divergencias para todos s tales que ${displaystyle Re (s)leq sigma _{0,f}$. Se sabe que hay una relación entre la transformación de Mellin de la función summatoria de cualquier f a la continuación de su DGF ${displaystyle smapsto -s}$ de la forma:

${displaystyle D_{f}(s)={mathcal {M}[F]=int _{1}{infty }{frac {F_{f} {f}{x^{s+1}dx} {f} {f} {f}} {f}}}$

Es decir, siempre ${displaystyle D_{f}(s)}$ tiene una continuación al plano complejo dejado del origen, podemos expresar la función summatoria de cualquier f por la inversa transformación de Mellin del DGF f seguido s con partes reales menos que cero como:

${displaystyle F_{f}(x)={mathcal {M}}{-1}left[{mathcal {M}}[F_{f}](-s)right](x)={mathcal {M}^{-1}[D_{f}(-s)]}$

Podemos formar el DGF, o función generadora de Dirichlet, de cualquier f prescrita dada nuestra función objetivo suave F realizando la suma por partes como

${fnMicrosoft Sans Serif} {1}{Gamma (s)}int ¿Por qué? {1}{Gamma (s)}int _{Nto infty }left[F(N)e^{-Nt}+sum ¿Por qué? {1}{Gamma (s)}int ¿Por qué? {1}{Gamma (s)}int ¿Por qué? {1}{Gamma (s)}int ¿Por qué?$

Donde ${displaystyle {hat {f}(x)equiv {mathcal}[F](x)}$ es la transformación de Laplace-Borel F, que si

${displaystyle F(z):=sum _{ngeq 0}{frac ¡No!$

corresponde a la función generadora exponencial de alguna secuencia enumerada por ${displaystyle ¡No!$ (según lo prescrito por la expansión de la serie Taylor F sobre cero), entonces

${displaystyle {widetilde {F}(z)=sum _{ngeq 0}f_{n}z^{n}}$

es su forma de función generadora ordinaria sobre la secuencia cuyos coeficientes son enumerados por ${fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fn} {fnMicrosoft Sans Serif}$.

Entonces se sigue que si escribimos

${displaystyle G_{F}(x):={frac {x}{1-x}Fleft({frac {x}{1-x}}right)=sum _{ngeq 0}left(sum _{k=0}{n}{binom}{binom} ¿Qué?$

interpretada alternativamente como una variante firmada de la transformación binomial F, entonces podemos expresar el DGF como la siguiente transformación de Mellin en ${displaystyle - Sí.$:

${fnMicrosoft Sans Serif} {f} {f} {fnMitcal {f}[G_{F}](-s){mthcal {m}left[1-e^{-1/x}right]s)\\cH00={f} {fnMitcal {} {f} {fnh}}left(1-Gamma (s)right)end{aligned}}$

Por último, ya que la función gamma tiene una continuación meromorfa ${displaystyle mathbb {C} setminus mathbb {N}$, para todos ${displaystyle sin mathbb {C} setminus {0,1,2,ldots },}$ tenemos una continuación analítica del DGF para f a - de la forma

${displaystyle D_{f}(-s)=-{frac {1-Gamma (-s)}{mathcal {M}[G_{F}(s)} {cHFF} {cH00}}$

donde una fórmula para ${displaystyle D_{f}(-n)}$ para los enteros no negativos n se da de acuerdo a la fórmula en el teorema como

${f} {f} {f} {f}}ln}n}m}}left[left(1-e^{-1/x}right){frac {x}{1-x}}Fleft({frac {x}{1-x}{f} {derech}}derech}derech] Biggr Silencio.$

Además, siempre que la función aritmética f satisfizo ${displaystyle f(1)neq 1}$ para que su función inversa Dirichlet exista, el DGF de ${displaystyle f^{-1}$ continúa cualquiera ${displaystyle sin mathbb {C} cap {z:Re (z)in (-infty-sigma _{0,f})cup (sigma _{0,f},+infty)}}$, que es cualquier complejo s excluyendo s en una f-definido o dependiente de la aplicación f- específico, llamada tira crítica entre las líneas verticales ${displaystyle z=pm sigma _{0,f}$, y el valor de esta función inversa DGF cuando ${displaystyle Re (s)$ es dado por

${displaystyle D_{f^{-1} {-s)={begin{cases}0, recurnin mathbb {N} {S+1}{1-Gamma (-s)}{mathcal {fnMicrosoft Sans Serif}end{cases}}$

Continuar el DGF de la función inversa Dirichlet s dentro de esto f-definido tira crítica, debemos requerir algún conocimiento de una ecuación funcional para el DGF, ${displaystyle D_{f}(s)}$, que nos permite relacionar el s tal que la serie Dirichlet que define esta función inicialmente es absolutamente convergente a los valores de s dentro de esta tira —en esencia, una fórmula que proporciona que ${displaystyle D_{f}(s)=xi _{f}(s)times D_{f}(sigma _{0,f}-s)}$ es necesario definir el DGF en esta tira.