Contabilidad del crecimiento

Contabilidad del crecimiento es un procedimiento utilizado en economía para medir la contribución de diferentes factores al crecimiento económico y para calcular indirectamente la tasa de progreso tecnológico, medida como residual, en una economía. La contabilidad del crecimiento descompone la tasa de crecimiento de la producción total de una economía en la que se debe a los aumentos en la cantidad contribuyente de los factores utilizados, por lo general el aumento en la cantidad de capital y trabajo, y la que no puede ser explicada por cambios observables en la utilización de factores. La parte no explicada del crecimiento del PIB se considera entonces que representa aumentos en la productividad (obtener más producción con la misma cantidad de insumos) o una medida del progreso tecnológico ampliamente definido.

La técnica se ha aplicado a prácticamente todas las economías del mundo y un hallazgo común es que los niveles observados de crecimiento económico no pueden explicarse simplemente por cambios en el stock de capital en la economía o las tasas de crecimiento de la población y la fuerza laboral. De ahí que el progreso tecnológico juegue un papel fundamental en el crecimiento económico de las naciones, o en la falta de él.

Historia

Esta metodología fue introducida por Robert Solow y Trevor Swan en 1957. La contabilidad del crecimiento se propuso para la contabilidad de gestión en la década de 1980. pero no prosperaron como herramientas de gestión. La razón es clara. Las funciones de producción se entienden y formulan de manera diferente en la contabilidad del crecimiento y la contabilidad de gestión. En la contabilidad del crecimiento, la función de producción se formula como una función OUTPUT=F (INPUT), cuya formulación lleva a maximizar la relación de productividad promedio OUTPUT/INPUT. La productividad media nunca ha sido aceptada en la contabilidad de gestión (en los negocios) como un criterio de rendimiento o un objetivo a maximizar porque significaría el fin del negocio rentable. En cambio, la función de producción se formula como una función INGRESO = F (SALIDA-ENTRADA) que debe maximizarse. El nombre del juego es maximizar los ingresos, no maximizar la productividad o la producción.

Ejemplo abstracto

Incluir el aumento de la producción a causa de la tecnología y el aumento del capital (haga clic para ampliar)

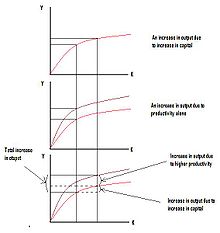
El modelo de contabilidad del crecimiento normalmente se expresa en forma de función de crecimiento exponencial. Como ejemplo abstracto, considere una economía cuya producción total (PIB) crece un 3% anual. En el mismo período su stock de capital crece al 6% anual y su fuerza de trabajo al 1%. La contribución de la tasa de crecimiento del capital a la producción es igual a la tasa de crecimiento ponderada por la participación del capital en la producción total y la contribución del trabajo viene dada por la tasa de crecimiento del trabajo ponderada por la participación del trabajo en el ingreso. Si la participación del capital en la producción es 1⁄3 , entonces la parte del trabajo es 2⁄3< /span> (asumiendo que estos son los dos únicos factores de producción). Esto significa que la parte del crecimiento de la producción que se debe a cambios en los factores es 0,06×(1⁄3)+.01×(2⁄3)=.027 o 2.7%. Esto significa que todavía hay un 0,3% del crecimiento de la producción que no se puede explicar. Este resto es el aumento en la productividad de los factores que ocurrió durante el período, o la medida del progreso tecnológico durante este tiempo.

Ejemplo específico

La contabilidad del crecimiento también se puede expresar en forma de modelo aritmético, que se utiliza aquí porque es más descriptivo y comprensible. El principio del modelo contable es simple. Las tasas de crecimiento ponderadas de los insumos (factores de producción) se restan de las tasas de crecimiento ponderadas de los productos. Debido a que el resultado contable se obtiene al restar, a menudo se le llama "residual". El residual a menudo se define como la tasa de crecimiento de la producción que no se explica por las tasas de crecimiento ponderadas por participación de los insumos.

Podemos utilizar los datos reales del proceso del modelo de producción para mostrar la lógica del modelo de contabilidad de crecimiento e identificar posibles diferencias en relación con el modelo de productividad. Cuando los datos de producción son los mismos en la comparación de modelos, las diferencias en los resultados contables se deben únicamente a los modelos contables. Obtenemos la siguiente contabilidad de crecimiento a partir de los datos de producción.

Cálculo del modelo de contabilidad de crecimiento

El procedimiento de contabilidad del crecimiento procede de la siguiente manera. Primero se calculan las tasas de crecimiento de la producción y las entradas dividiendo los números del Período 2 con los números del Período 1. Luego, los pesos de los insumos se calculan como porcentajes de insumos del insumo total (Período 1). Las tasas de crecimiento ponderadas (WG) se obtienen ponderando las tasas de crecimiento con los pesos. El resultado contable se obtiene restando las tasas de crecimiento ponderadas de los insumos a la tasa de crecimiento del producto. En este caso el resultado contable es 0,015 lo que implica un crecimiento de la productividad del 1,5%.

Observamos que el modelo de productividad informa un crecimiento de la productividad del 1,4 % a partir de los mismos datos de producción. La diferencia (1,4% versus 1,5%) se debe al diferente volumen de producción utilizado en los modelos. En el modelo de productividad, el volumen de insumos se utiliza como medida del volumen de producción, lo que da una tasa de crecimiento de 1,063. En este caso, la productividad se define de la siguiente manera: volumen de producción por unidad de volumen de entrada. En el modelo de contabilidad del crecimiento, el volumen de producción se utiliza como medida del volumen de producción, lo que da una tasa de crecimiento de 1,078. En este caso, la productividad se define de la siguiente manera: consumo de insumos por unidad de volumen de producción. El caso se puede verificar fácilmente con la ayuda del modelo de productividad utilizando la producción como volumen de producción.

El resultado contable del modelo de contabilidad de crecimiento se expresa como un número de índice, en este ejemplo 1,015, que representa el cambio de productividad promedio. Como se demostró anteriormente, no podemos sacar conclusiones correctas basadas en números de productividad promedio. Esto se debe a que la productividad se contabiliza como una variable independiente separada de la entidad a la que pertenece, es decir, la formación del ingreso real. Por lo tanto, si comparamos en una situación práctica dos resultados de contabilidad de crecimiento del mismo proceso de producción, no sabemos cuál es mejor en términos de rendimiento de producción. Tenemos que conocer por separado los efectos de ingreso del cambio de productividad y el cambio de volumen de producción o su efecto de ingreso combinado para comprender cuál resultado es mejor y cuánto mejor.

Este tipo de error científico de nivel de análisis incorrecto ha sido reconocido y descrito hace mucho tiempo. Vygotsky advierte contra el riesgo de separar el tema bajo revisión del entorno total, la entidad de la cual el tema es una parte esencial. Al estudiar solo este tema aislado, es probable que terminemos con conclusiones incorrectas. Un segundo ejemplo práctico ilustra esta advertencia. Supongamos que estamos estudiando las propiedades del agua para apagar un incendio. Si enfocamos la revisión en pequeños componentes del conjunto, en este caso los elementos oxígeno e hidrógeno, llegamos a la conclusión de que el hidrógeno es un gas explosivo y el oxígeno es un catalizador en la combustión. Por lo tanto, su agua compuesta podría ser explosiva e inadecuada para apagar un incendio. Esta conclusión incorrecta surge del hecho de que los componentes han sido separados de la entidad.

Derivación técnica

La producción total de una economía se modela como producida por varios factores de producción, siendo el capital y el trabajo los principales en las economías modernas (aunque también se pueden incluir la tierra y los recursos naturales). Esto generalmente se captura mediante una función de producción agregada:

${displaystyle Y=F(A,K,L)}$

donde Y es la producción total, K es el stock de capital en la economía, L es la fuerza laboral (o población) y A es un "cajón de sastre" factor de tecnología, papel de las instituciones y otras fuerzas relevantes que mide cuán productivamente se utilizan el capital y la mano de obra en la producción.

La suposición estándar sobre la forma de la función F(.) es que es creciente en K, L, A (si aumenta la productividad o aumenta la cantidad de factores utilizados, obtiene más producción) y que es homogénea de grado uno, o en otras palabras, que hay rendimientos constantes a escala (lo que significa que si duplica tanto K como L obtiene el doble de producción). El supuesto de rendimientos constantes a escala facilita el supuesto de competencia perfecta que a su vez implica que los factores obtienen sus productos marginales:

${displaystyle {dY}/{dK}=MPK=r}$

${displaystyle {dY}/{dL}=MPL=w}$

donde MPK denota las unidades adicionales de producción producidas con una unidad adicional de capital y, de manera similar, para MPL. Los salarios pagados al trabajo se denotan por w y la tasa de ganancia o la tasa de interés real se denota por r. Tenga en cuenta que el supuesto de competencia perfecta nos permite tomar los precios como dados. Para simplificar, asumimos el precio unitario (es decir, P = 1) y, por lo tanto, las cantidades también representan valores en todas las ecuaciones.

Si diferenciamos totalmente la función de producción anterior obtenemos;

${displaystyle DY=F_{A}dA+F_{K}dK+F_{L}dL$

Donde ${displaystyle F_{i}$ denota el derivado parcial con respecto al factor i, o para el caso del capital y el trabajo, los productos marginales. Con competencia perfecta esta ecuación se convierte en:

${displaystyle dY=F_{A}dA+MPKdK+MPLdL=F_{A}dA+rdK+wdL}$

Si dividimos entre Y y convertimos cada cambio en tasas de crecimiento, obtenemos:

${displaystyle {dY}/{Y}=({F_{A}A/{Y})({dA}/{A})+(r{K}/{Y})*({dK}/{K})+(w{L}/{Y})*({dL}/{L})}}$

o denotando una tasa de crecimiento (cambio de porcentaje con el tiempo) de un factor como ${displaystyle G_{i}={di}/{i}$ Tenemos:

${displaystyle g_{Y}=({F_}A/{Y})*g_{A}+({rK}/{Y})*g_{K}+({wL}/{Y})*g_{L}}$

Entonces... ${displaystyle {}/{Y}$ es la parte del ingreso total que va al capital, que puede ser denotado como ${displaystyle alpha }$ y ${displaystyle {wL}/{Y}$ es la parte del ingreso total que va al trabajo, denotado por ${displaystyle 1-alpha }$. Esto nos permite expresar la ecuación anterior como:

${displaystyle G_{Y}={F_}A/{Y}*g_{A}+alpha *g_{K}+(1-alpha)*g_{L}$

En principio, los términos ${displaystyle alpha }$, ${displaystyle g_{Y}$, ${displaystyle G_{K}$ y ${displaystyle g_{L}$ son todos observables y pueden medirse utilizando métodos estándar de contabilidad de ingresos nacionales (con valores de capital medidos utilizando tasas de inversión mediante el método de inventario perpetuo). El término ${displaystyle {frac {fnK} {fnK} {fnMicrosoft} {f}} {f}} {f}}} {f}}}} {f}}}}}}} {f}}}}} {f}}} {f}}}}}} {f}}}}}}}}}}}}} {f}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}} {f}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}} {g_}}}}} {g_}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$ Sin embargo, no es directamente observable ya que capta el crecimiento tecnológico y la mejora de la productividad que no están relacionados con los cambios en el uso de factores. Este término se denomina generalmente crecimiento de la productividad de los factores residuales de Solow o Total. Reordenando ligeramente la ecuación anterior podemos medir esto como la porción del aumento de la producción total que no se debe al crecimiento (pesado) de las entradas de factor:

${displaystyle SolowResidual=g_{Y}-alpha *g_{K}-(1-alpha)*g_{L}$

Otra forma de expresar la misma idea es en términos per cápita (o por trabajador) en los que restamos la tasa de crecimiento de la fuerza laboral de ambos lados:

${displaystyle SolowResidual=g_{(Y/L)}-alpha *g_{(K/L)}}$

que establece que la tasa de crecimiento tecnológico es la parte de la tasa de crecimiento del ingreso per cápita que no se debe a la tasa de crecimiento (ponderada) del capital por persona.

Notas y referencias