Construcción neusis

En geometría, la neusis (νεῦσις; del griego antiguo νεύειν (neuein) 'inclinación hacia' plural: νεύσεις, neuseis) es un método de construcción geométrica que fue utilizado en la antigüedad por los matemáticos griegos.

Construcción geométrica

La construcción de neusis consiste en encajar un elemento de línea de longitud determinada (a) entre dos líneas dadas (l y m), de tal una forma en que el elemento de línea, o su extensión, pasa por un punto dado P. Es decir, un extremo del elemento de línea debe estar en l, el otro extremo en m, mientras que el elemento de línea está "inclinado" hacia P.

El punto P se llama polo de la neusis, la línea l la directriz o línea guía, y la línea m la línea de captura. La longitud a se llama diastema (en griego: διάστημα, lit.  'distancia').

Se puede realizar una construcción de neusis mediante una regla marcada que pueda girar alrededor del punto P (esto se puede hacer colocando un alfiler en el punto P y luego presionando la regla contra el alfiler). En la figura, un extremo de la regla está marcado con un ojo amarillo con punto de mira: este es el origen de la división de escala en la regla. Una segunda marca en la regla (el ojo azul) indica la distancia a desde el origen. El ojo amarillo se mueve a lo largo de la línea l, hasta que el ojo azul coincida con la línea m. La posición del elemento lineal así encontrado se muestra en la figura como una barra azul oscuro.

Trisección de un ángulo

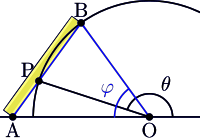
La neusis se puede utilizar para trisecar ángulos, de las siguientes maneras (con referencia a la imagen):

• Para un ángulo menor a 45°: Marque la línea recta con el radio del círculo, luego mueva su punto A sobre AO línea mientras se mantiene B en su borde, hasta que el final de la recta final toque el círculo – esto será en un punto más alto que B en el círculo (se verá como la imagen, excepto para B y P ser invertido). Entonces ángulo POA será igual a 60° menos el tercero del ángulo BOA. Como ejemplo, si BOA = 27°, entonces POA será igual a 60° – (27 ÷ 3)° = 51°.
• Para un ángulo más grande que 45° pero más pequeño que 90°: El principio es el mismo, excepto esta vez, A estará en una línea vertical que se extiende hacia arriba desde O.
• Para un ángulo superior a 90° pero menor a 135°: A sigue en una línea vertical que se extiende hacia arriba desde O. Sin embargo, deja punto C estar en cualquier lugar en la línea horizontal izquierda de O, y dejar punto D estar en cualquier lugar en la línea horizontal derecho de O. Angle POC será ahora igual a un tercio BOD.
• Para un ángulo superior a 135° pero más pequeño que 180°: Esta vez, el dibujo representa la situación con precisión, con punto D en cualquier lugar de la línea horizontal derecho de OAsí que Silencio = ∠DOB. AB es igual a OP = OB.

Uso de la neusis

Las Neuseis han sido importantes porque a veces proporcionan un medio para resolver problemas geométricos que no se pueden resolver únicamente con un compás y una regla. Ejemplos de ello son la trisección de cualquier ángulo en tres partes iguales y la duplicación del cubo. Matemáticos como Arquímedes de Siracusa (287-212 a. C.) y Pappus de Alejandría (290-350 d. C.) utilizaron libremente neuseis; Sir Isaac Newton (1642-1726) siguió su línea de pensamiento y también utilizó construcciones neusis. Sin embargo, poco a poco la técnica dejó de utilizarse.

Polígonos regulares

En 2002, A. Baragar mostró que cada punto edificable con marcado gobernante y brújula se encuentra en una torre de campos sobre ${\displaystyle \mathbb {Q}$, ${\displaystyle \mathbb {Q} =K_{0}\subset K_{1}\subset \dots \subset K_{n}=K}$, tal que el grado de la extensión en cada paso no es superior a 6. De todos los polígonos de primera potencia debajo del 128-gon, basta con demostrar que los 23-, 29-, 43-, 47-, 49-, 53-, 59-, 67-, 71-, 79-, 83-, 89-, 103-, 107-, 113-, 121- y 127-gons no se pueden construir con neusis. (Si es normal p-gon es constructible, entonces ${\displaystyle \zeta ¿Por qué? {2\c\cH00} - Sí.$ es constructible, y en estos casos p − 1 tiene un factor primario superior a 5.) 3-, 4-, 5-, 6-, 8-, 10-, 12-, 15-, 16-, 17-, 20-, 24-, 30-, 32-, 34-, 40-, 48-, 51-, 60-, 64-, 68-, 80-, 85-, 96-, 102-, 120- y 128-gones pueden construirse con sólo una recta y una brújula, Sin embargo, no se sabe en general si todos los quinéticos (polinomios de quinto orden) tienen raíces neusis-constructibles, que es relevante para los 11-, 25-, 31-, 41-, 61-, 101- y 125-gones. Benjamin y Snyder mostraron en 2014 que el 11-gon regular es neusis-constructible; los 25-, 31-, 41-, 61-, 101-, y 125-gones siguen siendo problemas abiertos. Más generalmente, la constructibilidad de todos los poderes de 5 más de 5 en sí mismo por marcado gobernante y brújula es un problema abierto, junto con todos los principios mayores de 11 de la forma p = 2^r3^s5^t + 1 donde t (todas las cifras principales que son mayores de 11 y iguales a una más de un número regular que es divisible por 10).

Popularidad menguante

T. L. Heath, el historiador de las matemáticas, ha sugerido que el matemático griego Enópides (c. 440 a.C. ) fue el primero en colocar construcciones con compás y regla encima de las neuseis. El principio de evitar neuseis siempre que sea posible puede haber sido difundido por Hipócrates de Quíos (c. 430 a.C.), originario de la misma isla que Enópides, y quién fue, hasta donde sabemos, el primero en escribir un libro de texto de geometría sistemáticamente ordenado. Cien años después de él, Euclides también evitó las neuseis en su muy influyente libro de texto, Los Elementos.

El siguiente ataque a la neusis se produjo cuando, a partir del siglo IV a.C., el idealismo de Platón ganó terreno. Bajo su influencia se desarrolló una jerarquía de tres clases de construcciones geométricas. Descendiendo de lo "abstracto y noble" para lo "mecánico y terrenal", las tres clases eran:

1. construcciones con líneas rectas y círculos solamente (compás y rectificado);
2. construcciones que además de este uso de secciones cónicas (países, parabolas, hiperbolas);
3. construcciones que necesitaban otros medios de construcción, por ejemplo neuseis.

Al final, el uso de neusis se consideró aceptable sólo cuando las otras dos categorías superiores de construcciones no ofrecían una solución. Neusis se convirtió en una especie de último recurso que sólo se invocaba cuando todos los demás métodos más respetables habían fracasado. El uso de neusis donde se podrían haber utilizado otros métodos de construcción fue calificado por el difunto matemático griego Pappus de Alejandría (c. 325 d.C.) como "un error nada despreciable" .