Constantin Carathéodory

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Matemático griego (1873-1950)

Constantin Carathéodory (griego: Κωνσταντίνος Καραθεοδωρή, romanizado: Konstantinos Karatheodori; 13 de septiembre de 1873 - 2 de febrero de 1950) fue un matemático griego que pasó la mayor parte de su carrera profesional en Alemania. Hizo importantes contribuciones al análisis real y complejo, el cálculo de variaciones y la teoría de la medida. También creó una formulación axiomática de la termodinámica. Carathéodory es considerado uno de los más grandes matemáticos de su época y el matemático griego más renombrado desde la antigüedad.

Orígenes

Carathéodory con su padre, Stephanos, en 1900.

Carathéodory (izquierda) se imaginaba sentado con su padre, hermano en derecho y hermana, Carlsbad 1898

Constantin Carathéodory nació en 1873 en Berlín de padres griegos y creció en Bruselas. Su padre Stephanos [tr], abogado, se desempeñó como embajador otomano en Bélgica, San Petersburgo. y Berlín. Su madre, Despina, de soltera Petrokokkinos, era de la isla de Quíos. La familia Carathéodory, originaria de Bosnochori o Vyssa, estaba bien establecida y respetada en Constantinopla, y sus miembros ocupaban muchos cargos gubernamentales importantes.

La familia Carathéodory pasó entre 1874 y 1875 en Constantinopla, donde vivía el abuelo paterno de Constantino, mientras su padre Stephanos estaba de permiso. Luego, en 1875, fueron a Bruselas cuando Stephanos fue nombrado allí embajador otomano. En Bruselas nació Julia, la hermana menor de Constantin. El año 1879 fue trágico para la familia ya que el abuelo paterno de Constantin murió ese año, pero mucho más trágico, la madre de Constantin, Despina, murió de neumonía en Cannes. La abuela materna de Constantin asumió la tarea de criar a Constantin y Julia en la casa de su padre en Bélgica. Contrataron a una criada alemana que enseñó a los niños a hablar alemán. Constantin ya era bilingüe en francés y griego en ese momento.

Constantin comenzó sus estudios formales en una escuela privada en Vanderstock en 1881. La dejó después de dos años y luego pasó un tiempo con su padre en una visita a Berlín, y también pasó los inviernos de 1883–84 y 1884–85 en la Riviera italiana. De regreso a Bruselas en 1885 asistió a una escuela primaria durante un año donde comenzó a interesarse por las matemáticas. En 1886, ingresó en la escuela secundaria Athénée Royal d'Ixelles y estudió allí hasta su graduación en 1891. Durante su estancia en esta escuela, Constantin ganó dos veces un premio como el mejor estudiante de matemáticas de Bélgica.

En esta etapa Carathéodory comenzó a formarse como ingeniero militar. Asistió a la École Militaire de Belgique de octubre de 1891 a mayo de 1895 y también estudió en la École d'Application de 1893 a 1896. En 1897 estalló una guerra entre el Imperio Otomano y Grecia. Esto puso a Carathéodory en una posición difícil ya que se puso del lado de los griegos, pero su padre sirvió en el gobierno del Imperio Otomano. Como era ingeniero de formación, le ofrecieron un trabajo en el servicio colonial británico. Este trabajo lo llevó a Egipto, donde trabajó en la construcción de la presa de Assiut hasta abril de 1900. Durante los períodos en que las obras tuvieron que pararse debido a las inundaciones, estudió matemáticas con algunos libros de texto que llevaba consigo, como el de Jordan. Texto de Cours d'Analyse y Salmon sobre la geometría analítica de secciones cónicas. También visitó la pirámide de Keops e hizo mediciones que redactó y publicó en 1901. También publicó un libro sobre Egipto ese mismo año que contenía una gran cantidad de información sobre la historia y geografía del país.

Estudios y carrera universitaria

Carathéodory estudió ingeniería en Bélgica en la Real Academia Militar, donde era considerado un estudiante carismático y brillante.

Carrera universitaria

1900 Estudios en la Universidad de Berlín.
1902 Graduación completa en la Universidad de Göttingen (1904 Ph.D, 1905 Habilitation)
1908 Dozent en Bonn
1909 Profesor Ordinario de la Escuela Técnica Superior Hannover.
1910 Profesor Ordinario de Breslau Technical High School.
1913 Profesora de la Universidad de Gotinga.
1919 Profesor de la Universidad de Berlín
1919 Elegido a la Academia de Ciencias de Prusia.
1920 Decano de la Universidad de Ionian de Smyrna (más tarde, Universidad del Egeo).
1922 Profesor de la Universidad de Atenas.
1922 Profesor en Atenas Polytechnic.
1924 Professor following Lindemann at University of Munich.
1938 Retirada de la cátedra. Trabajo continuo de la Academia de Ciencias de Baviera

Estudiantes de doctorado

Carathéodory tenía alrededor de 20 estudiantes de doctorado, entre ellos Hans Rademacher, conocido por su trabajo sobre análisis y teoría de números, y Paul Finsler, conocido por su creación del espacio de Finsler.

Contactos académicos en Alemania

Los contactos de Carathéodory en Alemania fueron muchos e incluyeron nombres tan famosos como: Hermann Minkowski, David Hilbert, Felix Klein, Albert Einstein, Edmund Landau, Hermann Amandus Schwarz, Lipót Fejér. Durante el difícil período de la Segunda Guerra Mundial, sus colaboradores más cercanos en la Academia de Ciencias de Baviera fueron Perron y Tietze.

Einstein, entonces miembro de la Academia de Ciencias de Prusia en Berlín, estaba trabajando en su teoría general de la relatividad cuando se puso en contacto con Carathéodory para pedirle aclaraciones sobre la ecuación de Hamilton-Jacobi y las transformaciones canónicas. Quería ver una derivación satisfactoria del primero y los orígenes del segundo. Einstein le dijo a Carathéodory que su derivación era "hermosa" y recomendó su publicación en el Annalen der Physik. Einstein empleó el primero en un artículo de 1917 titulado Zum Quantensatz von Sommerfeld und Epstein (Sobre el teorema cuántico de Sommerfeld y Epstein). Carathéodory explicó algunos detalles fundamentales de las transformaciones canónicas y remitió a Einstein a E.T. La Dinámica Analítica de Whittaker. Einstein estaba tratando de resolver el problema de las "líneas de tiempo cerradas" o las geodésicas correspondientes a la trayectoria cerrada de la luz y las partículas libres en un universo estático, que introdujo en 1917.

Landau y Schwarz estimularon su interés en el estudio del análisis complejo.

Contactos académicos en Grecia

Mientras estuvo en Alemania, Carathéodory mantuvo numerosos vínculos con el mundo académico griego, sobre los cuales se puede encontrar información detallada en el libro de Georgiadou. Estuvo directamente involucrado en la reorganización de las universidades griegas. Un amigo y colega especialmente cercano en Atenas fue Nicolaos Kritikos, quien había asistido a sus conferencias en Göttingen, luego lo acompañó a Esmirna y luego se convirtió en profesor en el Politécnico de Atenas. Kritikos y Carathéodory ayudaron al topólogo griego Christos Papakyriakopoulos a obtener un doctorado en topología en la Universidad de Atenas en 1943 en circunstancias muy difíciles. Mientras enseñaba en la Universidad de Atenas, Carathéodory tuvo como estudiante universitario a Evangelos Stamatis, quien posteriormente logró una distinción considerable como estudioso de los clásicos matemáticos griegos antiguos.

Obras

Cálculo de variaciones

En su tesis doctoral, Carathéodory mostró cómo ampliar las soluciones a casos discontinuos y estudió problemas isoperimétricos.

Anteriormente, entre mediados del siglo XVIII y mediados del siglo XIX, Leonhard Euler, Adrien-Marie Legendre y Carl Gustav Jacob Jacobi pudieron establecer condiciones necesarias pero insuficientes para la existencia de un mínimo relativo fuerte. En 1879, Karl Weierstrass añadió una cuarta cantidad que efectivamente garantiza que exista tal cantidad. Carathéodory construyó su método para derivar condiciones suficientes basándose en el uso de la ecuación de Hamilton-Jacobi para construir un campo de extremos. Las ideas están estrechamente relacionadas con la propagación de la luz en óptica. El método pasó a ser conocido como método de problemas variacionales equivalentes de Carathéodory o el camino real hacia el cálculo de variaciones. Una ventaja clave del trabajo de Carathéodory sobre este tema es que ilumina la relación entre el cálculo de variaciones y las ecuaciones diferenciales parciales. Permite derivaciones rápidas y elegantes de condiciones de suficiencia en el cálculo de variaciones y conduce directamente a la ecuación de Euler-Lagrange y la condición de Weierstrass. Publicó su Variationsrechnung und Partielle Differentialgleichungen Erster Ordnung (Cálculo de variaciones y ecuaciones diferenciales parciales de primer orden) en 1935.

Más recientemente, el trabajo de Carathéodory sobre el cálculo de variaciones y la ecuación de Hamilton-Jacobi se ha incorporado a la teoría del control óptimo y la programación dinámica. El método también se puede extender a integrales múltiples.

Geometría convexa

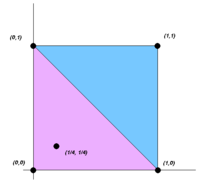
El teorema de Carathéodory en geometría convexa afirma que si un punto $x$ de $mathbb {R} ^{d}$ mentiras en el casco convexo de un conjunto $P$ , entonces $x$ se puede escribir como la combinación convexa de la mayoría $d+1$ puntos en $P$ . Es decir, hay un subconjunto $P'$ de $P$ consistente en $d+1$ o menos puntos tales que $x$ mentiras en el casco convexo $P'$ . Equivalentemente, $x$ mentiras en una $r$ -simplex con vértices en $P$ , donde $r leq d$ . El más pequeño $r$ que hace la última declaración válida para cada $x$ en el casco convexo P se define como Número de Carathéodory de $P$ . Dependiendo de las propiedades de $P$ , los bordes superiores inferiores a los proporcionados por el teorema de Carathéodory se pueden obtener.

Se le atribuye la autoría de la conjetura de Carathéodory que afirma que una superficie convexa cerrada admite al menos dos puntos umbilicales. En 2021, esta conjetura seguía sin demostrarse a pesar de haber atraído una gran cantidad de investigaciones.

Análisis real

Demostró un teorema de existencia para la solución de ecuaciones diferenciales ordinarias en condiciones de regularidad suaves.

Otro teorema suyo sobre la derivada de una función en un punto podría usarse para demostrar la regla de la cadena y la fórmula para la derivada de funciones inversas.

Análisis complejo

Amplió enormemente la teoría de la transformación conforme demostrando su teorema sobre la extensión del mapeo conforme hasta el límite de los dominios de Jordan. Al estudiar la correspondencia de límites, originó la teoría de los fines primos. Exhibió una prueba elemental del lema de Schwarz.

Carathéodory también estaba interesado en la teoría de funciones de múltiples variables complejas. En sus investigaciones sobre este tema buscó análogos de los resultados clásicos del caso monovariable. Él demostró que una bola en $mathbb{C}^2$ no es holomorfamente equivalente al bidisco.

Teoría de la medida

Se le atribuye el teorema de extensión de Carathéodory, que es fundamental para la teoría de la medida moderna. Posteriormente Carathéodory amplió la teoría de conjuntos a álgebras de Boole.

Termodinámica

La termodinámica había sido un tema muy querido para Carathéodory desde su estancia en Bélgica. En 1909, publicó una obra pionera "Investigaciones sobre los fundamentos de la termodinámica" en el que formuló la segunda ley de la termodinámica de forma axiomática, es decir, sin el uso de motores y refrigeradores de Carnot y únicamente mediante razonamiento matemático. Esta es otra versión más de la segunda ley, junto con las declaraciones de Clausius, Kelvin y Planck. La versión de Carathéodory atrajo la atención de algunos de los principales físicos de la época, incluidos Max Planck, Max Born y Arnold Sommerfeld. Según el estudio de termodinámica de Bailyn, el enfoque de Carathéodory se llama "mecánico", en lugar de "termodinámico" Max Born aclamó este "primer fundamento axiomáticamente rígido de la termodinámica" y expresó su entusiasmo en sus cartas a Einstein. Sin embargo, Max Planck tenía algunas dudas porque, si bien estaba impresionado por la destreza matemática de Carathéodory, no aceptaba que se tratara de una formulación fundamental, dada la naturaleza estadística de la segunda ley.

En su teoría simplificó los conceptos básicos, por ejemplo calor no es un concepto esencial sino derivado. Formuló el principio axiomático de irreversibilidad en termodinámica afirmando que la inaccesibilidad de los estados está relacionada con la existencia de entropía, donde la temperatura es la función de integración. La Segunda Ley de la Termodinámica se expresó mediante el siguiente axioma: "En las proximidades de cualquier estado inicial, hay estados a los que no se puede acercar arbitrariamente mediante cambios de estado adiabáticos". En este sentido acuñó el término accesibilidad adiabática.

Óptica

El trabajo de Carathéodory en óptica está estrechamente relacionado con su método de cálculo de variaciones. En 1926 dio una prueba estricta y general de que ningún sistema de lentes y espejos puede evitar la aberración, excepto el caso trivial de los espejos planos. En su trabajo posterior presentó la teoría del telescopio Schmidt. En su Geometrische Optik (1937), Carathéodory demostró la equivalencia de Huygens' principio y el principio de Fermat a partir del primero utilizando la teoría de las características de Cauchy. Sostuvo que una ventaja importante de su enfoque era que cubre las invariantes integrales de Henri Poincaré y Élie Cartan y completa la ley de Malus. Explicó que en sus investigaciones en óptica, Pierre de Fermat concibió un principio mínimo similar al enunciado por Héroe de Alejandría para estudiar la reflexión.

Histórica

(feminine)Did you mean:

During the Second World War Carathéodory edited two volumes of Euler 's Complete Works dealing with the Calculus of Variations which were submitted for publication in 1946.

La Universidad de Esmirna

En ese momento, Atenas era el único centro educativo importante en el área más amplia y tenía una capacidad limitada para satisfacer suficientemente la creciente necesidad educativa de la parte oriental del Mar Egeo y los Balcanes. Constantin Carathéodory, entonces profesor de la Universidad de Berlín, propuso la creación de una nueva universidad; las dificultades para la creación de una universidad griega en Constantinopla le llevaron a considerar otras tres ciudades: Salónica, Quíos y Esmirna.

Por invitación del Primer Ministro griego Eleftherios Venizelos, presentó un plan el 20 de octubre de 1919 para la creación de una nueva Universidad en Esmirna, en Asia Menor, que se llamaría Universidad Jónica de Esmirna. En 1920 Carathéodory fue nombrado Decano de la Universidad y participó de manera importante en el establecimiento de la institución, viajando por Europa para comprar libros y equipos. Sin embargo, la universidad nunca admitió estudiantes debido a la Guerra en Asia Menor que terminó con el Gran Incendio de Esmirna. Carathéodory logró salvar los libros de la biblioteca y sólo fue rescatado en el último momento por un periodista que lo llevó en un bote de remos hasta el acorazado Naxos que estaba esperando. Carathéodory trajo a Atenas parte de la biblioteca de la universidad y permaneció en Atenas, enseñando en la universidad y en la escuela técnica hasta 1924.

En 1924, Carathéodory fue nombrado profesor de matemáticas en la Universidad de Munich, cargo que ocupó hasta su jubilación en 1938. Posteriormente trabajó en la Academia de Ciencias de Baviera hasta su muerte en 1950.

La nueva Universidad Griega en el área más amplia de la región del Sudeste Mediterráneo, tal como la concibió originalmente Carathéodory, finalmente se materializó con el establecimiento de la Universidad Aristóteles de Tesalónica en 1925.

Talentos lingüísticos y oratorios

Carathéodory destacó en los idiomas, al igual que muchos miembros de su familia. El griego y el francés fueron sus primeros idiomas, y dominaba el alemán con tal perfección que sus escritos compuestos en idioma alemán son obras maestras estilísticas. Carathéodory también hablaba y escribía inglés, italiano, turco y lenguas antiguas sin ningún esfuerzo. Un arsenal lingüístico tan impresionante le permitió comunicarse e intercambiar ideas directamente con otros matemáticos durante sus numerosos viajes y amplió enormemente sus campos de conocimiento.

Mucho más que eso, Carathéodory era un preciado interlocutor de conversación para sus compañeros profesores en el Departamento de Filosofía de Munich. El respetado filólogo y profesor de lenguas antiguas alemán Kurt von Fritz elogió a Carathéodory alegando que de él se podía aprender muchísimo sobre la antigua y la nueva Grecia, la antigua lengua griega y las matemáticas helénicas. Von Fritz mantuvo numerosas discusiones filosóficas con Carathéodory.

El matemático envió a su hijo Stephanos y a su hija Despina a una escuela secundaria alemana, pero también recibieron instrucción adicional diaria en lengua y cultura griegas por parte de un sacerdote griego, y en casa les permitía hablar griego únicamente.

Carathéodory era un orador público talentoso y a menudo lo invitaban a dar discursos. En 1936, fue él quien entregó las primeras Medallas Fields en la reunión del Congreso Internacional de Matemáticos en Oslo, Noruega.

Legado

En 2002, en reconocimiento a sus logros, la Universidad de Munich nombró una de las salas de conferencias más grandes del instituto de matemáticas Sala de Conferencias Constantin-Carathéodory.

En la ciudad de Nea Vyssa, el hogar ancestral de Caratheodory, se encuentra un museo familiar único. El museo está situado en la plaza central de la ciudad, cerca de su iglesia, e incluye varios objetos personales de Karatheodory, así como cartas que intercambió con Albert Einstein. Se proporciona más información en el sitio web original del club, http://www.s-karatheodoris.gr.

Al mismo tiempo, las autoridades griegas hacía tiempo que tenían la intención de crear un museo en honor a Karatheodoris en Komotini, una ciudad importante de la región nororiental de Grecia, a más de 200 kilómetros de su ciudad natal. El 21 de marzo de 2009, los "Karatheodoris" El museo (Καραθεοδωρής) abrió sus puertas al público en Komotiní.

El coordinador del museo, Athanasios Lipordezis (Αθανάσιος Λιπορδέζης), ha señalado que el museo alberga manuscritos originales del matemático de unas 10.000 páginas, incluida la correspondencia con el matemático alemán Arthur Rosenthal para la algebraización de la medida. En la muestra, los visitantes también podrán ver los libros " Gesammelte mathematische Schriften Band 1,2,3,4 ", "Mass und ihre Algebraiserung", " Reelle Functionen Banda 1", " Zahlen/Punktionen Funktionen " y muchos otros. Se exponen cartas manuscritas de Carathéodory a Albert Einstein y Hellmuth Kneser, así como fotografías de la familia Carathéodory.

Se están realizando esfuerzos para equipar el museo con más exhibiciones.

Publicaciones

Artículos de revistas

Puede encontrar una lista completa de las publicaciones de artículos de revistas de Carathéodory en sus Obras completas (Ges. Math. Schr.). Las publicaciones notables son:

Über die kanonischen Veränderlichen in der Variationsrechnung der mehrfachen Integrale
Über das Schwarzsche Lemma bei analytischen Funktionen von zwei komplexen Veränderlichen
Über die diskontinuierlichen Lösungen in der Variationsrechnung. Diss. Göttingen Univ. 1904; Ges. Math. Schr. I 3–79.
Über die starken Maxima und Minima bei einfachen Integralen. Habilitationsschrift Göttingen 1905; Math. Annalen 62 1906 449–503; Ges. Math. Schr. I 80–142.
Untersuchungen über die Grundlagen der Thermodynamik, Math. Ann. 67 (1909) pp. 355–386; Ges. Math. Schr. II 131–166.
Über das lineare Mass von Punktmengen – eine Verallgemeinerung des Längenbegriffs., Gött. Nachr. (1914) 404–406; Ges. Math. Schr. IV 249–275.
Elementarer Beweis für den Fundamentalsatz der konformen Abbildungen. Schwarzsche Festschrift, Berlín 1914; Ges. Math. Schr.IV 249-275.
Zur Axiomatic der speziellen Relativitätstheorie. Sitzb. Preuss. Akad. Wiss. (1924) 12–27; Ges. Math. Schr. II 353–373.
Variationsrechnung in Frank P. " von Mises (eds): Die Differential= und Integralgleichungen der Mechanik und Physik, Braunschweig 1930 (Vieweg); Nueva York 1961 (Dover) 227–279; Ges. Math. Schr. I 312–370.
Entwurf für eine Algebraisierung des IntegralbegriffsSitzber. Bayer. Akad. Wiss. (1938) 27–69; Ges. Math. Schr. IV 302–342.

Libros

Carathéodory, Constantin (1918), Vorlesungen über reelle Funktionen (3rd ed.), Leipzig: Teubner, ISBN 978-0-8284-0038-1, MR 0225940 Reimpreso 1968 (Chelsea)
Representación Conformal, Cambridge 1932 (Cambridge Tracts in Mathematics and Physics)
Geometrische Optik, Berlín, 1937
Elementare Theorie des Spiegelteleskops von B. Schmidt (Teoría Elemental del Telescopio Reflecting de B. Schmidt), Leipzig Teubner, 1940 36 pp.; Ges. math. Schr. II 234–279
Funktionentheorie I, II, Basilea 1950, 1961 (Birkhäuser). Traducción en inglés: Teoría de Funciones de un Complejo Variable, 2 vols, New York, Chelsea Publishing Company, 3rd ed 1958
Mass und Integral und ihre Algebraisierung, Basilea 1956. Traducción en inglés, Medición e Integral y su Algebraización, Nueva York, Chelsea Publishing Company, 1963
Variationsrechnung und partielle Differentialgleichungen erster OrdnungLeipzig, 1935. Traducción en inglés siguiente referencia
Cálculo de Variaciones y Ecuaciones Diferenciales Parciales de la Primera Orden, 2 vols. I 1965, vol. II 1967 Holden-Day.
Gesammelte mathematische Schriften München 1954–7 (Beck) I–V.

Más resultados...