Constante gravitacional

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Constante física relativa a la fuerza gravitacional entre objetos a su masa y distancia

Valor de $G$	Dependencia
6.67430(15)×10^{−11 -}	N⋅m²⋅kg⁻²
6.67430(15)×10⁻⁸	dyn⋅cm²⋅g⁻²
4.30091727063)×10⁻³	pc⋅M⊙⁻¹⋅(km/s)²

La constante gravitacional

G

es una cantidad clave en la ley de Newton de la gravitación universal.

La constante gravitatoria (también conocida como la constante gravitacional universal, la constante newtoniana de gravitación o la constante gravitacional de Cavendish ), denotada por la letra mayúscula $G$ , es una constante física empírica involucrada en el cálculo de los efectos gravitatorios en Sir Isaac Newton&#39 en la ley de la gravitación universal y en la teoría de la relatividad general de Albert Einstein.

En la ley de Newton, es la constante de proporcionalidad que relaciona la fuerza gravitatoria entre dos cuerpos con el producto de sus masas y el inverso del cuadrado de su distancia. En las ecuaciones de campo de Einstein, cuantifica la relación entre la geometría del espacio-tiempo y el tensor de energía-momento (también conocido como tensor de tensión-energía).

El valor medido de la constante se conoce con cierta certeza hasta cuatro dígitos significativos. En unidades SI, su valor es aproximadamente 6.674×10⁻¹¹ m³⋅kg⁻¹⋅s⁻².

La notación moderna de la ley de Newton que implica $G$ fue introducida en la década de 1890 por C. V. Boys. La primera medición implícita con una precisión de alrededor del 1% se atribuye a Henry Cavendish en un experimento de 1798.

Definición

Según la ley de gravitación universal de Newton, la fuerza de atracción ( $F$ ) entre dos cuerpos puntuales es directamente proporcional a el producto de sus masas ( $m 1$ y $m 2$ ) e inversamente proporcional al cuadrado de la distancia, $r$ , entre sus centros de masa:

{displaystyle F=G{frac {m_{1}m_{2}}{r^{2}}}.}

G

g

M_oplus

{displaystyle r_{oplus }}

{displaystyle g={frac {GM_{oplus }}{r_{oplus }^{2}}}.}

La constante gravitatoria aparece en las ecuaciones de campo de la relatividad general de Einstein,

{displaystyle G_{mu nu }+Lambda g_{mu nu }=kappa T_{mu nu },,}

G μ

▪

g μ

T μ

κ

{displaystyle kappa ={frac {8pi G}{c^{4}}}approx 2.076647442844times 10^{-43}mathrm {,N^{-1}}.}

Valor e incertidumbre

La constante gravitatoria es una constante física que es difícil de medir con gran precisión. Esto se debe a que la fuerza gravitacional es una fuerza extremadamente débil en comparación con otras fuerzas fundamentales a escala de laboratorio.

En unidades SI, el valor de la constante gravitacional recomendado por el Comité de Datos para la Ciencia y la Tecnología (CODATA) de 2018 (con la incertidumbre estándar entre paréntesis) es:

{displaystyle G=6.67430(15)times 10^{-11}{rm { m^{3}{cdot }kg^{-1}{cdot }s^{-2}}}}

Esto corresponde a una incertidumbre estándar relativa de 2.2×10⁻⁵ (22 ppm).

Unidades naturales

La constante gravitacional es una constante definitoria en algunos sistemas de unidades naturales, particularmente en sistemas de unidades geometrizados, como las unidades de Planck y las unidades de Stoney. Cuando se expresa en términos de tales unidades, el valor de la constante gravitatoria generalmente tendrá un valor numérico de 1 o un valor cercano. Debido a la incertidumbre significativa en el valor medido de G en términos de otras constantes fundamentales conocidas, aparecerá un nivel similar de incertidumbre en el valor de muchas cantidades cuando se expresen en dicho sistema de unidades.

Mecánica orbital

En astrofísica es conveniente medir distancias en parsecs (pc), velocidades en kilómetros por segundo (km/s) y masas en unidades solares $M ⊙$ . En estas unidades, la constante gravitatoria es:

{displaystyle Gapprox 4.3009times 10^{-3} {mathrm {pc{cdot }(km/s)^{2}} ,M_{odot }}^{-1}.}

{displaystyle Gapprox 1.90809times 10^{5}mathrm { (km/s)^{2}} ,R_{odot }M_{odot }^{-1}.}

P

{displaystyle GM={frac {3pi V}{P^{2}}},}

V

{displaystyle P^{2}={frac {3pi }{G}}{frac {V}{M}}approx 10.896,mathrm {h^{2}{cdot }g{cdot }cm^{-3},} {frac {V}{M}}.}

Esta forma de expresar $G$ muestra la relación entre la densidad promedio de un planeta y el período de un satélite que orbita justo sobre su superficie.

Para órbitas elípticas, aplicando la 3.ª ley de Kepler, expresada en unidades características de la órbita terrestre:

{displaystyle G=4pi ^{2}mathrm { AU^{3}{cdot }yr^{-2}} M^{-1}approx 39.478mathrm { AU^{3}{cdot }yr^{-2}} M_{odot }^{-1},}

donde la distancia se mide en términos del semieje mayor de la órbita de la Tierra (la unidad astronómica, AU), el tiempo en años y la masa en la masa total del sistema en órbita ( $M = M ☉ + M Tierra + M ☾$ ).

La ecuación anterior es exacta solo dentro de la aproximación de la órbita de la Tierra alrededor del Sol como un problema de dos cuerpos en la mecánica newtoniana, las cantidades medidas contienen correcciones de las perturbaciones de otros cuerpos en el sistema solar y de relatividad general.

Desde 1964 hasta 2012, sin embargo, se usó como la definición de la unidad astronómica y, por lo tanto, se mantuvo por definición:

{displaystyle 1 mathrm {AU} =left({frac {GM}{4pi ^{2}}}mathrm {yr} ^{2}right)^{frac {1}{3}}approx 1.495979times 10^{11} mathrm {m}.}

1.495978707×10¹¹m

La cantidad $GM$ , el producto de la constante gravitacional y la masa de un cuerpo astronómico dado, como el Sol o la Tierra, se conoce como el parámetro gravitatorio estándar (también denominado $μ$ ). El parámetro gravitacional estándar $GM$ aparece como se indica arriba en la ley de gravitación universal de Newton, así como en fórmulas para la desviación de la luz causada por lente gravitacional, en las leyes de movimiento planetario de Kepler y en la fórmula para la velocidad de escape.

Esta cantidad brinda una conveniente simplificación de varias fórmulas relacionadas con la gravedad. El producto $GM$ se conoce con mucha más precisión que cualquiera de los factores.

Valores para MM
Cuerpo	$μ = MM$	Valor	Incertidumbre relativa
Sol	$G M ☉$	1.32712440018(8)×10²⁰m³⋅s⁻²	6×10^{−11 -}
Tierra	$G M Tierra$	3.986004418(8)×10¹⁴m³⋅s⁻²	2×10⁻⁹

Los cálculos de mecánica celeste también se pueden realizar utilizando las unidades de masas solares, días solares medios y unidades astronómicas en lugar de las unidades SI estándar. Para este propósito, la constante gravitatoria gaussiana ha sido históricamente de uso generalizado, $k$ = 0.01720209895, que expresa la velocidad angular media del sistema Sol-Tierra medida en radianes por día. El uso de esta constante, y la definición implícita de la unidad astronómica discutida anteriormente, ha sido desaprobada por la IAU desde 2012.

Historial de medición

Historia temprana

La existencia de la constante está implícita en la ley de gravitación universal de Newton tal como se publicó en la década de 1680 (aunque su notación es $G$ data de la década de 1890), pero no se calcula en su Philosophiæ Naturalis Principia Mathematica donde postula la ley de gravitación del inverso del cuadrado. En los Principia, Newton consideró la posibilidad de medir la fuerza de la gravedad midiendo la desviación de un péndulo en las proximidades de una gran colina, pero pensó que el efecto sería demasiado pequeño para ser medible.. Sin embargo, tuvo la oportunidad de estimar el orden de magnitud de la constante cuando supuso que "la densidad media de la tierra podría ser cinco o seis veces mayor que la densidad del agua", lo que equivale a una constante gravitatoria del orden:

G

. (6,7)±0.6)×10^{−11 -}m³⋅kg⁻¹⋅s⁻²

Pierre Bouguer y Charles Marie de La Condamine intentaron una medición en 1738 en su "expedición peruana". Bouguer minimizó la importancia de sus resultados en 1740, sugiriendo que el experimento al menos había demostrado que la Tierra no podía ser una cáscara hueca, como habían sugerido algunos pensadores de la época, incluido Edmond Halley.

El experimento de Schiehallion, propuesto en 1772 y completado en 1776, fue la primera medición exitosa de la densidad media de la Tierra y, por lo tanto, indirectamente de la constante gravitatoria. El resultado informado por Charles Hutton (1778) sugirió una densidad de 4,5 g/cm³ (4+ 1/2 veces la densidad del agua), alrededor de 20 % por debajo del valor moderno. Esto condujo inmediatamente a estimaciones sobre las densidades y masas del Sol, la Luna y los planetas, enviadas por Hutton a Jérôme Lalande para incluirlas en sus tablas planetarias. Como se discutió anteriormente, establecer la densidad promedio de la Tierra es equivalente a medir la constante gravitatoria, dado el radio medio de la Tierra y la aceleración gravitacional media en la superficie de la Tierra, estableciendo

{displaystyle G=g{frac {R_{oplus }^{2}}{M_{oplus }}}={frac {3g}{4pi R_{oplus }rho _{oplus }}}.}

G

8×10^{−11 -}m³⋅kg⁻¹⋅s⁻²

Diagrama de balance de torsión utilizado en el experimento de Cavendish realizado por Henry Cavendish en 1798, para medir G, con la ayuda de una polea, bolas grandes colgadas de un marco fueron rotadas en posición junto a las bolas pequeñas.

La primera medición directa de la atracción gravitatoria entre dos cuerpos en el laboratorio se realizó en 1798, setenta y un años después de la muerte de Newton, por Henry Cavendish. Determinó un valor para $G$ implícitamente, usando una balanza de torsión inventada por el geólogo Rev. John Michell (1753). Utilizó una viga de torsión horizontal con bolas de plomo cuya inercia (en relación con la constante de torsión) podía saber cronometrando la oscilación de la viga. Su débil atracción por otras bolas colocadas a lo largo de la viga fue detectable por la desviación que causó. A pesar de que el diseño experimental se debe a Michell, el experimento ahora se conoce como el experimento de Cavendish por su primera ejecución exitosa por parte de Cavendish.

El objetivo declarado de Cavendish era "pesar la Tierra", es decir, determinar la densidad media de la Tierra y la masa de la Tierra. Su resultado, ρ_🜨 = 5,448(33) g ·cm⁻³, corresponde al valor de $G$ = 6.74(4)×10⁻¹¹ m³⋅kg⁻¹⋅s⁻². Es sorprendentemente preciso, aproximadamente un 1 % por encima del valor moderno (comparable a la incertidumbre estándar declarada del 0,6 %).

Siglo XIX

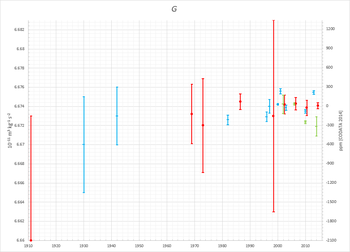
La precisión del valor medido de $G$ ha aumentado solo modestamente desde el experimento original de Cavendish. $G$ es bastante difícil de medir porque la gravedad es mucho más débil que otras fuerzas fundamentales y un aparato experimental no puede separarse de la influencia gravitacional de otros cuerpos.

Las mediciones con péndulos fueron realizadas por Francesco Carlini (1821, 4,39 g/cm³), Edward Sabine (1827, 4,77 g/cm³), Carlo Ignazio Giulio (1841, 4,95 g/cm³) y George Biddell Airy (1854, 6,6 g/cm³).

El experimento de Cavendish fue repetido por primera vez por Ferdinand Reich (1838, 1842, 1853), quien encontró un valor de 5,5832(149) g·cm⁻³, que en realidad es peor que el resultado de Cavendish, que difiere del valor moderno en un 1,5 %. Cornu y Baille (1873), encontraron 5,56 g·cm⁻³.

El experimento de Cavendish resultó en mediciones más confiables que los experimentos de péndulo del "Schiehallion" (deflexión) tipo o "peruano" (período en función de la altitud) tipo. Robert von Sterneck (1883, resultados entre 5.0 y 6.3 g/cm) aún continuaron realizando experimentos de péndulo. >3) y Thomas Corwin Mendenhall (1880, 5,77 g/cm³).

El resultado de Cavendish fue mejorado por primera vez por John Henry Poynting (1891), quien publicó un valor de 5,49(3) g·cm⁻³, que difiere del valor moderno en un 0,2 %, pero es compatible con el valor moderno dentro de la incertidumbre estándar citada del 0,55 %. Además de Poynting, C. V. Boys (1895) y Carl Braun (1897) realizaron mediciones, con resultados compatibles que sugieren $G$ = 6.66(1)×10⁻¹¹ m³⋅kg⁻¹⋅s⁻². La notación moderna que involucra la constante $G$ fue introducida por Boys en 1894 y se convirtió en estándar a fines de la década de 1890, con valores que generalmente se citan en el sistema cgs. Richarz y Krigar-Menzel (1898) intentaron repetir el experimento de Cavendish utilizando 100 000 kg de plomo como masa atrayente. La precisión de su resultado de 6.683(11)×10⁻¹¹ m³⋅kg⁻¹⋅s⁻² fue, sin embargo, del mismo orden de magnitud que los otros resultados en ese momento.

Arthur Stanley Mackenzie en Las leyes de la gravitación (1899) repasa el trabajo realizado en el siglo XIX. Poynting es el autor del artículo "Gravitation" en la Encyclopædia Britannica undécima edición (1911). Aquí, cita un valor de $G$ = 6,66×10⁻¹¹ m³⋅ kg⁻¹⋅s⁻² con una incertidumbre del 0,2 %.

Valor moderno

Paul R. Heyl (1930) publicó el valor de 6,670(5)×10⁻¹¹ m³⋅kg⁻¹⋅ s⁻² (incertidumbre relativa 0,1 %), mejorado a 6,673(3)×10⁻¹¹ m³⋅kg⁻¹⋅s⁻² (incertidumbre relativa 0,045 % = 450 ppm) en 1942.

Los valores publicados de $G$ derivados de mediciones de alta precisión desde la década de 1950 siguen siendo compatibles con Heyl (1930), pero dentro de la incertidumbre relativa de alrededor del 0,1% (o 1000 ppm) ha variado bastante, y no está del todo claro si la incertidumbre se ha reducido en absoluto desde la medición de 1942. Algunas medidas publicadas en las décadas de 1980 a 2000 eran, de hecho, mutuamente excluyentes. Por lo tanto, establecer un valor estándar para $G$ con una incertidumbre estándar superior al 0,1 % sigue siendo bastante especulativo.

En 1969, el valor recomendado por el Instituto Nacional de Estándares y Tecnología (NIST) se citó con una incertidumbre estándar de 0,046 % (460 ppm), que se redujo a 0,012 % (120 ppm) en 1986. Pero la publicación continua de las mediciones contradictorias llevaron al NIST a aumentar considerablemente la incertidumbre estándar en el valor recomendado de 1998, por un factor de 12, a una incertidumbre estándar de 0,15 %, mayor que la dada por Heyl (1930).

La incertidumbre se redujo nuevamente en 2002 y 2006, pero se elevó nuevamente, en un 20 % más conservador, en 2010, igualando la incertidumbre estándar de 120 ppm publicada en 1986. Para la actualización de 2014, CODATA redujo la incertidumbre a 46 ppm, menos de la mitad del valor de 2010 y un orden de magnitud por debajo de la recomendación de 1969.

La siguiente tabla muestra los valores recomendados por NIST publicados desde 1969:

Timeline of measurements and recommended values for G desde 1900: los valores recomendados basados en una revisión bibliográfica se muestran en experimentos de balance de torsión en azul, otros tipos de experimentos en verde.

Valores recomendados para G
Año	G (10)^{−11 -}·m³⋅kg⁻¹⋅s⁻²)	Normativa de incertidumbre
1969	6.6732(31)	460 ppm
1973	6.6720(49)	730 ppm
1986	6.67449(81)	120 ppm
1998	6.673(10)	1.500 ppm
2002	6.6742(10)	150 ppm
2006	6.67428(67)	100 ppm
2010	6.67384(80)	120 ppm
2014	6.67408(31)	46 ppm
2018	6.67430(15)	22 ppm

En la edición de enero de 2007 de Science, Fixler et al. describió una medición de la constante gravitatoria mediante una nueva técnica, la interferometría atómica, informando un valor de $G$ = 6.693(34)×10⁻¹¹ m³⋅kg⁻¹⋅s⁻², 0,28 % (2800 ppm) superior al valor CODATA de 2006. Una medición mejorada de átomos fríos por Rosi et al. fue publicado en 2014 de $G$ = 6,67191(99)×10⁻¹¹ m³⋅kg⁻¹⋅s⁻². Aunque mucho más cercano al valor aceptado (lo que sugiere que la medición de Fixler et al. fue errónea), este resultado fue 325 ppm por debajo del valor recomendado de CODATA de 2014, con intervalos de incertidumbre estándar que no se superponen.

A partir de 2018, se están realizando esfuerzos para reevaluar los resultados contradictorios de las mediciones, coordinados por el NIST, en particular, una repetición de los experimentos informados por Quinn et al. (2013).

En agosto de 2018, un grupo de investigación chino anunció nuevas mediciones basadas en balanzas de torsión, 6,674184(78)×10⁻¹¹ m³⋅kg⁻¹⋅s⁻² y 6,674484(78)×10⁻¹¹ m³⋅kg⁻¹⋅s⁻² basado en dos métodos diferentes. Estas se afirman como las mediciones más precisas jamás realizadas, con incertidumbres estándar citadas tan bajas como 12 ppm. La diferencia de 2,7σ entre los dos resultados sugiere que podría haber fuentes de error no explicadas.

Variación de tiempo sugerida

Un controvertido estudio de 2015 de algunas mediciones anteriores de $G$ , realizado por Anderson et al., sugirió que la mayoría de los valores mutuamente excluyentes en las mediciones de precisión de G pueden explicarse por una variación periódica. La variación se midió con un período de 5,9 años, similar al observado en las mediciones de la duración del día (LOD), lo que sugiere una causa física común que no es necesariamente una variación en $G$ . Algunos de los autores originales de las mediciones de $G$ utilizadas en Anderson et al. Esta respuesta señala que Anderson et al. no solo omitieron mediciones, sino que también utilizaron el momento de la publicación en lugar del momento en que se realizaron los experimentos. Una gráfica con el tiempo estimado de medición a partir del contacto con los autores originales degrada seriamente la correlación de la duración del día. Además, la consideración de los datos recopilados durante una década por Karagioz e Izmailov no muestra correlación con las mediciones de la duración del día. Como tal, las variaciones en $G$ probablemente se deban a errores de medición sistemáticos que no se han tenido en cuenta correctamente. Bajo el supuesto de que la física de las supernovas de tipo Ia es universal, el análisis de las observaciones de 580 de ellas ha demostrado que la constante gravitatoria ha variado menos de una parte en diez mil millones por año durante los últimos nueve mil millones de años según Mold et al. (2014).

Contenido relacionado

Más resultados...