Conservación de la masa

La reacción de combustión del metano. Donde 4 átomos de hidrógeno, 4 átomos de oxígeno y 1 de carbono están presentes antes y después de la reacción. La masa total después de la reacción es la misma que antes de la reacción.

En física y química, la ley de conservación de la masa o principio de conservación de la masa establece que para cualquier sistema cerrado a todas las transferencias de materia y energía, la masa de el sistema debe permanecer constante en el tiempo, ya que la masa del sistema no puede cambiar, por lo que la cantidad no se puede agregar ni quitar. Por lo tanto, la cantidad de masa se conserva en el tiempo.

La ley implica que la masa no se puede crear ni destruir, aunque se puede reorganizar en el espacio, o las entidades asociadas a ella pueden cambiar de forma. Por ejemplo, en las reacciones químicas, la masa de los componentes químicos antes de la reacción es igual a la masa de los componentes después de la reacción. Así, durante cualquier reacción química y proceso termodinámico de baja energía en un sistema aislado, la masa total de los reactivos o materiales de partida debe ser igual a la masa de los productos.

El concepto de conservación de la masa se usa ampliamente en muchos campos, como la química, la mecánica y la dinámica de fluidos. Históricamente, la conservación de la masa en las reacciones químicas fue demostrada principalmente por Jean Rey (en 1630) y luego redescubierta por Antoine Lavoisier a fines del siglo XVIII. La formulación de esta ley fue de crucial importancia en el progreso de la alquimia a la moderna ciencia natural de la química.

En realidad, la conservación de la masa solo es válida aproximadamente y se considera parte de una serie de suposiciones en la mecánica clásica. La ley debe modificarse para cumplir con las leyes de la mecánica cuántica y la relatividad especial bajo el principio de equivalencia masa-energía, que establece que la energía y la masa forman una cantidad conservada. Para sistemas muy energéticos, se demuestra que la conservación de la masa no se cumple, como es el caso de las reacciones nucleares y la aniquilación de partículas-antipartículas en la física de partículas.

La masa tampoco se conserva generalmente en los sistemas abiertos. Tal es el caso cuando se permiten varias formas de energía y materia dentro o fuera del sistema. Sin embargo, a menos que estén involucradas la radiactividad o las reacciones nucleares, la cantidad de energía que escapa (o ingresa) a sistemas como el calor, el trabajo mecánico o la radiación electromagnética generalmente es demasiado pequeña para medirse como una disminución (o aumento) en la masa del sistema..

Para los sistemas que incluyen grandes campos gravitatorios, se debe tener en cuenta la relatividad general; así, la conservación de masa-energía se convierte en un concepto más complejo, sujeto a diferentes definiciones, y ni la masa ni la energía se conservan tan estricta y simplemente como en el caso de la relatividad especial.

Formulación y ejemplos

La ley de conservación de masa sólo puede ser formulada en la mecánica clásica, en la que las escalas energéticas asociadas con un sistema aislado son mucho más pequeñas que las mc2{displaystyle mc^{2}, donde m{displaystyle m} es la masa de un objeto típico en el sistema, medido en el marco de referencia donde el objeto está en reposo, y c{displaystyle c} es la velocidad de la luz.

La ley se puede formular matemáticamente en los campos de la mecánica de fluidos y la mecánica de medios continuos, donde la conservación de la masa se suele expresar mediante la ecuación de continuidad, dada en forma diferencial como

∂ ∂ *** *** ∂ ∂ t+Silencio Silencio ⋅ ⋅ ()*** *** v)=0,{displaystyle {frac {partial rho }{partial t}}+nabla cdot (rho mathbf {v})=0,}

*** *** {textstyle rho }

t{textstyle t}

Silencio Silencio ⋅ ⋅ {textstyle nabla cdot }

v{textstyle mathbf {v}

La interpretación de la ecuación de continuidad para la masa es la siguiente: Para una superficie cerrada dada en el sistema, el cambio, en cualquier intervalo de tiempo, de la masa encerrada por la superficie es igual a la masa que atraviesa la superficie durante ese intervalo de tiempo: positivo si el asunto entra y negativo si el asunto sale. Para todo el sistema aislado, esta condición implica que la masa total M{textstyle M}, la suma de las masas de todos los componentes del sistema, no cambia con el tiempo, es decir.

dMdt=ddt∫ ∫ *** *** dV=0,{displaystyle {frac {text{d}M} {text{d}t}={frac} {f}}}} {f}} {text{d}{text{d}t}int rho ,{text{d}V=0,}

dV{textstyle {text{d}V}

La ecuación de continuidad de la masa forma parte de las ecuaciones de Euler de la dinámica de fluidos. Muchas otras ecuaciones de convección-difusión describen la conservación y el flujo de masa y materia en un sistema dado.

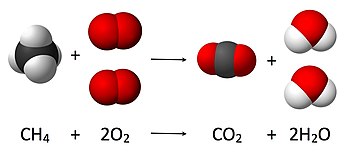
En química, el cálculo de la cantidad de reactivos y productos en una reacción química, o estequiometría, se basa en el principio de conservación de la masa. El principio implica que durante una reacción química la masa total de los reactivos es igual a la masa total de los productos. Por ejemplo, en la siguiente reacción

donde una molécula de metano (CH
₄) y dos moléculas de oxígeno O
₂ se convierten en una molécula de dióxido de carbono (CO
₂) y dos de agua (H
₂O). El número de moléculas resultantes de la reacción se puede derivar del principio de conservación de la masa, ya que inicialmente están presentes cuatro átomos de hidrógeno, 4 átomos de oxígeno y un átomo de carbono (así como en el estado final); por tanto, el número de moléculas de agua producidas debe ser exactamente dos por molécula de dióxido de carbono producida.

Muchos problemas de ingeniería se resuelven siguiendo la distribución de masa de un sistema determinado a lo largo del tiempo; esta metodología se conoce como balance de masa.

Historia

El científico ruso Mikhail Lomonosov formuló la ley de conservación de masas en 1756 y llegó a la conclusión de que la teoría de la flogista es incorrecta.

El descubrimiento de Antoine Lavoisier de la ley de conservación de masas llevó a muchos nuevos hallazgos en el siglo XIX. La ley de Joseph Proust de proporciones definidas y la teoría atómica de John Dalton se ramificaron de los descubrimientos de Antoine Lavoisier. Los experimentos cuantitativos de Lavoisier revelaron que la combustión involucró oxígeno en lugar de lo que se pensaba anteriormente como flogistón.

Ya en el año 520 a. C., la filosofía jainista, una filosofía no creacionista basada en las enseñanzas de Mahavira, afirmó que el universo y sus componentes, como la materia, no se pueden destruir ni crear. El texto jainista Tattvarthasutra (siglo II d. C.) establece que una sustancia es permanente, pero sus modos se caracterizan por la creación y la destrucción.

Una idea importante en la filosofía griega antigua era que "Nada proviene de la nada", por lo que lo que existe ahora siempre ha existido: ninguna materia nueva puede surgir donde antes no existía. Una declaración explícita de esto, junto con el principio adicional de que nada puede convertirse en nada, se encuentra en Empédocles (c. siglo IV a. C.): "Porque es imposible que cualquier cosa venga de lo que no es, y no se puede producir ni oír hablar de que lo que es debe ser completamente destruido."

Epicuro estableció otro principio de conservación alrededor del siglo III a. C., quien escribió al describir la naturaleza del Universo que "la totalidad de las cosas siempre fue tal como es ahora y siempre será".;.

Descubrimientos en química

En el siglo XVIII, el principio de conservación de la masa durante las reacciones químicas se usaba ampliamente y era una suposición importante durante los experimentos, incluso antes de que se estableciera formalmente una definición, como se puede ver en los trabajos de Joseph Black, Henry Cavendish y Jean Rey. El primero en delinear el principio fue Mikhail Lomonosov en 1756. Es posible que lo haya demostrado mediante experimentos y ciertamente discutió el principio en 1748 en correspondencia con Leonhard Euler, aunque a veces se cuestiona su afirmación sobre el tema. Según el físico soviético Yakov Dorfman:

La ley universal fue formulada por Lomonosov sobre la base de consideraciones materialistas filosóficas generales, nunca fue cuestionada o probada por él, pero por el contrario, lo servía como una sólida posición de partida en toda investigación a lo largo de su vida.

Más tarde, Antoine Lavoisier llevó a cabo una serie de experimentos más refinados, quien expresó su conclusión en 1773 y popularizó el principio de conservación de la masa. Las demostraciones del principio desmintieron la entonces popular teoría del flogisto que decía que se podía ganar o perder masa en los procesos de combustión y calor.

La conservación de la masa fue oscura durante milenios debido al efecto de flotabilidad de la atmósfera terrestre sobre el peso de los gases. Por ejemplo, un trozo de madera pesa menos después de quemarlo; esto parecía sugerir que parte de su masa desaparece, o se transforma o se pierde. Esto no fue refutado hasta que se llevaron a cabo cuidadosos experimentos en los que se permitió que tuvieran lugar reacciones químicas como la oxidación en ampollas de vidrio selladas; se encontró que la reacción química no cambió el peso del recipiente sellado y su contenido. El pesaje de gases mediante balanzas no fue posible hasta la invención de la bomba de vacío en el siglo XVII.

Una vez comprendida, la conservación de la masa fue de gran importancia en el progreso de la alquimia a la química moderna. Una vez que los primeros químicos se dieron cuenta de que las sustancias químicas nunca desaparecían sino que solo se transformaban en otras sustancias con el mismo peso, estos científicos pudieron por primera vez embarcarse en estudios cuantitativos de las transformaciones de las sustancias. La idea de la conservación de la masa más la suposición de que ciertas "sustancias elementales" tampoco podían transformarse en otros mediante reacciones químicas, lo que a su vez condujo a la comprensión de los elementos químicos, así como a la idea de que todos los procesos y transformaciones químicos (como las reacciones metabólicas y de combustión) son reacciones entre cantidades o pesos invariantes de estos elementos químicos. elementos.

Siguiendo el trabajo pionero de Lavoisier, los exhaustivos experimentos de Jean Stas avalaron la consistencia de esta ley en las reacciones químicas, aunque se llevaron a cabo con otras intenciones. Su investigación indicó que en ciertas reacciones la pérdida o ganancia no podría haber sido más de 2 a 4 partes en 100.000. La diferencia en la precisión buscada y alcanzada por Lavoisier por un lado, y por Morley y Stas por el otro, es enorme.

Física moderna

La ley de conservación de la masa fue desafiada con el advenimiento de la relatividad especial. En uno de los artículos Annus Mirabilis de Albert Einstein en 1905, sugirió una equivalencia entre masa y energía. Esta teoría implicaba varias afirmaciones, como la idea de que la energía interna de un sistema podría contribuir a la masa de todo el sistema, o que la masa podría convertirse en radiación electromagnética. Sin embargo, como señaló Max Planck, un cambio de masa como resultado de la extracción o adición de energía química, como lo predice la teoría de Einstein, es tan pequeño que no se puede medir con los instrumentos disponibles y no se puede medir. presentado como una prueba de relatividad especial. Einstein especuló que las energías asociadas con la radiactividad recién descubierta eran lo suficientemente significativas, en comparación con la masa de los sistemas que las producían, para permitir medir su cambio de masa, una vez que la energía de la reacción había sido eliminada del sistema. De hecho, esto más tarde demostró ser posible, aunque eventualmente sería la primera reacción de transmutación nuclear artificial en 1932, demostrada por Cockcroft y Walton, que resultó ser la primera prueba exitosa de la teoría de Einstein sobre la pérdida de masa con ganancia de energía.

La ley de conservación de la masa y la ley análoga de conservación de la energía se generalizaron y unificaron finalmente en el principio de equivalencia masiva y energética, descrito por la famosa fórmula de Albert EinsteinE=mc2{displaystyle E=mc^{2}. La relatividad especial también redefine el concepto de masa y energía, que se puede utilizar intercambiablemente y se definen en relación con el marco de referencia. Había que definir varias cantidades para la consistencia, como las masa de descanso de una partícula (masa en el marco de reposo de la partícula) y la masa relativista (en otro marco). Este último término suele utilizarse con menos frecuencia.

Generalización

Relatividad especial

En relatividad especial, la conservación de la masa no se aplica si el sistema está abierto y la energía se escapa. Sin embargo, continúa aplicándose a sistemas totalmente cerrados (aislados). Si la energía no puede escapar de un sistema, su masa no puede disminuir. En la teoría de la relatividad, siempre que se retenga cualquier tipo de energía dentro de un sistema, esta energía exhibe masa.

Además, la masa debe diferenciarse de la materia, ya que la materia puede no estar perfectamente conservada en sistemas aislados, aunque la masa siempre se conserva en dichos sistemas. Sin embargo, la materia está tan casi conservada en química que las violaciones de la conservación de la materia no se midieron hasta la era nuclear, y la suposición de la conservación de la materia sigue siendo un concepto práctico importante en la mayoría de los sistemas en química y otros estudios que no involucran las altas energías típicas de radiactividad y reacciones nucleares.

La masa asociada con cantidades químicas de energía es demasiado pequeña para medirla

El cambio en la masa de ciertos tipos de sistemas abiertos donde los átomos o partículas masivas no pueden escapar, pero otros tipos de energía (como la luz o el calor) sí pueden entrar, escapar o fusionarse, pasó desapercibido durante el XIX, porque el cambio de masa asociado con la adición o pérdida de pequeñas cantidades de energía térmica o radiante en las reacciones químicas es muy pequeño. (En teoría, la masa no cambiaría en absoluto para los experimentos realizados en sistemas aislados donde no se permitía la entrada o salida de calor y trabajo).

La conservación de masa sigue siendo correcta si no se pierde energía

La conservación de la masa relativista implica el punto de vista de un solo observador (o la vista desde un solo marco inercial) ya que cambiar los marcos inerciales puede resultar en un cambio de la energía total (energía relativista) para los sistemas, y esta cantidad determina la masa relativista.

El principio de que la masa de un sistema de partículas debe ser igual a la suma de sus masas en reposo, aunque sea cierto en la física clásica, puede ser falso en la relatividad especial. La razón por la que las masas en reposo no se pueden simplemente sumar es que esto no tiene en cuenta otras formas de energía, como la energía cinética y potencial, y las partículas sin masa como los fotones, todas las cuales pueden (o no) afectar la masa total de sistemas

Para mover partículas masivas en un sistema, examinar las masas en reposo de las diversas partículas también equivale a introducir muchos marcos de observación inercial diferentes (lo cual está prohibido si se quiere conservar la energía y el momento totales del sistema), y también cuando en el resto marco de una partícula, este procedimiento ignora los momentos de otras partículas, que afectan la masa del sistema si las otras partículas están en movimiento en este marco.

Para el tipo especial de masa llamada masa invariante, cambiar el marco de observación inercial para un sistema cerrado completo no tiene efecto en la medida de la masa invariante del sistema, que permanece tanto conservada como invariante (invariable), incluso para diferentes observadores que ven todo el sistema. La masa invariante es una combinación de sistema de energía y cantidad de movimiento, que es invariable para cualquier observador, porque en cualquier sistema de inercia, las energías y las cantidades de movimiento de las diversas partículas siempre suman la misma cantidad (la cantidad de movimiento puede ser negativa, por lo que la suma equivale a una resta). La masa invariante es la masa relativista del sistema cuando se ve en el marco del centro del momento. Es la masa mínima que puede exhibir un sistema, visto desde todos los marcos inerciales posibles.

La conservación de la masa tanto relativista como invariante se aplica incluso a sistemas de partículas creados por producción de pares, donde la energía para nuevas partículas puede provenir de la energía cinética de otras partículas, o de uno o más fotones como parte de un sistema que incluye otras partículas además de un fotón. De nuevo, ni la masa relativista ni la invariante de los sistemas totalmente cerrados (es decir, aislados) cambian cuando se crean nuevas partículas. Sin embargo, diferentes observadores inerciales estarán en desacuerdo sobre el valor de esta masa conservada, si es la masa relativista (es decir, la masa relativista se conserva pero no es invariante). Sin embargo, todos los observadores están de acuerdo en el valor de la masa conservada si la masa que se mide es la masa invariante (es decir, la masa invariante es conservada e invariante).

La fórmula de equivalencia de energía masiva da una predicción diferente en sistemas no aislados, ya que si se permite la energía escapar de un sistema, tanto la masa relativista como la masa invariante escaparán también. En este caso, la fórmula de equivalencia de energía masiva predice que la cambio en masa de un sistema se asocia con el cambio en su energía debido a la energía añadida o restringida: Δ Δ m=Δ Δ E/c2.{displaystyle Delta m=Delta E/c^{2}.} Esta forma de cambios fue la forma en la que esta famosa ecuación fue presentada originalmente por Einstein. En este sentido, los cambios masivos en cualquier sistema se explican simplemente si se tiene en cuenta la masa de la energía agregada o eliminada del sistema.

La fórmula implica que los sistemas ligados tienen una masa invariable (masa en reposo para el sistema) menor que la suma de sus partes, si se ha permitido que la energía de ligadura escape del sistema después de que el sistema se haya ligado. Esto puede suceder al convertir la energía potencial del sistema en algún otro tipo de energía activa, como energía cinética o fotones, que escapan fácilmente de un sistema ligado. La diferencia en las masas del sistema, llamada defecto de masa, es una medida de la energía de enlace en los sistemas enlazados; en otras palabras, la energía necesaria para romper el sistema. Cuanto mayor sea el defecto de masa, mayor será la energía de enlace. La energía de enlace (que en sí misma tiene masa) debe liberarse (como luz o calor) cuando las partes se combinan para formar el sistema de enlace, y esta es la razón por la que la masa del sistema de enlace disminuye cuando la energía abandona el sistema. La masa invariante total se conserva realmente cuando se tiene en cuenta la masa de la energía de enlace que se ha escapado.

Relatividad general

En relatividad general, la masa invariante total de fotones en un volumen de espacio en expansión disminuirá debido al corrimiento hacia el rojo de dicha expansión. Por lo tanto, la conservación tanto de la masa como de la energía depende de varias correcciones hechas a la energía en la teoría, debido a la energía potencial gravitatoria cambiante de tales sistemas.