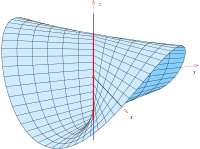
Conoide

En geometría, un conoide (del griego κωνος, 'cono' y ειδης, 'similar') es una superficie reglada, cuyas líneas cumplen las condiciones adicionales:

1) Todas las decisiones son paralelas a un plano, el avión directo.

2) Todos los fallos intersectan una línea fija, la axis.

El conoide es recto si su eje es perpendicular a su plano directriz. Por lo tanto, todas las líneas son perpendiculares al eje.

Debido a que (1) cualquier conoide es una superficie catalana y puede representarse paramétricamente por

${\displaystyle \mathbf {x} (u,v)=\mathbf {c} (u)+v\mathbf {r} (u)\ }$

Cualquier curva x(u₀,v) con parámetro fijo u = u₀ es una curva rectora, c(u) describe la directriz y los vectores r(u) son todos paralelos al plano directriz. La planaridad de los vectores r(u) se puede representar por

${\displaystyle \det(\mathbf {r}\mathbf {\ dot {}\mathbf {\ddot {}}=0}$.

Si la directriz es un círculo, el conoide se llama conoide circular.

El término conoide ya fue utilizado por Arquímedes en su tratado Sobre los conoides y los esferoides.

La representación paramétrica

${\displaystyle \mathbf {x} (u,v)=(\cos u,\sin u,0)+v(0,-\sin u,z_{0})\ 0\leq u won2\piv\in \mathbb {R}$

describe un conoide circular derecho con el círculo de unidad del x-y-plane como directrix y un plano directo, que es paralelo al y-z-plane. Su eje es la línea ${\displaystyle (x,0,z_{0})\ x\in \mathbb {R} \.}$

Características especiales:

1. La intersección con un plano horizontal es una elipse.
2. ${\displaystyle (1-x^{2}(z-z_{0})}-y^{2}z_{0}{2}=0}$ es una representación implícita. Por lo tanto el conoide circular derecho es una superficie del grado 4.
3. La regla de Kepler da para un conoide circular derecho con radio ${\displaystyle r}$ y altura ${\displaystyle h}$ el volumen exacto: ${\displaystyle V={\tfrac {\\fnMicrosoft {\\fnMicrosoft {\\\fnMicrosoft {\\\fnMicrosoft {\\\\\fnMicrosoft {\fnMicrosoft {\fnMicrosoft {\\fnMicrosoft {\\fnMicrosoft {\\\fnMicrosoft {\\\\\\\fnMicrosoft {\\\\\\\\\\fnMicrosoft {\fnMicrosoft {\fnMicrosoft {\\\\\fnMicrosoft {\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\fnMicrosoft {\fnMicrosoft {\fnMicrosoft {\fnMicrosoft {\fnMicrosoft {\\\\\\\\\\\\\\\\\\\fnMicrosoft {\\fnMicro } {2}r^{2}h}$.

La representación implícita se cumple por los puntos de la línea ${\displaystyle (x,0,z_{0})}$, también. Para estos puntos no existen aviones tangentes. Tales puntos se llaman singular.

La representación paramétrica

${\displaystyle \mathbf {x} (u,v)=\left(1,u,-u^{2}\right)+v\left(-1,0,u^{2}\right)}$

${\displaystyle =\left(1-v,u,-(1-v)u^{2}\right)\u,v\in \mathbb {R} \ ~$

describe a parabólica conoid con la ecuación ${\displaystyle z=-xy^{2}$. El conoide tiene una parabola como directrix, el eje y como eje y un plano paralelo al plano x-z como plano directo. Es utilizado por arquitectos como superficie de techo (s. abajo).

El conoide parabólico no tiene puntos singulares.

1. paraboloide hiperbólico
2. Plücker conoid
3. Whitney Umbrella
4. helicoid

• 
  paraboloide hiperbólico
• 
  Plücker conoid
• 
  Paraguas Whitney

Existen muchos conoides con puntos singulares que se estudian en geometría algebraica.

Al igual que otras superficies regladas, los conoides son de gran interés para los arquitectos, ya que se pueden construir utilizando vigas o barras. Los conoides rectos se pueden fabricar fácilmente: se colocan barras sobre un eje de manera que puedan rotar únicamente alrededor de este eje. Después, se desvían las barras mediante una directriz y se genera un conoide (es decir, un conoide parabólico).

• mathworld: Plücker conoid
• "Conoide", Enciclopedia de Matemáticas, EMS Press, 2001 [1994]

• A. Gray, E. Abbena, S. Salamon, Geometría diferencial moderna de curvas y superficies con Mathematica, 3a edición. Boca Raton, FL:CRC Press, 2006. [1] (ISBN 978-1-58488-448-4)
• Vladimir Y. Rovenskii, Geometría de curvas y superficies con MAPLE [2] (ISBN 978-0-8176-4074-3)