Conjunto parcialmente pedido
| Relaciones binarias transitivas | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

En matemáticas, especialmente en teoría del orden, un conjunto parcialmente ordenado (también poset) formaliza y generaliza el concepto intuitivo de una ordenación, secuencia o disposición de los elementos de un conjunto. Un poset consiste en un conjunto junto con una relación binaria que indica que, para ciertos pares de elementos del conjunto, uno de los elementos precede al otro en el orden. La relación en sí se denomina "orden parcial".
La palabra parcial en los nombres "orden parcial" y "conjunto parcialmente ordenado" se utiliza como una indicación de que no todos los pares de elementos deben ser comparables. Es decir, puede haber pares de elementos para los cuales ninguno de los elementos precede al otro en la poset. Los pedidos parciales generalizan así los pedidos totales, en los que cada par es comparable.
Definición informal
Un orden parcial define una noción de comparación. Dos elementos x e y pueden estar en cualquiera de las cuatro relaciones mutuamente excluyentes entre sí: x < y, o x = y, o x > y, o x e y son incomparables.
Un conjunto con un orden parcial se llama conjunto parcialmente ordenado (también llamado poset). El término conjunto ordenado también se usa a veces, siempre que quede claro por el contexto que no se refiere a ningún otro tipo de orden. En particular, los conjuntos totalmente ordenados también pueden denominarse "conjuntos ordenados", especialmente en áreas donde estas estructuras son más comunes que los posets.
Un poset se puede visualizar a través de su diagrama de Hasse, que representa la relación de orden.
Relación de orden parcial
Una relación de orden parcial es una relación homogénea que es transitiva y antisimétrica. Hay dos subdefiniciones comunes para una relación de orden parcial, para relaciones de orden parcial reflexivas e irreflexivas, también llamadas "no estrictas" y "estricto" respectivamente. Las dos definiciones se pueden poner en una correspondencia uno a uno, por lo que para cada orden parcial estricto hay un único orden parcial no estricto correspondiente, y viceversa. El término orden parcial normalmente se refiere a una relación de orden parcial no estricta.
Orden parcial no estricto
A reflexivo, débil, o Orden parcial no restrictivo es una relación homogénea ≤ en un conjunto P{displaystyle P} que es reflexivo, antisimétrico y transitivo. Eso es, para todos a,b,c▪ ▪ P,{displaystyle a,b,cin P,} debe satisfacer:
- Reflexividad: a≤ ≤ a{displaystyle aleq a}, es decir, cada elemento está relacionado con sí mismo.
- Antisimetría: si a≤ ≤ b{displaystyle aleq b} y b≤ ≤ a{displaystyle bleq a} entonces a=b{displaystyle a=b}, es decir, no se preceden dos elementos distintos.
- Transitividad: si a≤ ≤ b{displaystyle aleq b} y b≤ ≤ c{displaystyle bleq c} entonces a≤ ≤ c{displaystyle aleq c}.
Un orden parcial no estricto también se conoce como preorden antisimétrico.
Orden parcial estricto
An irreflexivo, fuerte, o estricto orden parcial es una relación homogénea P{displaystyle P} que es irreflexivo, asimétrico y transitivo; es decir, satisface las siguientes condiciones para todos a,b,c▪ ▪ P:{displaystyle a,b,cin P:}
- Irreflexividad: no <math alttext="{displaystyle aa.a{displaystyle a wona}<img alt="{displaystyle a, es decir, ningún elemento está relacionado con sí mismo (también llamado antirreflexivo).
- Asimetría: si <math alttext="{displaystyle aa.b{displaystyle a meantb}<img alt="a entonces no <math alttext="{displaystyle bb.a{displaystyle b madea}<img alt="b .
- Transitividad: si <math alttext="{displaystyle aa.b{displaystyle a meantb}<img alt="a y <math alttext="{displaystyle bb.c{displaystyle b)<img alt="b entonces <math alttext="{displaystyle aa.c{displaystyle aludec}<img alt="a .
Irreflexividad y transitividad juntas implican asimetría. Además, la asimetría implica irreflexividad. En otras palabras, una relación transitiva es asimétrica si y solo si es irreflexiva. Entonces, la definición es la misma si omite la irreflexividad o la asimetría (pero no ambas).
Un pedido parcial estricto también se conoce como pedido anticipado estricto.
Correspondencia de relaciones de orden parcial estricto y no estricto
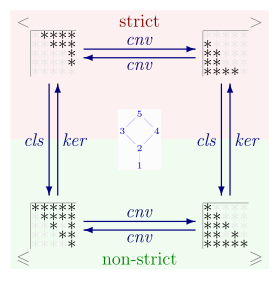
Órdenes parciales estrictas y no limitadas en un conjunto P{displaystyle P} están estrechamente relacionados. Una orden parcial no restrictiva ≤ ≤ {displaystyle leq } puede ser convertido a un orden parcial estricto eliminando todas las relaciones de la forma a≤ ≤ a;{displaystyle aleq a;} es decir, el estricto orden parcial es el conjunto <math alttext="{displaystyle .:=≤ ≤ ∖ ∖ Δ Δ P{displaystyle >:=leq setminus Delta ¿Qué?<img alt="{displaystyle Donde Δ Δ P:={}()p,p):p▪ ▪ P}{displaystyle Delta ¿Qué? es la relación de identidad P× × P{displaystyle Ptimes P} y ∖ ∖ {displaystyle ;setminus ;} denota la resta. Por el contrario, una orden parcial estricta P{displaystyle P} puede ser convertido a un orden parcial no-stricto al unir todas las relaciones de esa forma; es decir, <math alttext="{displaystyle leq ;:=;Delta _{P};cup ;≤ ≤ :=Δ Δ P∪ ∪ .{displaystyle leq ;:=;Delta _{P};cup ;<img alt="{displaystyle leq ;:=;Delta _{P};cup ; es un orden parcial no restringido. Así, si ≤ ≤ {displaystyle leq } es un orden parcial no-stricto, entonces el orden parcial estricto correspondiente es el núcleo irreflexivo dado por
Pedidos dobles
El dual (o opuesto) Roperaciones{displaystyle R^{text{op}} de una relación de orden parcial R{displaystyle R. se define por dejar Roperaciones{displaystyle R^{text{op}} ser la relación conversa R{displaystyle R., es decir. xRoperacionesSí.{displaystyle - Sí. si Sí.Rx{displaystyle yRx}. El doble de un orden parcial no-stricto es un orden parcial no-stricto, y el doble de un orden parcial estricto es un orden parcial estricto. El doble de una relación dual es la relación original.
Notación
Podemos considerar una pose como un 3-tuple <math alttext="{displaystyle (P,leq()P,≤ ≤ ,.){displaystyle (P,leqse)}<img alt="{displaystyle (P,leq, donde ≤ ≤ {displaystyle leq } es una relación de orden parcial no restringido P{displaystyle P}, <math alttext="{displaystyle .{displaystyle]<img alt=" es la relación estricta del orden parcial asociado P{displaystyle P} (el núcleo irreflexivo de ≤ ≤ {displaystyle leq }), ≥ ≥ {displaystyle geq } es el doble ≤ ≤ {displaystyle leq }, y }" xmlns="http://www.w3.org/1998/Math/MathML">■{displaystyle } " aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/1b27b77ab4e3293ea9ce65cef60fea655c398423" style="vertical-align: -0.338ex; width:1.808ex; height:1.843ex;"/> es el doble <math alttext="{displaystyle .{displaystyle]<img alt=".
Cualquiera de las cuatro relaciones de orden parcial <math alttext="{displaystyle leq}" xmlns="http://www.w3.org/1998/Math/MathML">≤ ≤ ,.,≥ ≥ ,y■{displaystyle leq made,geq{text{ and }}}}}}<img alt="{displaystyle leq}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/22333493c1c1bdfdd07babc8d8392833d065d5d4" style="vertical-align: -0.671ex; width:15.888ex; height:2.509ex;"/> en un determinado conjunto determina únicamente los otros tres. Por lo tanto, como cuestión de notación, se puede escribir ()P,≤ ≤ ){displaystyle (P,leq)} o <math alttext="{displaystyle (P,()P,.){displaystyle (P, interpretado)}<img alt="{displaystyle (P,, y asumir que las otras relaciones se definen apropiadamente. Definición mediante una orden parcial no restrictiva ≤ ≤ {displaystyle leq } es más común. Algunos autores usan símbolos diferentes que otros ≤ ≤ {displaystyle leq } tales como ⊑ ⊑ {displaystyle sqsubseteq } o ⪯ ⪯ {displaystyle preceq } para distinguir las órdenes parciales de las órdenes totales.
Cuando se refiere a órdenes parciales, ≤ ≤ {displaystyle leq } no debe tomarse como complemento }" xmlns="http://www.w3.org/1998/Math/MathML">■{displaystyle } " aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/1b27b77ab4e3293ea9ce65cef60fea655c398423" style="vertical-align: -0.338ex; width:1.808ex; height:1.843ex;"/>. La relación }" xmlns="http://www.w3.org/1998/Math/MathML">■{displaystyle }
" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/1b27b77ab4e3293ea9ce65cef60fea655c398423" style="vertical-align: -0.338ex; width:1.808ex; height:1.843ex;"/> es el contrario del núcleo irreflexivo ≤ ≤ {displaystyle leq }, que es siempre un subconjunto del complemento de ≤ ≤ {displaystyle leq }, pero }" xmlns="http://www.w3.org/1998/Math/MathML">■{displaystyle }
" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/1b27b77ab4e3293ea9ce65cef60fea655c398423" style="vertical-align: -0.338ex; width:1.808ex; height:1.843ex;"/> es igual al complemento ≤ ≤ {displaystyle leq } si, y sólo si, ≤ ≤ {displaystyle leq } es un orden total.
Ejemplos
Los ejemplos estándar de posets que surgen en matemáticas incluyen:
- Los números reales, o en general cualquier conjunto totalmente ordenado, ordenado por el estándar menos que igual relación ≤, es un orden parcial no-stricto.
- En números reales R{displaystyle mathbb {R}, lo habitual menos que relación < es un orden parcial estricto. Lo mismo también es cierto de lo habitual más grande que relación R{displaystyle mathbb {R}.
- Por definición, todo orden débil estricto es un orden parcial estricto.
- El conjunto de subconjuntos de un determinado conjunto (su conjunto de potencia) ordenado por la inclusión (véase Fig.1). Del mismo modo, el conjunto de secuencias ordenadas por subsequence, y el conjunto de cuerdas ordenadas por subestring.
- El conjunto de números naturales equipados con la relación de la divisibilidad. (véase Fig.3 y Fig.6)
- El vértice conjunto de un gráfico acíclico dirigido ordenado por la posibilidad de alcanzar.
- El conjunto de subespacios de un espacio vectorial ordenado por la inclusión.
- Para un conjunto parcialmente ordenado P, el espacio de secuencia que contiene todas las secuencias de elementos de P, donde secuencia a precede a la secuencia b si cada artículo en a precede el elemento correspondiente en b. Formalmente, ()an)n▪ ▪ N≤ ≤ ()bn)n▪ ▪ N{displaystyle left(a_{n}right)_{nin mathbb {N}leq left(b_{n}right)_{nin mathbb {N} si an≤ ≤ bn{displaystyle a_{n}leq B_{n} para todos n▪ ▪ N{displaystyle nin mathbb {N}; es decir, una orden de componente.
- Para un set X y un conjunto parcialmente ordenado P, el espacio de función que contiene todas las funciones desde X a P, donde f ≤ g si f()x≤ g()x) para todos x▪ ▪ X.{displaystyle xin X.}
- Una valla, un conjunto parcialmente ordenado definido por una secuencia alternada de relaciones de orden a. b ■ c. d...
- El conjunto de eventos en relatividad especial y, en la mayoría de los casos, relatividad general, donde para dos eventos X y Y, X ≤ Y si Y está en el futuro cono de luz X. Un evento Y sólo puede ser afectada causalmente X si X ≤ Y.
Un ejemplo familiar de un conjunto parcialmente ordenado es una colección de personas ordenadas por descendencia genealógica. Algunas parejas de personas tienen la relación descendiente-ancestro, pero otras parejas de personas son incomparables, sin que ninguna sea descendiente de la otra.
Órdenes sobre el producto cartesiano de conjuntos parcialmente ordenados
En orden de fuerza creciente, es decir, conjuntos de pares decrecientes, tres de los posibles órdenes parciales en el producto cartesiano de dos conjuntos parcialmente ordenados son (ver Fig.4):
- el orden lexicográfico:a, b≤c, dSi a. c oa = c y b ≤ d);
- el pedido del producto: (a, b≤c, dSi a ≤ c y b ≤ d;
- el cierre reflexivo del producto directo de las órdenes estrictas correspondientes: (a, b≤c, dSia. c y b. d) o (a = c y b = d).
Los tres se pueden definir de manera similar para el producto cartesiano de más de dos conjuntos.
Aplicado a espacios vectoriales ordenados sobre el mismo campo, el resultado es en cada caso también un espacio vectorial ordenado.
Ver también órdenes sobre el producto cartesiano de conjuntos totalmente ordenados.
Sumas de conjuntos parcialmente ordenados
Otra forma de combinar dos posets (disjuntos) es la suma ordinal (o suma lineal), Z = X ⊕ Y, definida sobre la unión de los conjuntos subyacentes X e Y por el orden a ≤ Z b si y solo si:
- a, b ▪ X con a ≤X b, o
- a, b ▪ Y con a ≤Y b, o
- a ▪ X y b ▪ Y.
Si dos posets están bien ordenadas, también lo está su suma ordinal.
Los órdenes parciales serie-paralelo se forman a partir de la operación de suma ordinal (en este contexto llamada composición en serie) y otra operación llamada composición en paralelo. La composición paralela es la unión disjunta de dos conjuntos parcialmente ordenados, sin relación de orden entre los elementos de un conjunto y los elementos del otro conjunto.
Nociones derivadas
Los ejemplos usan la pose ()P(){}x,Sí.,z}),⊆ ⊆ ){fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} consistente en el conjunto de todos los subconjuntos de un conjunto de tres elementos {}x,Sí.,z},{displaystyle {x,y,z},} ordenado por inclusión establecida (véase Fig.1).
- a es relacionados con b cuando a ≤ b. Esto no implica que b también está relacionado con a, porque la relación no necesita ser simétrica. Por ejemplo, {}x}{displaystyle {x}} está relacionado con {}x,Sí.},{displaystyle {x,y},} pero no el revés.
- a y b son comparable si a ≤ b o b ≤ a. De lo contrario son incomparable. Por ejemplo, {}x}{displaystyle {x}} y {}x,Sí.,z}{displaystyle {x,y,z} son comparables, mientras que {}x}{displaystyle {x}} y {}Sí.}{displaystyle {y}} no lo son.
- A total o orden lineal es un orden parcial bajo el cual cada par de elementos es comparable, es decir, tricotomía sostiene. Por ejemplo, los números naturales con su orden estándar.
- A cadena es un subconjunto de una pose que es un conjunto totalmente ordenado. Por ejemplo, {}{}},{}x},{}x,Sí.,z}}{displaystyle {fnMicrosoft Sans Serif} es una cadena.
- An Antichain es un subconjunto de una posición en la que no hay dos elementos distintos comparables. Por ejemplo, el conjunto de singletons {}{}x},{}Sí.},{}z}}.{displaystyle {fnMicrosoft Sans Serif}
- Un elemento a se dice que estrictamente inferior a un elemento b, si a ≤ b y aل ل b.{displaystyle aneq b.} Por ejemplo, {}x}{displaystyle {x}} es estrictamente menos que {}x,Sí.}.{displaystyle {x,y}.}
- Un elemento a se dice que cubierto por otro elemento b, escrito a ⋖ b (o a. b), si a es estrictamente menos que b y ningún tercer elemento c encaja entre ellos; formalmente: si ambos a ≤ b y aل ل b{displaystyle aneq b} son verdaderos, y a ≤ c ≤ b es falso para cada uno c con aل ل cل ل b.{displaystyle aneq cneq b.} Usando el orden estricto, la relación a ⋖ b puede ser equivalentemente reformulado como "a. b pero no a. c. b para cualquier c". Por ejemplo, {}x}{displaystyle {x}} está cubierto por{}x,z},{displaystyle {x,z},} pero no está cubierto por {}x,Sí.,z}.{displaystyle {x,y,z}
Extrema
Hay varias nociones de elemento "más grande" y "menos" en una pose P,{displaystyle P,} notablemente:
- El elemento más grande y menos elemento: Un elemento g▪ ▪ P{displaystyle gin P} es un mayor elemento si por cada elemento a▪ ▪ P,a≤ ≤ g.{displaystyle ain P,aleq g.} Un elemento m▪ ▪ P{displaystyle min P} es un elemento mínimo si por cada elemento a▪ ▪ P,m≤ ≤ a.{displaystyle ain P,mleq a.} Un poset sólo puede tener un elemento más grande o menos. En nuestro ejemplo de funcionamiento, el conjunto {}x,Sí.,z}{displaystyle {x,y,z} es el elemento más grande, y {}}{displaystyle {,}} es lo menos.
- Elementos máximos y elementos mínimos: Un elemento g▪ ▪ P{displaystyle gin P} es un elemento maximal si no hay elemento a▪ ▪ P{displaystyle ain P} tales que g.}" xmlns="http://www.w3.org/1998/Math/MathML">a■g.{displaystyle a prendag.}
g.}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/b8cc3a31a30168a980d16dd932e4c4adcdbee6db" style="vertical-align: -0.671ex; width:6.091ex; height:2.176ex;"/> Análogamente, un elemento m▪ ▪ P{displaystyle min P} es un elemento mínimo si no hay elemento a▪ ▪ P{displaystyle ain P} tales que <math alttext="{displaystyle aa.m.{displaystyle aludem.}<img alt="{displaystyle a Si un poset tiene un elemento más grande, debe ser el elemento maximal único, pero de lo contrario puede haber más de un elemento maximal, y de forma similar para elementos menos y elementos mínimos. En nuestro ejemplo, {}x,Sí.,z}{displaystyle {x,y,z} y {}}{displaystyle {,}} son los elementos máximos y mínimos. La eliminación de estos, hay 3 elementos máximos y 3 elementos mínimos (véase Fig.5).
- Límites superiores e inferiores: Para un subconjunto A de P, un elemento x dentro P es un límite superior de A si a≤x, para cada elemento a dentro A. En particular, x necesita no estar A ser un límite superior A. Análogamente, un elemento x dentro P es un límite inferior A si a≥x, para cada elemento a dentro A. Un elemento más grande P es un límite superior de P en sí mismo, y un elemento menos es un límite inferior P. En nuestro ejemplo, el conjunto {}x,Sí.}{displaystyle {x,y}} es un superior para la recogida de elementos {}{}x},{}Sí.}}.{displaystyle {fnMicrosoft Sans Serif}
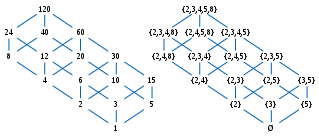
Como otro ejemplo, considere los enteros positivos, ordenados por divisibilidad: 1 es un elemento menos, ya que divide todos los demás elementos; por otro lado, esta pose no tiene un elemento más grande (aunque si uno incluye 0 en la pose, que es un múltiplo de cualquier entero, que sería un elemento más grande; véase Fig.6). Este conjunto parcialmente ordenado ni siquiera tiene elementos maximales, ya que cualquier g divideciones por ejemplo 2g, que es distinto de él, así g no es maximal. Si el número 1 está excluido, manteniendo la divisibilidad como orden en los elementos mayores de 1, entonces la pose resultante no tiene un elemento mínimo, pero cualquier número primo es un elemento mínimo para él. En esta pose, 60 es un límite superior (aunque no un límite inferior) del subconjunto {}2,3,5,10},{displaystyle {2,3,5,10},} que no tiene ningún límite inferior (ya que 1 no está en la pose); por otro lado 2 es un límite inferior del subconjunto de poderes de 2, que no tiene ningún límite superior.
Asignaciones entre conjuntos parcialmente ordenados
Dados dos conjuntos parcialmente ordenados (S, ≤) y (T, ≼), una función f:S→ → T{displaystyle f:Sto T} se llama Orden-preservación, o monotone, o isotone, si para todos x,Sí.▪ ▪ S,{displaystyle x,yin S,} x≤ ≤ Sí.{displaystyle xleq y} implicación f()x≼ f()Sí.). SiU, ≲) es también un conjunto parcialmente ordenado, y ambos f:S→ → T{displaystyle f:Sto T} y g:T→ → U{displaystyle g:Tto U} son pedidos, su composición g∘ ∘ f:S→ → U{displaystyle gcirc f:Sto U} También es el pedido. Una función f:S→ → T{displaystyle f:Sto T} se llama orden-reflexión si para todos x,Sí.▪ ▪ S,{displaystyle x,yin S,} f()x≼ f()Sí.) implica x≤ ≤ Sí..{displaystyle xleq y.}Si f{displaystyle f} es tanto la orden-preservación y el orden-reflexión, entonces se llama un Orden-embedding of (S, ≤) en (T, ≼). En este último caso, f{displaystyle f} es necesariamente inyectable, ya que f()x)=f()Sí.){displaystyle f(x)=f(y)} implicación x≤ ≤ Sí.ySí.≤ ≤ x{displaystyle xleq y{y}yleq x} y a su vez x=Sí.{displaystyle x=y} según la antisimetría ≤ ≤ .{displaystyle leq.} Si un pedido entre dos poses S y T existe, uno dice que S puede ser embebido en T. Si un pedido f:S→ → T{displaystyle f:Sto T} es bijetivo, se llama un orden isomorfismo, y las órdenes parciales (S, ≤) y (T, ≼) se dice que isomorfo. Los pedidos Isomorficos tienen diagramas de Hasse estructuralmente similares (véase Fig.7a). Se puede demostrar que si se conservan mapas f:S→ → T{displaystyle f:Sto T} y g:T→ → U{displaystyle g:Tto U} existen tales g∘ ∘ f{displaystyle gcirc f} y f∘ ∘ g{displaystyle fcirc g} cede la función de identidad en S y T, respectivamente, entonces S y T son orden-isomorfos.
Por ejemplo, un mapeo f:N→ → P()N){displaystyle f:mathbb {N} to mathbb {P} (mathbb {N})} desde el conjunto de números naturales (ordenados por la divisibilidad) al conjunto de potencia de números naturales (ordenados por la inclusión establecida) se puede definir tomando cada número al conjunto de sus primeros divisores. Es la orden-preservación: si x{displaystyle x} divideciones Sí.,{displaystyle y,} entonces cada divisor principal x{displaystyle x} es también un divisor primario de Sí..{displaystyle y.} Sin embargo, no es inyectable (ya que mapea tanto 12 como 6 a {}2,3}{displaystyle {2,3}}) ni reflexión del orden (ya que 12 no divide 6). Tomando en su lugar cada número al conjunto de sus primeros divisores de potencia define un mapa g:N→ → P()N){displaystyle g:mathbb {N} to mathbb {P} (mathbb {N})} que es el orden-preservar, el orden-reflexión, y por lo tanto un orden-embedding. No es un orden-isomorfismo (ya que, por ejemplo, no mapea ningún número al conjunto {}4}{displaystyle {4}}), pero se puede hacer uno restringiendo su codomain to g()N).{displaystyle g(mathbb {N})} Fig.7b muestra un subconjunto de N{displaystyle mathbb {N} y su imagen isomorfa bajo g.{displaystyle g.} La construcción de tal orden-isomorfismo en un conjunto de poder se puede generalizar a una amplia clase de órdenes parciales, llamadas celos distributivos, ver "Teorema de representación de Birkhoff".
Número de pedidos parciales
La secuencia A001035 en OEIS da el número de órdenes parciales en un conjunto de n elementos etiquetados:
| Miembros | Cualquier | Transitive | Reflexivo | Simétrico | Preorden | Orden parcial | Total preordenado | Orden total | Equivalencia relación |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 2 | 2 | 1 | 2 | 1 | 1 | 1 | 1 | 1 |
| 2 | 16 | 13 | 4 | 8 | 4 | 3 | 3 | 2 | 2 |
| 3 | 512 | 171 | 64 | 64 | 29 | 19 | 13 | 6 | 5 |
| 4 | 65.536 | 3.994 | 4.096 | 1.024 | 355 | 219 | 75 | 24 | 15 |
| n | 2n2 | 2n2−n | 2n()n+1)/2 | .. k=0nk!S()n,k){textstyle sum ¡No! | n! | .. k=0nS()n,k){textstyle sum _{k=0} {n} S(n,k)} | |||
| OEIS | A002416 | A006905 | A053763 | A006125 | A000798 | A001035 | A000670 | A000142 | A000110 |
Tenga en cuenta que S(n, k) se refiere a los números de Stirling del segundo tipo
El número de órdenes parciales estrictas es el mismo que el de órdenes parciales.
Si el conteo se hace solo hasta el isomorfismo, la secuencia 1, 1, 2, 5, 16, 63, 318,... (secuencia A000112 en el OEIS) se obtiene.
Extensión lineal
Una orden parcial ≤ ≤ Alternativa Alternativa {displaystyle leq ^{*} en un set X{displaystyle X} es un extensión de otro orden parcial ≤ ≤ {displaystyle leq } on X{displaystyle X} en todos los elementos x,Sí.▪ ▪ X,{displaystyle x,yin X,} siempre x≤ ≤ Sí.,{displaystyle xleq y,} es también el caso de que x≤ ≤ Alternativa Alternativa Sí..{displaystyle xleq ^{*}y.} Una extensión lineal es una extensión que también es un orden lineal (es decir, total). Como ejemplo clásico, el orden léxicográfico de conjuntos totalmente ordenados es una extensión lineal de su pedido de productos. Cada orden parcial puede extenderse a un orden total (principio de extensión ordenada).
En informática, los algoritmos para encontrar extensiones lineales de órdenes parciales (representadas como las órdenes de accesibilidad de gráficos acíclicos dirigidos) se denominan clasificación topológica.
Gráficos acíclicos dirigidos
Las órdenes parciales estrictas corresponden directamente a gráficos acíclicos dirigidos (DAGs). Si se construye un gráfico tomando cada elemento P{displaystyle P} ser un nodo y cada elemento ≤ ≤ {displaystyle leq } para ser un borde, entonces cada orden parcial estricto es un DAG, y el cierre transitivo de un DAG es un orden parcial estricto y también un DAG mismo. En contraste, un orden parcial no restringido tendría bucles propios en cada nodo y por lo tanto no sería un DAG.
En teoría de categorías
Cada pose (y cada conjunto preordenado) puede ser considerado como una categoría donde, para objetos x{displaystyle x} y Sí.,{displaystyle y,} hay en la mayoría un morfismo de x{displaystyle x} a Sí..{displaystyle y.} Más explícitamente, dejar hom(x, Sí.*x, Sí.Si x ≤ Sí. (y de otro modo el set vacío) y ()Sí.,z)∘ ∘ ()x,Sí.)=()x,z).{displaystyle (y,z)circ (x,y)=(x,z). } Tales categorías se denominan a veces posetal.
Los posets son equivalentes entre sí si y solo si son isomorfos. En un poset, el elemento más pequeño, si existe, es un objeto inicial, y el elemento más grande, si existe, es un objeto terminal. Además, cada conjunto pedido por adelantado es equivalente a un poset. Finalmente, cada subcategoría de un poset es isomorfismo cerrado.
Órdenes parciales en espacios topológicos
Si P{displaystyle P} es un conjunto parcialmente ordenado que también se ha dado la estructura de un espacio topológico, entonces es costumbre asumir que {}()a,b):a≤ ≤ b}{displaystyle {(a,b):aleq B} es un subconjunto cerrado del espacio de productos topológicos P× × P.{displaystyle Ptimes P.} Bajo esta suposición las relaciones de orden parcial se comportan bien en los límites en el sentido de que si limi→ → JUEGO JUEGO ai=a,{displaystyle lim _{ito infty }a_{i}=a,} y limi→ → JUEGO JUEGO bi=b,{displaystyle lim _{ito infty }b_{i}=b,} y para todos i,{displaystyle i,} ai≤ ≤ bi,{displaystyle a_{i}leq B_{i},} entonces a≤ ≤ b.{displaystyle aleq b.}
Intervalos
Un intervalo en un poset P es un subconjunto I de P con la propiedad de que, para cualquier x e y en I y cualquier z en P, si x ≤ z ≤ y, entonces z también está en I. (Esta definición generaliza la definición de intervalo para números reales).
Para a ≤ b, el intervalo cerrado [a, b] es el conjunto de elementos x que satisfacen a ≤ x ≤ b (es decir, a ≤ x y x ≤ b). Contiene al menos los elementos a y b.
Usando la relación estricta correspondiente "<", el intervalo abierto (a, b) es el conjunto de elementos x que satisfacen a < x < b (es decir, a < x y x < b). Un intervalo abierto puede estar vacío incluso si a < b. Por ejemplo, el intervalo abierto (0, 1) en los enteros está vacío ya que no hay enteros I tal que 0 < I < 1.
Los intervalos semiabiertos [a, b) y (a, b] se definen de manera similar.
A veces, las definiciones se amplían para permitir a > b, en cuyo caso el intervalo está vacío.
Un intervalo I está atado si existen elementos a,b▪ ▪ P{displaystyle a,bin P} tales que I ⊆ [a, b]. Cada intervalo que puede ser representado en notación de intervalos está obviamente ligado, pero el converso no es cierto. Por ejemplo, vamos P = (0, 1) ∪ (1, 2) ∪ (2, 3) como un subposito de los números reales. El subconjunto (1, 2) es un intervalo atado, pero no tiene infimum o supremum en P, por lo que no puede ser escrito en notación de intervalos utilizando elementos de P.
Una pose se llama localmente finita si cada intervalo ligado es finito. Por ejemplo, los enteros son localmente finitos bajo su orden natural. El orden lexicográfico sobre el producto cartesiano N× × N{displaystyle mathbb {N} times mathbb {N} no es localmente finito, ya (1, 2) ≤ (1, 3) ≤ (1, 4) ≤ (1, 5) ≤ (2, 1). Usando la notación de intervalos, la propiedad "a está cubierto por b"se puede reformular equivalentemente [a,b]={}a,b}.{displaystyle [a,b]={a,b}
Este concepto de intervalo en una orden parcial no debe confundirse con la clase particular de órdenes parciales conocidas como órdenes de intervalo.
Contenido relacionado
Atlas (topología)
Tomaž Pisanski
Día Pi


















































































































![{displaystyle [a,b]={a,b}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c22504982538e7e532e76ad1ebfafd8abd6bb8f2)