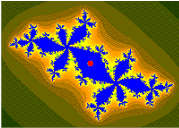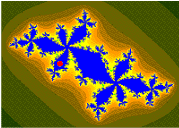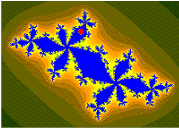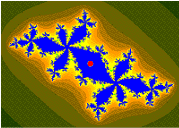
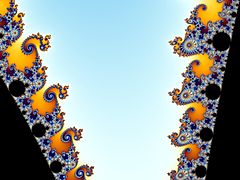
Conjunto de Mandelbrot

El conjunto Mandelbrot (negro) dentro de un entorno de colores continuos

Mandelbrot animación basado en un número estático de iteraciones por pixel

Mandelbrot set detail

El Mandelbrot set () is the set of complex numbers c{displaystyle c} para la cual la función fc()z)=z2+c{displaystyle f_{c}(z)=z^{2}+c} no se sumerge al infinito cuando se z=0{displaystyle z=0}, es decir, para la cual la secuencia fc()0){displaystyle f_{c}(0)}, fc()fc()0)){displaystyle f_{c}(f_{c}(0)}, etc., permanece atado en valor absoluto.

Este conjunto fue definido y dibujado por primera vez por Robert W. Brooks y Peter Matelski en 1978, como parte de un estudio de los grupos kleinianos. Posteriormente, en 1980, Benoit Mandelbrot obtuvo visualizaciones de alta calidad del conjunto mientras trabajaba en el Centro de Investigación Thomas J. Watson de IBM en Yorktown Heights, Nueva York.

Zoom en el límite del conjunto Mandelbrot

Imágenes del conjunto Mandelbrot exhiben un límite elaborado e infinitamente complicado que revela progresivamente cada vez más detalles recursivos en aumentos; matemáticamente, uno diría que el límite del conjunto Mandelbrot es un curva fractal. El "estilo" de este detalle recursivo depende de la región del límite establecido siendo examinado. Las imágenes de conjunto de Mandelbrot se pueden crear mostrando los números complejos y las pruebas, para cada punto de muestra c,{displaystyle c,} si la secuencia fc()0),fc()fc()0)),...... {displaystyle f_{c}(0),f_{c}(f_{c}(0)),dotsc va al infinito. Tratando las partes reales e imaginarias de c{displaystyle c} como coordenadas de imagen en el plano complejo, los píxeles pueden entonces ser coloreados según cuán pronto la secuencia Silenciofc()0)Silencio,Silenciofc()fc()0))Silencio,...... {displaystyle Silenciof_{c}(0) cruza un umbral elegido arbitrariamente (el umbral tiene que ser al menos 2, ya que -2 es el número complejo con la mayor magnitud dentro del conjunto, pero de lo contrario el umbral es arbitrario). Si c{displaystyle c} se mantiene constante y el valor inicial z{displaystyle z} es variado en cambio, uno obtiene el correspondiente Julia set para el punto c{displaystyle c}.

El conjunto de Mandelbrot se ha vuelto popular fuera de las matemáticas tanto por su atractivo estético como por ser un ejemplo de una estructura compleja que surge de la aplicación de reglas simples. Es uno de los ejemplos más conocidos de visualización matemática, belleza matemática y motivo.

Historia

La primera imagen publicada del conjunto Mandelbrot, de Robert W. Brooks y Peter Matelski en 1978

El conjunto de Mandelbrot tiene su origen en la dinámica compleja, un campo investigado por primera vez por los matemáticos franceses Pierre Fatou y Gaston Julia a principios del siglo XX. Este fractal fue definido y dibujado por primera vez en 1978 por Robert W. Brooks y Peter Matelski como parte de un estudio de los grupos kleinianos. El 1 de marzo de 1980, en el Centro de Investigación Thomas J. Watson de IBM en Yorktown Heights, Nueva York, Benoit Mandelbrot vio por primera vez una visualización del set.

Mandelbrot estudió el espacio de parámetros de los polinomios cuadráticos en un artículo que apareció en 1980. El estudio matemático del conjunto de Mandelbrot realmente comenzó con el trabajo de los matemáticos Adrien Douady y John H. Hubbard (1985), quienes establecieron muchos de sus principios fundamentales. propiedades y nombró el conjunto en honor a Mandelbrot por su influyente trabajo en geometría fractal.

Los matemáticos Heinz-Otto Peitgen y Peter Richter se hicieron famosos por promocionar el conjunto con fotografías, libros (1986) y una exposición itinerante internacional del Goethe-Institut alemán (1985).

El artículo de portada del Scientific American de agosto de 1985 presentó a una amplia audiencia el algoritmo para calcular el conjunto de Mandelbrot. La portada fue creada por Peitgen, Richter y Saupe en la Universidad de Bremen. El conjunto de Mandelbrot se hizo prominente a mediados de la década de 1980 como una demostración de gráficos por computadora, cuando las computadoras personales se volvieron lo suficientemente potentes como para trazar y mostrar el conjunto en alta resolución.

El trabajo de Douady y Hubbard coincidió con un gran aumento en el interés por la dinámica compleja y las matemáticas abstractas, y el estudio del conjunto de Mandelbrot ha sido una pieza central de este campo desde entonces. Una lista exhaustiva de todos los que han contribuido a la comprensión de este conjunto desde entonces es larga, pero incluiría a Jean-Christophe Yoccoz, Mitsuhiro Shishikura, Curt McMullen, John Milnor y Mikhail Lyubich.

Definición formal

El conjunto Mandelbrot es el conjunto de valores c en el plano complejo para el cual la órbita del punto crítico z=0{textstyle z=0} debajo de la iteración del mapa cuadrático

zn+1=zn2+c{displaystyle z_{n+1}=z_{n}{2}+c}

permanece atado. Así, un número complejo c es miembro del conjunto Mandelbrot si, al comenzar con z0=0{displaystyle z_{0}=0} y la aplicación de la iteración repetidamente, el valor absoluto zn{displaystyle z_{n} permanece obligado a todos 0}" xmlns="http://www.w3.org/1998/Math/MathML">n■0{displaystyle n confiado0}0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/27a6a5d982d54202a14f111cb8a49210501b2c96" style="vertical-align: -0.338ex; width:5.656ex; height:2.176ex;"/>.

Por ejemplo, c = 1, la secuencia es 0, 1, 2, 5, 26..., que tiende a infinito, así que 1 no es un elemento del conjunto Mandelbrot. Por otro lado, por c=− − 1{displaystyle c=-1}, la secuencia es 0, -1, 0, -1, 0,..., que está ligada, así que -1 pertenece al conjunto.

El conjunto Mandelbrot también se puede definir como el lacus de conexión de la familia de polinomios cuadráticos f()z)=z2+c{displaystyle f(z)=z^{2}+c}, el subconjunto del espacio de parámetros c{displaystyle c} para el cual el conjunto Julia del polinomio correspondiente forma un conjunto conectado. De la misma manera, el límite del conjunto Mandelbrot se puede definir como el locus de bifurcación de esta familia cuadrática, el subconjunto de parámetros cerca de los cuales el comportamiento dinámico del polinomio (cuando se iteró repetidamente) cambia drásticamente.

Propiedades básicas

El conjunto Mandelbrot es un conjunto compacto, ya que está cerrado y contenido en el disco cerrado del radio 2 alrededor del origen. Más específicamente, un punto c{displaystyle c} pertenece al conjunto Mandelbrot si y sólo si SilencioznSilencio≤ ≤ 2{displaystyle TENS_{n} 2} para todos n≥ ≥ 0{displaystyle ngeq 0}. En otras palabras, el valor absoluto zn{displaystyle z_{n} debe permanecer en o debajo de 2 c{displaystyle c} para estar en el conjunto Mandelbrot, M{displaystyle M}, y si ese valor absoluto excede 2, la secuencia escapará al infinito. Desde c=z1{displaystyle c=z_{1}, sigue que SilenciocSilencio≤ ≤ 2{displaystyle Silencioso, estableciendo que c{displaystyle c} siempre estará en el disco cerrado del radio 2 alrededor del origen.

Correspondencia entre el conjunto Mandelbrot y el diagrama de bifurcación del mapa logístico

Con zn{displaystyle z_{n} iterates trazados en el eje vertical, el conjunto Mandelbrot se puede ver para bifurcar donde el conjunto es finito.

La intersección de M{displaystyle M} con el eje real es precisamente el intervalo [− − 2,14]{displaystyle [-2,{frac {1}{4}}}. Los parámetros a lo largo de este intervalo se pueden poner en una correspondencia única con los de la familia logística real,

xn+1=rxn()1− − xn),r▪ ▪ [1,4].{displaystyle x_{n+1}=rx_{n}(1-x_{n}),quad rin [1,4].}

La correspondencia está dada por

z=r()12− − x),c=r2()1− − r2).{displaystyle z=rleft({frac {1}{2}-xright),quad c={frac} {r}{2}left(1-{frac {r}right).}

De hecho, esto da una correspondencia entre todo el espacio de parámetros de la familia logística y el del conjunto de Mandelbrot.

Douady y Hubbard han demostrado que el conjunto Mandelbrot está conectado. De hecho, construyeron un isomorfismo conformal explícito entre el complemento del conjunto Mandelbrot y el complemento del disco de unidad cerrada. Mandelbrot había originalmente conjeturado que el conjunto Mandelbrot está desconectado. Esta conjetura se basó en imágenes de ordenador generadas por programas que no pueden detectar los filamentos delgados que conectan diferentes partes de M{displaystyle M}. Tras nuevos experimentos, revisó su conjetura y decidió que M{displaystyle M} Debería estar conectado. También existe una prueba topológica de la conexión que fue descubierta en 2001 por Jeremy Kahn.

Rayos externos de velas cerca del período 1 continente en el conjunto Mandelbrot

La fórmula dinámica para la uniformización del complemento del conjunto Mandelbrot, derivada de la prueba de Douady y Hubbard de la conexión M{displaystyle M}, da lugar a los rayos externos del conjunto Mandelbrot. Estos rayos se pueden utilizar para estudiar el conjunto Mandelbrot en términos combinatorios y formar la columna vertebral del parapuzzle Yoccoz.

Como se mencionó anteriormente en el artículo, el límite del conjunto Mandelbrot es el locus de bifurcación de la familia de polinomios cuadráticos. En otras palabras, el límite del conjunto Mandelbrot es el conjunto de todos los parámetros c{displaystyle c} para el cual la dinámica del mapa cuadrático zn=zn− − 12+c{displaystyle z_{n}=z_{n-1} {2}+c} exhibe una dependencia sensible de c,{displaystyle c,} i.e., changes abruptly under arbitrarily small changes of c.{displaystyle c.} Se puede construir como el conjunto límite de una secuencia de curvas algebraicas plano, el curvas Mandelbrot, del tipo general conocido como lemniscates polinomio. Las curvas Mandelbrot se definen mediante el ajuste p0=z,pn+1=pn2+z{displaystyle p_{0}=z, P_{n+1}=p_{n}{2}+z}, e interpretar el conjunto de puntos Silenciopn()z)Silencio=2{displaystyle Silenciop_{n}(z) en el plano complejo como una curva en el plano cartesiano real 2n+1{displaystyle 2^{n+1}dentro x y Sí.. Cada curva 0}" xmlns="http://www.w3.org/1998/Math/MathML">n■0{displaystyle n confiado0}0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/27a6a5d982d54202a14f111cb8a49210501b2c96" style="vertical-align: -0.338ex; width:5.656ex; height:2.176ex;"/> es el mapeo de un círculo inicial de radio 2 bajo pn{displaystyle P_{n}. Estas curvas algebraicas aparecen en imágenes del conjunto Mandelbrot computed utilizando el " algoritmo de tiempo de escaneo" mencionado a continuación.

Otras propiedades

Bombillas principales cardioides y de época

Períodos de componentes hiperbólicos

Al mirar una imagen del conjunto Mandelbrot, uno nota inmediatamente la gran región cardioide en el centro. Esto cardioide principales la región de parámetros c{displaystyle c} para el cual el mapa

fc()z)=z2+c{displaystyle f_{c}(z)=z^{2}+c}

tiene un punto fijo de atracción. Consta de todos los parámetros de la forma

c()μ μ ):=μ μ 2()1− − μ μ 2){displaystyle c(mu):={frac {mu}{2}left(1-{frac {mu}{2}}right)}

para algunos μ μ {displaystyle mu } en el disco de unidad abierta.

A la izquierda del cardioide principal, unido a él en el punto c=− − 3/4{displaystyle c=-3/4}, una circular bulbo llamado período-2 es visible. La razón del nombre es que la bombilla consiste precisamente en esos parámetros c{displaystyle c} para la cual fc{displaystyle f_{c} tiene un ciclo de atracción del período 2. Es de hecho el círculo lleno de radio 1/4 centrado alrededor −1.

Más generalmente, por cada entero positivo 2}" xmlns="http://www.w3.org/1998/Math/MathML">q■2{displaystyle q confía2}2}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/a51ff72f66c28051a819a034dea86997914ab599" style="vertical-align: -0.671ex; width:5.33ex; height:2.509ex;"/>, hay φ φ ()q){displaystyle phi (q)} bulbos circulares tangente al cardioide principal llamado bombillas de período-q (donde) φ φ {displaystyle phi } denota la función Euler phi), que consiste en parámetros c{displaystyle c} para la cual fc{displaystyle f_{c} tiene un ciclo de atracción del período q{displaystyle q}. Más específicamente, para cada primitivo q{displaystyle q}raíz de la unidad r=e2π π ipq{displaystyle r=e^{2pi I{frac {}}} (donde) <math alttext="{displaystyle 0<{frac {p}{q}}0.pq.1{displaystyle 0 realizadas{frac {} {} {c}Se hizo 1}<img alt="{displaystyle 0<{frac {p}{q}}), hay una bombilla de punto llamado el pq{fnMicroc} {} {}}} bulbo, que es tangente a la cardioide principal en el parámetro

cpq:=c()r)=r2()1− − r2),{displaystyle c_{frac {p}{q}:=c(r)={frac {r}{2}left(1-{frac {r}right)}

Ciclo de atracción en 2/5-bulbos trazado sobre Julia set (animación)

y que contiene parámetros q{displaystyle q}- ciclos con número de rotación combinatoria pq{fnMicroc} {} {}}}. Más precisamente, el q{displaystyle q} periódicos Componentes Fatou que contienen el ciclo de atracción todo toque en un punto común (comúnmente llamado el α α {displaystyle alpha }- Punto fijo). Si etiquetamos estos componentes U0,...... ,Uq− − 1{displaystyle U_{0},dotsU_{q-1} en orientación en sentido contrario, entonces fc{displaystyle f_{c} mapea el componente Uj{displaystyle U_{j} al componente Uj+p()mod⁡ ⁡ q){displaystyle U_{j+p,(operatorname {mod} q)}.

Ciclos de atracción y Julia fija para parámetros en las bombillas 1/2, 3/7, 2/5, 1/3, 1/4 y 1/5

El cambio de comportamiento que ocurre en cpq{displaystyle c_{frac {} {}}} se conoce como una bifurcación: la atracción de puntos fijos "colidos" con un período de repele-q ciclo. Mientras pasamos por el parámetro de bifurcación en el pq{fnMicroc} {} {}}}-bulbo, el punto fijo atractivo se convierte en un punto fijo repelente (el α α {displaystyle alpha }-Punto fijo), y el período-q el ciclo se vuelve atractivo.

Componentes hiperbólicos

Todas las bombillas que encontramos en la sección anterior eran componentes interiores del conjunto Mandelbrot en el que los mapas fc{displaystyle f_{c} tienen un ciclo periódico atractivo. Esos componentes se denominan componentes hiperbólicos.

Se conjetura que estos son los sólo regiones interiores M{displaystyle M}. Este problema, conocido como densidad de hiperbolicidad, puede ser el problema abierto más importante en el campo de la dinámica compleja. Los componentes hipotéticos no hiperbólicos del conjunto Mandelbrot a menudo se denominan componentes "más rápidos" o fantasmas. Para real polinomios cuadráticos, esta pregunta fue contestada positivamente en los años noventa independientemente por Lyubich y por Graczyk y Świątek. (Nota que los componentes hiperbólicos que intersectan el eje real corresponden exactamente a las ventanas periódicas del diagrama Feigenbaum. Así que este resultado indica que tales ventanas existen cerca de cada parámetro en el diagrama.)

No todas las componentes hiperbólicas pueden alcanzarse mediante una secuencia de bifurcaciones directas desde la cardioide principal del conjunto de Mandelbrot. Sin embargo, tal componente puede ser alcanzado por una secuencia de bifurcaciones directas desde el cardioide principal de una pequeña copia de Mandelbrot (ver más abajo).

Cada uno de los componentes hiperbólicos tiene un centro, que es un punto c tal que el dominio Fatou interior para fc()z){displaystyle f_{c}(z)} tiene un ciclo super-atrayendo—es decir, que la atracción es infinita (ver la imagen aquí). Esto significa que el ciclo contiene el punto crítico 0, por lo que 0 se iteró de nuevo a sí mismo después de algunas iteraciones. Por lo tanto, tenemos que fcn()0)=0{displaystyle f_{c}{n}(0)=0} para algunos n. Si llamamos a este polinomio Qn()c){displaystyle Q^{n}(c)} (dejarlo depende de c en lugar de z), tenemos que Qn+1()c)=Qn()c)2+c{displaystyle Q^{n+1}(c)=Q^{n}(c)^{2}+c} y que el grado de Qn()c){displaystyle Q^{n}(c)} es 2n− − 1{displaystyle 2^{n-1}. Por lo tanto, podemos construir los centros de los componentes hiperbólicos resolviendo sucesivamente las ecuaciones Qn()c)=0,n=1,2,3,...{displaystyle Q^{n}(c)=0,n=1,2,3,...}. El número de nuevos centros producidos en cada paso es dado por Sloane OEIS: A000740.

Conectividad local

Se conjetura que el conjunto de Mandelbrot está conectado localmente. Esta famosa conjetura se conoce como MLC (por Mandelbrot conectado localmente). Según el trabajo de Adrien Douady y John H. Hubbard, esta conjetura daría como resultado un simple "disco pellizcado" abstracto; modelo del conjunto de Mandelbrot. En particular, implicaría la importante conjetura de hiperbolicidad mencionada anteriormente.

El trabajo de Jean-Christophe Yoccoz estableció la conectividad local del conjunto Mandelbrot en todos los parámetros finitamente renormalizables; es decir, aproximadamente aquellos que contienen sólo en finitamente muchas copias Mandelbrot pequeñas. Desde entonces, la conectividad local se ha demostrado en muchos otros puntos M{displaystyle M}, pero la conjetura completa sigue abierta.

Autosimilitud

Auto-similaridad en el conjunto Mandelbrot mostrado mediante el zoom en una función redonda mientras que el panning en el negativo-x dirección. El centro de pantallas izquierda de la quinta a la séptima función redonda (-1.4002, 0) a (-1.4011, 0) mientras que la vista aumenta por un factor de 21.78 para aproximar la plaza de la relación Feigenbaum δ δ {displaystyle delta }.

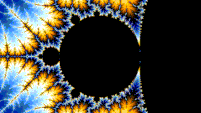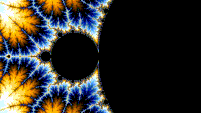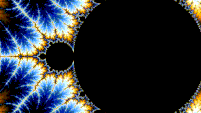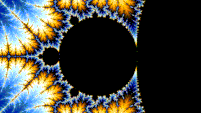
El conjunto de Mandelbrot es autosimilar bajo aumento en las proximidades de los puntos de Misiurewicz. También se conjetura que es autosimilar en torno a los puntos de Feigenbaum generalizados (p. ej., −1,401155 o −0,1528 + 1,0397i), en el sentido de converger en un conjunto límite. El conjunto de Mandelbrot en general no es estrictamente autosimilar, pero es casi autosimilar, ya que se pueden encontrar pequeñas versiones ligeramente diferentes de sí mismo en escalas arbitrariamente pequeñas. Estas pequeñas copias del conjunto de Mandelbrot son ligeramente diferentes, principalmente debido a los hilos delgados que las conectan con el cuerpo principal del conjunto.

Más resultados

La dimensión de Hausdorff del límite del conjunto de Mandelbrot es igual a 2 según lo determinado por un resultado de Mitsuhiro Shishikura. El hecho de que sea mayor (en un número entero) que su dimensión topológica (que es 1) refleja la naturaleza fractal del límite del conjunto de Mandelbrot. De hecho, el resultado de Shishikura establece intuitivamente que el límite establecido de Mandelbrot es tan 'ondulante' que se las arregla para llenar localmente el espacio tan eficientemente como una región plana bidimensional. Esto abre la posibilidad potencial de que el límite del conjunto de Mandelbrot, a pesar de ser una curva, tenga un área diferente de cero (o, más formalmente, tenga una medida de Lebesgue planar positiva). Si este es realmente el caso o no, sigue siendo un problema abierto en la actualidad.

Se ha demostrado que el Mandelbrot generalizado establecido en espacios de número hipercomplex de alta dimensión (es decir, cuando el poder α α {displaystyle alpha } de la variable iterada z{displaystyle z} tiende a la infinidad) es convergente a la unidad (α α {displaystyle alpha }-1)-sfera.

En el modelo de computación real de Blum-Shub-Smale, el conjunto de Mandelbrot no es computable, pero su complemento es computable enumerable. Sin embargo, muchos objetos simples (por ejemplo,, el gráfico de exponenciación) tampoco son computables en el modelo BSS. En la actualidad, se desconoce si el conjunto de Mandelbrot es computable en modelos de computación real basados en análisis computable, que se corresponden más con la noción intuitiva de "trazar el conjunto por computadora". Hertling ha demostrado que el conjunto de Mandelbrot es computable en este modelo si la conjetura de hiperbolicidad es cierta.

Relación con los conjuntos de Julia

Un mosaico hecho al igualar Julia pone a sus valores de c en el plano complejo. Usando esto, se puede ver que la forma del conjunto Mandelbrot se forma. Esto es porque el conjunto Mandelbrot es en sí mismo un mapa de los conjuntos de Julia conectados.

Como consecuencia de la definición del conjunto de Mandelbrot, existe una estrecha correspondencia entre la geometría del conjunto de Mandelbrot en un punto dado y la estructura del conjunto de Julia correspondiente. Por ejemplo, un valor de c pertenece al conjunto de Mandelbrot si el conjunto de Julia correspondiente es conexo. Por lo tanto, el conjunto de Mandelbrot puede verse como un mapa de los conjuntos de Julia conectados.

Este principio se explota en prácticamente todos los resultados profundos en el set de Mandelbrot. Por ejemplo, Shishikura demostró que, para un conjunto denso de parámetros en el límite del conjunto de Mandelbrot, el conjunto de Julia tiene una dimensión de Hausdorff dos y luego transfiere esta información al plano de parámetros. De manera similar, Yoccoz primero probó la conectividad local de los conjuntos de Julia, antes de establecerla para el conjunto de Mandelbrot en los parámetros correspondientes. Adrien Douady resume elocuentemente este principio como:

Plough en el plano dinámico, y cosecha en el espacio del parámetro.

Geometría

Por cada número racional pq{fnMicroc} {} {}}}, donde p y q son relativamente primos, un componente hiperbólico del período q bifurca desde el cardioide principal en un punto en el borde del cardioide correspondiente a un ángulo interno 2π π pq{displaystyle {tfrac {2ccccccccc\cc\cc\cc\\ccc\c\\c\\\\\\c\\\\\\\c\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ {}}}. La parte del conjunto Mandelbrot conectado al cardioide principal en este punto de bifurcación se llama el p/q- Sube.. Los experimentos informáticos sugieren que el diámetro de la extremidad tiende a cero como 1q2{displaystyle {tfrac {}{q^{2}}} {f}}} {f}}} {f}}}} {f}}}}} {f}}}}}}} {f}}}}}. La mejor estimación actual conocida es la Calidad de Yoccoz, que indica que el tamaño tiende a cero como 1q{fnMicroc} {1}{q}}.

Un período...q miembro tendrá q− − 1{displaystyle q-1} "antena" en la parte superior de su extremidad. Así podemos determinar el período de una bombilla dada contando estas antenas. También podemos encontrar el numerador del número de rotación, p, numerando cada antena en sentido contrario de la extremidad de 1 a q− − 1{displaystyle q-1} y encontrar qué antena es la más corta.

Pi en el conjunto de Mandelbrot

En un intento de demostrar que el espesor del p/q- La tumba es cero, David Boll llevó a cabo un experimento informático en 1991, donde computó el número de iteraciones requeridas para la serie para divergencia z=− − 34+iε ε {displaystyle z=-{tfrac {3}{4}+ivarepsilon } ()− − 34{displaystyle -{tfrac {3}{4}} siendo su ubicación). Como la serie no se sumerge para el valor exacto z=− − 34{displaystyle z=-{tfrac {3}{4}}, el número de iteraciones requerido aumentos con un pequeño ε ε {displaystyle varepsilon }. Resulta que multiplicar el valor ε ε {displaystyle varepsilon } con el número de iteraciones requeridas produce una aproximación π π {displaystyle pi} que se hace mejor para más pequeño ε ε {displaystyle varepsilon }. Por ejemplo, ε ε {displaystyle varepsilon } = 0.0000001 el número de iteraciones es 31415928 y el producto es 3.1415928. En 2001, Aaron Klebanoff demostró el descubrimiento de Boll.

Secuencia de Fibonacci en el conjunto de Mandelbrot

Se puede demostrar que la secuencia de Fibonacci se encuentra dentro del conjunto Mandelbrot y que existe una relación entre el cardioide principal y el Diagrama Farey. Al mapear el cardioide principal a un disco, se puede notar que la cantidad de antenas que se extiende desde el siguiente componente hiperbólico más grande, y que se encuentra entre los dos componentes previamente seleccionados, sigue el traje con la secuencia de Fibonacci. La cantidad de antenae también se correlaciona con el Diagrama Farey y el denominador suma dentro de los valores fraccionales correspondientes, de los cuales se relacionan con la distancia alrededor del disco. Ambas partes de estos valores fraccionados pueden resumirse juntos después de 13{fnMicroc} {1}{3}} para producir la ubicación del siguiente componente Hyperbolic dentro de la secuencia. Así, la secuencia Fibonacci de 1, 2, 3, 5, 8, 13, y 21 se puede encontrar dentro del conjunto Mandelbrot.

Galería de imágenes de una secuencia de zoom

El límite del conjunto de Mandelbrot muestra detalles más complejos cuanto más de cerca se mira o se amplía la imagen, lo que generalmente se denomina "acercamiento". El siguiente ejemplo de una secuencia de imágenes que se acerca a un valor c seleccionado da una impresión de la infinita riqueza de diferentes estructuras geométricas presentes en el límite del conjunto de Mandelbrot y explica algunas de sus reglas típicas.

La ampliación de la última imagen en relación con la primera es de aproximadamente 10¹⁰ a 1. En relación con un monitor de computadora común, representa una sección de un conjunto de Mandelbrot con un diámetro de 4 millones de kilómetros.. Su borde muestra un número astronómico de diferentes estructuras fractales.

• 

  Empieza. Mandelbrot con un entorno de colores continuos.

• 

  Gap entre la "cabeza" y el "cuerpo", también llamado "el valle del mar"

• 

  Doble-spirales a la izquierda, "seahorses" a la derecha

• 

  "Seahorse" al revés

El "cuerpo" del caballito de mar está compuesto por 25 "radios" compuesto por dos grupos de 12 "radios" cada uno y uno "habló" conectando al cardioide principal. Estos dos grupos pueden ser atribuidos por algún tipo de metamorfosis a los dos "dedos" de la "mano superior" del conjunto de Mandelbrot; por lo tanto, el número de "radios" aumenta de un "caballito de mar" al siguiente por 2; el "centro" es un llamado punto de Misiurewicz. Entre la "parte superior del cuerpo" y la "cola" se puede reconocer una pequeña copia distorsionada del conjunto de Mandelbrot llamado satélite.

• 

  El punto final central de la "puerta de caballo" es también un punto Misiurewicz.

• 

  Parte de la cola – sólo hay un camino que consiste en las estructuras delgadas que conducen a través de toda la cola. Este camino de zigzag pasa por los "hubs" de los grandes objetos con 25 "hablas" en la frontera interior y exterior del "tallo"; por lo tanto el conjunto Mandelbrot es un conjunto simplemente conectado, lo que significa que no hay islas y no hay caminos de bucle alrededor de un agujero.

• 

  Satélite. Las dos colas de caballo son el comienzo de una serie de coronas concéntricas con el satélite en el centro.

• 

  Cada una de estas coronas consiste en "puertas cortas" similares; su número aumenta con poderes de 2, un fenómeno típico en el medio ambiente de los satélites. El camino único hacia el centro espiral pasa el satélite desde la ranura del cardioide hasta la parte superior de la "antena" en la "cabeza".

• 

  "Antenna" del satélite. Pueden reconocerse varios satélites de segunda orden.

• 

  El " valle del mar" del satélite. Todas las estructuras desde el inicio del zoom reaparecen.

• 

  Doble-spirales y "seahorses" – a diferencia de la segunda imagen desde el principio, tienen apendices que consisten en estructuras como "puertas de separación"; esto demuestra el vínculo típico de n + 1 estructuras diferentes en el ambiente de satélites del orden n, aquí para el caso más simple n = 1.

• 

  Doble-spirales con satélites de segundo orden – analógicamente a los "seahorses", los doble-spirales pueden ser interpretados como una metamorfosis de la "antena".

• 

  En la parte exterior de los apéndices, las islas de las estructuras pueden ser reconocidas; tienen una forma como Julia establece J_c; el mayor de ellos se puede encontrar en el centro del "doble-hook" en el lado derecho.

• 

  Parte del "doble-hook"

• 

  Islas

• 

  Detalle de una isla

• 

  Detalle de la espiral. Abra esta ubicación en un visor interactivo.

Las islas en el tercer paso al final parecen consistir de infinitamente muchas partes como conjuntos Cantor, como es en realidad el caso del conjunto correspondiente de Julia Jc{displaystyle J_{c}. Sin embargo, están conectados por pequeñas estructuras, por lo que todo representa un conjunto simplemente conectado. Las pequeñas estructuras se encuentran en un satélite en el centro que es demasiado pequeño para ser reconocido en esta magnificación. El valor de c{displaystyle c} para el correspondiente Jc{displaystyle J_{c} no es el del centro de imagen, pero, en relación con el cuerpo principal del conjunto Mandelbrot, tiene la misma posición que el centro de esta imagen en relación con el satélite mostrado en el sexto paso zoom.

Estructura interior

Si bien el conjunto de Mandelbrot generalmente se representa mostrando el detalle del límite exterior, también se puede revelar la estructura dentro del conjunto delimitado. Por ejemplo, al calcular si un valor de c dado está vinculado o no, mientras permanece vinculado, el valor máximo que alcanza este número se puede comparar con el valor de c en esa ubicación. Si se utiliza el método de la suma de cuadrados, el número calculado sería max:(real^2 + imaginary^2) - c:(real^2 + imaginary^2). La magnitud de este cálculo se puede representar como un valor en un gradiente.

Esto produce resultados como los siguientes, degradados con bordes y contornos definidos a medida que se acercan a los límites. Las animaciones sirven para resaltar los límites del degradado.

• 

  Estructura gradiente animada dentro del conjunto Mandelbrot

• 

  Estructura gradiente animada dentro del conjunto Mandelbrot, detalle

• 

  Rendering of progressive iterations from 285 to approximately 200,000 with corresponding bounded gradients animated

• 

  Thumbnail para gradiente en iteraciones progresivas

Generalizaciones

Animaciones del juego Multibrot para d de 0 a 5 (izquierda) y de 0,05 a 2 (derecha).

Un conjunto 4D Julia puede ser proyectado o transversalizado en 3D, y debido a esto es posible un Mandelbrot 4D.

Conjuntos multibrot

Los conjuntos multibrot son conjuntos acotados que se encuentran en el plano complejo para miembros de la familia de recursiones polinómicas univariadas mónicas generales

z↦ ↦ zd+c.{displaystyle zmapsto z^{d}+c.}

Para un entero d, estos conjuntos son loci de conexión para los conjuntos Julia construidos de la misma fórmula. También se ha estudiado la conexión cúbica completa; aquí se considera la recursión de dos parámetros z↦ ↦ z3+3kz+c{displaystyle zmapsto z^{3}+3kz+c}, cuyos dos puntos críticos son las complejas raíces cuadradas del parámetro k. Un parámetro está en el lacus de conexión cúbica si ambos puntos críticos son estables. Para las familias generales de funciones holomorfas, las frontera del conjunto Mandelbrot generaliza al locus de bifurcación, que es un objeto natural para estudiar incluso cuando el locus de conexión no es útil.

El conjunto Multibrot se obtiene por variar el valor del exponente d. El artículo tiene un vídeo que muestra el desarrollo d = 0 a 7, en qué punto hay 6 es decir. ()d− − 1){displaystyle (d-1)} Lobos alrededor del perímetro. En general, cuando d es un entero positivo, la región central en cada uno de estos conjuntos es siempre un epicicloide de ()d− − 1){displaystyle (d-1)} Cusps. Un desarrollo similar con exponentes integrales negativos resulta en ()1− − d){displaystyle (1-d)} clefts en el interior de un anillo, donde la principal región central del conjunto es una hipocicloide de ()1− − d){displaystyle (1-d)} Cusps.

Dimensiones más altas

No hay una extensión perfecta del Mandelbrot establecido en 3D. Esto se debe a que no hay análogo 3D de los números complejos para que se iteren. Sin embargo, hay una extensión de los números complejos en 4 dimensiones, llamadas las quaternions, que crea una extensión perfecta del conjunto Mandelbrot y la Julia se establece en 4 dimensiones. Estos pueden entonces ser cruzados o proyectados en una estructura 3D. Sin embargo, el conjunto de Mandelbrot de cuaternión (4-dimensional) es simplemente un sólido de revolución del conjunto de Mandelbrot 2-dimensional (en el plano j-k), y por lo tanto es en gran parte ininteresante mirar, ya que no tiene ninguna de las propiedades que se espera de un fractal 4-dimensional. Tomando una sección transversal tridimensional en d=0()q=a+bi+cj+dk){displaystyle d=0 (q=a+bi+cj+dk)} resultados en un sólido de la revolución del Mandelbrot 2-dimensional que se encuentra alrededor del eje real.

Otras asignaciones no analíticas

Imagen del Tricorn / Mandelbar fractal

De particular interés es el fractal tricornio, el locus de conexión de la familia anti-holomórfica

z↦ ↦ z̄ ̄ 2+c.{displaystyle zmapsto {bar}{2}+c.}

El tricornio (también llamado a veces Mandelbar) fue encontrado por Milnor en su estudio de segmentos de parámetros de polinomios cúbicos reales. No está no conectado localmente. Esta propiedad es heredada por el lugar geométrico de conexión de los polinomios cúbicos reales.

Otra generalización no analítica es el fractal Burning Ship, que se obtiene iterando lo siguiente:

z↦ ↦ ()SilencioR R ()z)Silencio+iSilencioI I ()z)Silencio)2+c.{displaystyle zmapsto (resistenciaReleft(zright)

Dibujos por ordenador

Existe una multitud de diversos algoritmos para trazar el conjunto de Mandelbrot a través de un dispositivo informático. Aquí, se demostrará el algoritmo más simple y más utilizado, a saber, el ingenuo "algoritmo de tiempo de escape". En el algoritmo de tiempo de escape, se realiza un cálculo repetitivo para cada punto x, y en el área de trazado y, según el comportamiento de ese cálculo, se elige un color para ese píxel

Las ubicaciones x e y de cada punto se utilizan como valores iniciales en un cálculo repetitivo o iterativo (descrito en detalle a continuación). El resultado de cada iteración se utiliza como valor inicial para la siguiente. Los valores se comprueban durante cada iteración para ver si han alcanzado un "escape" crítico. condición, o "rescate". Si se alcanza esa condición, se detiene el cálculo, se dibuja el píxel y se examina el siguiente punto x, y.

El color de cada punto representa la rapidez con la que los valores alcanzaron el punto de escape. A menudo, el negro se usa para mostrar valores que no logran escapar antes del límite de iteración, y gradualmente se usan colores más brillantes para los puntos que escapan. Esto da una representación visual de cuántos ciclos se requirieron antes de alcanzar la condición de escape.

Para hacer tal imagen, la región del plano complejo que estamos considerando está subdividida en un cierto número de píxeles. Para colorear tal pixel, deja c{displaystyle c} ser el punto medio de ese pixel. Ahora iteramos el punto crítico 0 bajo fc{displaystyle f_{c}, comprobando a cada paso si el punto de órbita tiene un radio superior a 2. Cuando este es el caso, sabemos que c{displaystyle c} no pertenece al conjunto Mandelbrot, y coloreamos nuestro píxel según el número de iteraciones usadas para averiguarlo. De lo contrario, seguimos iterando hasta un número fijo de pasos, después de lo cual decidimos que nuestro parámetro es "probablemente" en el conjunto Mandelbrot, o al menos muy cerca de él, y colorear el píxel negro.

En pseudocódigo, este algoritmo tendría el siguiente aspecto. El algoritmo no usa números complejos y simula manualmente operaciones de números complejos usando dos números reales, para aquellos que no tienen un tipo de datos complejo. El programa puede simplificarse si el lenguaje de programación incluye operaciones de tipos de datos complejos.

para cada uno pixel (Px, Py) en la pantalla dox0:= escalada x coordenadas de pixel (escalada para tumbarse en la escala Mandelbrot X (-2.00, 0.47))
y0:= escalada y coordenadas de píxel (escalada para tumbarse en la escala Mandelbrot Y (-1.12, 1.12))
x:= 0,0
y:= 0.0
iteración:= 0
max_iteration:= 1000
 mientras (x*x + y*y ≤ 2*2 Y iteración - max_iteration) doxtemp:= x*x - y*y + x0
y:= 2*x*y + y0
x:= xtemp
iteración:= iteración + 1

color:= paleta[iteración]
plot(Px, Py, color)

Aquí, relacionando el pseudocódigo a c{displaystyle c}, z{displaystyle z} y fc{displaystyle f_{c}:

• z=x+iSí.{displaystyle z=x+iy}
• z2=x2+i2xSí.− − Sí.2{displaystyle z^{2}=x^{2}+i2xy-y^{2}
• c=x0+iSí.0{displaystyle c=x_{0}+iy_{0}

y así, como se puede ver en el pseudocódigo en el cálculo de x e y:

• x=Re⁡ ⁡ ()z2+c)=x2− − Sí.2+x0{displaystyle x=mathop {Re} (z^{2}+c)=x^{2}-y^{2}+x_{0} y Sí.=Im⁡ ⁡ ()z2+c)=2xSí.+Sí.0.{displaystyle y=mathop {mathrm [Im] } (z^{2}+c)=2xy+y_{0}

Para obtener imágenes coloridas del conjunto, la asignación de un color a cada valor del número de iteraciones ejecutadas se puede realizar mediante una variedad de funciones (lineal, exponencial, etc.).

Referencias en la cultura popular

El conjunto de Mandelbrot se considera el fractal más popular y se ha mencionado varias veces en la cultura popular.

• La canción de Jonathan Coulton "Mandelbrot Set" es un tributo tanto al fractal mismo como al hombre que se llama después, Benoit Mandelbrot.
• El segundo libro del Serie de modos por Piers Anthony, Modo de fractura, describe un mundo que es un modelo 3D perfecto del conjunto.
• La novela Arthur C. Clarke El fantasma de los grandes bancos cuenta con un lago artificial hecho para replicar la forma del conjunto Mandelbrot.
• Benoit Mandelbrot y el conjunto eponímico fueron los temas del Google Doodle el 20 de noviembre de 2020 (el 96 cumpleaños del fallecido Benoit Mandelbrot).
• La banda americana de rock Heart tiene una imagen de un Mandelbrot en la portada de su álbum de 2004, Júpiters Darling.
• La banda británica de metal negro Anaal Nathrakh utiliza una imagen que se parece al conjunto Mandelbrot en su arte de la portada de Eschaton.
• La serie de televisión La Agencia Holística de Detectives de Dirk Gently (2016) destaca el conjunto Mandelbrot en conexión con las visiones del personaje Amanda. En la segunda temporada, su chaqueta tiene una gran imagen del fractal en la parte posterior.
• En el libro 2001 de Ian Stewart Flatterland, hay un personaje llamado el Mandelblot, que ayuda a explicar fractales a los personajes y el lector.