Complejidad ciclomática

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

complejidad ciclomática es una métrica de software que se utiliza para indicar la complejidad de un programa. Es una medida cuantitativa del número de rutas linealmente independientes a través del código fuente de un programa. Fue desarrollado por Thomas J. McCabe, Sr. en 1976.

La complejidad ciclomática se calcula utilizando el gráfico de flujo de control del programa: los nodos del gráfico corresponden a grupos indivisibles de comandos de un programa, y un borde dirigido conecta dos nodos si el segundo comando puede ejecutarse inmediatamente después del primero. dominio. La complejidad ciclomática también se puede aplicar a funciones, módulos, métodos o clases individuales dentro de un programa.

Una estrategia de prueba, llamada prueba de ruta básica por McCabe, quien la propuso por primera vez, es probar cada ruta linealmente independiente a través del programa; en este caso, el número de casos de prueba será igual a la complejidad ciclomática del programa.

Descripción

Definición

La complejidad ciclomática de una sección de código fuente es el número de rutas linealmente independientes dentro de ella; un conjunto de caminos es linealmente dependiente si hay un subconjunto de uno (o más) caminos donde la diferencia simétrica de sus conjuntos de bordes está vacía. Si el código fuente no contuviera declaraciones de flujo de control (condicionales o puntos de decisión), la complejidad sería 1, ya que solo habría una ruta única a través del código. Si el código tuviera una declaración IF de una sola condición, habría dos rutas a través del código: una donde la declaración IF es VERDADERA y otra donde es FALSA, por lo que la complejidad sería 2. Dos IF anidados de una sola condición, o un IF con dos condiciones, produciría una complejidad de 3.

La complejidad ciclomática de un programa estructurado se define con referencia al gráfico de flujo de control del programa, un gráfico dirigido que contiene los bloques básicos del programa, con un borde entre dos bloques básicos si el control puede pasar del primero al el segundo. La complejidad $M$ se define entonces como

{displaystyle M=E-N+2P,}

dónde

$E$ = el número de bordes del gráfico.
$N$ = el número de nodos del gráfico.
$P$ = el número de componentes conectados.

Una formulación alternativa es utilizar un gráfico en el que cada punto de salida esté conectado con el punto de entrada. En este caso, el gráfico está fuertemente conectado; la complejidad ciclomática del programa es igual al número ciclomático de su gráfico (también conocido como primer número de Betti), que se define como

{displaystyle M=E-N+P.}

Esto puede verse como calcular el número de ciclos linealmente independientes que existen en el gráfico: aquellos ciclos que no contienen otros ciclos dentro de sí mismos. Debido a que cada punto de salida regresa al punto de entrada, hay al menos un ciclo de este tipo para cada punto de salida.

Para un solo programa (o subrutina o método), $P$ siempre es igual a 1; una fórmula más simple para una sola subrutina es

{displaystyle M=E-N+2.}

La complejidad ciclomática se puede aplicar a varios programas o subprogramas al mismo tiempo (a todos los métodos de una clase, por ejemplo), y en estos casos $P$ será igual al número de programas en cuestión; cada subprograma aparecerá como un subconjunto desconectado del gráfico.

McCabe demostró que la complejidad ciclomática de un programa estructurado con un solo punto de entrada y un punto de salida es igual al número de puntos de decisión (declaraciones "if" o bucles condicionales) contenidos en ese programa más uno. Esto es cierto sólo para los puntos de decisión contados en las instrucciones más bajas a nivel de máquina. Las decisiones que involucran predicados compuestos como los que se encuentran en lenguajes de alto nivel como IF cond1 AND cond2 THEN... deben contarse en términos de variables de predicado involucradas; en este ejemplo, se deben contar dos puntos de decisión porque a nivel de máquina es equivalente a IF cond1 THEN IF cond2 THEN....

La complejidad ciclomática puede extenderse a un programa con múltiples puntos de salida; en este caso es igual a

{displaystyle pi -s+2,}

{displaystyle pi}

s

Topología algebraica

Un subgrafo par de un grafo (también conocido como subgrafo euleriano) es aquel en el que cada vértice incide con un número par de aristas; tales subgrafos son uniones de ciclos y vértices aislados. Los subgrafos se identificarán con sus conjuntos de aristas, lo que equivale a considerar solo aquellos subgrafos pares que contienen todos los vértices del grafo completo.

El conjunto de todos los subgrafos pares de un gráfico está cerrado bajo diferencia simétrica y, por lo tanto, puede verse como un espacio vectorial sobre GF(2); este espacio vectorial se llama espacio de ciclo del gráfico. El número ciclomático del gráfico se define como la dimensión de este espacio. Dado que GF(2) tiene dos elementos y el espacio del ciclo es necesariamente finito, el número ciclomático también es igual al 2-logaritmo del número de elementos en el espacio del ciclo.

Una base para el espacio del ciclo se construye fácilmente mediante la primera fijación de un bosque azotado del gráfico, y luego considerando los ciclos formados por un borde no en el bosque y el camino en el bosque que conecta los puntos finales de ese borde; estos ciclos forman una base para el espacio del ciclo. El número ciclomático también equivale al número de bordes no en un bosque de azotes maximal de un gráfico. Puesto que el número de bordes en un bosque de azotes maximal de un gráfico es igual al número de vértices menos el número de componentes, la fórmula ${displaystyle E-N+P}$ para el número ciclomático sigue.

La complejidad ciclomática también se puede definir como un número de Betti relativo, el tamaño de un grupo de homología relativo:

{displaystyle M:=b_{1}(G,t):=operatorname {rank} H_{1}(G,t),}

que se lee como "el rango del primer grupo de homología del gráfico G en relación con los nodos terminales|Terminología t". Esta es una forma técnica de decir "el número de caminos linealmente independientes a través del gráfico de flujo desde una entrada hasta una salida", donde:

"independiente lineal" corresponde a la homología; el retroceso no es doble
"patos" corresponde a la primera homología; un camino es un objeto unidimensional
"relativo" significa que el camino debe comenzar y terminar en un punto de entrada (o salida).

Esta complejidad ciclomática se puede calcular. También se puede computar a través del número Betti absoluto identificando los nodos terminales en un componente dado, o los caminos de dibujo que conectan las salidas a la entrada. El nuevo gráfico aumentado ${displaystyle {tilde {}}}$ obtenido

{displaystyle M=b_{1} {G}=fnMicrosoftware {rank} H_{1}({tilde {G}}}

También se puede computar a través de homotopy. Si un gráfico de flujo de control (conectado) se considera un complejo CW unidimensional llamado ${displaystyle X}$ , el grupo fundamental ${displaystyle X}$ será ${displaystyle pi _{1}(X)cong mathbb {Z} ^{*n}$ . El valor de ${displaystyle n+1}$ es la complejidad ciclomática. El grupo fundamental cuenta cuántos bucles hay a través del gráfico hasta la homotopy, alineando como se esperaba.

Interpretación

En su presentación "Métricas de calidad del software para identificar riesgos" Para el Departamento de Seguridad Nacional, Tom McCabe presenta la siguiente categorización de complejidad ciclomática:

1 - 10: Procedimiento simple, poco riesgo
11 - 20: Riesgo más complejo y moderado
21 - 50: Complejo, alto riesgo
■ 50: Código intestable, muy alto riesgo

Aplicaciones

Limitar la complejidad durante el desarrollo

Una de las aplicaciones originales de McCabe era limitar la complejidad de las rutinas durante el desarrollo del programa; Recomendó que los programadores contaran la complejidad de los módulos que están desarrollando y los dividieran en módulos más pequeños siempre que la complejidad ciclomática del módulo excediera 10. Esta práctica fue adoptada por la metodología de pruebas estructuradas del NIST, con una observación que desde McCabe' Según la publicación original, la cifra de 10 había recibido evidencia sustancial que la corrobora, pero que en algunas circunstancias puede ser apropiado relajar la restricción y permitir módulos con una complejidad tan alta como 15. Como la metodología reconocía que había razones ocasionales para ir más allá del límite acordado, formuló su recomendación como "Para cada módulo, limite la complejidad ciclomática a [el límite acordado] o proporcione una explicación por escrito de por qué se excedió el límite".

Medir la "estructuración" de un programa

La sección VI del artículo de McCabe de 1976 se ocupa de determinar cómo se ven los gráficos de flujo de control (CFG) de programas no estructurados en términos de sus subgrafos, que McCabe identifica. (Para obtener detalles sobre esa parte, consulte el teorema del programa estructurado). McCabe concluye esa sección proponiendo una medida numérica de qué tan cerca del ideal de programación estructurada está un programa dado, es decir, su "estructuración" utilizando el neologismo de McCabe. McCabe calificó la medida que ideó para este propósito como de complejidad esencial.

Para calcular esta medida, el CFG original se reduce iterativamente identificando subgrafos que tienen un punto de entrada único y un punto de salida único, que luego se reemplazan por un solo nodo. Esta reducción corresponde a lo que haría un humano si extrajera una subrutina del código más grande. (Hoy en día, tal proceso caería bajo el término general de refactorización). El método de reducción de McCabe se llamó más tarde condensación en algunos libros de texto, porque se consideraba una generalización de la condensación a los componentes utilizados. en teoría de grafos. Si un programa está estructurado, entonces el proceso de reducción/condensación de McCabe lo reduce a un único nodo CFG. En cambio, si el programa no está estructurado, el proceso iterativo identificará la parte irreductible. La medida de complejidad esencial definida por McCabe es simplemente la complejidad ciclomática de este gráfico irreducible, por lo que será precisamente 1 para todos los programas estructurados, pero mayor que uno para los programas no estructurados.

Implicaciones para las pruebas de software

Otra aplicación de la complejidad ciclomática consiste en determinar el número de casos de prueba que son necesarios para lograr una cobertura completa de un módulo en particular.

Es útil debido a dos propiedades de la complejidad ciclomática, $M$ , para un módulo específico:

$M$ es un límite superior para el número de casos de prueba que son necesarios para lograr una cobertura de rama completa.
$M$ es un límite inferior para el número de caminos a través del gráfico de flujo de control (CFG). Asumiendo que cada caso de prueba tome un camino, el número de casos necesarios para alcanzar la cobertura del camino es igual al número de caminos que se pueden tomar. Pero algunos caminos pueden ser imposibles, por lo que aunque el número de caminos a través del CFG es claramente un límite superior en el número de casos de prueba necesarios para la cobertura del camino, este último número (de posible caminos) es a veces menos que $M$ .

Los tres números anteriores pueden ser iguales: cobertura de ramas ${displaystyle leq }$ complejidad ciclomática ${displaystyle leq }$ número de caminos.

Por ejemplo, considere un programa que consta de dos declaraciones secuenciales if-then-else.

si ()c1() f1();más f2();si ()c2() f3();más f4();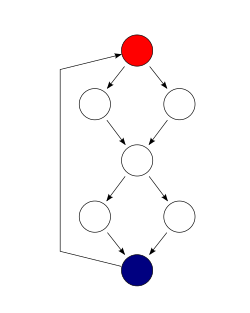

En este ejemplo, dos casos de prueba son suficientes para lograr una cobertura de rama completa, mientras que cuatro son necesarios para la cobertura completa de la ruta. La complejidad ciclomática del programa es 3 (como el gráfico fuertemente conectado para el programa contiene 9 bordes, 7 nodos y 1 componente conectado) ( $9 - 7 + 1$ ).

En general, para probar completamente un módulo, se deben ejercitar todas las rutas de ejecución a través del módulo. Esto implica que un módulo con un número de complejidad alto requiere más esfuerzo de prueba que un módulo con un valor más bajo, ya que el número de complejidad más alto indica más rutas a través del código. Esto también implica que un módulo con mayor complejidad es más difícil de entender para un programador, ya que el programador debe comprender las diferentes vías y los resultados de esas vías.

Desafortunadamente, no siempre es práctico probar todas las rutas posibles a través de un programa. Considerando el ejemplo anterior, cada vez que se agrega una declaración adicional if-then-else, el número de rutas posibles aumenta en un factor de 2. A medida que el programa crece de esta manera, rápidamente llega al punto en que probar todas las rutas se convierte en poco práctico.

Una estrategia de prueba común, adoptada por ejemplo por la metodología de pruebas estructuradas del NIST, es utilizar la complejidad ciclomática de un módulo para determinar la cantidad de pruebas de caja blanca que se requieren para obtener una cobertura suficiente del módulo. En casi todos los casos, según dicha metodología, un módulo debería tener al menos tantas pruebas como su complejidad ciclomática; en la mayoría de los casos, este número de pruebas es adecuado para ejercer todas las vías relevantes de la función.

Como ejemplo de una función que requiere más que simplemente cobertura de rama para realizar pruebas con precisión, considere nuevamente la función anterior, pero suponga que para evitar que ocurra un error, cualquier código que llame a f1() o f3() también debe llamar al otro. Suponiendo que los resultados de c1() y c2() son independientes, eso significa que la función presentada anteriormente contiene un error. La cobertura de sucursales nos permitiría probar el método con solo dos pruebas, y un posible conjunto de pruebas sería probar los siguientes casos:

c1() devuelve verdad y c2() retornos verdaderos
c1() devuelve falso y c2() devuelve falsos

Ninguno de estos casos expone el error. Sin embargo, si utilizamos la complejidad ciclomática para indicar el número de pruebas que requerimos, el número aumenta a 3. Por lo tanto, debemos probar una de las siguientes rutas:

c1() devuelve verdad y c2() devuelve falsos
c1() devuelve falso y c2() retornos verdaderos

Cualquiera de estos exámenes expondrá el fallo.

Correlación al número de defectos

Varios estudios han investigado la correlación entre el número de complejidad ciclomática de McCabe con la frecuencia de defectos que ocurren en una función o método. Algunos estudios encuentran una correlación positiva entre la complejidad ciclomática y los defectos: las funciones y métodos que tienen la mayor complejidad tienden a contener también la mayor cantidad de defectos. Sin embargo, la correlación entre la complejidad ciclomática y el tamaño del programa (normalmente medido en líneas de código) se ha demostrado muchas veces. Les Hatton ha afirmado que la complejidad tiene la misma capacidad predictiva que las líneas de código. Los estudios que controlaron el tamaño del programa (es decir, que compararon módulos que tienen diferentes complejidades pero tamaño similar) son generalmente menos concluyentes y muchos no encuentran correlación significativa, mientras que otros sí encuentran correlación. Algunos investigadores cuestionan la validez de los métodos utilizados en los estudios y no encuentran correlación. Aunque es probable que esta relación exista, no se utiliza fácilmente en la práctica. Dado que el tamaño del programa no es una característica controlable del software comercial, se ha cuestionado la utilidad del número de McCabe. La esencia de esta observación es que los programas más grandes tienden a ser más complejos y a tener más defectos. No se ha demostrado que reducir la complejidad ciclomática del código reduzca la cantidad de errores o errores en ese código. Sin embargo, los estándares de seguridad internacionales como ISO 26262 exigen pautas de codificación que imponen una baja complejidad del código.

Inteligencia artificial

La complejidad ciclomática también se puede utilizar para la evaluación de la complejidad semántica de programas de inteligencia artificial.

Topología ultramétrica

La complejidad ciclomática ha demostrado ser útil en el análisis geográfico y paisajístico-ecológico, después de que se demostró que puede implementarse en gráficos de distancias ultramétricas.

Más resultados...