Competencia Stackelberg

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Modelo económico

El modelo de liderazgo Stackelberg es un juego estratégico en economía en el que la empresa líder se mueve primero y luego las empresas seguidoras se mueven secuencialmente (de ahí que a veces se lo describa como el modelo de liderazgo “líder-seguidor”). juego"). Lleva el nombre del economista alemán Heinrich Freiherr von Stackelberg, que publicó Marktform und Gleichgewicht [Estructura y equilibrio del mercado] en 1934, en el que describía el modelo. En términos de teoría de juegos, los jugadores de este juego son un líder y un seguidor y compiten en cantidad. Al líder de Stackelberg a veces se le conoce como el líder del mercado.

Existen algunas limitaciones adicionales para el mantenimiento de un equilibrio de Stackelberg. El líder debe saber ex ante que el seguidor observa su acción. El seguidor no debe tener medios para comprometerse con la acción de un futuro líder que no sea Stackelberg y el líder debe saberlo. De hecho, si el 'seguidor' podría comprometerse con una acción del líder de Stackelberg y el 'líder' Sabía esto, la mejor respuesta del líder sería realizar una acción de seguidor de Stackelberg.

Las empresas pueden participar en la competencia de Stackelberg si una tiene algún tipo de ventaja que le permita avanzar primero. En términos más generales, el líder debe tener poder de compromiso. Actuar primero de manera observable es el medio más obvio de compromiso: una vez que el líder ha hecho su movimiento, no puede deshacerlo: está comprometido con esa acción. Pasar primero puede ser posible si el líder fuera el monopolio actual de la industria y el seguidor fuera un nuevo participante. Mantener el exceso de capacidad es otra forma de compromiso.

Equilibrio de Nash perfecto en subjuegos

El modelo de Stackelberg se puede resolver para encontrar el equilibrio o equilibrio de Nash perfecto en subjuegos (SPNE), es decir, el perfil de estrategia que mejor sirve a cada jugador, dadas las estrategias del otro jugador y que implica que cada jugador juegue en un equilibrio de Nash en cada subjuego.

En términos muy generales, que la función de precio para la industria (duopolio) sea ${displaystyle P}$ ; el precio es simplemente una función de la producción total (industria), así es ${displaystyle P(q_{1}+q_{2})}$ donde el subscript ${displaystyle _{1}}$ representa al líder y ${displaystyle _{2}}$ representa al seguidor. Suppose firm ${displaystyle i}$ tiene la estructura de costes ${displaystyle C_{i}(q_{i})}$ . El modelo se resuelve por inducción atrasada. El líder considera cuál es la mejor respuesta del seguidor, es decir, cómo es voluntad responder una vez que haya observado la cantidad del líder. El líder entonces elige una cantidad que maximiza su pago, anticipando la respuesta predicha del seguidor. El seguidor observa realmente esto y en equilibrio elige la cantidad esperada como respuesta.

Para calcular el SPNE, primero deben calcularse las mejores funciones de respuesta del seguidor (la cálculo se mueve hacia atrás debido a la inducción atrasada).

El beneficio de la firma ${displaystyle 2}$ (el seguidor) es el costo de los ingresos menos. Los ingresos son el producto del precio y la cantidad y el costo es dado por la estructura de costes de la firma, por lo que el beneficio es: ${displaystyle Pi _{2}=P(q_{1}+q_{2})cdot q_{2}-C_{2}(q_{2})}$ . La mejor respuesta es encontrar el valor de ${displaystyle q_{2}}$ que maximiza ${displaystyle Pi _{2}}$ dado ${displaystyle q_{1}}$ , es decir, dada la salida del líder (firma ${displaystyle 1}$ ), la salida que maximiza el beneficio del seguidor se encuentra. Por lo tanto, el máximo ${displaystyle Pi _{2}}$ con respecto a ${displaystyle q_{2}}$ es para ser encontrado. Primera diferencia ${displaystyle Pi _{2}}$ con respecto a ${displaystyle q_{2}}$ :

{displaystyle {frac {partial Pi _{2}}{partial q_{2}}}={frac {partial P(q_{1}+q_{2})}{partial q_{2}}}cdot q_{2}+P(q_{1}+q_{2})-{frac {partial C_{2}(q_{2})}{partial q_{2}}}.}

Establecer esto a cero para maximizar:

{displaystyle {frac {partial Pi _{2}}{partial q_{2}}}={frac {partial P(q_{1}+q_{2})}{partial q_{2}}}cdot q_{2}+P(q_{1}+q_{2})-{frac {partial C_{2}(q_{2})}{partial q_{2}}}=0.}

Los valores de ${displaystyle q_{2}}$ que satisfacen esta ecuación son las mejores respuestas. Ahora se considera la mejor función de respuesta del líder. Esta función se calcula considerando la salida del seguidor como función de la salida del líder, como acaba de computar.

El beneficio de la firma ${displaystyle 1}$ (el líder) es ${displaystyle Pi _{1}=P(q_{1}+q_{2}(q_{1})).q_{1}-C_{1}(q_{1})}$ , donde ${displaystyle q_{2}(q_{1})}$ es la cantidad del seguidor como función de la cantidad del líder, a saber, la función calculada arriba. La mejor respuesta es encontrar el valor de ${displaystyle q_{1}}$ que maximiza ${displaystyle Pi _{1}}$ dado ${displaystyle q_{2}(q_{1})}$ , es decir, dada la mejor función de respuesta del seguidor (firma ${displaystyle 2}$ ), la salida que maximiza el beneficio del líder se encuentra. Por lo tanto, el máximo ${displaystyle Pi _{1}}$ con respecto a ${displaystyle q_{1}}$ es para ser encontrado. Primero, diferenciar ${displaystyle Pi _{1}}$ con respecto a ${displaystyle q_{1}}$ :

{displaystyle {frac {partial Pi _{1}}{partial q_{1}}}={frac {partial P(q_{1}+q_{2})}{partial q_{2}}}cdot {frac {partial q_{2}(q_{1})}{partial q_{1}}}cdot q_{1}+{frac {partial P(q_{1}+q_{2})}{partial q_{1}}}cdot q_{1}+P(q_{1}+q_{2}(q_{1}))-{frac {partial C_{1}(q_{1})}{partial q_{1}}}.}

Estableciendo esto en cero para maximizar:

{displaystyle {frac {partial Pi _{1}}{partial q_{1}}}={frac {partial P(q_{1}+q_{2})}{partial q_{2}}}cdot {frac {partial q_{2}(q_{1})}{partial q_{1}}}cdot q_{1}+{frac {partial P(q_{1}+q_{2})}{partial q_{1}}}cdot q_{1}+P(q_{1}+q_{2}(q_{1}))-{frac {partial C_{1}(q_{1})}{partial q_{1}}}=0.}

Ejemplos

El siguiente ejemplo es muy general. Supone una estructura de demanda lineal generalizada.

{displaystyle p(q_{1}+q_{2})={bigg (}a-b(q_{1}+q_{2}){bigg)}}

e impone algunas restricciones a las estructuras de costos en aras de la simplicidad para que el problema pueda resolverse.

{displaystyle {frac {partial ^{2}C_{i}(q_{i})}{partial q_{i}cdot partial q_{j}}}=0,forall j}

{displaystyle {frac {partial C_{i}(q_{i})}{partial q_{j}}}=0,jneq i}

para facilitar el cálculo.

El beneficio del seguidor es:

{displaystyle pi _{2}={bigg (}a-b(q_{1}+q_{2}){bigg)}cdot q_{2}-C_{2}(q_{2}).}

El problema de maximización se resuelve a (del caso general):

{displaystyle {frac {partial {bigg (}a-b(q_{1}+q_{2}){bigg)}}{partial q_{2}}}cdot q_{2}+a-b(q_{1}+q_{2})-{frac {partial C_{2}(q_{2})}{partial q_{2}}}=0,}

{displaystyle Rightarrow -bq_{2}+a-b(q_{1}+q_{2})-{frac {partial C_{2}(q_{2})}{partial q_{2}}}=0,}

{displaystyle Rightarrow q_{2}={frac {a-bq_{1}-{frac {partial C_{2}(q_{2})}{partial q_{2}}}}{2b}}.}

Considere el problema del líder:

{displaystyle Pi _{1}={bigg (}a-b(q_{1}+q_{2}(q_{1})){bigg)}cdot q_{1}-C_{1}(q_{1}).}

Sustitución ${displaystyle q_{2}(q_{1})}$ del problema del seguidor:

{displaystyle Pi _{1}={bigg (}a-b{bigg (}q_{1}+{frac {a-bq_{1}-{frac {partial C_{2}(q_{2})}{partial q_{2}}}}{2b}}{bigg)}{bigg)}cdot q_{1}-C_{1}(q_{1}),}

{displaystyle Rightarrow Pi _{1}={bigg (}{frac {a-b.q_{1}+{frac {partial C_{2}(q_{2})}{partial q_{2}}}}{2}}){bigg)}cdot q_{1}-C_{1}(q_{1}).}

El problema de maximización se resuelve (desde el caso general):

{displaystyle {frac {partial pi _{1}}{partial q_{1}}}={bigg (}{frac {a-2bq_{1}+{frac {partial C_{2}(q_{2})}{partial q_{2}}}}{2}}{bigg)}-{frac {partial C_{1}(q_{1})}{partial q_{1}}}=0.}

Ahora resolviendo ${displaystyle q_{1}}$ rendimientos ${displaystyle q_{1}^{*}}$ , la acción óptima del líder:

{displaystyle q_{1}^{*}={frac {a+{frac {partial C_{2}(q_{2})}{partial q_{2}}}-2cdot {frac {partial C_{1}(q_{1})}{partial q_{1}}}}{2b}}.}

Esta es la mejor respuesta del líder a la reacción del seguidor en equilibrio. Ahora se puede encontrar el seguimiento alimentando esto en su función de reacción calculada anteriormente:

{displaystyle q_{2}^{*}={frac {a-bcdot {frac {a+{frac {partial C_{2}(q_{2})}{partial q_{2}}}-2cdot {frac {partial C_{1}(q_{1})}{partial q_{1}}}}{2b}}-{frac {partial C_{2}(q_{2})}{partial q_{2}}}}{2b}},}

{displaystyle Rightarrow q_{2}^{*}={frac {a-3cdot {frac {partial C_{2}(q_{2})}{partial q_{2}}}+2cdot {frac {partial C_{1}(q_{1})}{partial q_{1}}}}{4b}}.}

Los equilibrios de Nash son todos ${displaystyle (q_{1}^{*},q_{2}^{*})}$ . Está claro (si se supone que los costos marginales son cero - es decir, el costo es esencialmente ignorado) que el líder tiene una ventaja significativa. Intuitivamente, si el líder no fuera mejor que el seguidor, simplemente adoptaría una estrategia de competencia de Cournot.

Enchufar la cantidad del seguidor ${displaystyle q_{2}}$ , volver a la mejor función de respuesta del líder no cederá ${displaystyle q_{1}}$ . Esto se debe a que una vez que el líder se ha comprometido con una salida y observó a los seguidores que siempre quiere reducir su salida ex-post. Sin embargo, su incapacidad para hacerlo es lo que le permite recibir mayores ganancias que bajo Cournot.

Análisis económico

A menudo se utiliza una representación de forma extensiva para analizar el modelo líder-seguidor de Stackelberg. También conocido como “árbol de decisión”, el modelo muestra la combinación de productos y beneficios que ambas empresas tienen en el juego de Stackelberg.

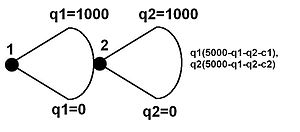
La imagen de la izquierda muestra de forma extensa un juego de Stackelberg. Los pagos se muestran a la derecha. Este ejemplo es bastante simple. Existe una estructura de costos básica que involucra sólo costos marginales (no hay costos fijos). La función de demanda es lineal y la elasticidad precio de la demanda es 1. Sin embargo, ilustra la ventaja del líder.

El seguidor quiere elegir ${displaystyle q_{2}}$ para maximizar su pago ${displaystyle q_{2}times (5000-q_{1}-q_{2}-c_{2})}$ . Tomar el primer orden derivado y equipararlo a cero (para maximizar) rendimientos ${displaystyle q_{2}={frac {5000-q_{1}-c_{2}}{2}}}$ como el valor máximo ${displaystyle q_{2}}$ .

El líder quiere elegir ${displaystyle q_{1}}$ para maximizar su pago ${displaystyle q_{1}times (5000-q_{1}-q_{2}-c_{1})}$ . Sin embargo, en equilibrio, sabe que el seguidor elegirá ${displaystyle q_{2}}$ como arriba. Así que de hecho el líder quiere maximizar su pago ${displaystyle q_{1}times (5000-q_{1}-{frac {5000-q_{1}-c_{2}}{2}}-c_{1})}$ (por sustitución ${displaystyle q_{2}}$ para la mejor función de respuesta del seguidor). Por diferenciación, el pago máximo es dado por ${displaystyle q_{1}={frac {5000-2c_{1}+c_{2}}{2}}}$ . Alimentar esto en los mejores rendimientos de la función de respuesta del seguidor ${displaystyle q_{2}={frac {5000+2c_{1}-3c_{2}}{4}}}$ . Supongamos que los costos marginales eran iguales para las empresas (por lo que el líder no tiene ninguna ventaja de mercado aparte de la primera jugada) y en particular ${displaystyle c_{1}=c_{2}=1000}$ . El líder produciría 2000 y el seguidor produciría 1000. Esto daría al líder un beneficio (pago) de dos millones y al seguidor un beneficio de un millón. Simplemente moviéndose primero, el líder ha acumulado dos veces el beneficio del seguidor. Sin embargo, las ganancias de Cournot aquí son 1.78 millones de piezas (strictamente, ${displaystyle (16/9)10^{6}}$ apiece), por lo que el líder no ha ganado mucho, pero el seguidor ha perdido. Sin embargo, esto es un ejemplo específico. Puede haber casos en que un líder de Stackelberg tiene enormes ganancias más allá de las ganancias de Cournot que se acercan a los beneficios monopolísticos (por ejemplo, si el líder también tenía una gran ventaja de la estructura de costos, quizás debido a una mejor función de producción). También puede haber casos en que el seguidor realmente disfruta de mayores ganancias que el líder, pero sólo porque, por ejemplo, tiene costos mucho más bajos. Este comportamiento trabaja constantemente en mercados de duopolio, incluso si las empresas son asimétricas.

Amenazas creíbles y no creíbles por parte del seguidor

Si, después de que el líder hubiera seleccionado su cantidad de equilibrio, el seguidor se desviara del equilibrio y eligiera alguna cantidad no óptima, no sólo se perjudicaría a sí mismo, sino que también podría perjudicar al líder. Si el seguidor eligiera una cantidad mucho mayor que su mejor respuesta, el precio de mercado bajaría y las ganancias del líder se verían perjudicadas, tal vez por debajo de las ganancias del nivel de Cournot. En este caso, el seguidor podría anunciar al líder antes de que comience el juego que, a menos que el líder elija una cantidad de equilibrio de Cournot, el seguidor elegirá una cantidad desviada que afectará las ganancias del líder. Después de todo, la cantidad elegida por el líder en equilibrio sólo es óptima si el seguidor también juega en equilibrio. El líder, sin embargo, no corre peligro. Una vez que el líder ha elegido su cantidad de equilibrio, sería irracional que el seguidor se desviara porque él también resultaría perjudicado. Una vez que el líder ha elegido, al seguidor le irá mejor si sigue el camino del equilibrio. Por lo tanto, tal amenaza por parte del seguidor no sería creíble.

Sin embargo, en un juego de Stackelberg repetido (indefinidamente), el seguidor podría adoptar una estrategia de castigo en la que amenaza con castigar al líder en el siguiente período a menos que elija una estrategia no óptima en el período actual. Esta amenaza puede ser creíble porque podría ser racional que el seguidor castigue en el siguiente periodo de manera que el líder elija cantidades de Cournot a partir de entonces.

Stackelberg comparado con Cournot

Los modelos Stackelberg y Cournot son similares porque en ambos la competencia es en cantidad. Sin embargo, como se ve, el primer movimiento le da al líder de Stackelberg una ventaja crucial. También existe el importante supuesto de información perfecta en el juego de Stackelberg: el seguidor debe observar la cantidad elegida por el líder; de lo contrario, el juego se reduce a Cournot. Con información imperfecta, las amenazas descritas anteriormente pueden ser creíbles. Si el seguidor no puede observar el movimiento del líder, ya no es irracional que elija, digamos, un nivel de cantidad de Cournot (de hecho, esa es la acción de equilibrio). Sin embargo, debe ser que hay información imperfecta y el seguidor es incapaz de observar el movimiento del líder porque es irracional que el seguidor no observe si puede una vez que el líder se ha movido. Si puede observar, lo hará para poder tomar la decisión óptima. Cualquier amenaza por parte del seguidor afirmando que no observará aunque pueda hacerlo es tan increíble como las anteriores. Este es un ejemplo de cómo demasiada información perjudica a un jugador. En la competición de Cournot, es la simultaneidad del juego (la imperfección del conocimiento) lo que da como resultado que ninguno de los jugadores (ceteris paribus) esté en desventaja.

Consideraciones teóricas del juego

Como se mencionó, la información imperfecta en un juego de liderazgo se reduce a la competencia de Cournot. Sin embargo, algunos perfiles de estrategias de Cournot se mantienen como equilibrios de Nash, pero pueden eliminarse como amenazas increíbles (como se describió anteriormente) aplicando el concepto de solución de perfección en subjuegos. De hecho, es precisamente lo que hace que una estrategia de Cournot perfile un equilibrio de Nash en un juego de Stackelberg lo que le impide ser perfecto en subjuegos.

Considere un juego Stackelberg (es decir, uno que cumple con los requisitos descritos anteriormente para sostener un equilibrio Stackelberg) en el que, por alguna razón, el líder cree que cualquier acción que tome, el seguidor elegirá una cantidad de Cournot (tal vez el líder cree que el seguidor es irracional). Si el líder jugó una acción de Stackelberg, (cree) que el seguidor jugará Cournot. Por lo tanto no es optimista para el líder jugar Stackelberg. De hecho, su mejor respuesta (por la definición de equilibrio de Cournot) es jugar la cantidad de Cournot. Una vez hecho esto, la mejor respuesta del seguidor es jugar Cournot.

Considere los siguientes perfiles de estrategia: el líder juega Cournot; el seguidor juega Cournot si el líder juega Cournot y el seguidor juega Stackelberg si el líder juega Stackelberg y si el líder juega algo más, el seguidor juega una estrategia arbitraria (de ahí que esto realmente describe varios perfiles). Este perfil es un equilibrio de Nash. Como se ha dicho anteriormente, en el camino del equilibrio el juego es una mejor respuesta a una mejor respuesta. Sin embargo, jugar Cournot no habría sido la mejor respuesta del líder si el seguidor jugaría Stackelberg si (el líder) jugara Stackelberg. En este caso, la mejor respuesta del líder sería jugar a Stackelberg. Por lo tanto, lo que hace este perfil (o más bien, estos perfiles) un equilibrio Nash (o más bien, Nash equilibria) es el hecho de que el seguidor jugaría no-Stackelberg si el líder fuera a jugar Stackelberg.

Sin embargo, este mismo hecho (que el seguidor jugaría no-Stackelberg si el líder jugara Stackelberg) significa que este perfil no es un equilibrio de Nash del subjuego que comienza cuando el líder ya jugó Stackelberg (un subjuego fuera del camino de equilibrio). Si el líder ya jugó Stackelberg, la mejor respuesta del seguidor es jugar Stackelberg (y por lo tanto es la única acción que produce un equilibrio de Nash en este subjuego). Por lo tanto, el perfil de estrategia, que es Cournot, no es perfecto en subjuegos.

Comparación con otros modelos de oligopolio

En comparación con otros modelos de oligopolio,

La salida agregada Stackelberg es mayor que la salida agregada Cournot, pero menos que la salida agregada Bertrand.
El precio de Stackelberg es inferior al precio Cournot, pero mayor que el precio de Bertrand.
El excedente de consumo de Stackelberg es mayor que el excedente de consumo de Cournot, pero inferior al excedente de consumo de Bertrand.
La producción agregada de Stackelberg es mayor que el monopolio o cártel puro, pero menos que la salida perfectamente competitiva.
El precio de Stackelberg es menor que el monopolio puro o el precio del cártel, pero mayor que el precio perfectamente competitivo.

Aplicaciones

El concepto Stackelberg se ha extendido a los juegos dinámicos Stackelberg. Con la incorporación del tiempo como dimensión, se descubrieron fenómenos que no se encuentran en los juegos estáticos, como la violación del principio de optimización por parte del líder.

En los últimos años, los juegos de Stackelberg se han aplicado en el ámbito de la seguridad. En este contexto, el defensor (líder) diseña una estrategia para proteger un recurso, de modo que el recurso permanezca seguro independientemente de la estrategia adoptada por el atacante (seguidor). Los juegos diferenciales de Stackelberg también se utilizan para modelar cadenas de suministro y canales de marketing. Otras aplicaciones de los juegos de Stackelberg incluyen redes heterogéneas, privacidad genética, robótica, conducción autónoma, redes eléctricas y sistemas energéticos integrados.