Comparación de sistemas electorales
Los sistemas electorales son las reglas para llevar a cabo las elecciones, un componente principal de los cuales es el algoritmo para determinar el ganador (o varios ganadores) a partir de las papeletas emitidas. Este artículo analiza los métodos y resultados de la comparación de diferentes sistemas electorales, tanto aquellos que eligen a un solo candidato en una elección de 'ganador único' como aquellos que eligen a un grupo de representantes en una elección de múltiples ganadores.
Hay 3 tipos principales de razonamiento que se han utilizado para tratar de determinar el mejor método de votación:
- Argumento por ejemplo
- Adhesión a criterios lógicos
- Resultados de elecciones simuladas
Opiniones de expertos
En 2010, se preguntó a un panel de 22 expertos en procedimientos de votación: "¿Cuál es la mejor regla de votación que puede usar su ciudad para elegir al alcalde?". Un miembro se abstuvo. La votación de aprobación se utilizó para decidir entre 18 métodos de votación de un solo ganador. La clasificación (con número N de aprobadores de un máximo de 21) de los distintos sistemas fue la siguiente.
Nota: esta lista no es representativa de todos los métodos de votación de un solo ganador disponibles, y varios de los expertos involucrados notaron fallas en la forma en que se realizó la encuesta. El organizador de la encuesta argumenta que los resultados no deben generalizarse, refiriéndose a ella como un "voto ingenuo sobre las reglas de votación".
| Posición | Método | norte |
|---|---|---|
| 1 | Votación de aprobación | 15 |
| 2 | Voto alternativo (IRV) | 10 |
| 3 | método de Copeland | 9 |
| 4 | Método Kemeny-Young | 8 |
| 5 | Sistema de dos vueltas | 6 |
| 5 | método de Coombs | 6 |
| 7 | minimax | 5 |
| 7 | Juicio mayoritario | 5 |
| 9 | cuenta borde | 4 |
| 10 | método de negro | 3 |
| 11 | Rango de votación | 2 |
| 11 | método de nanson | 2 |
| 13 | método de leximina | 1 |
| 13 | método de smith | 1 |
| 13 | Método de conjunto descubierto | 1 |
| dieciséis | método de fishburn | – |
| dieciséis | Conjunto sin atrapar | – |
| dieciséis | FPTP | – |
Consideraciones pragmáticas
Un problema intelectual planteado por la teoría del voto es el de diseñar sistemas que sean precisos en algún sentido. Sin embargo, también existen razones prácticas por las que un sistema puede ser más aceptable socialmente que otro.
Los factores importantes se pueden agrupar en 3 encabezados:
- Inteligibilidad, que Tideman define como "la capacidad de la regla para ganarse la confianza de los votantes" y "depende de la razonabilidad y comprensibilidad de la lógica de la regla".
- Facilidad de votar. Las diferentes formas de votación hacen que sea más o menos difícil para los votantes completar las papeletas que reflejen sus puntos de vista de manera justa.
- Facilidad de contar. Los sistemas de votación que pueden tomar sus decisiones a partir de un pequeño conjunto de conteos derivados de las boletas son logísticamente menos onerosos que aquellos que necesitan consultar todo el conjunto de boletas. Algunos sistemas de votación requieren poderosos recursos computacionales para determinar el ganador. Incluso si el costo no es prohibitivo para uso electoral, puede impedir una evaluación efectiva.
Efectos de la candidatura
Un tema aparte es el hecho de que se puede alentar a diferentes candidatos a presentarse a las elecciones bajo diferentes sistemas de votación. El miedo a los votos desperdiciados bajo el FPTP pone mucho poder en manos de los grupos que seleccionan a los candidatos. Un sistema de votación diferente podría conducir a decisiones más satisfactorias sin ser necesariamente más justo en ningún sentido abstracto. Este tema ha recibido poco estudio analítico.
Evaluación por simulación
Modelos del proceso electoral
Los métodos de votación se pueden evaluar midiendo su precisión en elecciones aleatorias simuladas con el objetivo de ser fieles a las propiedades de las elecciones en la vida real. La primera evaluación de este tipo fue realizada por Chamberlin y Cohen en 1978, quienes midieron la frecuencia con la que ciertos sistemas que no eran de Condorcet elegían a los ganadores de Condorcet. Hay tres tipos principales de modelos que se han propuesto como representaciones del proceso electoral, dos de los cuales se pueden combinar en un híbrido. Un cuarto tipo de modelo, el modelo utilitario, es de importancia conceptual a pesar de no ser utilizado en la práctica, aunque los modelos espaciales a veces se presentan en forma utilitaria.
Modelo de jurado de Condorcet
El marqués de Condorcet veía una elección como análoga a una votación del jurado en la que cada miembro expresa un juicio independiente sobre la calidad de los candidatos. Por esta razón, los candidatos difieren en mérito objetivo y los electores expresan puntos de vista independientes sobre los méritos relativos de los candidatos. Mientras los juicios de los votantes sean mejores que aleatorios, un electorado suficientemente grande siempre elegirá al mejor candidato. Un modelo de jurado a veces se conoce como modelo de valencia.
El modelo de jurado implica un concepto natural de precisión para los sistemas de votación: cuanto más probable sea un sistema para elegir al mejor candidato, mejor será el sistema. Esto puede verse como una semántica para las decisiones electorales.
Condorcet y su contemporáneo Laplace se dieron cuenta de que la teoría del voto podía reducirse a la teoría de la probabilidad: el trabajo principal de Condorcet se tituló Essai sur l'application de l'analyse à la probabilité des décisions rendues à la pluralité des voix. Sus ideas fueron revividas en el siglo XX cuando se demostró bajo un modelo de jurado que el método de votación de Kemeny-Young es el estimador de máxima verosimilitud de la ordenación de candidatos por mérito.
Modelo espacial de Black
La principal debilidad del modelo de Condorcet es su suposición de independencia: implica que no puede haber una tendencia a que los votantes que prefieren A a B prefieran también C a D. Esto va en contra de la evidencia: alguien que prefiere cierto montagnard a un cierto girondin probablemente también preferirá un segundo montagnard a un segundo girondin; también explica por qué incluso los jurados arbitrariamente grandes son falibles, ya que los miembros cometerán errores comunes.
Duncan Black propuso un modelo espacial unidimensional de votación en 1948, considerando las elecciones como impulsadas ideológicamente. Sus ideas fueron posteriormente ampliadas por Anthony Downs. Las opiniones de los votantes se consideran posiciones en un espacio de una o más dimensiones; los candidatos tienen posiciones en el mismo espacio; y los votantes eligen a los candidatos en orden de proximidad (medida bajo la distancia euclidiana o alguna otra métrica).
Los modelos espaciales implican una noción diferente de mérito para los sistemas de votación: cuanto más aceptable sea el candidato ganador como parámetro de ubicación para la distribución de votantes, mejor será el sistema. Un espectro político es un modelo espacial unidimensional.
Modelo neutral de Arrow
Kenneth Arrow trabajó dentro de un marco en el que las papeletas son la realidad última en lugar de ser 'mensajes' (como lo expresaron Balinski y Laraki ) que transmiten información parcial (y posiblemente engañosa) sobre alguna realidad detrás de ellos. No propuso este agnosticismo como una imagen realista de la votación, sino más bien como una definición de las elecciones como objetos matemáticos cuyas propiedades podrían investigarse. Su famoso teorema de la imposibilidad muestra (bajo ciertos supuestos) que para cualquier sistema de votación clasificado, existen conjuntos de boletas (obtenibles bajo un modelo neutral) que violan al menos uno de los tres criterios que a menudo se consideran deseables.
Un modelo neutral no trae consigo ningún concepto de precisión o verdad para los sistemas de votación.
Los modelos de cultura imparcial definen las distribuciones de los votos emitidos bajo un modelo de votación neutral, que trata al electorado como una fuente aleatoria de ruido.
Modelos híbridos
Es posible combinar modelos de jurado con modelos espaciales: se puede suponer que los votantes están influenciados en parte por sus puntos de vista sobre las cualidades de los candidatos y en parte por consideraciones ideológicas. Esto desglosa sus preferencias en componentes separados independientes y no independientes. Darlington analiza brevemente los modelos híbridos, pero no se han adoptado ampliamente.
Comparación empírica
Tideman y Plassmann realizaron un estudio que mostró que un modelo espacial bidimensional proporcionaba un ajuste razonable a las reducciones de 3 candidatos de un gran conjunto de clasificaciones electorales. Se demostró que los modelos jurado y neutral y los modelos espaciales unidimensionales eran inadecuados, pero no se consideraron los modelos híbridos.
Examinaron los ciclos de Condorcet en las preferencias de los votantes (un ejemplo de lo cual es que A es preferido a B por la mayoría de los votantes, B a C y C a A) y encontraron que el número de ellos era consistente con los efectos de muestra pequeña, concluyendo que "los ciclos de votación ocurrirán muy raramente, si es que ocurren, en elecciones con muchos votantes".
La relevancia del tamaño de la muestra había sido estudiada previamente por Gordon Tullock, quien argumentó gráficamente que aunque los electores finitos siempre serán propensos a los ciclos, el área en la que los candidatos pueden generar ciclos se vuelve progresivamente más pequeña a medida que aumenta el número de votantes.
Modelos utilitarios
Un modelo utilitario ve a los votantes como candidatos clasificados en orden de utilidad. El ganador legítimo, según este modelo, es el candidato que maximiza la utilidad social general. Un modelo utilitario se diferencia de un modelo espacial en varios aspectos importantes:
- Requiere la suposición adicional de que los votantes están motivados únicamente por un interés propio informado, sin ninguna mancha ideológica en sus preferencias.
- Requiere que la métrica de distancia de un modelo espacial sea reemplazada por una medida fiel de utilidad.
- En consecuencia, la métrica deberá diferir entre los votantes. A menudo sucede que un grupo de votantes se verá fuertemente afectado por la elección entre dos candidatos mientras que otro grupo tiene poco en juego; la métrica entonces necesitará ser altamente asimétrica.
De la última propiedad se deduce que ningún sistema de votación que otorgue la misma influencia a todos los votantes es probable que logre la máxima utilidad social. Los casos extremos de conflicto entre las pretensiones del utilitarismo y la democracia se denominan "tiranía de la mayoría". Ver los comentarios de Laslier, Merlin y Nurmi en el artículo de Laslier.
James Mill parece haber sido el primero en afirmar la existencia de una conexión a priori entre la democracia y el utilitarismo – ver el artículo de la Enciclopedia de Stanford y el 'famoso ataque' de Macaulay.
Comparaciones bajo un modelo de jurado
Supongamos que el candidato i en una elección tiene un mérito x i (podemos suponer que x i ~ N (0,σ)), y que el nivel de aprobación del votante j para el candidato i puede escribirse como x i + ε ij (supondremos que los ε ij son iid.N (0,τ )). Suponemos que un votante clasifica a los candidatos en orden decreciente de aprobación. Podemos interpretar ε ij como el error en la valoración del candidato i por parte del votante jy considerar que un método de votación tiene la tarea de encontrar al candidato de mayor mérito.
Cada votante clasificará al mejor de dos candidatos por encima del menos bueno con una determinada probabilidad p (que bajo el modelo normal descrito aquí es igual a 
Peyton Young demostró que se aplican otras tres propiedades a los votos entre números arbitrarios de candidatos, lo que sugiere que Condorcet conocía la primera y la tercera.
- Si p está cerca de 1 ⁄ 2, entonces el ganador de Borda es el estimador de máxima verosimilitud del mejor candidato.
- si p está cerca de 1, entonces el ganador Minimax es el estimador de máxima verosimilitud del mejor candidato.
- Para cualquier p, la clasificación de Kemeny-Young es el estimador de máxima verosimilitud del verdadero orden de mérito.
Robert F. Bordley construyó un modelo "utilitario" que es una ligera variante del modelo del jurado de Condorcet. Consideró que la tarea de un método de votación es encontrar al candidato que tenga la mayor aprobación total del electorado, es decir, la suma más alta de los niveles de aprobación de los votantes individuales. Este modelo tiene sentido incluso con σ = 0, en cuyo caso p toma el valor 
Elecciones simuladas bajo modelos espaciales
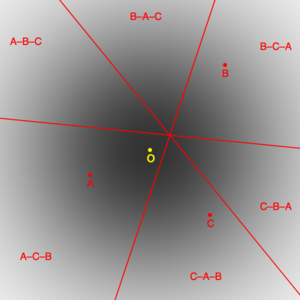
Una elección simulada se puede construir a partir de una distribución de votantes en un espacio adecuado. La ilustración muestra votantes que satisfacen una distribución gaussiana bivariada centrada en O. Hay 3 candidatos generados aleatoriamente, A, B y C. El espacio está dividido en 6 segmentos por 3 líneas, y los votantes de cada segmento tienen las mismas preferencias de candidatos. La proporción de votantes que ordenan a los candidatos de alguna forma viene dada por la integral de la distribución de votantes sobre el segmento asociado.
Las proporciones correspondientes a los 6 ordenamientos posibles de candidatos determinan los resultados arrojados por los diferentes sistemas de votación. Las que eligen al mejor candidato, es decir, el candidato más cercano a O (que en este caso es A), se considera que han dado un resultado correcto, y las que eligen a otra persona han presentado un error. Al observar los resultados de un gran número de candidatos generados aleatoriamente, se pueden medir las propiedades empíricas de los sistemas de votación.
El protocolo de evaluación descrito aquí se basa en el descrito por Tideman y Plassmann. Las evaluaciones de este tipo son más comunes para los sistemas electorales de un solo ganador. Los sistemas de votación clasificados encajan más naturalmente en el marco, pero otros tipos de papeletas (como FPTP y votación de aprobación) se pueden acomodar con mayor o menor esfuerzo.
El protocolo de evaluación se puede variar de varias maneras:
- El número de votantes se puede hacer finito y variar en tamaño. En la práctica, esto casi siempre se hace en modelos multivariados, en los que se muestrea a los votantes a partir de su distribución y se utilizan los resultados de grandes electorados para mostrar el comportamiento limitante.
- El número de candidatos puede ser variado.
- La distribución de votantes podría ser variada; por ejemplo, podría examinarse el efecto de las distribuciones asimétricas. Los efectos de muestreo aleatorio implican una pequeña desviación de la normalidad cuando el número de votantes es finito. Jameson Quinn investigó desviaciones más sistemáticas (que aparentemente toman la forma de un modelo de mezcla gaussiana) en 2017.
Evaluación de precisión
| metrométodo | 3 | 6 | 10 | 15 | 25 | 40 |
|---|---|---|---|---|---|---|
| FPTP | 70.6 | 35.5 | 21.1 | 14.5 | 9.3 | 6.4 |
| AV/VIR | 85.2 | 50.1 | 31.5 | 21.6 | 12.9 | 7.9 |
| Borda | 87.6 | 82.1 | 74.2 | 67.0 | 58.3 | 50.1 |
| Condorcet | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 |
Uno de los principales usos de las evaluaciones es comparar la precisión de los sistemas de votación cuando los votantes votan con sinceridad. Si un número infinito de votantes satisface una distribución gaussiana, entonces se puede considerar que el ganador legítimo de una elección es el candidato más cercano a la media/mediana, y la precisión de un método se puede identificar con la proporción de elecciones en las que el ganador legítimo se elige ganador. El teorema del votante mediano garantiza que todos los sistemas de Condorcet darán un 100% de precisión (y lo mismo se aplica al método de Coombs).
Las evaluaciones publicadas en trabajos de investigación utilizan gaussianas multidimensionales, lo que dificulta el cálculo numéricamente. El número de votantes se mantiene finito y el número de candidatos es necesariamente pequeño.
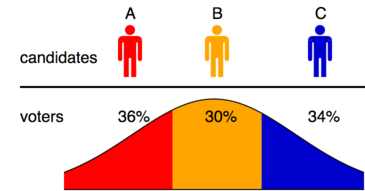
El cálculo es mucho más sencillo en una sola dimensión, lo que permite un número infinito de votantes y un número arbitrario m de candidatos. Los resultados de este caso simple se muestran en la primera tabla, que es directamente comparable con la Tabla 5 (1000 votantes, dispersión media) del artículo citado de Chamberlin y Cohen. Los candidatos se muestrearon aleatoriamente de la distribución de votantes y se incluyó un solo método de Condorcet (Minimax) en los ensayos para su confirmación.
| metrométodo | 10 |
|---|---|
| FPTP | 0.166 |
| AV/VIR | 0.058 |
| Borda | 0.016 |
| Condorcet | 0.010 |
El desempeño relativamente pobre del Voto Alternativo (IRV) se explica por la conocida y común fuente de error ilustrada por el diagrama, en el cual la elección satisface un modelo espacial univariado y el ganador legítimo B será eliminado en la primera vuelta. Un problema similar existe en todas las dimensiones.
Una medida alternativa de precisión es la distancia promedio de los votantes del ganador (en la que más pequeño significa mejor). Es poco probable que esto cambie la clasificación de los métodos de votación, pero lo prefieren las personas que interpretan la distancia como una desutilidad. La segunda tabla muestra la distancia promedio (en desviaciones estándar) menos 
Evaluación de la resistencia al voto táctico
James Green-Armytage et al. publicaron un estudio en el que evaluaron la vulnerabilidad de varios sistemas de votación a la manipulación por parte de los votantes. Dicen poco sobre cómo adaptaron su evaluación para este propósito, mencionando simplemente que 'requiere una programación creativa'. Un artículo anterior del primer autor da un poco más de detalle.
El número de candidatos en sus elecciones simuladas se limitó a 3. Esto elimina la distinción entre ciertos sistemas; por ejemplo, el método de Black y el método de Dasgupta-Maskin son equivalentes en 3 candidatos.
Las conclusiones del estudio son difíciles de resumir, pero el conteo de Borda tuvo un mal desempeño; Minimax era algo vulnerable; y IRV fue altamente resistente. Los autores demostraron que limitar cualquier método a elecciones sin ganador de Condorcet (elegir el ganador de Condorcet cuando lo hubiera) nunca aumentaría su susceptibilidad a la votación táctica. Informaron que el sistema 'Condorcet-Hare' que usa IRV como desempate para elecciones no resueltas por el criterio de Condorcet era tan resistente a la votación táctica como IRV por sí solo y más preciso. Condorcet-Hare es equivalente al método de Copeland con un desempate IRV en elecciones con 3 candidatos.
Evaluación del efecto de la distribución de candidatos
| Xmetro | 0 | 0.25 | 0.5 | 1 | 1.5 |
|---|---|---|---|---|---|
| 3 | 87.6 | 87,9 | 88,9 | 93.0 | 97.4 |
| 6 | 82.1 | 80.2 | 76.2 | 71,9 | 79,9 |
| 10 | 74.1 | 70.1 | 61.2 | 47.6 | 54.1 |
| 15 | 66,9 | 60.6 | 46.4 | 26.6 | 30.8 |
| 25 | 58.3 | 47.0 | 26.3 | 8.1 | 10.1 |
| 40 | 50.2 | 33.3 | 11.3 | 1.5 | 2.1 |
Algunos sistemas, y el conteo de Borda en particular, son vulnerables cuando la distribución de candidatos se desplaza en relación con la distribución de votantes. La tabla adjunta muestra la precisión del conteo de Borda (como porcentaje) cuando una población infinita de votantes satisface una distribución gaussiana univariada y se extraen m candidatos de una distribución similar compensada por x distribuciones estándar. La coloración roja indica cifras que son peores que aleatorias. Recuerde que todos los métodos de Condorcet dan una precisión del 100 % para este problema. (Y observe que la reducción en la precisión a medida que aumenta x no se ve cuando solo hay 3 candidatos).
La sensibilidad a la distribución de candidatos se puede considerar como una cuestión de precisión o de resistencia a la manipulación. Si uno espera que, en el curso de las cosas, los candidatos provengan naturalmente de la misma distribución que los votantes, entonces cualquier desplazamiento será visto como un intento de subversión; pero si uno piensa que los factores que determinan la viabilidad de la candidatura (como el respaldo financiero) pueden estar correlacionados con la posición ideológica, entonces lo verá más en términos de precisión.
Las evaluaciones publicadas toman diferentes puntos de vista de la distribución de candidatos. Algunos simplemente asumen que los candidatos provienen de la misma distribución que los votantes. Varios periódicos antiguos asumen medios iguales pero permiten que la distribución de candidatos sea más o menos ajustada que la distribución de votantes. Un artículo de Tideman y Plassmann aproxima la relación entre las distribuciones de candidatos y votantes basándose en mediciones empíricas.Esto es menos realista de lo que parece, ya que no permite que la distribución de candidatos se ajuste para explotar cualquier debilidad en el sistema de votación. Un artículo de James Green-Armytage analiza la distribución de candidatos como un tema separado, viéndolo como una forma de manipulación y midiendo los efectos de la entrada y salida estratégica. Como era de esperar, encuentra que el conde de Borda es particularmente vulnerable.
Evaluación para otras propiedades
- Como se mencionó anteriormente, Chamberlin y Cohen midieron la frecuencia con la que ciertos sistemas que no son de Condorcet eligen a los ganadores de Condorcet. Bajo un modelo espacial con distribuciones iguales de votantes y candidatos, las frecuencias son 99% (Coombs), 86% (Borda), 60% (IRV) y 33% (FPTP). Esto a veces se conoce como eficiencia de Condorcet.
- Darlington midió la frecuencia con la que el método de Copeland produce un único ganador en elecciones sin ganador Condorcet. Encontró que era menos del 50% para campos de hasta 10 candidatos.
Métricas experimentales
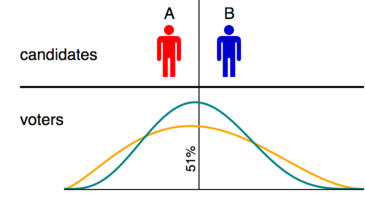
La tarea de un sistema de votación bajo un modelo espacial es identificar al candidato cuya posición representa con mayor precisión la distribución de las opiniones de los votantes. Esto equivale a elegir un parámetro de ubicación para la distribución del conjunto de alternativas que ofrecen los candidatos. Los parámetros de ubicación pueden basarse en la media, la mediana o la moda; pero dado que las boletas de preferencia clasificadas brindan solo información ordinal, la mediana es la única estadística aceptable.
Esto se puede ver en el diagrama, que ilustra dos elecciones simuladas con los mismos candidatos pero diferentes distribuciones de votantes. En ambos casos el punto medio entre los candidatos es el percentil 51 de la distribución de votantes; por lo tanto, el 51% de los votantes prefiere A y el 49% prefiere B. Si consideramos que un método de votación es correcto si elige al candidato más cercano a la mediana de la población de votantes, entonces, dado que la mediana está necesariamente ligeramente a la izquierda del 51% línea, un método de votación se considerará correcto si elige A en cada caso.
La media de la distribución verde azulado también está ligeramente a la izquierda de la línea del 51 %, pero la media de la distribución naranja está ligeramente a la derecha. Por lo tanto, si consideramos que un método de votación es correcto si elige al candidato más cercano a la media de la población de votantes, entonces un método no podrá obtener la máxima puntuación a menos que produzca diferentes ganadores de las mismas papeletas en las dos elecciones. Claramente, esto imputará errores espurios a los métodos de votación. El mismo problema surgirá para cualquier medida cardinal de ubicación; sólo la mediana da resultados consistentes.
La mediana no está definida para distribuciones multivariadas, pero la mediana univariada tiene una propiedad que se generaliza convenientemente. La mediana de una distribución es la posición cuya distancia promedio desde todos los puntos dentro de la distribución es la más pequeña. Esta definición se generaliza a la mediana geométrica en múltiples dimensiones. La distancia se describe a veces como la "desutilidad" de un votante de la elección de un candidato, pero esta identificación es puramente arbitraria.
Si tenemos un conjunto de candidatos y una población de votantes, entonces no es necesario resolver el difícil problema computacional de encontrar la mediana geométrica de los votantes y luego identificar al candidato más cercano a ella; en cambio, podemos identificar al candidato cuya distancia promedio de los votantes se minimiza. Esta es la métrica que se ha implementado generalmente desde Merrill en adelante; véase también Green-Armytage y Darlington.
El candidato más cercano a la mediana geométrica de la distribución de votantes puede denominarse "ganador espacial".
Argumento por ejemplo
| Número de votantes | Clasificación |
|---|---|
| 30 | A B C |
| 1 | ACB |
| 29 | BAC |
| 10 | BCA |
| 10 | TAXI |
| 1 | CBA |
Hay una larga historia de intentar demostrar la superioridad de un método de votación sobre otro mediante la construcción de ejemplos en los que los dos métodos dan respuestas diferentes, y se afirma triunfalmente que el primer método es correcto y el segundo incorrecto. Dado que se pueden construir ejemplos que son desventajosos para todos los métodos, esta forma de razonamiento puede no ser concluyente. Un ejemplo ocurre arriba donde ilustramos una debilidad en IRV por medio de una elección ficticia en la que el ganador legítimo sería eliminado en la primera vuelta.
Donald Saari ha dado un ejemplo reciente destacado. Volvió a analizar un ejemplo dado por Condorcet de una elección hipotética entre 3 candidatos con 81 votantes cuyas preferencias son las que se muestran en la primera tabla. El ganador de Condorcet es A, que es preferido a B por 41:40 ya C por 60:21; pero el ganador de Borda es B. Condorcet concluyó que el conteo de Borda tuvo la culpa. Saari argumenta que el conteo de Borda es correcto en este caso y señala que los votantes se pueden dividir en 3 grupos, como se muestra en la segunda tabla.
| Número de votantes | Clasificación |
|---|---|
| 10 | A B C |
| 10 | BCA |
| 10 | TAXI |
| 1 | ACB |
| 1 | CBA |
| 1 | BAC |
| 20 | A B C |
| 28 | BAC |
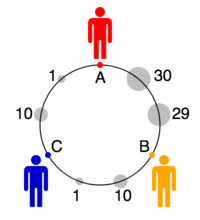
Los grupos rosa y azul consisten en ciclos en sentido horario y antihorario que, según Saari, se cancelan, dejando que el resultado lo determine el grupo blanco; y la clara preferencia de este grupo (nuevamente según Saari) es por B.
El diagrama muestra una posible configuración de los votantes y candidatos consistente con las boletas, con todos ubicados en la circunferencia de un círculo unitario. Confirma el juicio de Saari, en el sentido de que la distancia de A con respecto al votante medio es de 1,15 mientras que la de B es de 1,09 (y la de C es de 1,70), lo que convierte a B en el ganador espacial. Pero es solo un ejemplo. Podemos imaginar manteniendo todas las posiciones fijas excepto la de A, y moviendo A radialmente hacia el centro del círculo. Un paso infinitesimal es suficiente para que A sea la preferencia de los grupos cíclicos, aunque el grupo blanco sigue prefiriendo B. Una vez que la distancia de A desde el centro es inferior a aproximadamente 0,89, la preferencia general cambia de B a A, aunque los votos emitidos serían sin alterar.
Por lo tanto, la elección es ambigua en el sentido de que representaciones espaciales igualmente razonables implican diferentes ganadores. Esta es la ambigüedad que buscamos evitar anteriormente al adoptar una métrica mediana para los modelos espaciales; pero aunque la métrica mediana logra su objetivo en una sola dimensión y se generaliza atractivamente a dimensiones superiores, la propiedad necesaria para evitar la ambigüedad no se generaliza. En general, los ciclos pueden hacer que el ganador espacial sea indeterminado sin referencia a hechos externos. La existencia de una mediana de votantes omnidireccional es condición suficiente para asegurar un resultado determinado de los votos emitidos, y en este caso el ganador espacial es el ganador de Condorcet; y la unidimensionalidad de la distribución de votantes es suficiente para que tenga una mediana omnidireccional.
El ejemplo de Saari ha sido influyente. Darlington recuerda que un "revisor de una revista académica muy prestigiosa" le dijo que un ejemplo similar muestra que el criterio de Condorcet es "ridículo, ya que un conjunto de votos que muestra un empate no debería cambiar el resultado de una elección".
Criterios para las elecciones de un solo ganador
Tradicionalmente, los méritos de los diferentes sistemas electorales se han argumentado con referencia a criterios lógicos. Estos tienen la forma de reglas de inferencia para decisiones electorales, autorizando la deducción, por ejemplo, de que "si E y E ' son elecciones tales que R (E, E '), y si A es el legítimo ganador de E , entonces A es el legítimo ganador de E '".
Los criterios son tan discutibles como los propios sistemas de votación. Aquí discutimos brevemente las consideraciones adelantadas sobre su validez, y luego resumimos los criterios más importantes, mostrando en una tabla cuáles de los principales sistemas de votación los satisfacen.
Epistemología de los criterios de votación
Argumentos del ejemplo

Un ejemplo de mala conducta en un sistema de votación puede generalizarse para dar un criterio que garantice que tal falla no puede surgir de un sistema que satisface el criterio, incluso en casos más complicados. El ejemplo de Saari da el criterio de Cancelación (que es satisfecho por el conteo de Borda pero violado por todos los sistemas Condorcet); el ejemplo ilustrado de IRV eliminando al ganador legítimo puede generalizarse como el criterio de Condorcet (que es violado por el conteo de Borda).
Una generalización más interesante proviene de la clase de ejemplos conocidos como 'paradojas de ausencia' que se pueden ilustrar con el mismo diagrama. Acordando que B es el ganador legítimo, podemos suponer que bajo cierto sistema de votación B será elegido si todos los votantes votan sinceramente, pero que bajo este sistema, un solo partidario de A puede inclinar el resultado hacia su candidato preferido simplemente absteniéndose.. La mayoría de la gente estaría de acuerdo en que este sería un resultado absurdo. Si le diésemos importancia podríamos generalizarlo al criterio de Participación, que dice que un votante nunca puede ayudar más a un candidato absteniéndose que votando.
Es un gran paso del ejemplo al criterio. En el ejemplo, el resultado paradójico es simplemente incorrecto: B sigue siendo el legítimo ganador cuando un partidario de A se abstiene. Pero cuando adoptamos el criterio de Participación, restringimos los resultados electorales en ejemplos complicados en los que es imposible identificar al legítimo ganador, y con consecuencias difíciles de predecir; esto puede ser más de lo que esperábamos.
El criterio de Participación resulta ser sorprendentemente poderoso: rechaza todos los sistemas de Condorcet mientras acepta el conteo de Borda. Pero las paradojas de ausencia que surgen de los sistemas de Condorcet nunca son ejemplos en los que los resultados son simplemente erróneos, sino casos en los que pares de resultados se relacionan de forma indeseable sin ser determinados correctos o erróneos.
Consistencia lógica
Los criterios ampliamente aceptados son mutuamente inconsistentes en varios grupos (el primero de ellos es el grupo de 3 criterios incompatibles identificados por el teorema de imposibilidad de Arrow). También contradicen todos los sistemas de votación. Dan Felsenthal describió 16 criterios y 18 sistemas de votación y mostró "que cada uno de sus 18 sistemas viola al menos seis de esos criterios".
Criterios de resultado (absoluto)
Pasamos ahora a los criterios lógicos en sí mismos, comenzando con los criterios absolutos que establecen que, si el conjunto de votos es de cierta manera, un determinado candidato debe o no debe ganar.Criterio mayoritario (MC)¿Ganará siempre un candidato clasificado como el único favorito por la mayoría de los votantes? Este criterio viene en dos versiones:
- Criterio de mayoría clasificada, en el que una opción que simplemente es preferida por mayoría sobre las demás debe ganar. (Pasar el MC clasificado se indica con " sí " en la tabla a continuación, porque también implica pasar lo siguiente:)
- Criterio de mayoría calificada, en el que solo debe ganar una opción a la que la mayoría otorga una calificación perfecta. Los MC clasificados y calificados son sinónimos de los métodos de votación clasificados, pero no de los calificados o calificados. El MC clasificado, pero no el MC clasificado, es incompatible con el criterio IIA que se explica a continuación.
Criterio de mayoría mutua (MMC)¿Ganará siempre un candidato que esté entre un grupo de candidatos clasificados por encima de todos los demás por la mayoría de los votantes? Esto también implica el criterio del perdedor de la mayoría: si la mayoría de los votantes prefiere a todos los demás candidatos sobre un candidato determinado, ¿entonces ese candidato no gana? Por lo tanto, de los métodos enumerados, todos no pasan ninguno o ambos criterios, excepto Borda, que pasa Perdedor mayoritario y falla Mayoría mutua.criterio de Condorcet¿Siempre ganará un candidato que supere a todos los demás candidatos en las comparaciones por pares? (Esto implica el criterio de la mayoría, arriba).Criterio de perdedor de Condorcet (cond. loser)¿Nunca ganará un candidato que pierda frente a todos los demás candidatos en las comparaciones por pares?
Criterios de resultado (relativo)
Estos son criterios que establecen que, si un determinado candidato gana en una circunstancia, el mismo candidato debe (o no debe) ganar en una circunstancia relacionada.Independencia de las alternativas dominadas por Smith (ISDA)¿El resultado nunca cambia si se agrega o elimina un candidato dominado por Smith (suponiendo que los votos con respecto a los otros candidatos no cambien)? El candidato C está dominado por Smith si hay algún otro candidato A tal que C sea vencido por A y cada candidato B que no sea vencido por A, etc. Tenga en cuenta que aunque este criterio se clasifica aquí como relativo al nominado, tiene un fuerte absoluto componente en la exclusión de los candidatos dominados por Smith de ganar. De hecho, implica todos los criterios absolutos anteriores.Independencia de alternativas irrelevantes (IIA)¿El resultado nunca cambia si se agrega o elimina un candidato no ganador (suponiendo que las preferencias de los votantes con respecto a los otros candidatos no cambien)? Por ejemplo, la regla de pluralidad falla IIA; agregar un candidato X puede hacer que el ganador cambie de W a Y aunque Y no reciba más votos que antes.Independencia local de alternativas irrelevantes (LIIA)¿El resultado nunca cambia si se elimina la alternativa que terminaría en último lugar? (¿Y podría la alternativa que termina en segundo lugar no convertirse en ganadora si se eliminara al ganador?)Independencia de las alternativas de clones (a prueba de clones)¿El resultado nunca cambia si se agregan candidatos no ganadores similares a un candidato existente? Hay tres fenómenos diferentes que podrían causar que un método falle este criterio:spoilersCandidatos que disminuyen la posibilidad de que gane cualquiera de los candidatos similares o clones, también conocido como efecto spoiler.equiposConjuntos de candidatos similares cuya mera presencia aumenta las posibilidades de que cualquiera de ellos gane.multitudesCandidatos adicionales que afectan el resultado de una elección sin ayudar ni perjudicar las posibilidades de su grupo faccional, sino que afectan a otro grupo.Criterio de monotonicidad (monótono)Si el candidato W gana para un juego de boletas, ¿ganará W siempre si esas boletas cambian a una clasificación W más alta? (Esto también implica que no puede hacer que un candidato perdedor gane clasificándolo más abajo).Criterio de consistencia (CC)Si el candidato W gana para un juego de boletas, ¿ganará W siempre si esas boletas cambian agregando otro juego de boletas donde W también gana?Criterio de participación (PC)¿Es siempre mejor votar honestamente que no votar? (Esto se agrupa con el criterio de consistencia distinto pero similar en la tabla a continuación).Simetría inversa (inversión)Si se invierten las preferencias individuales de cada votante, ¿nunca gana el ganador original?
Criterios de conteo de votos
Estos son criterios que se relacionan con el proceso de contar los votos y determinar un ganador.Tiempo polinomial (polytime)¿Se puede calcular el ganador en un tiempo de ejecución que sea polinomial en el número de candidatos y lineal en el número de votantes?Soluble¿Se puede calcular el ganador en casi todos los casos, sin usar ningún proceso aleatorio como lanzar monedas? Es decir, ¿son los empates exactos, en los que el ganador podría ser uno de dos o más candidatos, extremadamente raros en elecciones grandes?Sumabilidad (sumable)¿Se puede calcular el ganador contando los votos en cada colegio electoral por separado y simplemente sumando los recuentos individuales? La cantidad de información necesaria para tales conteos se expresa como una función de orden del número de candidatos N. Las funciones de crecimiento más lento, como O(N) u O(N), facilitan el conteo, mientras que las funciones de crecimiento más rápido, como O(N!) podría dificultar la detección de fraudes por parte de los administradores electorales.
Criterios de estrategia
Estos son criterios que se relacionan con el incentivo de un votante para usar ciertas formas de estrategia. También podrían considerarse como criterios de resultados relativos; sin embargo, a diferencia de los criterios en esa sección, estos criterios son directamente relevantes para los votantes; el hecho de que un método pase estos criterios puede simplificar el proceso de determinar el voto estratégico óptimo.Criterio de ausencia de daño posterior y criterio de ausencia de ayuda posterior¿Pueden los votantes estar seguros de que agregar una preferencia posterior a una boleta no dañará ni ayudará a ningún candidato que ya esté en la lista?Sin traición favorita (NFB)¿Pueden los votantes estar seguros de que no necesitan clasificar a ningún otro candidato por encima de su favorito para obtener el resultado que prefieren?
Formato de boleta
Son cuestiones relativas a la expresividad o contenido informativo de una papeleta válida.tipo de boleta¿Qué información se le da al votante en la boleta?Rangos iguales¿Puede una boleta válida expresar el mismo apoyo a más de un candidato (y no solo la misma oposición a más de uno)?Más de 2 rangos¿Puede una boleta expresar más de dos niveles de apoyo/oposición para diferentes candidatos?
Debilidad
Nota sobre la terminología: Se dice que un criterio es "más débil" que otro cuando se aprueba por más métodos de votación. Con frecuencia, esto significa que las condiciones para que se aplique el criterio son más sólidas. Por ejemplo, el criterio de la mayoría (MC) es más débil que el criterio de la mayoría múltiple (MMC), porque requiere que gane un solo candidato, en lugar de un grupo de cualquier tamaño. Es decir, cualquier método que pase la MMC también pasa la MC, pero no al revés; mientras que cualquier ganador requerido bajo el MC debe ganar bajo el MMC, pero no al revés.
Cumplimiento de métodos seleccionados de ganador único
La siguiente tabla muestra cuáles de los criterios anteriores se cumplen en varios métodos de ganador único.
| Clasificar: | ||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CriterioMétodo | Mayoria | mayorperdedor | mayor mutuo | Condorcet | cond.perdedor | Smith/ISDA | LIIA | IIA | A prueba de clones | Monótono | Consistencia | Participación | simetría inversa | Politiempo/resoluble | Sumable | Más tarde-no- | Sin traiciónfavorita | tipo de boleta | Rangos | |||
| Dañar | Ayudar | = | >2 | |||||||||||||||||||
| Aprobación | Calificado | No | No | No | No | No | Sí | Sí | Sí | Sí | Sí | Sí | Sí | SOBRE) | Sí | SOBRE) | No | Sí | Sí | Aprobaciones | Sí | No |
| cuenta borde | No | Sí | No | No | Sí | No | No | No | equipos | Sí | Sí | Sí | Sí | SOBRE) | Sí | SOBRE) | No | Sí | No | Clasificación | Sí | Sí |
| Bucklin | Sí | Sí | Sí | No | No | No | No | No | No | Sí | No | No | No | SOBRE) | Sí | SOBRE) | No | Sí | Si las mismas preferencias | Clasificación | Sí | Sí |
| Copelandia | Sí | Sí | Sí | Sí | Sí | Sí | No | No | equipos,multitudes | Sí | No | No | Sí | O(N) | No | O(N) | No | No | No | Clasificación | Sí | Sí |
| IRV (AV) | Sí | Sí | Sí | No | Sí | No | No | No | Sí | No | No | No | No | O(N) | Sí | ¡SOBRE!) | Sí | Sí | No | Clasificación | No | Sí |
| Kemeny– Joven | Sí | Sí | Sí | Sí | Sí | Sí | Sí | No | spoilers | Sí | No | No | Sí | ¡SOBRE!) | Sí | O(N) | No | No | No | Clasificación | Sí | Sí |
| Valor medio/mayoritario másalto | Calificado | Sí | No | No | No | No | Sí | Sí | Sí | Sí | No | No | Depende | SOBRE) | Sí | SOBRE) | No | Sí | Sí | Puntuaciones | Sí | Sí |
| minimax | Sí | No | No | Sí | No | No | No | No | spoilers | Sí | No | No | No | O(N) | Sí | O(N) | No | No | No | Clasificación | Sí | Sí |
| Pluralidad/FPTP | Sí | No | No | No | No | No | No | No | spoilers | Sí | Sí | Sí | No | SOBRE) | Sí | SOBRE) | N / A | N / A | No | marca única | N / A | No |
| Puntuación de votación | No | No | No | No | No | No | Sí | Sí | Sí | Sí | Sí | Sí | Sí | SOBRE) | Sí | SOBRE) | No | Sí | Sí | Puntuaciones | Sí | Sí |
| parejas clasificadas | Sí | Sí | Sí | Sí | Sí | Sí | Sí | No | Sí | Sí | No | No | Sí | O(N) | Sí | O(N) | No | No | No | Clasificación | Sí | Sí |
| votación de segunda vuelta | Sí | Sí | No | No | Sí | No | No | No | spoilers | No | No | No | No | SOBRE) | Sí | SOBRE) | Sí | Sí | No | marca única | N / A | No |
| Schulze | Sí | Sí | Sí | Sí | Sí | Sí | No | No | Sí | Sí | No | No | Sí | O(N) | Sí | O(N) | No | No | No | Clasificación | Sí | Sí |
| votación ESTRELLA | No | Sí | No | No | Sí | No | No | No | No | Sí | No | No | Depende | SOBRE) | Sí | O(N) | No | No | No | Puntuaciones | Sí | Sí |
| Sorteo, ganador arbitrario | No | No | No | No | No | No | Sí | Sí | No | Sí | Sí | Sí | Sí | O(1) | No | O(1) | Sí | Sí | Sí | Ninguna | N / A | N / A |
| boleta aleatoria | No | No | No | No | No | No | Sí | Sí | Sí | Sí | Sí | Sí | Sí | SOBRE) | No | SOBRE) | Sí | Sí | Sí | marca única | N / A | No |
Esta tabla no es exhaustiva. Por ejemplo, el método de Coombs no está incluido.
Las comparaciones adicionales de los criterios de votación están disponibles en el artículo sobre el método Schulze (también conocido como ruta de ritmo). Algunos datos pueden estar duplicados ya que estas tablas son un trabajo en progreso.
| Sistema | monótono | Ganador de Condorcet | Mayoria | perdedor de Condorcet | perdedor de la mayoría | mayoría mutua | Herrero | ISDA | LIIA | Independencia de los clones | simetría inversa | Participación, consistencia | Más tarde sin daños | Más tarde sin ayuda | Tiempo polinomial | Resolubilidad |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Schulze | Sí | Sí | Sí | Sí | Sí | Sí | Sí | Sí | No | Sí | Sí | No | No | No | Sí | Sí |
| parejas clasificadas | Sí | Sí | Sí | Sí | Sí | Sí | Sí | Sí | Sí | Sí | Sí | No | No | No | Sí | Sí |
| Alternativa de Tideman | No | Sí | Sí | Sí | Sí | Sí | Sí | Sí | No | Sí | No | No | No | No | Sí | Sí |
| Kemeny-Joven | Sí | Sí | Sí | Sí | Sí | Sí | Sí | Sí | Sí | No | Sí | No | No | No | No | Sí |
| Copelandia | Sí | Sí | Sí | Sí | Sí | Sí | Sí | Sí | No | No | Sí | No | No | No | Sí | No |
| Nanson | No | Sí | Sí | Sí | Sí | Sí | Sí | No | No | No | Sí | No | No | No | Sí | Sí |
| Negro | Sí | Sí | Sí | Sí | Sí | No | No | No | No | No | Sí | No | No | No | Sí | Sí |
| Votación de segunda vuelta instantánea | No | No | Sí | Sí | Sí | Sí | No | No | No | Sí | No | No | Sí | Sí | Sí | Sí |
| Smith/IRV | No | Sí | Sí | Sí | Sí | Sí | Sí | Sí | No | Sí | No | No | No | No | Sí | Sí |
| Borda | Sí | No | No | Sí | Sí | No | No | No | No | No | Sí | Sí | No | Sí | Sí | Sí |
| balduino | No | Sí | Sí | Sí | Sí | Sí | Sí | No | No | No | No | No | No | No | Sí | Sí |
| Bucklin | Sí | No | Sí | No | Sí | Sí | No | No | No | No | No | No | No | Sí | Sí | Sí |
| Pluralidad | Sí | No | Sí | No | No | No | No | No | No | No | No | Sí | Sí | Sí | Sí | Sí |
| voto contingente | No | No | Sí | Sí | Sí | No | No | No | No | No | No | No | Sí | Sí | Sí | Sí |
| coombs | No | No | Sí | Sí | Sí | Sí | No | No | No | No | No | No | No | No | Sí | Sí |
| minimax | Sí | Sí | Sí | No | No | No | No | No | No | No | No | No | No | No | Sí | Sí |
| Anti-pluralidad | Sí | No | No | No | Sí | No | No | No | No | No | No | Sí | No | No | Sí | Sí |
| Voto contingente de Sri Lanka | No | No | Sí | No | No | No | No | No | No | No | No | No | Sí | Sí | Sí | Sí |
| voto suplementario | No | No | Sí | No | No | No | No | No | No | No | No | No | Sí | Sí | Sí | Sí |
| dodgson | No | Sí | Sí | No | No | No | No | No | No | No | No | No | No | No | No | Sí |
Comparación de sistemas multiganador
Los sistemas electorales de múltiples ganadores buscan producir asambleas representativas en un sentido más amplio que el de tomar las mismas decisiones que se tomarían con los votos de un solo ganador. La Comisión Real de Nueva Zelanda sobre el Sistema Electoral enumeró diez criterios para su evaluación de posibles nuevos métodos electorales para Nueva Zelanda. Estos incluían la equidad entre los partidos políticos, la representación efectiva de grupos minoritarios o de intereses especiales, la integración política, la participación efectiva de los votantes y la legitimidad.
Métricas para evaluaciones de múltiples ganadores
La evaluación del rendimiento de los métodos de votación de múltiples ganadores requiere métricas diferentes a las que se utilizan para los sistemas de un solo ganador. Se han propuesto las siguientes.
- La Eficiencia del Comité Condorcet (CCE) mide la probabilidad de que un grupo de ganadores electos supere a todos los perdedores en carreras por parejas.
- La proporcionalidad de utilidad social (SUP) mide la probabilidad de que cada votante tenga al menos un candidato de alta utilidad entre los ganadores.
- La proporcionalidad de utilidad igualitaria (EUP) mide la proporcionalidad en términos del votante con la utilidad más baja para el candidato ganador más cercano.
- La Tendencia Centrista (CT) mide la probabilidad de que un método elija candidatos cerca del centro o extremos de un espectro político.
Tablas de criterios
Cumplimiento de los métodos de múltiples ganadores basados en partidos
| CriterioMétodo | Proporcional en teoría | Proporcional en la práctica | Semi-proporcionaluna mayoría de votantes no puede forzar el resultado para que ganen todos los escaños | El método de votación no rompible no tiene un ciclo de retroalimentación de votación estratégica potencial | Monótono | Consistencia | Participación | Candidatos universalmente queridos | ¿Hay niveles de miembros? | ¿Se requiere representación local? | ¿Hay selección de votantes de candidatos individuales? | Tipo de boleta |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Entrada general | No | No | No | No – Dominación bipartidista | Sí | Sí | Sí | No | No | No | No, todos los asientos se llenan de una lista predeterminada | Marca única para una lista |
| Lista de fiestas cerrada | Sí | Sí | Sí | Sí (a menos que haya pocos asientos o un umbral alto para el primer asiento) | Sí | Sí | Sí | N/A: por definición, una lista universal tendría que ganar todos los escaños | No | No | No, la clasificación de los candidatos dentro de la lista del partido determina el orden en que se llenan los escaños del partido. | Marca única para una lista |
| Lista de partidos relativamente cerrada | Sí | Sí | Sí | Sí (a menos que haya pocos asientos o un umbral alto para el primer asiento) | Sí | Sí | Sí | N/A: por definición, una lista universal tendría que ganar todos los escaños | No | No | Sí, un candidato debe obtener una cuota Hare para garantizar un escaño; de lo contrario, la clasificación de los candidatos dentro de la lista del partido determina el orden en que se llenan los escaños del partido. | Marcas únicas o limitadas para candidatos dentro de una lista |
| Lista de partidos más abierta | Sí | Sí | Sí | Sí (a menos que haya pocos asientos o un umbral alto para el primer asiento) | Sí | Sí | Sí | N/A: por definición, una lista universal tendría que ganar todos los escaños | No | No | Sí, un candidato debe obtener una proporción de los votos para garantizar un escaño; de lo contrario, la clasificación de los candidatos dentro de la lista del partido determina el orden en que se llenan los escaños del partido. | Marcas únicas o limitadas para candidatos dentro de una lista |
| Lista de partidos más abierta | Sí | Sí | Sí | Sí (a menos que haya pocos asientos o un umbral alto para el primer asiento) | Sí | Sí | Sí | N/A: por definición, una lista universal tendría que ganar todos los escaños | No | No | Sí, la cantidad de votos que recibe cada candidato determina el orden en que se llenan los escaños del partido. | Marca única para un candidato dentro de una lista |
| Lista de fiestas con estilo | Sí | Sí | Sí | Sí (a menos que haya pocos asientos o un umbral alto para el primer asiento) | Sí | Sí | Sí | N/A: por definición, una lista universal tendría que ganar todos los escaños | No | No | Sí, la cantidad de votos que recibe cada candidato determina el orden en que se llenan los escaños del partido. | Marcas limitadas para los candidatos dentro de todas las listas |
| Proporcional de miembros mixtos sin modificar | No: los votantes estratégicos pueden manipular la cantidad de escaños sobresalientes | Sí, excluyendo las desproporcionalidades causadas por los escaños superpuestos: los miembros del nivel proporcional se seleccionan para compensar cualquier desproporcionalidad causada por el nivel del distrito electoral, según los votos del nivel proporcional únicamente | Sí | No: manipulación de voladizo y dominación bipartidista entre escaños de un solo ganador | Sí | No | Sí | Parcialmente: una lista del agrado universal tendría que ganar todos los escaños en los niveles proporcional y de distrito por definición; si todos los candidatos de la circunscripción son del agrado universal, la selección de miembros de nivel proporcional se haría para compensar la desproporcionalidad resultante en la membresía general | Sí: nivel de circunscripción y nivel proporcional | Sí, distritos uninominales | Sí: los candidatos de las circunscripciones se seleccionan mediante un método de ganador único; la selección de miembros de nivel proporcional se puede hacer mediante cualquiera de los métodos de lista de partidos mencionados anteriormente | Marca única o clasificación para un candidato de circunscripción; las marcas de nivel proporcionales dependen del método exacto utilizado para la selección |
| Mejor perdedor proporcional de miembros mixtos | No: los votantes estratégicos pueden manipular la cantidad de escaños sobresalientes | Sí, excluyendo las desproporcionalidades causadas por escaños superpuestos: los miembros del nivel proporcional se seleccionan para compensar cualquier desproporcionalidad causada por el nivel de circunscripción, en función de los totales del partido. | Sí | No: manipulación de voladizo y dominación bipartidista entre escaños de un solo ganador | Sí | No | Sí | No, por definición, una lista del agrado universal tendría que ganar todos los escaños tanto en el nivel proporcional como en el de distrito electoral, dado que los miembros del nivel proporcional provienen de los perdedores del distrito electoral, tal hazaña es imposible; si todos los candidatos de la circunscripción son del agrado universal, la selección de miembros de nivel proporcional se haría para compensar la desproporcionalidad resultante en la membresía general | Sí: nivel de circunscripción y nivel proporcional | Sí, distritos uninominales | Sí: los candidatos de las circunscripciones se seleccionan mediante un método de ganador único; los miembros del nivel proporcional se seleccionan mediante un método de lista de partidos | Marca única o clasificación para un candidato de circunscripción; nivel proporcional determinado por los resultados del nivel del distrito electoral |
| votación paralela | No | No: los miembros del nivel de circunscripción y del nivel proporcional se seleccionan de forma independiente entre sí | Sí | No: dominación bipartidista entre los escaños de un solo ganador | Sí | No | Sí | Parcialmente: una lista universalmente aceptada tendría que ganar todos los escaños en el nivel proporcional por definición; si todos los candidatos del distrito electoral gustan universalmente, la selección de miembros de nivel proporcional no se vería afectada | Sí: nivel de circunscripción y nivel proporcional | Sí, distritos uninominales | Sí: los candidatos de las circunscripciones se seleccionan mediante un método de ganador único; los miembros del nivel proporcional se seleccionan mediante un método de lista de partidos | Marca única o clasificación para un candidato de circunscripción; las marcas de nivel proporcionales dependen del método exacto utilizado para la selección |
| Escorpio | No: los votantes estratégicos pueden dividir la boleta para desquiciar la resta compensatoria, revirtiendo así la elección a votación paralela | Parcialmente: los miembros del nivel de circunscripción y del nivel proporcional se seleccionan de forma independiente, pero los votos de los ganadores de la circunscripción se restan de los totales de las listas de sus respectivos partidos. | Sí | No – listas de señuelos | No | No | No | Sí, a una lista que gusta universalmente todavía se le restan los votos de los ganadores de su circunscripción de su propio total, lo que garantiza una distribución proporcional entre todos los demás escaños; si todos los candidatos de la circunscripción son del agrado universal, la selección de los miembros del nivel proporcional se haría con sus votos restados de los totales de sus partidos | Sí: nivel de circunscripción y nivel proporcional | Sí, distritos uninominales | Sí: los candidatos de las circunscripciones se seleccionan mediante un método de ganador único; los miembros del nivel proporcional se seleccionan mediante un método de lista de partidos | Marca única o clasificación para un candidato de circunscripción; las marcas de nivel proporcionales dependen del método exacto utilizado para la selección |
| Sistema de bonificación mayoritaria | Parcialmente: la mayoría de los escaños se distribuyen proporcionalmente entre los partidos, pero el resto se otorga como bonificación al partido más votado; Los votantes estratégicos pueden manipular este bono | Parcialmente: la mayoría de los escaños se distribuyen proporcionalmente entre los partidos, pero el resto se otorga como bonificación al partido más votado. | Sí | No: dominación bipartidista entre las partes que compiten por la bonificación | Sí | Sí | Sí | N/A: por definición, una lista universal tendría que ganar todos los escaños | Sí, nivel proporcional y nivel de bonificación | No | No necesariamente: la selección de miembros de nivel proporcional se puede realizar mediante cualquiera de los métodos de listas de partidos mencionados anteriormente. | Las marcas de nivel proporcionales dependen del método exacto utilizado para la selección; nivel de bonificación determinado por los resultados del nivel proporcional |
| Sistema de bote mayoritario | No: el premio mayor se asigna al partido más votado y los asientos del nivel sin premio mayor se distribuyen proporcionalmente entre todos los demás; Los votantes estratégicos pueden manipular el premio mayor | No: el premio mayor se asigna al partido más votado y los asientos del nivel sin premio mayor se distribuyen proporcionalmente entre todos los demás | Sí | No: dominación bipartidista entre las partes que compiten por el premio mayor | No, la parte que gana el premio mayor obtiene una ventaja sobre todos los demás; el premio mayor se convierte en una desventaja para el partido más votado si obtuvo una mayor proporción de escaños que el premio mayor | Sí | Sí | N/A: por definición, una lista universal tendría que ganar todos los escaños | Sí, nivel proporcional y nivel de premio mayor | No | No necesariamente: la selección de miembros de nivel proporcional se puede realizar mediante cualquiera de los métodos de listas de partidos mencionados anteriormente. | Las marcas de nivel proporcionales dependen del método exacto utilizado para la selección; nivel de premio mayor determinado por los resultados del nivel proporcional |
| Proporcional de dos miembros | No: los votantes estratégicos teóricamente pueden manipular los resultados en escaños secundarios | Sí | Sí | No: manipulación de escaños secundarios y dominación bipartidista entre escaños primarios | No | Sí | Sí | Sí | No | Sí, distritos electorales de dos miembros | Sí, el candidato con más votos tiene garantizado un escaño y el otro se selecciona entre los mejores perdedores. | Marca única para un candidato o par de candidatos |
| Representación proporcional rural-urbana | No: los votantes estratégicos pueden manipular la cantidad de escaños rurales sobresalientes | Parcialmente: las desproporcionalidades pueden ser causadas por el uso de STV en asientos urbanos, así como en asientos rurales sobresalientes: los miembros del nivel proporcional rural se seleccionan para compensar cualquier desproporcionalidad causada por el nivel de distrito electoral rural, pero no existe tal compensación para las desproporcionalidades urbanas | Sí | No: manipulación de voladizo y dominación bipartidista entre los escaños rurales ganadores individuales | No | No | No | Parcialmente, sí en el nivel urbano; una lista rural del agrado universal tendría que ganar todos los escaños en el nivel rural proporcional por definición; si todos los candidatos de las circunscripciones rurales son aceptados universalmente, la selección de los miembros rurales proporcionales se haría para compensar la desproporcionalidad; en cualquier caso, la selección de candidatos urbanos no se vería afectada | Sí: nivel urbano, nivel de circunscripción rural y nivel proporcional rural | Sí: distritos electorales urbanos y distritos electorales rurales uninominales | Sí, los candidatos de las circunscripciones rurales son seleccionados por STV; los candidatos de las circunscripciones rurales se seleccionan mediante un método de ganador único; Los miembros rurales del nivel proporcional pueden ser seleccionados por un método de lista partidaria o entre los mejores perdedores en los distritos electorales rurales. | Ranking de candidatos de circunscripciones urbanas; puntuación única o clasificación para un candidato de circunscripción rural; las marcas de nivel proporcionales rurales dependen del método exacto utilizado para la selección |
Cumplimiento de métodos de múltiples ganadores no mayoritarios agnósticos del partido
La siguiente tabla muestra cuáles de los criterios anteriores se cumplen en varios métodos ganadores múltiples.
| CriterioMétodo | Proporcional | Monótono | Consistencia | Criterio de participación de varios ganadores de Warren | Sin traiciónfavorita | semihonesto | Candidatos universalmente queridos | Con ganador único | Tipo de boleta |
|---|---|---|---|---|---|---|---|---|---|
| Monroe (versión de votación de partitura) | Sí | Depende del desempate utilizado | Sí | No | No | Aprobación o Rango | Aprobaciones o puntajes | ||
| Regla de Chamberlin-Courant | |||||||||
| de Ebert | Sí | No | Sí | Aprobación o Rango | Aprobaciones o puntajes | ||||
| Psi | Sí | Sí | Sí | No | No | No | Aprobación o Rango | Aprobaciones o puntajes | |
| Armónico | Sí | Sí | Sí | No | No | No | Aprobación o Rango | Aprobaciones o puntajes | |
| Aprobación proporcional secuencial | Sí | Sí | No | No | No | No | Aprobación | Aprobaciones | |
| Rango Re-ponderado | Sí | Sí | No | No | No | No | Distancia | Puntuaciones | |
| Aprobación proporcional | Sí | Sí | Sí | No | No | No | Aprobación | Aprobaciones | |
| Votación de ofertas | Sí | No | No | Sí | Aprobación o Rango | Aprobaciones o puntajes | |||
| Voto único transferible | Sí | No | No | No | No | No | Sí | Escorrentía instantánea | clasificaciones |
| CPO-STV | Sí | No | No | No | No | No | Sí | Un método Condorcet (depende de cuál) | clasificaciones |
| Schulze STV | Sí | Sí | No | No | No | No | Sí | Schulze | clasificaciones |
| Expansión de la regla de aprobaciones | Aprobación | Aprobaciones | |||||||
| Voto único intransferible | No | Sí | Sí | Sí | No | No | N/A (no proporcional) | Pluralidad | marca única |
| Voto limitado | No | Sí | Sí | Sí | No | No | N/A (no proporcional) | Pluralidad | marcas limitadas |
| Votación acumulativa | No | Sí | Sí | Sí | No | No | N/A (no proporcional) | Pluralidad | Múltiples marcas |
| Aprobación Minmax | Aprobación | Aprobaciones | |||||||
| Sorteo, ganador arbitrario | No | Sí | Sí | Sí | Sí | Sí | N/A (no proporcional) | Sorteo, ganador arbitrario | Ninguna |
| Boleta aleatoria única | No | Sí | Sí | Sí | Sí | Sí | N/A (no proporcional) | Boleta aleatoria | marcas limitadas |
| Múltiples boletas aleatorias | Enfoques | Sí | Sí | Sí | Sí | Sí | N/A (no proporcional) | Boleta aleatoria | clasificaciones limitadas |
Cumplimiento de métodos de múltiples ganadores agnósticos de partidos mayoritarios
La siguiente tabla muestra cuáles de los criterios anteriores se cumplen en varios métodos ganadores múltiples.
| CriterioMétodo | Monótono | Consistencia | Participación | A prueba de clones | Sin traición favorita | semihonesto | Ganadores del set de Smith | Ganador de Condorcet | perdedor de Condorcet | Con un solo ganador | tipo de boleta |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Aprobación de ganadores múltiples | Sí | Sí | Sí | Sí | Sí | Sí | No | No | No | Aprobación | Aprobaciones |
| Rango de múltiples ganadores | Sí | Sí | Sí | Sí | Sí | Sí | No | No | No | Distancia | Puntuaciones |
| Schulze ganador múltiple | Sí | No | No | Sí | No | No | Sí | Sí | Sí | Schulze | clasificaciones |
| En general | Sí | Sí | Sí | No(spoilers) | No | No | No | No | No | Pluralidad | marcas limitadas |
Contenido relacionado
Sufragio
Miembro del congreso
Elección intermedia