Coma pitagórica

Pythagorean comma (531441:524288) on C Jugar(help·info).

Pythagorean coma en C usando la notación de Ben Johnston. La nota representada como inferior en el personal (Bongo++++) es ligeramente superior en el campo (que C)♮).

Pythagorean commaPC) definido en el afinado pitagórico como diferencia entre semitonas (A1 – m2), o intervalo entre notas enharmonically equivalente (desde D. a C▪). El segundo disminuido tiene el mismo ancho pero una dirección opuesta (de a C▪ D.).

En afinación musical, el Pythagorean comaa (o ditonic comma), nombrado por el antiguo matemático y filósofo Pythagoras, es el pequeño intervalo (o coma) existente en el afinamiento pitagórico entre dos notas enharmonicamente equivalentes como C y B▪ ()Jugar(help·info)), o D. y C▪. Es igual a la relación frecuencial (1.5)¹².2⁷ = 531441.524288 ≈ 1.01364, o alrededor de 23.46 centavos, aproximadamente una cuarta parte de un semitone (en entre 75:74 y 74:73). La coma que los temperamentos musicales a menudo "temper" es la coma pitagórica.

La coma pitagórica también se puede definir como la diferencia entre un apótomo pitagórico y una limma pitagórica (es decir, entre un semitono cromático y un semitono diatónico, según se determina en la afinación pitagórica); la diferencia entre 12 quintas perfectas y siete octavas; o la diferencia entre tres dítonos pitagóricos y una octava (es por eso que la coma pitagórica también se llama coma dítónica).

La segunda disminuida, en afinación pitagórica, se define como la diferencia entre limma y apotome. Coincide, por tanto, con lo contrario de una coma pitagórica, y puede verse como una coma pitagórica descendente (por ejemplo, de C♯ a D♭), equivalente a unos −23,46 centavos.

Derivación

Como se describe en la introducción, la coma pitagórica se puede derivar de varias maneras:

• Difference between two enharmonically equivalent notes in a Pythagorean scale, such as C and B▪ ()Jugar(help·info)), o D. y C▪ (véase infra).
• Difference between Pythagorean apotome and Pythagorean limma.
• Diferencia entre 12 quintas y siete octavas perfectas.
• Difference between three Pythagorean ditones (major tercios) and one octave.

Una quinta perfecta tiene una relación de frecuencia de 3:2. Se utiliza en la afinación pitagórica, junto con la octava, como vara de medir para definir, con respecto a una nota inicial dada, la frecuencia de cualquier otra nota.

Apotome y limma son los dos tipos de semitonos definidos en la afinación pitagórica. Es decir, el apótomo (alrededor de 113,69 centavos, por ejemplo, de C a C ♯) es el semitono cromático, o unísono aumentado (A1), mientras que la limma (alrededor de 90,23 centésimas, por ejemplo, de C a D♭) es el semitono diatónico o segundo menor (m2).

Un ditono (o tercera mayor) es un intervalo formado por dos tonos mayores. En la afinación pitagórica, un tono mayor tiene un tamaño de aproximadamente 203,9 centavos (relación de frecuencia 9:8), por lo que un dítono pitagórico tiene aproximadamente 407,8 centavos.

Octaves (7 × 1200 = 8400) versus quintos (12 × 701.96 = 8423.52), representado como con varas Cuisenaire (red (2) se utiliza para 1200, negro (7) se utiliza para 701.96).

Octaves (1 × 1200 = 1200) versus ditones (3 × 407.82 = 1223.46), representado como con varas Cuisenaire (red (2) se utiliza para 1200, magenta (4) se utiliza para 407.82).

Tamaño

El tamaño de una coma pitagórica, medida en centavos, es

apotome− − limma.. 113.69− − 90.23.. 23.46centavos{displaystyle {hbox{apotome}-{hbox{limma}approx 113.69-90.23approx 23.46~{hbox{cents}!}

o más exactamente, en términos de relaciones de frecuencia:

apotomelimma=37/21128/35=312219=531441524288=1.0136432647705078125{fnMicroc {fnhbox{apotome} {hbox{limma}}={frac} {3^{7}/2^{11}{2^{8}}={5}={frac {3^{12}}{2^{19}}}}=frac {531441}{524288}=1.01364326477058125}}}}} {0}} {3}}}} {3}}} {3}} {3}}}}} {3} {3}}}}}}=0}=0}=0}=0}=0}=0}=0=0}=0=0=0=0=0=0=0=0=0=0=0=0=0=0=0=0=0=0=0=0=0=0=0=0=0=0=0=0=0=0=0=0=0=0=0=0=0=0=0=0=0=0=0

La coma Pythagorean mostró como la brecha (en el lado derecho) que hace que una estrella de 12 puntos no se cierre, que estrella representa la escala pitagórica; cada línea representa una quinta perfecta. Esa brecha tiene un ángulo central de 7.038 grados, que es 23.46% de 30 grados.

Círculo de quintas y cambio enarmónico

Pythagorean coma como doce quintas perfectas en la notación de Ben Johnston.

La coma Pythagorean también se puede considerar como la discrepancia entre 12 quintas perfectas apenas sintonizadas (ratio 3:2) (Jugar(help·info)) y siete octavas (ratio 2:1):

doce quintas partessiete octavas=()32)12/27=312219=531441524288=1.0136432647705078125{displaystyle {frac {hbox{twelve fifths}}{hbox{seven octaves}}=left({tfrac {3}{2}}right)^{12}!{!! {cH00} {cH00}} {cH00}}}}}}}cH00} {cH00}}}}}}}}}cH00}cccH00}ccH00}cH00}cH00}cH00}ccH00}cH00}ccH00}ccH00}ccccH00}cH00}ccH00}cccH00}cH00}ccH00}cH00}cH00}cH00}cH00}ccH00}ccH00}ccH00} Big /},2^{7}={frac {3^{12}{2^{19}={frac {531441}{524288}=1.0136477058125!}

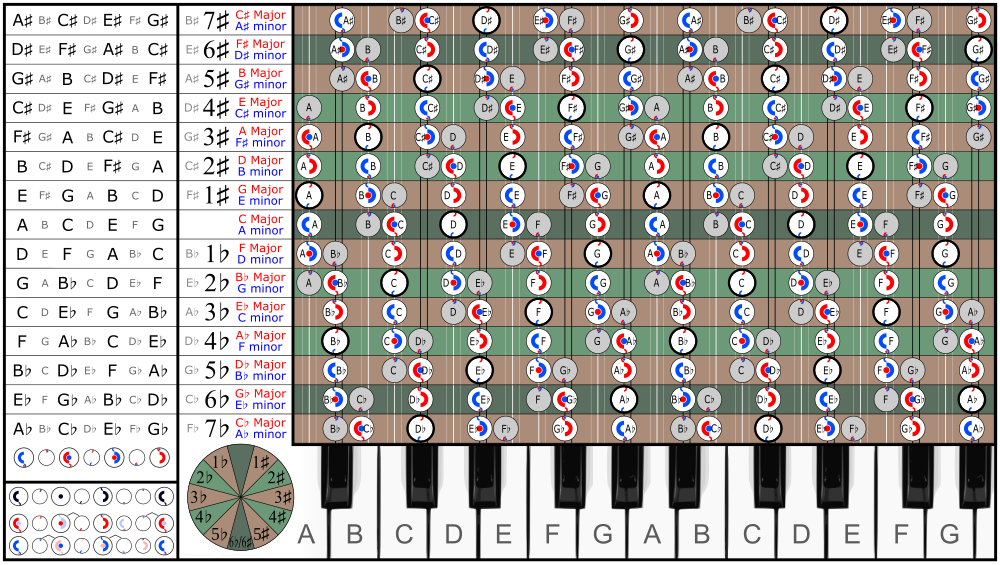
En la siguiente tabla de escalas musicales en el círculo de quintas, la coma pitagórica es visible como el pequeño intervalo entre, por ejemplo, F♯ y G♭. Dar la vuelta al círculo de quintas con solo intervalos da como resultado una bomba de coma por la coma pitagórica.

Los 6♭ y las 6♯ escalas* no son idénticos, aunque están en el teclado del piano, pero ♭ las escalas son una coma pitagórica más abajo. Ignorar esta diferencia conduce a un cambio enarmónico.

* Los 7♭ y 5♯, respectivamente 5♭ y 7♯ las escalas difieren en el de la misma manera por una coma pitagórica. Las escalas con siete alteraciones rara vez se utilizan porque las escalas enarmónicas con cinco alteraciones se tratan como equivalentes.

Este intervalo tiene serias implicaciones para los diversos esquemas de afinación de la escala cromática, porque en la música occidental, 12 quintas perfectas y siete octavas se tratan como el mismo intervalo. El temperamento igual, hoy en día el sistema de afinación más común en Occidente, reconcilió esto al aplanar cada quinto por un doceavo de una coma pitagórica (aproximadamente 2 centavos), produciendo así octavas perfectas.

Otra forma de expresar esto es que el quinto justo tiene una relación de frecuencia (en comparación con la tónica) de 3:2 o 1,5 a 1, mientras que el séptimo semitono (basado en 12 divisiones logarítmicas iguales de una octava) es el séptimo potencia de la raíz doceava de dos o 1,4983... a 1, que no es exactamente lo mismo (una diferencia de aproximadamente 0,1%). Lleva la quinta a la 12ª potencia, luego resta siete octavas y obtienes la coma pitagórica (alrededor de una diferencia de 1,4%).

Historia

El primero en mencionar la proporción de coma de 531441:524288 fue Euclides, quien toma como base el tono entero de la afinación pitagórica con la proporción de 9:8, la octava con la proporción de 2:1, y un número A = 262144. Concluye que elevando este número seis tonos enteros se obtiene un valor, G, que es mayor que el que se obtiene al elevarlo una octava (dos veces A). Él da a G para ser 531441. Los cálculos necesarios dicen:

Cálculo de G:

262144⋅ ⋅ ()98)6=531441{displaystyle 262144cdot left(textstyle {frac {9}{6}=531441}

Cálculo del doble de A:

262144⋅ ⋅ ()21)1=524288{displaystyle 262144cdot left(textstyle {frac {2}{1}derecha)}=524288}

Los matemáticos chinos conocían la coma pitagórica desde el año 122 a. C. (su cálculo se detalla en el Huainanzi), y alrededor del año 50 a. C., Ching Fang descubrió que si se continuaba con el ciclo de quintas perfectas más allá de 12 hasta llegar a 53, la diferencia entre este tono 53 y el tono inicial sería mucho menor que la coma pitagórica. Este intervalo mucho más pequeño se denominó más tarde como la coma de Mercator (ver: historia de 53 temperamentos iguales).

En Lydian Chromatic Concept of Tonal Organisation (1953) de George Russell, el medio paso entre Lydian Tonic y ♭2 en sus escalas Altered Major y Minor Auxiliary Disminished Blues se basa teóricamente en la coma pitagórica.