Cola de prioridad
En informática, una cola de prioridad es un tipo de datos abstracto similar a una cola normal o estructura de datos de pila. Cada elemento en una cola de prioridad tiene una prioridad asociada. En una cola de prioridad, los elementos con alta prioridad se sirven antes que los elementos con baja prioridad. En algunas implementaciones, si dos elementos tienen la misma prioridad, se sirven en el mismo orden en que se pusieron en cola. En otras implementaciones, el orden de los elementos con la misma prioridad no está definido.
Si bien las colas de prioridad a menudo se implementan mediante montones, conceptualmente son distintas de los montones. Una cola de prioridad es una estructura de datos abstracta como una lista o un mapa; Así como una lista se puede implementar con una lista enlazada o con una matriz, una cola de prioridad se puede implementar con un montón u otro método, como una matriz desordenada.
Operaciones
Una cola de prioridad debe admitir al menos las siguientes operaciones:
- is_empty: comprobar si la cola no tiene elementos.
- insert_with_prioridad: añadir un elemento a la cola con una prioridad asociada.
- pull_highest_priority_element: eliminar el elemento de la cola que tiene el máxima prioridad, y devolverlo.
- Esto también se conoce como "pop_element(Off)", "get_maximum_element"o"get_front(mos)_element".
- Algunas convenciones revierten el orden de prioridades, considerando que los valores inferiores son más prioritarios, por lo que esto también puede ser conocido como "get_minimum_element", y a menudo se conoce como "get-min"en la literatura.
- Esto puede ser especificado como separado "peek_at_highest_priority_element"y"delete_element" funciones, que se pueden combinar para producir "pull_highest_priority_element".
Además, peek (en este contexto a menudo llamado find-max o find-min), que devuelve el elemento de mayor prioridad pero no modifica la cola, se implementa con mucha frecuencia y casi siempre se ejecuta en tiempo O(1). Esta operación y su rendimiento O(1) es crucial para muchas aplicaciones de colas de prioridad.
Las implementaciones más avanzadas pueden admitir operaciones más complicadas, como pull_lowest_priority_element, inspeccionar los primeros elementos de mayor o menor prioridad, borrar la cola, borrar subconjuntos de la cola, realizar una inserción por lotes, fusionar dos o más colas en una, incrementar la prioridad de cualquier elemento, etc.
Las pilas y las colas se pueden implementar como tipos particulares de colas de prioridad, con la prioridad determinada por el orden en que se insertan los elementos. En una pila, la prioridad de cada elemento insertado aumenta monótonamente; por lo tanto, el último elemento insertado es siempre el primero que se recupera. En una cola, la prioridad de cada elemento insertado disminuye monótonamente; por lo tanto, el primer elemento insertado es siempre el primero que se recupera.
Implementación
Implementaciones ingenuas
Existe una variedad de formas simples, generalmente ineficientes, de implementar una cola de prioridad. Proporcionan una analogía para ayudar a comprender qué es una cola de prioridad.
Por ejemplo, uno puede mantener todos los elementos en una lista desordenada (O(1) tiempo de inserción). Siempre que se solicite el elemento de mayor prioridad, busque entre todos los elementos el que tenga la mayor prioridad. (O(n) tiempo de extracción),
insertar(nodo)
{}
list.append(node)
}
Tira()
{}
más alta = list.get_first_element()
por cada nodo en la lista
{}
si es más alto. prioridad
{}
máximo = nodo
}
}
list.remove(highest)
más alto
}
En otro caso, se pueden mantener todos los elementos en una lista ordenada por prioridad (O(n) tiempo de ordenación por inserción), siempre que se solicite el elemento de mayor prioridad, el primero de la lista se puede devolver (O(1) tiempo de extracción)
insertar(nodo)
{}
de la lista
{}
si nodo. prioridad
{}
list.insert_at_index(node,index)
descanso
}
}
}
Tira()
{}
más alto = list.get_at_index(list.length-1)
list.remove(highest)
más alto
}
Implementación habitual
Para mejorar el rendimiento, las colas de prioridad generalmente se basan en un montón, dando un rendimiento O(log n) para inserciones y eliminaciones, y O(n) para construir el montón inicialmente a partir de un conjunto de n elementos. Las variantes de la estructura básica de datos del montón, como el emparejamiento de montones o los montones de Fibonacci, pueden proporcionar mejores límites para algunas operaciones.
Alternativamente, cuando se usa un árbol de búsqueda binario autoequilibrado, la inserción y la eliminación también toman tiempo O(log n), aunque se construyen árboles a partir de secuencias de elementos existentes. toma tiempo O(n log n); esto es típico donde uno ya puede tener acceso a estas estructuras de datos, como con bibliotecas estándar o de terceros. Desde el punto de vista de la complejidad del espacio, el uso de un árbol de búsqueda binario autoequilibrado con una lista vinculada requiere más almacenamiento, ya que requiere almacenar referencias adicionales a otros nodos.
Desde el punto de vista de la complejidad computacional, las colas de prioridad son congruentes con los algoritmos de clasificación. La sección sobre la equivalencia de las colas de prioridad y los algoritmos de clasificación, a continuación, describe cómo los algoritmos de clasificación eficientes pueden crear colas de prioridad eficientes.
Montones especializados
Hay varias estructuras de datos de montón especializadas que proporcionan operaciones adicionales o superan las implementaciones basadas en montón para tipos específicos de claves, específicamente claves enteras. Supongamos que el conjunto de claves posibles es {1, 2,..., C}.
- Cuando sólo insertar, find-min y extracto-min son necesarios y en caso de prioridades enteros, una cola de cubo se puede construir como una variedad de C listas vinculadas más un puntero arriba, inicialmente C. Insertar un artículo con clave k apéndices del tema k'th, y actualizaciones top ← min(top, k), ambos en tiempo constante. Extracto-min borra y devuelve un elemento de la lista con índice arriba, luego aumentos arriba si es necesario hasta que de nuevo apunta a una lista no vacía; esto toma O()C) tiempo en el peor caso. Estas colas son útiles para clasificar los vértices de un gráfico por su grado.
- Un árbol de van Emde Boas soporta mínimo, máximo, insertar, Borrador, búsqueda, extracto-min, extracto-max, predecesor y sucesor] operaciones en O(log log C) tiempo, pero tiene un costo espacio para pequeñas colas de alrededor O(22)m/2), donde m es el número de bits en el valor prioritario. El espacio se puede reducir significativamente con la piratería.
- El árbol de Fusión de Fredman y Willard implementa el mínimo en funcionamiento O1) tiempo y insertar y extracto-min operaciones en O()log n/log log C){displaystyle O(log n/log log C)}tiempo. Sin embargo, el autor afirma que "Nuestros algoritmos sólo tienen interés teórico; los factores constantes implicados en los tiempos de ejecución excluyen la practicidad".
Para aplicaciones que hacen muchas "vistas" operaciones por cada "extract-min" operación, la complejidad del tiempo para las acciones de inspección se puede reducir a O(1) en todas las implementaciones de árbol y montón almacenando en caché el elemento de mayor prioridad después de cada inserción y eliminación. Para la inserción, esto agrega como máximo un costo constante, ya que el elemento recién insertado se compara solo con el elemento mínimo previamente almacenado en caché. Para la eliminación, esto como máximo agrega un "vistazo" adicional. costo, que suele ser más barato que el costo de eliminación, por lo que la complejidad del tiempo general no se ve afectada significativamente.
Las colas de prioridad monótonas son colas especializadas que están optimizadas para el caso en que nunca se inserte ningún elemento que tenga una prioridad más baja (en el caso de un montón mínimo) que cualquier elemento extraído previamente. Esta restricción se cumple con varias aplicaciones prácticas de las colas de prioridad.
Resumen de los tiempos de ejecución
Estas son las complejidades de tiempo de varias estructuras de datos de almacenamiento dinámico. Los nombres de las funciones asumen un montón mínimo. Para el significado de "O(f)" y "Θ(f)" ver notación Big O.
| Operación | find-min | eliminar-min | insertar | disminucion-key | sold |
|---|---|---|---|---|---|
| binario | .1) | .(logn) | O(logn) | O(logn) | .()n) |
| Izquierda | .1) | .(log n) | .(log n) | O(log n) | .(log n) |
| Binomial | .1) | .(log n) | .1) | .(log n) | O(logn) |
| Fibonacci | .1) | O(logn) | .1) | .1) | .1) |
| Pareja | .1) | O(log n) | .1) | o(logn) | .1) |
| Brodal | .1) | O(logn) | .1) | .1) | .1) |
| Rank-pairing | .1) | O(log n) | .1) | .1) | .1) |
| Fibonacci estricta | .1) | O(log n) | .1) | .1) | .1) |
| 2-3 montones | O(log n) | O(log n) | O(log n) | .1) | ? |
- ^ a b c d e f g h i Tiempo amortizado.
- ^ n es el tamaño del montón más grande.
- ^ Límite inferior de Ω Ω ()log log n),{displaystyle Omega (log log n),} límite superior O()22log log n).{displaystyle O(2^{2{sqrt {log log n}}}}
- ^ Brodal y Okasaki describen más adelante una variante persistente con los mismos límites excepto la tecla de reducción, que no es compatible. Saltos con n elementos pueden ser construidos en el fondo O()n).
Equivalencia de colas de prioridad y algoritmos de clasificación
Usando una cola de prioridad para ordenar
La semántica de las colas de prioridad sugiere naturalmente un método de clasificación: inserte todos los elementos que se van a clasificar en una cola de prioridad y elimínelos secuencialmente; saldrán en orden ordenado. Este es en realidad el procedimiento utilizado por varios algoritmos de clasificación, una vez que se elimina la capa de abstracción proporcionada por la cola de prioridad. Este método de clasificación es equivalente a los siguientes algoritmos de clasificación:
| Nombre | Aplicación de las colas prioritarias | Mejor | Promedio | peor |
|---|---|---|---|---|
| Heapsort | Heap | nlog ()n){displaystyle nlog(n)} | nlog ()n){displaystyle nlog(n)} | nlog ()n){displaystyle nlog(n)} |
| Smoothsort | Leonardo Heap | n{displaystyle n} | nlog ()n){displaystyle nlog(n)} | nlog ()n){displaystyle nlog(n)} |
| Tipo de selección | Array sin orden | n2{displaystyle n^{2} | n2{displaystyle n^{2} | n2{displaystyle n^{2} |
| Tipo de inserción | Ordenado Array | n{displaystyle n} | n2{displaystyle n^{2} | n2{displaystyle n^{2} |
| Árboles | Árbol de búsqueda binaria autodidacta | nlog ()n){displaystyle nlog(n)} | nlog ()n){displaystyle nlog(n)} | nlog ()n){displaystyle nlog(n)} |
Usando un algoritmo de clasificación para hacer una cola de prioridad
También se puede usar un algoritmo de clasificación para implementar una cola de prioridad. Específicamente, Thorup dice:
Presentamos una reducción general del espacio lineal determinista de las colas prioritarias para clasificar implicando que si podemos ordenar hasta n llaves S()n) tiempo por clave, entonces hay una cola de prioridad apoyando Borrador y insertar dentro O()S()n) tiempo y find-min en tiempo constante.
Es decir, si hay un algoritmo de clasificación que puede clasificar en tiempo O(S) por tecla, donde S es alguna función de n y tamaño de palabra, entonces uno puede usar el procedimiento dado para crear una cola de prioridad donde extraer el elemento de mayor prioridad es O(1) tiempo e insertar nuevos elementos (y eliminar elementos) es tiempo O(S). Por ejemplo, si uno tiene un algoritmo de clasificación O(n log n), puede crear una cola de prioridad con O(1) tirando e insertando O(log n).
Bibliotecas
A menudo se considera que una cola de prioridad es una "estructura de datos de contenedor".
La biblioteca de plantillas estándar (STL) y el estándar C++ 1998 especifican std::priority_queue como una de las plantillas de clase de adaptador de contenedor STL. Sin embargo, no especifica cómo se deben servir dos elementos con la misma prioridad y, de hecho, las implementaciones comunes no los devolverán según su orden en la cola. Implementa una cola de prioridad máxima y tiene tres parámetros: un objeto de comparación para ordenar, como un objeto de función (predeterminado en less<T> si no se especifica), el contenedor subyacente para almacenar las estructuras de datos (predeterminado en std::vector<T>) y dos iteradores al principio y al final de una secuencia. A diferencia de los contenedores STL reales, no permite la iteración de sus elementos (se adhiere estrictamente a su definición de tipo de datos abstractos). STL también tiene funciones de utilidad para manipular otro contenedor de acceso aleatorio como un montón máximo binario. Las bibliotecas de Boost también tienen una implementación en el montón de bibliotecas.
El módulo heapq de Python implementa un montón mínimo binario encima de una lista.
La biblioteca de Java contiene una clase PriorityQueue, que implementa una cola de prioridad mínima.
La biblioteca de.NET contiene una clase PriorityQueue, que implementa un montón mínimo cuaternario respaldado por una matriz.
La biblioteca de Scala contiene una clase PriorityQueue, que implementa una cola de máxima prioridad.
La biblioteca de Go contiene un módulo contenedor/montón, que implementa un montón mínimo sobre cualquier estructura de datos compatible.
La extensión de la biblioteca PHP estándar contiene la clase SplPriorityQueue.
El marco Core Foundation de Apple contiene una estructura CFBinaryHeap, que implementa un montón mínimo.
Aplicaciones
Gestión de ancho de banda
La cola de prioridad se puede usar para administrar recursos limitados, como el ancho de banda en una línea de transmisión desde un enrutador de red. En el caso de que el tráfico saliente quede en cola debido a un ancho de banda insuficiente, todas las demás colas se pueden detener para enviar el tráfico desde la cola de mayor prioridad al llegar. Esto garantiza que el tráfico priorizado (como el tráfico en tiempo real, por ejemplo, un flujo RTP de una conexión VoIP) se reenvía con la menor demora y la menor probabilidad de ser rechazado debido a que una cola alcanza su capacidad máxima. El resto del tráfico se puede manejar cuando la cola de prioridad más alta está vacía. Otro enfoque utilizado es enviar un tráfico desproporcionadamente mayor desde las colas de mayor prioridad.
Muchos protocolos modernos para redes de área local también incluyen el concepto de colas de prioridad en la subcapa de control de acceso a medios (MAC) para garantizar que las aplicaciones de alta prioridad (como VoIP o IPTV) experimenten una latencia más baja que otras aplicaciones que pueden ser servido con el servicio de mejor esfuerzo. Los ejemplos incluyen IEEE 802.11e (una enmienda a IEEE 802.11 que brinda calidad de servicio) y ITU-T G.hn (un estándar para redes de área local de alta velocidad que utiliza cableado doméstico existente (líneas eléctricas, líneas telefónicas y cables coaxiales).
Por lo general, se establece una limitación (policer) para limitar el ancho de banda que puede tomar el tráfico de la cola de mayor prioridad, a fin de evitar que los paquetes de alta prioridad bloqueen el resto del tráfico. Por lo general, este límite nunca se alcanza debido a instancias de control de alto nivel, como Cisco Callmanager, que se puede programar para inhibir llamadas que superen el límite de ancho de banda programado.
Simulación de eventos discretos
Otro uso de una cola de prioridad es administrar los eventos en una simulación de eventos discretos. Los eventos se agregan a la cola con su tiempo de simulación utilizado como prioridad. La ejecución de la simulación procede tirando repetidamente de la parte superior de la cola y ejecutando el evento allí.
Ver también: Programación (informática), teoría de colas
Algoritmo de Dijkstra
Cuando el gráfico se almacena en forma de lista de adyacencia o matriz, la cola de prioridad se puede usar para extraer el mínimo de manera eficiente al implementar el algoritmo de Dijkstra, aunque también se necesita la capacidad de alterar la prioridad de un vértice en particular en la cola de prioridad de manera eficiente.
Si, en cambio, un gráfico se almacena como objetos de nodo y los pares de prioridad-nodo se insertan en un montón, no es necesario alterar la prioridad de un vértice en particular si se rastrean los nodos visitados. Una vez que se visita un nodo, si vuelve a aparecer en el montón (habiendo tenido un número de prioridad más bajo asociado anteriormente), se elimina y se ignora.
Codificación Huffman
La codificación de Huffman requiere que uno obtenga repetidamente los dos árboles de frecuencia más baja. Una cola de prioridad es un método para hacer esto.
Algoritmos de búsqueda mejor primero
Los algoritmos de búsqueda Best-first, como el algoritmo de búsqueda A*, encuentran la ruta más corta entre dos vértices o nodos de un gráfico ponderado y prueban primero las rutas más prometedoras. Se utiliza una cola de prioridad (también conocida como margen) para realizar un seguimiento de las rutas no exploradas; aquél para el que la estimación (un límite inferior en el caso de A*) de la longitud total del trayecto es menor recibe la máxima prioridad. Si las limitaciones de memoria hacen que la búsqueda del mejor primero no sea práctica, se pueden usar variantes como el algoritmo SMA*, con una cola de prioridad doble para permitir la eliminación de elementos de baja prioridad.
Algoritmo de triangulación ROAM
El algoritmo de mallas de adaptación óptima en tiempo real (ROAM) calcula una triangulación dinámicamente cambiante de un terreno. Funciona dividiendo triángulos donde se necesitan más detalles y fusionándolos donde se necesitan menos detalles. El algoritmo asigna una prioridad a cada triángulo en el terreno, generalmente relacionada con la disminución del error si ese triángulo se dividiera. El algoritmo utiliza dos colas de prioridad, una para triángulos que se pueden dividir y otra para triángulos que se pueden fusionar. En cada paso, el triángulo de la cola dividida con la prioridad más alta se divide, o el triángulo de la cola de fusión con la prioridad más baja se fusiona con sus vecinos.
Algoritmo de Prim para árbol de expansión mínimo
Usando la cola de prioridad de pila mínima en el algoritmo de Prim para encontrar el árbol de expansión mínimo de un gráfico conectado y no dirigido, se puede lograr un buen tiempo de ejecución. Esta cola de prioridad de montón mínimo utiliza la estructura de datos de montón mínimo que admite operaciones como insertar, mínimo, extract-min, decrease- llave. En esta implementación, el peso de los bordes se usa para decidir la prioridad de los vértices. Menor peso, mayor prioridad y mayor peso, menor prioridad.
Cola de prioridad paralela
La paralización puede utilizarse para acelerar las colas prioritarias, pero requiere algunos cambios en la interfaz de cola prioritaria. La razón de tales cambios es que una actualización secuencial generalmente sólo tiene O()1){textstyle O(1)} o O()log n){textstyle O(log n)} costo, y no hay ganancia práctica para paralelizar tal operación. Un cambio posible es permitir el acceso simultáneo de varios procesadores a la misma cola prioritaria. El segundo cambio posible es permitir operaciones por lotes que funcionan k{textstyle k} elementos, en lugar de un solo elemento. Por ejemplo, ExtractoMin quitará la primera k{textstyle k} elementos con la máxima prioridad.
Acceso paralelo concurrente
Si la cola de prioridad permite el acceso simultáneo, varios procesos pueden realizar operaciones simultáneamente en esa cola de prioridad. Sin embargo, esto plantea dos cuestiones. En primer lugar, la definición de la semántica de las operaciones individuales ya no es obvia. Por ejemplo, si dos procesos quieren extraer el elemento con mayor prioridad, ¿deberían obtener el mismo elemento o elementos diferentes? Esto restringe el paralelismo en el nivel del programa que usa la cola de prioridad. Además, debido a que múltiples procesos tienen acceso al mismo elemento, esto lleva a la contención.
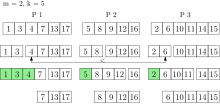
El acceso simultáneo a una cola de prioridad se puede implementar en un modelo PRAM de lectura y escritura simultáneas (CRCW). A continuación, la cola de prioridad se implementa como una lista de omisión. Además, se utiliza una primitiva de sincronización atómica, CAS, para hacer que la lista de saltos esté libre de bloqueos. Los nodos de la lista de omisión consisten en una clave única, una prioridad, una matriz de punteros, para cada nivel, a los siguientes nodos y una marca eliminar. La marca eliminar marca si el nodo está a punto de ser eliminado por un proceso. Esto asegura que otros procesos puedan reaccionar a la eliminación de manera apropiada.
- inserte e): Primero se crea un nuevo nodo con una clave y una prioridad. Además, el nodo se asigna una serie de niveles, que dicta el tamaño de la matriz de punteros. Luego se realiza una búsqueda para encontrar la posición correcta donde insertar el nuevo nodo. La búsqueda comienza desde el primer nodo y desde el nivel más alto. Luego la lista de saltos se atraviesa hasta el nivel más bajo hasta que se encuentre la posición correcta. Durante la búsqueda, para cada nivel el último nodo atravesado será salvado como nodo padre para el nuevo nodo en ese nivel. Además, el nodo al que el puntero, a ese nivel, del nodo padre apunta hacia, será salvado como el nodo sucesor del nuevo nodo a ese nivel. Después, para cada nivel del nuevo nodo, los punteros del nodo padre serán fijados al nuevo nodo. Por último, los punteros, por cada nivel, del nuevo nodo se establecerán a los nodos sucesores correspondientes.
- extracto-min: Primero, la lista de saltos se atraviesa hasta llegar a un nodo cuyo Borrador La marca no está lista. Esto Borrador La marca es que es verdad para ese nodo. Finalmente se actualizan los punteros de los nodos padres del nodo eliminado.
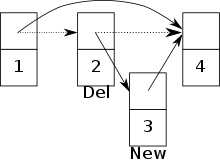
Si se permite el acceso simultáneo a una cola de prioridad, pueden surgir conflictos entre dos procesos. Por ejemplo, surge un conflicto si un proceso intenta insertar un nuevo nodo, pero al mismo tiempo otro proceso está a punto de eliminar el predecesor de ese nodo. Existe el riesgo de que el nuevo nodo se agregue a la lista de omisión, pero ya no se puede acceder a él. (Ver imagen)
Operaciones de elementos K
En este entorno, las operaciones en una cola de prioridad se generalizan a un lote de k{textstyle k} elementos. Por ejemplo, k_extract-min elimina los k{textstyle k} elementos más pequeños de la cola prioritaria y los devuelve.
En un entorno de memoria compartida, la cola de prioridad paralela puede implementarse fácilmente utilizando árboles de búsqueda binaria paralelos y algoritmos de árboles basados en la unión. En particular, k_extract-min corresponde a un división en el árbol de búsqueda binaria que tiene O()log n){textstyle O(log n)} cuesta y produce un árbol que contiene el k{textstyle k} elementos más pequeños. k_insert puede ser aplicado por un sindicato de la cola de prioridad original y el lote de las inserciones. Si el lote ya está arreglado por la llave, k_insert tiene O()klog ()1+nk)){textstyle O(klog(1+{frac {n}})} costo. De lo contrario, necesitamos ordenar primero el lote, así que el costo será O()klog ()1+nk)+klog k)=O()klog n){textstyle O(klog(1+{frac [n}{k})+klog k)=O(klog n)}. Otras operaciones para la cola prioritaria se pueden aplicar de manera similar. Por ejemplo, k_decrease-key se puede hacer por primera aplicación diferencia y luego sindicato, que primero elimina los elementos y luego los inserta de nuevo con las teclas actualizadas. Todas estas operaciones son muy paralelas, y la eficiencia teórica y práctica se puede encontrar en documentos de investigación relacionados.
El resto de esta sección analiza un algoritmo basado en colas en memoria distribuida. Suponemos que cada procesador tiene su propia memoria local y una cola de prioridad local (secuencial). Los elementos de la cola de prioridad global (paralela) se distribuyen entre todos los procesadores.
Una operación k_insert asigna los elementos uniformemente al azar a los procesadores que insertan los elementos en sus colas locales. Tenga en cuenta que aún se pueden insertar elementos individuales en la cola. Usando esta estrategia, los elementos más pequeños globales están en la unión de los elementos más pequeños locales de cada procesador con alta probabilidad. Así, cada procesador tiene una parte representativa de la cola de prioridad global.
Esta propiedad se utiliza cuando k_extract-min es ejecutado, como el más pequeño m{textstyle m} elementos de cada cola local se eliminan y se recogen en un conjunto de resultados. Los elementos del conjunto de resultados siguen asociados con su procesador original. Número de elementos m{textstyle m} que se elimina de cada cola local depende de k{textstyle k} y el número de procesadores p{textstyle p}. Selección paralela k{textstyle k} se determinan los elementos más pequeños del conjunto de resultados. Con alta probabilidad estos son el mundo k{textstyle k} elementos más pequeños. Si no, m{textstyle m} Los elementos se retiran de cada cola local y se ponen en el conjunto de resultados. Esto se hace hasta que el mundo k{textstyle k} los elementos más pequeños están en el conjunto de resultados. Ahora k{textstyle k} los elementos pueden ser devueltos. Todos los demás elementos del conjunto de resultados se insertan en sus colas locales. El tiempo de funcionamiento k_extract-min se espera O()kplog ()n)){textstyle O({frac {k}{p}log(n)}, donde k=Ω Ω ()p⋅ ⋅ log ()p)){textstyle k=Omega (pcdot log(p)} y n{textstyle n} es el tamaño de la cola de prioridad.
La cola de prioridad se puede mejorar aún más al no mover los elementos restantes del conjunto de resultados directamente a las colas locales después de una operación k_extract-min. Esto ahorra elementos en movimiento de un lado a otro todo el tiempo entre el conjunto de resultados y las colas locales.
Al eliminar varios elementos a la vez se puede alcanzar una velocidad considerable. Pero no todos los algoritmos pueden usar este tipo de cola prioritaria. El algoritmo de Dijkstra, por ejemplo, no puede funcionar en varios nodos a la vez. El algoritmo toma el nodo con la distancia más pequeña de la cola de prioridad y calcula nuevas distancias para todos sus nodos vecinos. Si te fueras k{textstyle k} nodos, trabajar en un nodo podría cambiar la distancia de otro de los k{textstyle k} nodos. Así que el uso de operaciones de k-element destruye la propiedad de configuración de etiquetas del algoritmo de Dijkstra.
Contenido relacionado
Dorado de alta potencia
Registro de desplazamiento de retroalimentación lineal
MIRC