Coeficientes de einstein

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Cuantidades que describen la probabilidad de absorción o emisión de luz

En física atómica, molecular y óptica, los coeficientes de Einstein son cantidades que describen la probabilidad de absorción o emisión de un fotón por un átomo o molécula. Los coeficientes A de Einstein están relacionados con la tasa de emisión espontánea de luz, y los coeficientes B de Einstein están relacionados con la absorción y emisión estimulada de luz. A lo largo de este artículo, "luz" Se refiere a cualquier radiación electromagnética, no necesariamente en el espectro visible.

Estos coeficientes llevan el nombre de Albert Einstein, quien los propuso en 1916.

Líneas espectrales

En física, uno piensa en una línea espectral desde dos puntos de vista.

Una línea de emisión se forma cuando un átomo o molécula hace una transición desde un nivel de energía discreto particular $E 2$ de un átomo, a un nivel de energía inferior $E 1$ , emitiendo un fotón de una energía y longitud de onda particular. Un espectro de muchos de estos fotones mostrará un pico de emisión en la longitud de onda asociada con estos fotones.

Una línea de absorción se forma cuando un átomo o molécula hace una transición desde un $E 1$ inferior, a un estado de energía discreta superior, $E 2$ , con un fotón absorbido en el proceso. Estos fotones absorbidos generalmente provienen de la radiación continua de fondo (el espectro completo de la radiación electromagnética) y un espectro mostrará una caída en la radiación continua en la longitud de onda asociada con los fotones absorbidos.

Los dos estados deben ser estados ligados en los que el electrón está unido al átomo o molécula, por lo que a veces se hace referencia a la transición como una transición "unida-unida" transición, a diferencia de una transición en la que el electrón es expulsado completamente del átomo (transición "ligado-libre") a un estado continuo, dejando un átomo ionizado y generando radiación continua.

Un fotón con una energía igual a la diferencia $E 2 - E 1$ entre los niveles de energía se libera o absorbe en el proceso. La frecuencia $ν$ a la que se produce la línea espectral está relacionada con la energía del fotón mediante la condición de frecuencia de Bohr $E 2 - E 1 = hν$ donde h denota la constante de Planck.

Coeficientes de emisión y absorción

Una línea espectral atómica se refiere a eventos de emisión y absorción en un gas en el que ${displaystyle n_{2}}$ es la densidad de los átomos en el estado de energía superior para la línea, y ${displaystyle n_{1}}$ es la densidad de los átomos en el estado de baja energía para la línea.

La emisión de radiación de la línea atómica a frecuencia $.$ puede describirse por un coeficiente de emisión ${displaystyle varepsilon }$ con unidades de energía/(tiempo × volumen × ángulo sólido). ε ♪ dV dΩ es entonces la energía emitida por un elemento de volumen ${displaystyle dV}$ en el tiempo ${displaystyle dt}$ en ángulo sólido ${displaystyle dOmega }$ . Para la radiación de la línea atómica,

{displaystyle varepsilon ={frac {hnu }{4pi }}n_{2}A_{21},}

{displaystyle A_{21}}

La absorción de la radiación de la línea atómica puede describirse por un coeficiente de absorción ${displaystyle kappa }$ con unidades de 1 / longitud. La expresión κ' dx da la fracción de intensidad absorbida para un rayo de luz a frecuencia $.$ mientras viaja distancia dx. El coeficiente de absorción es dado por

{displaystyle kappa '={frac {hnu }{4pi }}(n_{1}B_{12}-n_{2}B_{21}),}

{displaystyle B_{12}}

{displaystyle B_{21}}

{displaystyle A_{21}}

{displaystyle B_{12}}

{displaystyle B_{21}}

Las ecuaciones anteriores han ignorado la influencia de la forma de la línea espectroscópica. Para ser precisos, las ecuaciones anteriores deben multiplicarse por la forma de la línea espectral (normalizada), en cuyo caso las unidades cambiarán para incluir un término de 1/Hz.

En condiciones de equilibrio termodinámico, el número de densidades ${displaystyle n_{2}}$ y ${displaystyle n_{1}}$ , los coeficientes de Einstein, y la densidad de energía espectral proporcionan suficiente información para determinar las tasas de absorción y emisión.

Condiciones de equilibrio

El número de densidades ${displaystyle n_{2}}$ y ${displaystyle n_{1}}$ son fijados por el estado físico del gas en el que se produce la línea espectral, incluyendo el radiante espectral local (o, en algunas presentaciones, la densidad de energía radiante espectral local). Cuando ese estado es uno de los equilibrios termodinámicos estrictos, o uno de los llamados "equilibrio termodinámico local", entonces la distribución de estados atómicos de excitación (que incluye ${displaystyle n_{2}}$ y ${displaystyle n_{1}}$ ) determina las tasas de emisiones atómicas y absorción para ser tal que la ley de Kirchhoff de igualdad de la absorción radiativa y la emisividad sostiene. En estricto equilibrio termodinámico, se dice que el campo de radiación es la radiación del cuerpo negro y se describe por la ley de Planck. Para el equilibrio termodinámico local, el campo de radiación no tiene que ser un campo de cuerpo negro, pero la tasa de colisiones interatómicas debe exceder enormemente las tasas de absorción y emisión de quanta de luz, de modo que las colisiones interatómicas dominan por completo la distribución de estados de excitación atómica. Las circunstancias ocurren en las que el equilibrio termodinámico local no prevalece, porque los fuertes efectos radiativos abruman la tendencia a la distribución Maxwell-Boltzmann de velocidades moleculares. Por ejemplo, en la atmósfera del Sol predomina la gran fuerza de la radiación. En la atmósfera superior de la Tierra, a altitudes superiores a 100 km, la rareza de las colisiones intermoleculares es decisiva.

En los casos de equilibrio termodinámico y de equilibrio termodinámico local, las densidades numéricas de los átomos, tanto excitados como no excitados, pueden calcularse a partir de la distribución de Maxwell-Boltzmann, pero para otros casos (por ejemplo, láseres) el cálculo es más complicado.

Coeficientes de Einstein

En 1916, Albert Einstein propuso que hay tres procesos que ocurren en la formación de una línea espectral atómica. Los tres procesos se denominan emisión espontánea, emisión estimulada y absorción. A cada uno se le asocia un coeficiente de Einstein, que es una medida de la probabilidad de que ocurra ese proceso en particular. Einstein consideró el caso de la radiación isotrópica de frecuencia $ν$ y densidad de energía espectral $ρ (ν)$ . Paul Dirac derivó los coeficientes en un artículo de 1927 titulado "La teoría cuántica de la emisión y absorción de radiación".

Varias formulaciones

Hilborn ha comparado varias formulaciones para derivaciones de los coeficientes de Einstein, de varios autores. Por ejemplo, Herzberg trabaja con irradiancia y número de onda; Yariv trabaja con energía por unidad de volumen por unidad de intervalo de frecuencia, como es el caso en la formulación más reciente (2008). Mihalas & Weibel-Mihalas trabaja con resplandor y frecuencia; también Chandrasekhar; también Goody & Yung; Loudon utiliza frecuencia angular y resplandor.

Emisión espontánea

La emisión espontánea es el proceso por el cual un electrón "espontáneo" (es decir, sin ninguna influencia externa) decae de un nivel de energía superior a uno inferior. El proceso es descrito por el coeficiente de Einstein A₂₁ ()s⁻¹), que da la probabilidad por unidad tiempo que un electrón en estado 2 con energía ${displaystyle E_{2}}$ decaerá espontáneamente al estado 1 con energía ${displaystyle E_{1}}$ , emitiendo un fotón con una energía $E 2 - E 1 = .$ . Debido al principio de incertidumbre de tiempo energético, la transición realmente produce fotones dentro de una gama estrecha de frecuencias llamadas el ancho de línea espectral. Si ${displaystyle n_{i}}$ es la densidad número de átomos en estado i entonces el cambio en la densidad número de átomos en estado 2 por unidad tiempo debido a la emisión espontánea será

{displaystyle left({frac {dn_{2}}{dt}}right)_{text{spontaneous}}=-A_{21}n_{2}.}

El mismo proceso resulta en el aumento de la población del estado 1:

{displaystyle left({frac {dn_{1}}{dt}}right)_{text{spontaneous}}=A_{21}n_{2}.}

Emisión estimulada

La emisión estimulada (también conocida como emisión inducida) es el proceso por el cual se induce a un electrón a saltar de un nivel de energía superior a uno inferior por la presencia de radiación electromagnética en (o cerca) la frecuencia de la transición. Desde el punto de vista termodinámico, este proceso debe considerarse como una absorción negativa. El proceso es descrito por el coeficiente de Einstein ${displaystyle B_{21}}$ (m³ J⁻¹ s⁻²), que da la probabilidad por tiempo unitario por densidad de energía unitaria del campo de radiación por frecuencia unitaria que un electrón en estado 2 con energía ${displaystyle E_{2}}$ decaimiento al estado 1 con energía ${displaystyle E_{1}}$ , emitiendo un fotón con una energía $E 2 - E 1 = .$ . El cambio en la densidad número de átomos en el estado 1 por unidad de tiempo debido a la emisión inducida será

{displaystyle left({frac {dn_{1}}{dt}}right)_{text{neg. absorb.}}=B_{21}n_{2}rho (nu),}

{displaystyle rho (nu)}

La emisión estimulada es uno de los procesos fundamentales que llevaron al desarrollo del láser. Sin embargo, la radiación láser está muy lejos del caso actual de la radiación isotrópica.

Absorción de fotones

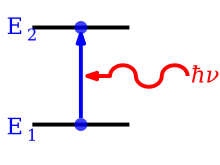
La absorción es el proceso por el cual un fotón es absorbido por el átomo, causando que un electrón salte de un nivel de energía inferior a uno más alto. El proceso es descrito por el coeficiente de Einstein ${displaystyle B_{12}}$ (m³ J⁻¹ s⁻²), que da la probabilidad por tiempo unitario por densidad de energía unitaria del campo de radiación por frecuencia unitaria que un electrón en estado 1 con energía ${displaystyle E_{1}}$ absorberá un fotón con una energía $E 2 - E 1 = .$ y saltar al estado 2 con energía ${displaystyle E_{2}}$ . El cambio en la densidad número de átomos en el estado 1 por unidad de tiempo debido a la absorción será

{displaystyle left({frac {dn_{1}}{dt}}right)_{text{pos. absorb.}}=-B_{12}n_{1}rho (nu).}

Equilibrio detallado

Los coeficientes de Einstein son probabilidades fijas por tiempo asociadas a cada átomo, y no dependen del estado del gas del que forman parte los átomos. Por lo tanto, cualquier relación que podamos derivar entre los coeficientes en, digamos, equilibrio termodinámico será válida universalmente.

En el equilibrio termodinámico, tendremos un equilibrio simple, en el que el cambio neto en el número de átomos excitados es cero, y se equilibra con las pérdidas y ganancias debidas a todos los procesos. Con respecto a las transiciones ligadas, también tendremos un equilibrio detallado, que establece que el intercambio neto entre dos niveles cualesquiera estará equilibrado. Esto se debe a que las probabilidades de transición no pueden verse afectadas por la presencia o ausencia de otros átomos excitados. El equilibrio detallado (válido sólo en equilibrio) requiere que el cambio en el tiempo del número de átomos en el nivel 1 debido a los tres procesos anteriores sea cero:

{displaystyle 0=A_{21}n_{2}+B_{21}n_{2}rho (nu)-B_{12}n_{1}rho (nu).}

Junto con el equilibrio detallado, a una temperatura $T$ podemos utilizar nuestro conocimiento de la distribución de energía en equilibrio de los átomos, como se establece en Maxwell– Distribución de Boltzmann y distribución de equilibrio de los fotones, como se establece en la ley de radiación del cuerpo negro de Planck para derivar relaciones universales entre los coeficientes de Einstein.

De la distribución de Boltzmann tenemos para el número de especies atómicas excitadas i:

{displaystyle {frac {n_{i}}{n}}={frac {g_{i}e^{-E_{i}/kT}}{Z}},}

nkT

{displaystyle g_{i}}

T

.

{displaystyle rho _{nu }(nuT)=F(nu){frac {1}{e^{hnu /kT}-1}},}

{displaystyle F(nu)={frac {2hnu ^{3}}{c^{2}}},}

{displaystyle c}

{displaystyle h}

Sustituyendo estas expresiones en la ecuación de equilibrio detallado y recordando que $E 2 - E 1 = hν$ rendimientos

{displaystyle A_{21}g_{2}e^{-hnu /kT}+B_{21}g_{2}e^{-hnu /kT}{frac {F(nu)}{e^{hnu /kT}-1}}=B_{12}g_{1}{frac {F(nu)}{e^{hnu /kT}-1}},}

{displaystyle A_{21}g_{2}(1-e^{-hnu /kT})+B_{21}g_{2}F(nu)e^{-hnu /kT}=B_{12}g_{1}F(nu).}

La ecuación anterior debe mantener a cualquier temperatura, así que desde ${displaystyle Tto infty }$ uno se pone

{displaystyle B_{21}g_{2}=B_{12}g_{1},}

{displaystyle Tto 0}

{displaystyle A_{21}g_{2}=B_{21}g_{2}F(nu).}

Por lo tanto, los tres coeficientes de Einstein están interrelacionados por

{displaystyle {frac {A_{21}}{B_{21}}}=F(nu)}

{displaystyle {frac {B_{21}}{B_{12}}}={frac {g_{1}}{g_{2}}}.}

Cuando esta relación se inserta en la ecuación original, también se puede encontrar una relación entre ${displaystyle A_{21}}$ y ${displaystyle B_{12}}$ , implicando la ley de Planck.

Fortalezas del oscilador

La fuerza osciladora ${displaystyle f_{12}}$ se define por la siguiente relación con la sección transversal ${displaystyle sigma }$ para la absorción:

{displaystyle sigma ={frac {e^{2}}{4varepsilon _{0}m_{e}c}},f_{12},phi _{nu }={frac {pi e^{2}}{2varepsilon _{0}m_{e}c}},f_{12},phi _{omega },}

Donde ${displaystyle e}$ es la carga de electrones, ${displaystyle m_{e}}$ es la masa de electrones, y ${displaystyle phi _{nu }}$ y ${displaystyle phi _{omega }}$ son funciones de distribución normalizadas en frecuencia y frecuencia angular respectivamente. Esto permite que los tres coeficientes de Einstein se expresen en términos de la fuerza de oscilador único asociado con la línea espectral atómica particular:

{displaystyle {begin{aligned}B_{12}&={frac {e^{2}}{4varepsilon _{0}m_{e}hnu }}f_{12},\[1ex]B_{21}&={frac {e^{2}}{4varepsilon _{0}m_{e}hnu }}{frac {g_{1}}{g_{2}}}f_{12},\[1ex]A_{21}&={frac {2pi nu ^{2}e^{2}}{varepsilon _{0}m_{e}c^{3}}}{frac {g_{1}}{g_{2}}}f_{12}.end{aligned}}}

Aproximación dipolo

El valor de los coeficientes A y B se puede calcular utilizando la mecánica cuántica, donde se utilizan aproximaciones dipolares en la teoría de perturbaciones dependientes del tiempo. Si bien el cálculo del coeficiente B se puede realizar fácilmente, el del coeficiente A requiere utilizar los resultados de la segunda cuantificación. Esto se debe a que la teoría desarrollada por la aproximación dipolar y la teoría de la perturbación dependiente del tiempo da una descripción semiclásica de la transición electrónica que llega a cero cuando los campos perturbadores llegan a cero. El coeficiente A que gobierna la emisión espontánea no debería llegar a cero, ya que los campos perturbadores llegan a cero. El resultado para tasas de transición de diferentes niveles electrónicos como resultado de una emisión espontánea se da como (en unidades SI):

{displaystyle w_{ito f}^{text{s.emi}}={frac {omega _{if}^{3}e^{2}}{3pi varepsilon _{0}hbar c^{3}}}left|langle f|{vec {r}}|irangle right|^{2}=A_{if}}

Para el coeficiente B, la aplicación directa de la aproximación dipolar en la teoría de la perturbación dependiente del tiempo produce (en unidades SI):

{displaystyle w_{irightarrow f}^{text{abs}}={frac {u(omega _{fi})pi e^{2}}{3varepsilon _{0}hbar ^{2}}}left|langle f|{vec {r}}|irangle right|^{2}=B_{if}^{text{abs}}u(omega _{fi})}

{displaystyle w_{ito f}^{text{emi}}={frac {u(omega _{if})pi e^{2}}{3varepsilon _{0}hbar ^{2}}}left|langle f|{vec {r}}|irangle right|^{2}=B_{if}^{emi}u(omega _{if})}

Tenga en cuenta que la fórmula de velocidad de transición depende del operador del momento dipolar. Para aproximaciones de orden superior, se trata de momento cuadrupolar y otros términos similares.

Aquí, los coeficientes B son elegidos para corresponder a ${displaystyle omega }$ función de distribución de energía. A menudo estas diferentes definiciones de coeficientes B se distinguen por superscript, por ejemplo, ${textstyle B_{21}^{f}={frac {B_{21}^{omega }}{2pi }}}$ Donde ${textstyle B_{21}^{f}}$ término corresponde a distribución de frecuencias y ${textstyle B_{21}^{omega }}$ término corresponde a ${displaystyle omega }$ distribución. Las fórmulas para los coeficientes B varían inversamente a la de la distribución de energía elegida, de modo que la tasa de transición sea la misma independientemente de la convención.

Por lo tanto, los coeficientes AB se calculan utilizando la aproximación dipolar como:

{displaystyle {begin{aligned}A_{ab}&={frac {omega _{ab}^{3}e^{2}}{3pi varepsilon _{0}hbar c^{3}}}left|langle a|{vec {r}}|brangle right|^{2}\[1ex]B_{ab}&={frac {pi e^{2}}{3varepsilon _{0}hbar ^{2}}}left|langle a|{vec {r}}|brangle right|^{2}end{aligned}}}

{displaystyle omega _{ab}={frac {E_{a}-E_{b}}{hbar }}}

{displaystyle omega }

De ahí que también se deriven las siguientes proporciones:

{displaystyle {frac {B_{12}}{B_{21}}}=1}

{displaystyle {frac {A_{if}}{B}}={frac {omega _{if}^{3}hbar }{pi ^{2}c^{3}}}}

Derivación de la ley de Planck

De la teoría se desprende que:

{displaystyle {frac {dN_{b}}{dt}}=-A_{ba}N_{b}-N_{b}u(omega _{ba})B_{ba}+N_{a}u(omega _{ba})B_{ab}=-N_{b}w_{bto a}^{text{s.emi}}-N_{b}w_{bto a}^{text{emi}}+N_{a}w_{ato b}^{text{abs}}}

{displaystyle N_{a}}

{displaystyle N_{b}}

{displaystyle E_{a}}

{displaystyle E_{b}}

E_{a}}" xmlns="http://www.w3.org/1998/Math/MathML">Eb■Ea{displaystyle E_{b}E_{a}}" aria-hidden="true" class="mwe-math-fallback-image-inline mw-invert" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/0059501ffeaff0420c6c2d2c8704acef9a3c726e" style="vertical-align: -0.671ex; width:8.568ex; height:2.509ex;"/>

{displaystyle omega }

{displaystyle omega _{ba}}

Donde la distribución Maxwell implica ${displaystyle N_{a}}$ y ${displaystyle N_{b}}$ garantías ${displaystyle {frac {N_{a}}{N_{b}}}={frac {e^{-E_{a}beta }}{e^{-E_{b}beta }}}=e^{omega _{ba}hbar beta }}$

Solving for ${displaystyle u}$ para la condición de equilibrio ${displaystyle {frac {dN_{b}}{dt}}=0}$ utilizando las ecuaciones y ratios anteriores al tiempo que se generaliza ${displaystyle omega _{ba}}$ a ${displaystyle omega }$ , tenemos:

{displaystyle u_{omega }(omegaT)={frac {omega ^{3}hbar }{pi ^{2}c^{3}}}{frac {1}{e^{omega hbar beta }-1}}}

Otra lectura

Condon, E. U.; Shortley, G. H. (1964). The The The Theory of Atomic Spectra. Cambridge University Press. ISBN 0-521-09209-4.
Rybicki, G. B.; Lightman, A. P. (1985). Procesos radiativos en Astrofísica. John Wiley & Sons, Nueva York. ISBN 0-471-82759-2.
Shu, F. H. (1991). La Física de la Astrofísica. Vol. 1: Radiación. University Science Books, Mill Valley, CA. ISBN 0-935702-64-4.
Robert C. Hilborn (2002). "Coeficientes Einstein, secciones transversales, valores f, momentos dipoles y todo eso". Am. J. Phys. 50: 982-986. arXiv:física/0202029.
Taylor, M. A.; Vilchez, J. M. (2009). "Tutorial: Examinar soluciones para las poblaciones del ión n-nivel". Publicaciones de la Sociedad Astronómica del Pacífico. 121 (885): 1257–1266. arXiv:0709.3473. Bibcode:2009PASP..121.1257T. doi:10.1086/648121. S2CID 16116964.

Contenido relacionado

Más resultados...