Coeficiente GINI

ImprimirCitar

Medición de la desigualdad en la distribución de ingresos o riqueza

Mapa mundial de la desigualdad de ingresos Coeficientes Gini por país (como %). Sobre la base de datos del Banco Mundial desde 1992 hasta 2020.

Por encima de 50
Entre 45 y 50
Entre 40 y 45
Entre 35 y 40
Entre 30 y 35
A continuación 30
No hay datos

Un mapa que muestra coeficientes Gini para la riqueza dentro de los países para 2019

Global share of wealth by wealth group. Redrawn de datos de Credit Suisse, 2021

En economía, el coeficiente de Gini (JEE-nee), también conocido como índice de Gini o ratio de Gini, es una medida de dispersión estadística destinada a representar la desigualdad de ingresos o la desigualdad de riqueza dentro de una nación o un grupo social. El coeficiente de Gini fue desarrollado por el estadístico y sociólogo Corrado Gini.

El coeficiente de Gini mide la desigualdad entre los valores de una distribución de frecuencia, como los niveles de ingresos. Un coeficiente de Gini de 0 refleja igualdad perfecta, donde todos los valores de ingreso o riqueza son iguales, mientras que un coeficiente de Gini de 1 (o 100 %) refleja desigualdad máxima entre los valores. Por ejemplo, si todos tienen los mismos ingresos, el coeficiente de Gini será 0. En cambio, si para un gran número de personas solo una persona tiene todos los ingresos o consumos y todos los demás no tienen ninguno, el coeficiente de Gini será 1.

El coeficiente de Gini fue propuesto por Corrado Gini como una medida de la desigualdad de ingresos o riqueza. Para los países de la OCDE, a finales del siglo XX, considerando el efecto de los impuestos y los pagos de transferencias, el coeficiente de Gini de ingresos osciló entre 0,24 y 0,49, siendo Eslovenia el más bajo y México el más alto. Los países africanos tuvieron los coeficientes de Gini antes de impuestos más altos en 2008-2009, siendo Sudáfrica el más alto del mundo, estimado de diversas formas entre 0,63 y 0,7, aunque esta cifra se reduce a 0,52 después de tener en cuenta la asistencia social, y vuelve a caer a 0,47 después de impuestos. Varias fuentes estiman que el coeficiente de Gini del ingreso global en 2005 se encuentra entre 0,61 y 0,68.

Hay algunos problemas al interpretar un coeficiente de Gini; el mismo valor puede resultar de muchas curvas de distribución diferentes. Se debe tener en cuenta la estructura demográfica. Los países con una población que envejece o con una tasa de natalidad más alta experimentan un aumento del coeficiente de Gini antes de impuestos, incluso si la distribución del ingreso real para los adultos que trabajan permanece constante. Los estudiosos han ideado más de una docena de variantes del coeficiente de Gini.

Historia

El coeficiente de Gini fue desarrollado por el estadístico italiano Corrado Gini y publicado en su artículo de 1912 Variabilidad y mutabilidad (en italiano: Variabilità e mutabilità). Basándose en el trabajo del economista estadounidense Max Lorenz, Gini propuso que la diferencia entre la línea recta hipotética que representa la igualdad perfecta y la línea real que representa los ingresos de las personas se utilice como medida de la desigualdad.

Definición

Representación gráfica del coeficiente Gini:

El gráfico muestra que el coeficiente Gini es igual al área marcada A dividido por la suma de las áreas marcadas A y B, es decir, Gini = A/(A + B). También es igual a 2A y a 1 - 2B por el hecho de que A + B = 0,5 (desde la escala de ejes de 0 a 1).

El coeficiente de Gini es un índice del grado de desigualdad en la distribución de ingresos/riqueza, que se utiliza para estimar en qué medida la riqueza o la distribución de ingresos de un país se desvía de una distribución equitativa.

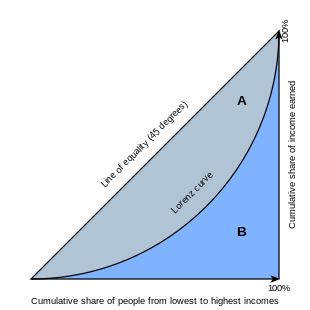
El coeficiente de Gini generalmente se define matemáticamente en función de la curva de Lorenz, que traza la proporción del ingreso total de la población (eje y) que gana acumulativamente la parte inferior x de la población. (ver diagrama). La línea de 45 grados representa así la perfecta igualdad de ingresos. Entonces, el coeficiente de Gini se puede considerar como la relación del área que se encuentra entre la línea de igualdad y la curva de Lorenz (marcada A en el diagrama) sobre el área total bajo la línea de igualdad (marcada A y B en el diagrama); es decir, G = A/(A + B). Si no hay ingresos negativos, también es igual a 2A y a 1 − 2B por el hecho que A + B = 0,5.

Supongamos que todas las personas tienen ingresos no negativos (o riqueza, según sea el caso). En ese caso, el coeficiente de Gini teóricamente puede variar de 0 (igualdad total) a 1 (desigualdad total) y, a veces, se expresa como un porcentaje que oscila entre 0 y 100. Si los valores negativos son posibles (como la riqueza de las personas con deudas), entonces, teóricamente, el coeficiente de Gini podría ser superior a 1. Por lo general, se supone que la media (o total) es positiva, lo que descarta un coeficiente de Gini inferior a cero.

Un enfoque alternativo es definir el coeficiente Gini como la mitad de la diferencia absoluta media relativa, que es matemáticamente equivalente a la definición basada en la curva Lorenz. La diferencia absoluta media es la diferencia absoluta promedio de todos los pares de elementos de la población, y la diferencia media absoluta relativa es la diferencia absoluta media dividida por el promedio, ${bar {x}}$ , normalizar para escala. Si x_i es la riqueza o el ingreso de la persona i, y hay n personas, luego el coeficiente Gini G es dado por:

{displaystyle G={frac {displaystyle {sum _{i=1}^{n}sum _{j=1}^{n}left|x_{i}-x_{j}right|}}{displaystyle {2sum _{i=1}^{n}sum _{j=1}^{n}x_{j}}}}={frac {displaystyle {sum _{i=1}^{n}sum _{j=1}^{n}left|x_{i}-x_{j}right|}}{displaystyle {2nsum _{j=1}^{n}x_{j}}}}={frac {displaystyle {sum _{i=1}^{n}sum _{j=1}^{n}left|x_{i}-x_{j}right|}}{displaystyle {2n^{2}{bar {x}}}}}}

Cuando la distribución de ingresos (o riqueza) se da como una función de densidad de probabilidad continua p(x), el coeficiente de Gini es nuevamente la mitad de la diferencia absoluta media relativa:

{displaystyle G={frac {1}{2mu }}int _{-infty }^{infty }int _{-infty }^{infty }p(x)p(y),|x-y|,dx,dy}

Donde ${displaystyle textstyle mu =int _{-infty }^{infty }xp(x),dx}$ es la media de la distribución, y los límites inferiores de la integración pueden ser reemplazados por cero cuando todos los ingresos son positivos.

Cálculo

Más rico u de la población (rojo) f de todos los ingresos o la riqueza; otros (verde) igualmente compartir restante: G = f − u. Una distribución lisa (azul) con la misma u y f siempre G ■ f − u.

Si bien la distribución del ingreso de cualquier país en particular no siempre seguirá modelos teóricos, en realidad, estos modelos brindan una comprensión cualitativa de la distribución del ingreso en una nación dado el coeficiente de Gini.

Ejemplo: dos niveles de ingresos

Los casos extremos están representados por los "más iguales" sociedad en la que todas las personas reciben los mismos ingresos (G = 0) y los "más desiguales" sociedad (compuesta por N individuos) donde una sola persona recibe el 100% de los ingresos totales y el resto N − 1 las personas no reciben ninguno (G = 1 − 1/N).

Un caso simplificado distingue solo dos niveles de ingreso, bajo y alto. Si el grupo de altos ingresos es una proporción u de la población y gana una proporción f de todos los ingresos, entonces el coeficiente de Gini es f − u. Una distribución más graduada con estos mismos valores u y f siempre tendrá un coeficiente de Gini más alto que f − u.

Un caso de ejemplo en el que el 20 % más rico de la población tenga el 80 % de todos los ingresos (consulte el principio de Pareto) daría lugar a un coeficiente de Gini de ingresos de al menos el 60 %.

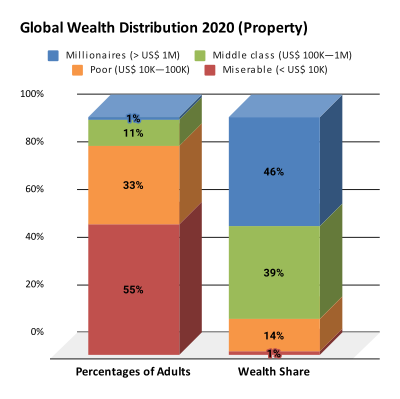
Otro caso de ejemplo en el que el 1 % de la población mundial posee el 50 % de toda la riqueza daría como resultado un coeficiente de Gini de riqueza de al menos el 49 %.

Expresiones alternativas

En algunos casos, esta ecuación se puede aplicar para calcular el coeficiente de Gini sin referencia directa a la curva de Lorenz. Por ejemplo, (tomando y para indicar los ingresos o la riqueza de una persona u hogar):

Para un uniforme de población sobre los valores Sí._i, i = 1 a n, indexado en orden no-disminución (Sí._i ≤ Sí._{i+ 1}):

{displaystyle G={frac {1}{n}}left(n+1-2left({frac {sum _{i=1}^{n}(n+1-i)y_{i}}{sum _{i=1}^{n}y_{i}}}right)right).}

Esto puede simplificarse para:

{displaystyle G={frac {2sum _{i=1}^{n}iy_{i}}{nsum _{i=1}^{n}y_{i}}}-{frac {n+1}{n}}.}

Esta fórmula realmente se aplica a cualquier población real, ya que cada persona puede ser asignada a su propio Sí._i.

Dado que el coeficiente de Gini es la mitad de la diferencia absoluta media relativa, también se puede calcular usando fórmulas para la diferencia absoluta media relativa. Para una muestra aleatoria S que consta de valores y_i, i = 1 a n, que están indexados en orden no decreciente (y_i ≤ y _i+1), la estadística:

{displaystyle G(S)={frac {1}{n-1}}left(n+1-2left({frac {sum _{i=1}^{n}(n+1-i)y_{i}}{sum _{i=1}^{n}y_{i}}}right)right)}

es un estimador consistente del coeficiente de Gini de la población, pero no es, en general, imparcial. Al igual que G, G(S) tiene una forma más simple:

{displaystyle G(S)=1-{frac {2}{n-1}}left(n-{frac {sum _{i=1}^{n}iy_{i}}{sum _{i=1}^{n}y_{i}}}right).}

No existe un estadístico muestral que sea, en general, un estimador insesgado del coeficiente de Gini poblacional, como la diferencia absoluta media relativa.

Distribución de probabilidad discreta

Para una distribución discreta de probabilidad con función de masa de probabilidad ${displaystyle f(y_{i}),}$ $i = 1,ldots, n$ , donde ${displaystyle f(y_{i})}$ es la fracción de la población con ingresos o riqueza $0}" xmlns="http://www.w3.org/1998/Math/MathML">Sí.i■0{displaystyle Y...0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/2000cdffbebd85d221d8cc0cc18738a220caf555" style="vertical-align: -0.671ex; width:6.2ex; height:2.509ex;"/>$ , el coeficiente Gini es:

{displaystyle G={frac {1}{2mu }}sum limits _{i=1}^{n}sum limits _{j=1}^{n},f(y_{i})f(y_{j})|y_{i}-y_{j}|}

dónde

{displaystyle mu =sum limits _{i=1}^{n}y_{i}f(y_{i}).}

Si los puntos con probabilidades no cero se indexan en orden creciente $<math alttext="{displaystyle (y_{i}()Sí.i.Sí.i+1){displaystyle (y_{i}traducido_{i+1}<img alt="{displaystyle (y_{i}$ , entonces:

{displaystyle G=1-{frac {sum _{i=1}^{n}f(y_{i})(S_{i-1}+S_{i})}{S_{n}}}}

dónde

{displaystyle S_{i}=sum _{j=1}^{i}f(y_{j}),y_{j},}

{displaystyle S_{0}=0.}

Estas fórmulas también son aplicables en el límite, como

{displaystyle nrightarrow infty.}

Distribución de probabilidad continua

Cuando la población es grande, la distribución del ingreso puede representarse mediante una función de densidad de probabilidad continua f(x) donde f(x) dx es la fracción de la población con riqueza o ingresos en el intervalo dx alrededor de x. Si F(x) es la función de distribución acumulativa para f(x):

{displaystyle F(x)=int _{0}^{x}f(x),dx}

y L(x) es la función de Lorenz:

{displaystyle L(x)={frac {int _{0}^{x}x,f(x),dx}{int _{0}^{infty }x,f(x),dx}}}

entonces la curva de Lorenz L(F) se puede representar como una función paramétrica en L(x) y F(x) y el valor de B se puede encontrar por integración:

{displaystyle B=int _{0}^{1}L(F),dF.}

El coeficiente de Gini también se puede calcular directamente a partir de la función de distribución acumulativa de la distribución F(y). Definiendo μ como la media de la distribución y especificando que F(y) es cero para todos los valores negativos, el coeficiente de Gini viene dado por:

{displaystyle G=1-{frac {1}{mu }}int _{0}^{infty }(1-F(y))^{2},dy={frac {1}{mu }}int _{0}^{infty }F(y)(1-F(y)),dy}

Este último resultado proviene de la integración por partes. (Tenga en cuenta que esta fórmula se puede aplicar cuando hay valores negativos si la integración se toma de menos infinito a más infinito).

El coeficiente de Gini se puede expresar en términos de la función cuantil Q(F) (inversa de la función de distribución acumulada: Q(F(x)) = x)

{displaystyle G={frac {1}{2mu }}int _{0}^{1}int _{0}^{1}|Q(F_{1})-Q(F_{2})|,dF_{1},dF_{2}.}

Dado que el coeficiente de Gini es independiente de la escala, si la función de distribución se puede expresar en la forma f(x,φ,a,b,c...) donde φ es un factor de escala y a,b,c... son parámetros adimensionales, entonces el coeficiente de Gini será una función solo de a,b,c.... Por ejemplo, para la distribución exponencial, que es una función de solo x y un parámetro de escala, el coeficiente de Gini es una constante, igual a 1/2.

Para algunas formas funcionales, el índice Gini se puede calcular explícitamente. Por ejemplo, si Sí. sigue una distribución log-normal con la desviación estándar de troncos igual a $sigma$ , entonces $G=operatorname {erf} left({frac {sigma }{2}}right)$ Donde $operatorname {erf}$ es la función de error (desde ${displaystyle G=2Phi left({frac {sigma }{sqrt {2}}}right)-1}$ , donde $Phi$ es la función de distribución acumulativa de una distribución normal estándar). En el cuadro siguiente, algunos ejemplos de funciones de densidad de probabilidad con apoyo $[0,infty)$ se muestran. La distribución Dirac delta representa el caso en que todos tienen la misma riqueza (o ingresos); no implica variaciones entre los ingresos.

Función de distribución de ingresos	PDF(x)	Coeficiente Gini
Función Dirac delta	$0}" xmlns="http://www.w3.org/1998/Math/MathML">δ δ ()x− − x0),x0■0{displaystyle delta (x-x_{0}),,x_{0} {0}}0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/db5b0aa87688e6070ee35465aee14f4de31b8a10" style="vertical-align: -0.838ex; width:17.478ex; height:2.843ex;"/>$	0
Distribución uniforme	${begin{cases}{frac {1}{b-a}}&aleq xleq b\0&mathrm {otherwise} end{cases}}$	${displaystyle {frac {(b-a)}{3(b+a)}}}$
Distribución exponencial	$0}" xmlns="http://www.w3.org/1998/Math/MathML">λ λ e− − xλ λ ,x■0{displaystyle lambda e^{-xlambda },,,x confianza0}0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/7d446981e5008b4f43bed33306548a985d0f0f61" style="vertical-align: -0.671ex; width:13.247ex; height:3.009ex;"/>$	$1/2$
Distribución lógica	${displaystyle {frac {1}{xsigma {sqrt {2pi }}}}e^{-{frac {1}{2}}left({frac {ln ,(x)-mu }{sigma }}right)^{2}}}$	${displaystyle {textrm {erf}}(sigma /2)=2Phi left({frac {sigma }{sqrt {2}}}right)-1}$
Distribución de los padres	$<math alttext="{displaystyle {begin{cases}{frac {alpha k^{alpha }}{x^{alpha +1}}}&xgeq k\0&x{}α α kα α xα α +1x≥ ≥ k0x.k{displaystyle {begin{cases}{frac {alpha k^{alpha ## {x^{alpha +1}} {}}}}}<img alt="{begin{cases}{frac {alpha k^{alpha }}{x^{alpha +1}}}&xgeq k\0&x$	$<math alttext="{displaystyle {begin{cases}1&0<alpha {}10.α α .112α α - - 1α α \geq \geq 1{fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicroc {1}{2alpha -1}}}} {nMicrosoft Sans Serif} {fnMicrosoft Sans Serif} <img alt="{begin{cases}1&0<alpha$
Distribución Chi	$<math alttext="{displaystyle f(x;k)={begin{cases}{dfrac {x^{k-1}e^{-x^{2}/2}}{2^{k/2-1}Gamma left({frac {k}{2}}right)}},&xgeq 0\0,&xf()x;k)={}xk− − 1e− − x2/22k/2− − 1.. ()k2),x≥ ≥ 00,x.0{displaystyle f(x;k)={begin{cases}{dfrac {x^{k-1}e^{-x^{2}/2}{2^{k/2-1}Gamma left({frac} {k}{2}right)}}}}<img alt="{displaystyle f(x;k)={begin{cases}{dfrac {x^{k-1}e^{-x^{2}/2}}{2^{k/2-1}Gamma left({frac {k}{2}}right)}},&xgeq 0\0,&x$	${displaystyle (-1)^{k}left\|I_{-1}(k,{tfrac {1}{2}})right\|}$
Distribución de Chi-squared	${frac {2^{-k/2}e^{-x/2}x^{k/2-1}}{Gamma (k/2)}}$	${displaystyle {frac {2,Gamma left({frac {1+k}{2}}right)}{k,Gamma (k/2){sqrt {pi }}}}}$
Distribución Gamma	${frac {e^{-x/theta }x^{k-1}theta ^{-k}}{Gamma (k)}}$	${frac {Gamma left({frac {2k+1}{2}}right)}{k,Gamma (k){sqrt {pi }}}}$
Distribución del vestíbulo	${displaystyle {frac {k}{lambda }},left({frac {x}{lambda }}right)^{k-1}e^{-(x/lambda)^{k}}}$	${displaystyle 1-2^{-1/k}}$
Distribución de los beta	${displaystyle {frac {x^{alpha -1}(1-x)^{beta -1}}{B(alphabeta)}}}$	${displaystyle left({frac {2}{alpha }}right){frac {B(alpha +betaalpha +beta)}{B(alphaalpha)B(betabeta)}}}$
Distribución logística de los registros	${displaystyle {frac {(beta /alpha)(x/alpha)^{beta -1}}{left(1+(x/alpha)^{beta }right)^{2}}}}$	$1/beta$

${displaystyle Gamma (,)}$ es la función Gamma
${displaystyle B(,)}$ es la función Beta
${displaystyle I_{k}(,)}$ es la función beta incompleta regularizada

Otros enfoques

A veces no se conoce toda la curva de Lorenz y solo se dan valores en ciertos intervalos. En ese caso, el coeficiente de Gini se puede aproximar usando varias técnicas para interpolar los valores faltantes de la curva de Lorenz. Si (X_k, Y_k) son los puntos conocidos en la curva de Lorenz, con la X_k indexada en orden creciente (X_{k – 1} < X_k), de modo que:

X_k es la proporción acumulada de la variable de población, para k = 0,...n, con X₀ = 0, X_n = 1.
Y_k es la proporción acumulada de la variable de ingreso, para k = 0,...n, con Y₀ = 0, Y_n = 1.
Y_k debe ser indexado en orden no-disminución (Y_k ■ Y_{k – 1})

Si la curva de Lorenz se aproxima en cada intervalo como una línea entre puntos consecutivos, entonces el área B se puede aproximar con trapecios y:

$G_{1}=1-sum _{k=1}^{n}(X_{k}-X_{k-1})(Y_{k}+Y_{k-1})$

es la aproximación resultante para G. Se pueden obtener resultados más precisos usando otros métodos para aproximar el área B, como aproximar la curva de Lorenz con una función cuadrática a través de pares de intervalos o construir una aproximación adecuada a la función de distribución subyacente que coincida con los datos conocidos. Si también se conocen la media de la población y los valores límite para cada intervalo, también se pueden usar a menudo para mejorar la precisión de la aproximación.

El coeficiente de Gini calculado a partir de una muestra es una estadística y se debe informar su error estándar o intervalos de confianza para el coeficiente de Gini de la población. Estos se pueden calcular utilizando técnicas de arranque, matemáticamente complicadas y computacionalmente exigentes incluso en una era de computadoras rápidas. El economista Tomson Ogwang hizo que el proceso fuera más eficiente al establecer un "modelo de regresión truculento" en el que se clasifican las respectivas variables de ingresos de la muestra, asignando el rango 1 al ingreso más bajo. El modelo expresa el rango (variable dependiente) como la suma de una constante A y un término de error normal cuyo la varianza es inversamente proporcional a y_k:

$k=A+ N(0,s^{2}/y_{k})$

Por lo tanto, G puede expresarse como una función de la estimación de mínimos cuadrados ponderados de la constante A y esto puede usarse para acelerar el cálculo de la navaja estimación del error estándar. El economista David Giles argumentó que el error estándar de la estimación de A se puede utilizar para derivar la estimación de G directamente sin utilizar una navaja. Este método solo requiere el uso de regresión de mínimos cuadrados ordinarios después de ordenar los datos de la muestra. Los resultados se comparan favorablemente con las estimaciones del jackknife y la concordancia mejora con el aumento del tamaño de la muestra.

Sin embargo, se ha argumentado que esto depende de las suposiciones del modelo sobre las distribuciones de error y la independencia de los términos de error. Estas suposiciones a menudo no son válidas para conjuntos de datos reales. Todavía hay un debate en curso en torno a este tema.

Guillermina Jasso y Angus Deaton propusieron de forma independiente la siguiente fórmula para el coeficiente de Gini:

${displaystyle G={frac {N+1}{N-1}}-{frac {2}{N(N-1)mu }}(sum _{i=1}^{n}P_{i}X_{i})}$

Donde $mu$ es ingresos medios de la población, P_i es la categoría de ingresos P de persona i, con ingresos X, tal que la persona más rica recibe un rango de 1 y los más pobres un rango de N. Esto da un mayor peso a las personas más pobres en la distribución de ingresos, lo que permite al Gini cumplir con el Principio de Transferencia. Tenga en cuenta que la fórmula Jasso-Deaton reescala el coeficiente para que su valor sea uno si todo el $X_{i}$ son cero excepto uno. Note sin embargo la respuesta de Allison sobre la necesidad de dividir por N2 en su lugar.

FAO explica otra versión de la fórmula.

Índices de desigualdad generalizada

El coeficiente Gini y otros índices de desigualdad estándar reducen a una forma común. La igualdad perfecta —la ausencia de desigualdad— existe cuando y sólo cuando la relación de desigualdad, $r_{j}=x_{j}/{overline {x}}$ , igual 1 para todas las unidades j en alguna población (por ejemplo, hay una igualdad de ingresos perfecta cuando los ingresos de todos $x_{j}$ igual al ingreso medio ${overline {x}}$ Así que $r_{j}=1$ para todos). Las medidas de desigualdad son medidas de las desviaciones medias de las $r_{j}=1$ a partir de 1; cuanto mayor sea la desviación promedio, mayor será la desigualdad. Sobre la base de estas observaciones, los índices de desigualdad tienen esta forma común:

${displaystyle {text{Inequality}}=sum _{j}p_{j},f(r_{j}),}$

donde p_j pondera las unidades por su porcentaje de población, y f(r_j) es una función de la desviación de cada unidad r_j de 1, el punto de igualdad. La idea de este índice de desigualdad generalizada es que los índices de desigualdad difieren porque emplean diferentes funciones de la distancia de las proporciones de desigualdad (la r_j) de 1.

De las distribuciones de ingresos

Derivación de la curva Lorenz y coeficiente Gini para el ingreso mundial en 2011

Los coeficientes de ingresos de Gini se calculan sobre la base de los ingresos de mercado y los ingresos disponibles. El coeficiente de Gini sobre el ingreso de mercado, a veces denominado coeficiente de Gini antes de impuestos, se calcula sobre el ingreso antes de impuestos y transferencias. Mide la desigualdad en el ingreso sin considerar el efecto de los impuestos y el gasto social ya existentes en un país. El coeficiente de Gini sobre el ingreso disponible, a veces denominado coeficiente de Gini después de impuestos, se calcula sobre el ingreso después de impuestos y transferencias. Mide la desigualdad en el ingreso después de considerar el efecto de los impuestos y el gasto social ya establecidos en un país.

Para los países de la OCDE durante el período 2008-2009, el coeficiente de Gini (antes de impuestos y transferencias) para una población total osciló entre 0,34 y 0,53, siendo Corea del Sur el más bajo e Italia el más alto. El coeficiente de Gini (después de impuestos y transferencias) para una población total osciló entre 0,25 y 0,48, siendo Dinamarca el más bajo y México el más alto. Para Estados Unidos, el país con la mayor población entre los países de la OCDE, el índice de Gini antes de impuestos fue de 0,49 y el índice de Gini después de impuestos fue de 0,38 en 2008–2009. El promedio de la OCDE para la población total en los países de la OCDE fue de 0,46 para el índice de Gini de ingresos antes de impuestos y de 0,31 para el índice de Gini de ingresos después de impuestos. Los impuestos y el gasto social que se implementaron en el período 2008-2009 en los países de la OCDE redujeron significativamente la desigualdad de ingresos efectiva y, en general, los países europeos, especialmente los estados de bienestar nórdicos y continentales, logran niveles más bajos de desigualdad de ingresos que otros países. "

Usar el Gini puede ayudar a cuantificar las diferencias en las políticas y filosofías de bienestar y compensación. Sin embargo, debe tenerse en cuenta que el coeficiente de Gini puede ser engañoso cuando se utiliza para hacer comparaciones políticas entre países grandes y pequeños o con políticas de inmigración diferentes (consulte la sección de limitaciones).

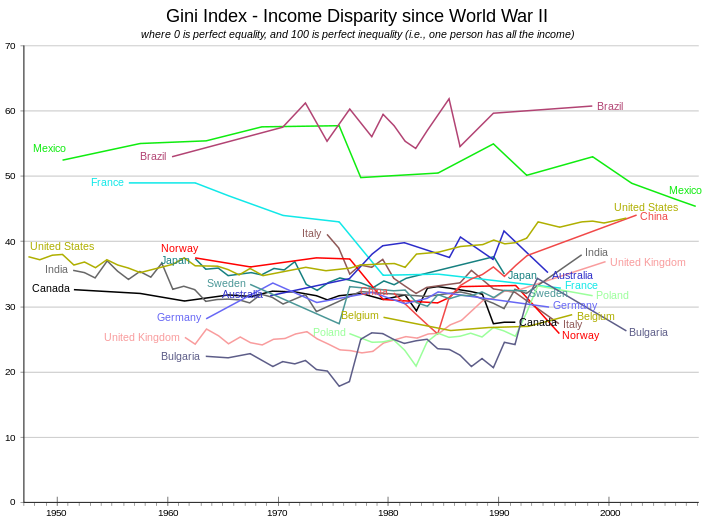
Varias partes han estimado que el coeficiente de Gini para todo el mundo está entre 0,61 y 0,68. El gráfico muestra los valores expresados en porcentaje en su desarrollo histórico para una serie de países.

Índices de Gini de ingresos regionales

Según UNICEF, la región de América Latina y el Caribe tuvo el índice Gini de ingresos netos más alto del mundo con 48,3, sobre una base promedio no ponderada en 2008. Los promedios regionales restantes fueron: África subsahariana (44,2), Asia (40,4), Medio Oriente y África del Norte (39,2), Europa del Este y Asia Central (35,4) y países de ingresos altos (30,9). Usando el mismo método, se afirma que Estados Unidos tiene un índice de Gini de 36, mientras que Sudáfrica tuvo el índice de Gini de ingresos más alto de 67,8.

Índice de Gini de ingresos mundiales desde 1800

Tomando en cuenta la distribución de ingresos de todos los seres humanos, la desigualdad de ingresos en todo el mundo ha ido en constante aumento desde principios del siglo XIX. Hubo un aumento constante en el puntaje de Gini de desigualdad de ingresos global desde 1820 hasta 2002, con un aumento significativo entre 1980 y 2002. Esta tendencia parece haber alcanzado su punto máximo y comenzó una reversión con el rápido crecimiento económico en las economías emergentes, particularmente en las grandes poblaciones de países BRIC.

La siguiente tabla presenta los coeficientes de Gini de ingresos mundiales estimados durante los últimos 200 años, según los cálculos de Milanovic.

Coeficiente Gini de ingresos - Mundo, 1820–2005
Año	Coeficientes Mundiales Gini
1820	0.43
1850	0,53
1870	0,56
1913	0.61
1929	0,622
1950	0,644
1960	0,644
1980	0.66
2002	0.71
2005	0,688

Datos más detallados de fuentes similares muestran un declive continuo desde 1988. Esto se atribuye a que la globalización aumentó los ingresos de miles de millones de personas pobres, principalmente en países como China e India. Los países en desarrollo como Brasil también han mejorado los servicios básicos como la atención médica, la educación y el saneamiento; otros como Chile y México han promulgado políticas fiscales más progresivas.

Coeficiente Gini de ingresos - Mundo, 1988-2013
Año	Coeficientes Mundiales Gini
1988	0.80
1993	0,76
1998	0,74
2003	0.72
2008	0
2013	0.65

De desarrollo social

El coeficiente de Gini se usa ampliamente en campos tan diversos como la sociología, la economía, las ciencias de la salud, la ecología, la ingeniería y la agricultura. Por ejemplo, en ciencias sociales y economía, además de los coeficientes de Gini de ingresos, los académicos han publicado coeficientes de Gini de educación y coeficientes de Gini de oportunidad.

Educación

El índice de Gini de educación estima la desigualdad en educación para una población determinada. Se utiliza para discernir tendencias en el desarrollo social a través del logro educativo a lo largo del tiempo. Un estudio realizado en 85 países por tres economistas del Banco Mundial, Vinod Thomas, Yan Wang y Xibo Fan, estimó que Malí tenía el índice Gini de educación más alto de 0,92 en 1990 (lo que implica una desigualdad muy alta en el nivel educativo de la población), mientras que Estados Unidos tenía el índice Gini de desigualdad educativa más bajo de 0,14. Entre 1960 y 1990, China, India y Corea del Sur tuvieron la caída más rápida en el Índice Gini de desigualdad educativa. También afirman que el índice de Gini de educación para los Estados Unidos aumentó ligeramente durante el período 1980-1990.

Oportunidad

Con un concepto similar al coeficiente de ingreso de Gini, el coeficiente de oportunidad de Gini mide la desigualdad de oportunidades. El concepto se basa en la sugerencia de Amartya Sen de que los coeficientes de desigualdad del desarrollo social deben tener como premisa el proceso de ampliar las opciones de las personas y mejorar sus capacidades, en lugar del proceso de reducir la desigualdad de ingresos. Kovacevic, en una revisión del coeficiente de oportunidad de Gini, explicó que el coeficiente estima qué tan bien una sociedad permite a sus ciudadanos lograr el éxito en la vida donde el éxito se basa en las elecciones, los esfuerzos y los talentos de una persona, no en sus antecedentes definidos. por un conjunto de circunstancias predeterminadas al momento del nacimiento, como sexo, raza, lugar de nacimiento, ingresos de los padres y circunstancias fuera del control de esa persona.

En 2003, Roemer informó que Italia y España exhibieron el mayor índice Gini de desigualdad de oportunidades entre las economías avanzadas.

Movilidad de ingresos

En 1978, Anthony Shorrocks introdujo una medida basada en los coeficientes de Gini de ingresos para estimar la movilidad de ingresos. Esta medida, generalizada por Maasoumi y Zandvakili, ahora se conoce generalmente como índice de Shorrocks, a veces como índice de movilidad de Shorrocks o índice de rigidez de Shorrocks. Intenta estimar si el coeficiente de Gini de desigualdad de ingresos es permanente o temporal y en qué medida un país o región permite la movilidad económica de sus habitantes para que puedan pasar de un cuantil de ingresos (por ejemplo, el 20% inferior) a otro (por ejemplo, medio). 20%) con el tiempo. En otras palabras, el índice de Shorrocks compara la desigualdad de ingresos a corto plazo, como el ingreso anual de los hogares, con la desigualdad de ingresos a largo plazo, como el ingreso total de 5 o 10 años para los mismos hogares.

El índice de Shorrocks se calcula de varias maneras diferentes, siendo un enfoque común la relación de los coeficientes de Gini de ingresos entre el corto y el largo plazo para la misma región o país.

Un estudio de 2010 que utilizó datos de ingresos de seguridad social para los Estados Unidos desde 1937 e índices de Shorrock basados en Gini concluye que la movilidad de ingresos en los Estados Unidos ha tenido una historia complicada, principalmente debido a la afluencia masiva de mujeres a la fuerza laboral estadounidense después de la Segunda Guerra Mundial. Las tendencias de desigualdad de ingresos y movilidad de ingresos han sido diferentes para hombres y mujeres trabajadores entre 1937 y la década de 2000. Cuando los hombres y las mujeres se consideran juntos, las tendencias del índice Shorrocks basado en el coeficiente de Gini implican que la desigualdad de ingresos a largo plazo se ha reducido sustancialmente entre todos los trabajadores, en las últimas décadas para los Estados Unidos. Otros académicos, utilizando solo datos de la década de 1990 u otros períodos cortos, han llegado a conclusiones diferentes. Por ejemplo, Sastre y Ayala concluyen a partir de su estudio de los datos del coeficiente de Gini de ingresos entre 1993 y 1998 para seis economías desarrolladas que Francia tuvo la menor movilidad de ingresos, Italia la más alta y Estados Unidos y Alemania niveles intermedios de movilidad de ingresos durante esos cinco años..

Características

El coeficiente de Gini tiene características que lo hacen útil como medida de dispersión en una población, y de desigualdades en particular.

Limitaciones

El coeficiente de Gini es una medida relativa. El coeficiente de Gini de un país en desarrollo puede aumentar (debido a la creciente desigualdad de ingresos) incluso cuando el número de personas en pobreza absoluta disminuye. Esto se debe a que el coeficiente de Gini mide la riqueza relativa, no absoluta. El cambio en la desigualdad de ingresos, medido por los coeficientes de Gini, puede deberse a cambios estructurales en una sociedad, como el crecimiento de la población (tasas de natalidad más altas, envejecimiento de la población, tasas de divorcio más altas, familias extensas que se dividen en familias nucleares, emigración, inmigración) y movilidad de ingresos. Los coeficientes de Gini son simples, y esta simplicidad puede conducir a descuidos y puede confundir la comparación de diferentes poblaciones; por ejemplo, mientras que tanto Bangladesh (ingreso per cápita de $1693) como los Países Bajos (ingreso per cápita de $42 183) tenían un coeficiente de Gini de ingreso de 0,31 en 2010, la calidad de vida, la oportunidad económica y el ingreso absoluto en estos países son muy diferentes, es decir, los países pueden tener coeficientes de Gini idénticos, pero difieren mucho en riqueza. Las necesidades básicas pueden estar disponibles para todos en una economía desarrollada, mientras que en una economía subdesarrollada con el mismo coeficiente de Gini, las necesidades básicas pueden no estar disponibles para la mayoría o estar disponibles de manera desigual debido a una riqueza absoluta más baja.

Cuadro A. Diferentes distribuciones de ingresos con el mismo índice Gini
Grupo de hogares	País Ingresos anuales ($)	Ingresos anuales del país B ($)
1	20.000	9.000
2	30.000	40.000
3	40.000	48.000
4	50.000	48.000
5	60.000	55.000
Total de ingresos	200.000 dólares	200.000 dólares
País Gini	0.2	0.2

Diferentes distribuciones de ingresos con el mismo coeficiente Gini

Incluso cuando el ingreso total de una población es el mismo, en ciertas situaciones dos países con diferentes distribuciones de ingresos pueden tener el mismo índice de Gini (por ejemplo, casos en los que se cruzan las Curvas de Lorenz de ingresos). La tabla A ilustra una de estas situaciones. Ambos países tienen un coeficiente de Gini de 0,2, pero las distribuciones de ingresos promedio para los grupos de hogares son diferentes. Como otro ejemplo, en una población donde el 50% más bajo de los individuos no tiene ingresos y el otro 50% tiene ingresos iguales, el coeficiente de Gini es 0,5; mientras que para otra población donde el 75% más bajo de las personas tiene el 25% de los ingresos y el 25% superior tiene el 75% de los ingresos, el índice de Gini también es 0,5. Las economías con ingresos y coeficientes de Gini similares pueden tener distribuciones de ingresos muy diferentes. Bellù y Liberati afirman que no siempre es posible clasificar la desigualdad de ingresos entre dos poblaciones en función de sus índices de Gini. De manera similar, el científico social computacional Fabian Stephany ilustra que la desigualdad de ingresos dentro de la población, por ejemplo, en grupos socioeconómicos específicos de la misma edad y educación, tampoco se detecta en los índices de Gini convencionales.

Inequidad de la riqueza extrema, pero coeficiente Gini de bajos ingresos

Un índice Gini no contiene información sobre los ingresos nacionales o personales absolutos. Las poblaciones pueden tener simultáneamente índices Gini de ingresos muy bajos e índices Gini de riqueza muy altos. Al medir la desigualdad de ingresos, el Gini ignora la eficiencia diferencial del uso de los ingresos de los hogares. Al ignorar la riqueza (excepto si contribuye a los ingresos), el Gini puede crear la apariencia de desigualdad cuando las personas comparadas se encuentran en diferentes etapas de su vida. Los países ricos como Suecia pueden mostrar un coeficiente de Gini bajo para el ingreso disponible de 0,31, por lo que parecen iguales, pero tienen un coeficiente de Gini muy alto para la riqueza de 0,79 a 0,86, lo que sugiere una distribución de la riqueza extremadamente desigual en su sociedad. Estos factores no se evalúan en el Gini basado en los ingresos.

Cuadro B. Misma distribución de los ingresos, pero diferente índice Gini
Número de hogares	Ingresos anuales por países ($)	Número combinado de hogares	País A combinado de ingresos anuales ($)
1	20.000	1 2	50.000
2	30.000	1 2	50.000
3	40.000	3 " 4	90.000
4	50.000	3 " 4	90.000
5	60.000	5 " 6	130.000
6	70.000	5 " 6	130.000
7	80.000	7 " 8	170.000
8	90.000	7 " 8	170.000
9	120.000	9 " 10	270,000
10	150.000	9 " 10	270,000
Total de ingresos	710.000		710.000
País Gini	0.303		0.293

Sesgo de muestras pequeñas – regiones poco pobladas más probable que tengan bajo coeficiente Gini

El índice de Gini tiene un sesgo a la baja para poblaciones pequeñas. Los condados, estados o países con poblaciones pequeñas y economías menos diversas tenderán a reportar coeficientes de Gini bajos. Para grandes grupos de población económicamente diversos, se espera un coeficiente mucho mayor que para cada una de sus regiones. Por ejemplo, tomando la economía mundial como un todo y la distribución del ingreso para todos los seres humanos, diferentes estudiosos estiman que el índice de Gini global oscila entre 0,61 y 0,68. Al igual que con otros coeficientes de desigualdad, el coeficiente de Gini está influenciado por la granularidad de las mediciones. Por ejemplo, cinco cuantiles del 20 % (baja granularidad) generalmente generarán un coeficiente de Gini más bajo que veinte cuantiles del 5 % (alta granularidad) para la misma distribución. Philippe Monfort ha demostrado que el uso de granularidad inconsistente o no especificada limita la utilidad de las mediciones del coeficiente de Gini.

La medida del coeficiente de Gini arroja resultados diferentes cuando se aplica a individuos en lugar de a hogares, para la misma economía y las mismas distribuciones de ingresos. Si se utilizan datos del hogar, el valor medido del Gini del ingreso depende de cómo se defina el hogar. La comparación no tiene sentido cuando las diferentes poblaciones no se miden con definiciones consistentes.

Deininger y Squire (1996) muestran que el coeficiente de Gini del ingreso basado en el ingreso individual en lugar del ingreso familiar es diferente. Por ejemplo, para Estados Unidos encontraron que el índice de Gini basado en el ingreso individual era de 0,35, mientras que para Francia era de 0,43. De acuerdo con su método centrado en el individuo, en los 108 países que estudiaron, Sudáfrica tenía el coeficiente de Gini más alto del mundo con 0,62, Malasia tenía el coeficiente de Gini más alto de Asia con 0,5, Brasil el más alto con 0,57 en América Latina. América y la región del Caribe, y Turquía, la más alta con 0,5 en los países de la OCDE.

Table C. Household money income distributions and Gini Index, US
Soporte de ingresos (en dólares ajustados en 2010)	Porcentaje de población 1979	Porcentaje de población 2010
Menos de 15.000 dólares	14,6%	13,7%
$15,000 – $24,999	11,9%	12.0%
$25,000 – $34,999	12.1%	10,9%
$35,000 – $49,999	15,4%	13,9%
$50.000 – $74,999	22,1%	17.7%
$75,000 – $99,999	12.4%	11,4%
$100,000 – $149,999	8.3%	12.1%
$150,000 – $199,999	2.0%	4,5%
200.000 dólares y más	1,2%	3,9%
Total de hogares	80.776.000	118.682.000
Gini de los Estados Unidos sobre la base previa a impuestos	0.404	0.469

El coeficiente Gini no puede discernir los efectos de los cambios estructurales en las poblaciones

Expandiendo la importancia de las medidas de la vida útil, el coeficiente de Gini como una estimación puntual de la igualdad en un momento determinado ignora los cambios en los ingresos a lo largo de la vida. Por lo general, los aumentos en la proporción de miembros jóvenes o mayores de una sociedad generarán cambios aparentes en la igualdad simplemente porque las personas generalmente tienen ingresos y riqueza más bajos cuando son jóvenes que cuando son mayores. Debido a esto, factores como la distribución por edades dentro de una población y la movilidad dentro de las clases de ingresos pueden crear la apariencia de desigualdad cuando no existe, teniendo en cuenta los efectos demográficos. Por lo tanto, una economía determinada puede tener un coeficiente de Gini más alto en cualquier punto de tiempo en comparación con otra, mientras que el coeficiente de Gini calculado sobre individuos' el ingreso de por vida es más bajo que el de la economía aparentemente más igualitaria (en un momento dado). Esencialmente, lo que importa no es solo la desigualdad en un año en particular, sino la composición de la distribución a lo largo del tiempo.

El multimillonario Thomas Kwok afirmó que el coeficiente Gini de ingresos de Hong Kong ha sido alto (0,434 en 2010), en parte debido a cambios estructurales en su población. En las últimas décadas, Hong Kong ha sido testigo de un número creciente de hogares pequeños, hogares de ancianos y ancianos que viven solos. El ingreso combinado ahora se divide en más hogares. Muchas personas mayores viven separadas de sus hijos en Hong Kong. Estos cambios sociales han provocado cambios sustanciales en la distribución del ingreso de los hogares. El coeficiente de Gini de la renta, afirma Kwok, no discierne estos cambios estructurales en su sociedad. La distribución del ingreso monetario de los hogares de Estados Unidos, resumida en el Cuadro C de esta sección, confirma que este problema no se limita solo a Hong Kong. Según la Oficina del Censo de los Estados Unidos, entre 1979 y 2010, la población de los Estados Unidos experimentó cambios estructurales en los hogares en general; los ingresos de todos los tramos de ingresos aumentaron en términos ajustados por inflación, las distribuciones de ingresos de los hogares cambiaron a tramos de ingresos más altos con el tiempo, mientras que el coeficiente de Gini de ingresos aumentó.

Otra limitación del coeficiente de Gini es que no es una medida adecuada de igualitarismo, ya que solo mide la dispersión del ingreso. Por ejemplo, supongamos que dos países igualmente igualitarios siguen políticas de inmigración diferentes. En ese caso, el país que acepte una mayor proporción de migrantes empobrecidos o de bajos ingresos reportará un coeficiente de Gini más alto y, por lo tanto, puede exhibir una mayor desigualdad de ingresos.

La incapacidad para valorar los beneficios y los ingresos de la economía informal afecta a la exactitud del coeficiente de Gini

Algunos países distribuyen beneficios que son difíciles de valorar. Los países que brindan vivienda subsidiada, atención médica, educación u otros servicios similares son difíciles de evaluar objetivamente, ya que depende de la calidad y el alcance del beneficio. En ausencia de un mercado libre, valorar estas transferencias de ingresos como ingresos del hogar es subjetivo. El modelo teórico del coeficiente de Gini se limita a aceptar supuestos subjetivos correctos o incorrectos.

En las economías informales e impulsadas por la subsistencia, las personas pueden tener ingresos significativos en otras formas además del dinero, por ejemplo, a través de la agricultura de subsistencia o el trueque. Estos ingresos tienden a acumularse en el segmento de la población por debajo del umbral de pobreza o muy pobre en los países con economías emergentes y en transición, como los del África subsahariana, América Latina, Asia y Europa del Este. La economía informal representa más de la mitad del empleo mundial y hasta el 90 por ciento del empleo en algunos de los países subsaharianos más pobres con altos coeficientes oficiales de desigualdad de Gini. Schneider et al., en su estudio de 2010 de 162 países, informan que alrededor del 31,2 %, o alrededor de 20 billones de dólares, del PIB mundial es informal. En los países en desarrollo, la economía informal predomina en todos los tramos de ingresos excepto en las poblaciones urbanas más ricas de tramos superiores de ingresos. Incluso en las economías desarrolladas, del 8 % (Estados Unidos) al 27 % (Italia) del PIB de cada nación es informal. El ingreso informal resultante predomina como actividad de sustento para aquellos en los tramos de ingresos más bajos. El valor y la distribución de los ingresos de la economía informal o subterránea es difícil de cuantificar, lo que dificulta las estimaciones de los coeficientes de Gini de ingresos reales. Diferentes suposiciones y cuantificaciones de estos ingresos producirán diferentes coeficientes de Gini.

Gini también tiene algunas limitaciones matemáticas. No es aditivo y no se puede promediar diferentes conjuntos de personas para obtener el coeficiente de Gini de todas las personas en los conjuntos.

Alternativas

Dadas las limitaciones del coeficiente de Gini, se utilizan otros métodos estadísticos en combinación o como una medida alternativa de la dispersión de la población. Por ejemplo, las medidas de entropía se utilizan con frecuencia (por ejemplo, el índice de Atkinson o el índice de Theil y la desviación logarítmica media como casos especiales del índice de entropía generalizada). Estas medidas intentan comparar la distribución de recursos por agentes inteligentes en el mercado con una distribución aleatoria de máxima entropía, que ocurriría si estos agentes actuaran como partículas que no interactúan en un sistema cerrado siguiendo las leyes de la física estadística.

Relación con otras medidas estadísticas

Hay una medida sumaria de la capacidad diagnóstica de un sistema de clasificación binario que también se llama el Coeficiente Gini, que se define como dos veces el área entre la curva de características de funcionamiento del receptor (ROC) y su diagonal. Está relacionado con la medida de rendimiento de AUC (Area Under the ROC Curve) dada por $AUC=(G+1)/2$ y a Mann-Whitney U. Aunque ambos coeficientes Gini se definen como áreas entre ciertas curvas y comparten ciertas propiedades, no hay una relación directa simple entre el coeficiente Gini de dispersión estadística y el coeficiente Gini de un clasificador.

El índice de Gini también está relacionado con el índice de Pietra, los cuales miden la heterogeneidad estadística y se derivan de la curva de Lorenz y la línea diagonal.

En ciertos campos como la ecología, inverso el índice de Simpson $1/lambda$ se utiliza para cuantificar la diversidad, y esto no debe confundirse con el índice Simpson $lambda$ . Estos indicadores están relacionados con Gini. El índice inverso de Simpson aumenta con la diversidad, a diferencia del índice Simpson y el coeficiente Gini, que disminuyen con la diversidad. El índice Simpson está en el rango [0, 1], donde 0 significa máximo y 1 significa mínima diversidad (o heterogeneidad). Puesto que los índices de diversidad suelen aumentar con la heterogeneidad creciente, el índice Simpson se transforma a menudo en Simpson inverso, o utilizando el complemento ${displaystyle 1-lambda }$ , conocido como el Índice Gini-Simpson.

Coeficientes de Gini para sociedades premodernas

En las últimas décadas, los investigadores han intentado estimar los coeficientes de Gini para las sociedades anteriores al siglo XX. En ausencia de encuestas de ingresos de los hogares e impuestos sobre la renta, los académicos se han basado en variables indirectas. Estos incluyen los impuestos sobre el patrimonio en las ciudades-estado europeas medievales, los patrones de propiedad de la tierra en el Egipto romano, la variación del tamaño de las casas en las sociedades desde la antigua Grecia hasta el México azteca, y la herencia y las dotes en la sociedad babilónica. Otros datos no documentan directamente las variaciones en la riqueza o los ingresos, pero se sabe que reflejan la desigualdad, como la relación entre rentas y salarios o entre mano de obra y capital.

Otros usos

Aunque el coeficiente de Gini es más popular en economía, en teoría puede aplicarse en cualquier campo de la ciencia que estudie una distribución. Por ejemplo, en ecología, el coeficiente de Gini se ha utilizado como una medida de la biodiversidad, donde la proporción acumulada de especies se representa frente a la proporción acumulada de individuos. En salud, se ha utilizado como medida de la desigualdad de la calidad de vida relacionada con la salud en una población. En educación, se ha utilizado como medida de la desigualdad de las universidades. En química se ha utilizado para expresar la selectividad de los inhibidores de la proteína quinasa frente a un panel de quinasas. En ingeniería, se ha utilizado para evaluar la equidad lograda por los enrutadores de Internet en la programación de transmisiones de paquetes de diferentes flujos de tráfico.

El coeficiente de Gini se utiliza a veces para medir el poder discriminatorio de los sistemas de calificación en la gestión del riesgo crediticio.

Un estudio de 2005 accedió a los datos del censo de EE. UU. para medir la propiedad de computadoras en el hogar y utilizó el coeficiente de Gini para medir las desigualdades entre los blancos y los afroamericanos. Los resultados indicaron que, aunque disminuyó en general, la desigualdad en la posesión de computadoras en el hogar fue sustancialmente menor entre los hogares blancos.

Un estudio revisado por pares de 2016 titulado Empleando el coeficiente de Gini para medir la desigualdad de participación en redes sociales de salud digital centradas en el tratamiento ilustró que el coeficiente de Gini fue útil y preciso para medir los cambios en la desigualdad, sin embargo, como una métrica independiente no pudo incorporar tamaño total de la red.

La potencia discriminatoria se refiere a la capacidad de un modelo de riesgo de crédito para diferenciar entre clientes predeterminados y no predeterminados. La fórmula $G_{1}$ , en la sección de cálculo anterior, puede utilizarse para el modelo final y a nivel de los factores modelo individuales para cuantificar el poder discriminatorio de los factores individuales. Está relacionado con la relación de exactitud de los modelos de evaluación de la población.

El coeficiente de Gini también se ha aplicado para analizar la desigualdad en las aplicaciones de citas.

Kaminskiy y Krivtsov ampliaron el concepto del coeficiente de Gini de la economía a la teoría de la confiabilidad y propusieron un coeficiente de tipo Gini que ayuda a evaluar el grado de envejecimiento de los sistemas no reparables o el envejecimiento y rejuvenecimiento de los sistemas reparables. El coeficiente se define entre -1 y 1 y se puede utilizar tanto en distribuciones de vida empíricas como paramétricas. Toma valores negativos para la clase de distribuciones de tasa de falla decreciente y procesos puntuales con tasa de intensidad de falla decreciente y es positivo para las distribuciones de tasa de falla creciente y procesos puntuales con tasa de intensidad de falla creciente. El valor de cero corresponde a la distribución de vida exponencial o al Proceso Homogéneo de Poisson.

Contenido relacionado

El ingreso per capita
Ingreso per cápita o ingreso total mide el ingreso promedio obtenido por persona en un área determinada en un año específico. Se calcula dividiendo los...
Economía del Perú
La economía del Perú es una economía de mercado social emergente caracterizada por un alto nivel de comercio exterior y una economía de ingresos medios...
Sociedades Europaea
A societas Europaea es una empresa pública registrada de acuerdo con la ley de sociedades de la Unión Europea introducida en 2004 con el Reglamento del...
Más resultados...