Coeficiente de Seebeck

El coeficiente de Seebeck (también conocido como potencia térmica, potencia termoeléctrica y sensibilidad termoeléctrica) de un material es una medida de la magnitud de un voltaje termoeléctrico inducido en respuesta a una diferencia de temperatura a través de ese material, inducida por el efecto Seebeck. La unidad SI del coeficiente de Seebeck es voltios por kelvin (V/K), aunque más a menudo se expresa en microvoltios por kelvin (μV/K).

El uso de materiales con un alto coeficiente de Seebeck es uno de los muchos factores importantes para el comportamiento eficiente de los generadores termoeléctricos y los refrigeradores termoeléctricos. Puede encontrar más información sobre materiales termoeléctricos de alto rendimiento en el artículo Materiales termoeléctricos. En los termopares, el efecto Seebeck se utiliza para medir temperaturas y, para mayor precisión, es deseable utilizar materiales con un coeficiente de Seebeck que sea estable en el tiempo.

Físicamente, la magnitud y el signo del coeficiente de Seebeck pueden entenderse aproximadamente como dados por la entropía por unidad de carga transportada por las corrientes eléctricas en el material. Puede ser positivo o negativo. En conductores que pueden entenderse en términos de portadores de carga casi libres y que se mueven independientemente, el coeficiente de Seebeck es negativo para los portadores con carga negativa (como los electrones) y positivo para los portadores con carga positiva (como los huecos de los electrones).

Definición

Una forma de definir el coeficiente de Seebeck es el voltaje que se genera cuando se aplica un pequeño gradiente de temperatura a un material y cuando el material ha llegado a un estado estable donde la densidad de corriente es cero en todas partes. Si la diferencia de temperatura ΔT entre los dos extremos de un material es pequeña, entonces el coeficiente de Seebeck de un material se define como:

${displaystyle S=-{ Delta V over Delta T}$

donde ΔV es la tensión termoeléctrica vista en los terminales. (Consulte a continuación más información sobre los signos de ΔV y ΔT).

Tenga en cuenta que el cambio de voltaje expresado por el efecto Seebeck no se puede medir directamente, ya que el voltaje medido (conectando un voltímetro) contiene una contribución de voltaje adicional, debido al gradiente de temperatura y al efecto Seebeck en los cables de medición. El voltaje del voltímetro siempre depende de los coeficientes de Seebeck relativos entre los diversos materiales involucrados.

De manera más general y técnica, el coeficiente de Seebeck se define en términos de la porción de corriente eléctrica impulsada por gradientes de temperatura, como en la ecuación diferencial vectorial

${displaystyle mathbf {J} =-sigma {boldsymbol {nabla} V-sigma S{boldsymbol {nabla }T}$

Donde ${displaystyle scriptstyle mathbf {J}$ es la densidad actual, ${displaystyle scriptstyle sigma }$ es la conductividad eléctrica, ${displaystyle scriptstyle {boldsymbol {nabla}V}$ es el gradiente de tensión, y ${displaystyle scriptstyle {boldsymbol {nabla }T}$ es el gradiente de temperatura. El caso especial de estado cero corriente y estable descrito anteriormente ha ${displaystyle scriptstyle mathbf {J} =0}$, lo que implica que los dos términos de conductividad eléctrica han cancelado ${displaystyle {boldsymbol {nabla }V=-S{boldsymbol {nabla} T.$

Convención

El signo se hace explícito en la siguiente expresión:

${displaystyle S=-{frac {fnh}-V_{rm} {} {fn} {fnMicrosoft}} {fnMicrosoft}} {fnMicrosoft}} {fn}}} {fn}}} {fn}}}} {fn}}} {fn}}}} {f}} {f}}}}}}} {f}}}}}}}}} {\\f}}}}}}}}}}}} {\\\\\\f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ {}-T_{rm} {}}}$

Así, si S es positivo, el extremo con mayor temperatura tiene el menor voltaje, y viceversa. El gradiente de voltaje en el material apuntará contra el gradiente de temperatura.

El efecto Seebeck está generalmente dominado por la contribución de la difusión de los portadores de carga (ver más abajo), que tiende a empujar a los portadores de carga hacia el lado frío del material hasta que se haya acumulado un voltaje de compensación. Como resultado, en los semiconductores de tipo p (que sólo tienen cargas móviles positivas, huecos de electrones), S es positivo. Del mismo modo, en los semiconductores de tipo n (que sólo tienen cargas móviles negativas, electrones), S es negativo. Sin embargo, en la mayoría de los conductores, los portadores de carga presentan un comportamiento tanto hueco como electrónico y el signo de S suele depender de cuál de ellos predomina.

Relación con otros coeficientes termoeléctricos

Según la segunda relación Thomson (que mantiene para todos los materiales no magnéticos en ausencia de un campo magnético aplicado externamente), el coeficiente Seebeck está relacionado con el coeficiente Peltier ${displaystyle scriptstyle Pi }$ por la relación exacta

${displaystyle S={frac {f}} {f}}}$

Donde ${displaystyle T}$ es la temperatura termodinámica.

Según la primera relación Thomson y bajo las mismas suposiciones sobre el magnetismo, el coeficiente Seebeck está relacionado con el coeficiente Thomson ${displaystyle scriptstyle {mathcal {K}}$ por

${displaystyle S=int {frac {fnMitcal {K} {T},dT}$

La constante integración es tal que ${displaystyle scriptstyle S=0}$ en absoluto cero, como exige el teorema de Nernst.

Medición

Coeficiente de Seebeck relativo

En la práctica, el coeficiente absoluto de Seebeck es difícil de medir directamente, ya que la salida de voltaje de un circuito termoeléctrico, medida con un voltímetro, sólo depende de las diferencias de los coeficientes de Seebeck. Esto se debe a que se deben colocar electrodos conectados a un voltímetro sobre el material para medir el voltaje termoeléctrico. Entonces, el gradiente de temperatura también suele inducir una tensión termoeléctrica a través de una pata de los electrodos de medición. Por lo tanto, el coeficiente de Seebeck medido es una contribución del coeficiente de Seebeck del material de interés y del material de los electrodos de medición. Esta disposición de dos materiales suele denominarse termopar.

El coeficiente de Seebeck medido es entonces una contribución de ambos y se puede escribir como:

${displaystyle S_{AB}=S_{B}-S_{A}={ Delta V_{B} over Delta T}-{Delta V_{A} over Delta T}$

Coeficiente absoluto de Seebeck

Aunque sólo los coeficientes de Seebeck relativos son importantes para voltajes medidos externamente, el coeficiente de Seebeck absoluto puede ser importante para otros efectos en los que el voltaje se mide indirectamente. Por lo tanto, la determinación del coeficiente absoluto de Seebeck requiere técnicas más complicadas y es más difícil, pero dichas mediciones se han realizado en materiales estándar. Estas mediciones sólo debían realizarse una vez para siempre y para todos los materiales; para cualquier otro material, el coeficiente de Seebeck absoluto se puede obtener realizando una medición del coeficiente de Seebeck relativo frente a un material estándar.

Una medición del coeficiente de Thomson ${displaystyle {fnMithcal}}$, que expresa la fuerza del efecto Thomson, se puede utilizar para producir el coeficiente absoluto Seebeck a través de la relación: ${displaystyle S(T)=int ¿Por qué?$, siempre que ${displaystyle {fnMithcal}}$ se mide hasta cero absoluto. La razón por la que funciona es que ${displaystyle S(T)}$ se espera que disminuya a cero, ya que la temperatura se produce a cero, una consecuencia del teorema de Nernst. Tal medida basada en la integración de ${displaystyle {fnMithcal}/T}$ fue publicado en 1932, aunque dependía de la interpolación del coeficiente de Thomson en ciertas regiones de temperatura.

Los superconductores tienen un coeficiente de Seebeck cero, como se menciona a continuación. Al hacer que uno de los cables de un termopar sea superconductor, es posible obtener una medición directa del coeficiente Seebeck absoluto del otro cable, ya que él solo determina el voltaje medido de todo el termopar. Una publicación de 1958 utilizó esta técnica para medir el coeficiente absoluto de Seebeck del plomo entre 7,2 K y 18 K, llenando así un vacío importante en el experimento anterior de 1932 mencionado anteriormente.

La combinación de la técnica del termopar superconductor hasta 18 K, con la técnica de integración del coeficiente de Thomson por encima de 18 K, permitió determinar el coeficiente absoluto de Seebeck del plomo hasta temperatura ambiente. Por proxy, estas mediciones llevaron a la determinación de coeficientes absolutos de Seebeck para todos los materiales, incluso hasta temperaturas más altas, mediante una combinación de integraciones de coeficientes de Thomson y circuitos de termopares.

La dificultad de estas mediciones y la rareza de reproducir experimentos confieren cierto grado de incertidumbre a la escala termoeléctrica absoluta así obtenida. En particular, las mediciones de 1932 pueden haber medido incorrectamente el coeficiente de Thomson en el rango de 20 K a 50 K. Dado que casi todas las publicaciones posteriores se basaron en esas mediciones, esto significaría que todos los valores comúnmente utilizados del coeficiente absoluto de Seebeck (incluidos los que se muestran en las figuras) son demasiado bajos en aproximadamente 0,3 μV/K, para todas las temperaturas superiores a 50 K.

Coeficientes de Seebeck para algunos materiales comunes

En la siguiente tabla se muestran los coeficientes de Seebeck a temperatura ambiente para algunos materiales comunes no exóticos, medidos en relación con el platino. El coeficiente de Seebeck del platino en sí es aproximadamente −5 μV/K a temperatura ambiente, por lo que los valores enumerados a continuación deben compensarse en consecuencia. Por ejemplo, los coeficientes de Seebeck de Cu, Ag, Au son 1,5 μV/K y los de Al −1,5 μV/K. El coeficiente de Seebeck de los semiconductores depende en gran medida del dopaje, con valores generalmente positivos para p materiales dopados y valores negativos para n dopaje.

Factores físicos que determinan el coeficiente de Seebeck

La temperatura, la estructura cristalina y las impurezas de un material influyen en el valor de los coeficientes termoeléctricos. El efecto Seebeck se puede atribuir a dos cosas: la difusión del portador de carga y el arrastre de fonones.

Difusión del portador de carga

En un nivel fundamental, una diferencia de voltaje aplicada se refiere a una diferencia en el potencial químico termodinámico de los portadores de carga, y la dirección de la corriente bajo una diferencia de voltaje está determinada por el proceso termodinámico universal en el que (dadas temperaturas iguales) las partículas fluir desde un potencial químico alto a un potencial químico bajo. En otras palabras, la dirección de la corriente en la ley de Ohm se determina mediante la flecha termodinámica del tiempo (la diferencia de potencial químico podría aprovecharse para producir trabajo, pero en cambio se disipa en forma de calor, lo que aumenta la entropía). Por otro lado, para el efecto Seebeck ni siquiera el signo de la corriente se puede predecir a partir de la termodinámica, por lo que para entender el origen del coeficiente de Seebeck es necesario entender la física microscópica.

Los portadores de carga (como electrones excitados térmicamente) constantemente difusan alrededor de un material conductivo. Debido a las fluctuaciones térmicas, algunos de estos transportistas de carga viajan con una energía más alta que la media, y algunos con una energía más baja. Cuando no se aplican diferencias de tensión o de temperatura, la difusión del transportista se equilibra perfectamente y por lo tanto en promedio no se ve ninguna corriente: ${displaystyle scriptstyle mathbf {J} =0}$. Una corriente neta se puede generar aplicando una diferencia de tensión (ley de Ohm), o aplicando una diferencia de temperatura (efecto Seebeck). Para entender el origen microscópico del efecto termoeléctrico, es útil describir primero el mecanismo microscópico de la conducta eléctrica normal de Ohm para describir lo que determina el ${displaystyle scriptstyle sigma }$ dentro ${displaystyle scriptstyle mathbf {J} =-sigma {boldsymbol {nabla}V}$. Microscópicamente, lo que está sucediendo en la ley de Ohm es que los niveles de energía más altos tienen una mayor concentración de portadores por estado, en el lado con mayor potencial químico. Para cada intervalo de energía, los transportistas tienden a difundir y diseminar en el área del dispositivo donde hay menos portadores por estado de esa energía. A medida que se mueven, sin embargo, ocasionalmente se dispersan disitivamente, que re-randomiza su energía según la temperatura local y el potencial químico. Esta disipación vacia los portadores de estos estados de energía superior, permitiendo más difundir. La combinación de difusión y disipación favorece una deriva general de los transportistas de carga hacia el lado del material donde tienen un potencial químico inferior.

Para el efecto termoeléctrico, ahora, considere el caso de voltaje uniforme (potencia química uniforme) con un gradiente de temperatura. En este caso, en el lado más caliente del material hay más variación en las energías de los portadores de carga, en comparación con el lado más frío. Esto significa que los altos niveles de energía tienen una ocupación de portador más alta por estado en el lado más caliente, pero también el lado más caliente tiene un inferior ocupación por estado a niveles de energía más bajos. Como antes, los portadores de alta energía difusan del extremo caliente, y producen entropía al derivar hacia el extremo frío del dispositivo. Sin embargo, hay un proceso de competencia: al mismo tiempo los portadores de baja energía se arrastran hacia el extremo caliente del dispositivo. Aunque estos procesos generan entropía, trabajan el uno contra el otro en términos de carga actual, y por lo tanto una corriente neta sólo ocurre si una de estas derivas es más fuerte que la otra. La corriente neta es dada por ${displaystyle scriptstyle mathbf {J} =-sigma S{boldsymbol {nabla }T}$, donde (como se muestra a continuación) el coeficiente termoeléctrico ${displaystyle scriptstyle sigma S.$ depende literalmente de cómo los portadores conductivos de alta energía son, en comparación con los portadores de baja energía. La distinción puede deberse a una diferencia en la tasa de dispersión, una diferencia en las velocidades, una diferencia en la densidad de los estados, o una combinación de estos efectos.

Fórmula de Mott

Los procesos descritos anteriormente se aplican en materiales donde cada portador de carga ve un entorno esencialmente estático, de modo que su movimiento puede describirse independientemente de otros portadores e independiente de otras dinámicas (como los fonones). En particular, en materiales electrónicos con interacciones débiles electrón-electrón, interacciones débiles electrón-fonón, etc., se puede demostrar en general que la conductancia de respuesta lineal es

${displaystyle sigma =int c(E){Bigg (}-{frac {df(E)}{dE}{Bigg)},dE,}$

y el coeficiente termoeléctrico de respuesta lineal es

${displaystyle sigma S={frac {k_{rm {B}}{-e}int {fnMic {E-mu ¿Qué?$

Donde ${displaystyle scriptstyle c(E)}$ es la conductividad dependiente de la energía, y ${displaystyle scriptstyle f(E)}$ es la función de distribución Fermi-Dirac. Estas ecuaciones se conocen como las relaciones Mott, de Sir Nevill Francis Mott. El derivado

${displaystyle -{frac {f}{dE}={frac {1}{4k_{rm [B}T}operatorname {sech} ^{2}left({frac] {E-mu - Sí.$

es una función pico alrededor del potencial químico (nivel férmico) ${displaystyle mu }$ con un ancho de aproximadamente ${displaystyle 3.5k_{rm {B}T}$. La conductividad que depende de la energía (una cantidad que en realidad no puede medirse directamente) sólo mide ${displaystyle sigma }$) se calcula como ${displaystyle c(E)=e^{2}D(E)nu (E)}$ Donde ${displaystyle D(E)}$ es la constante de difusión de electrones y ${displaystyle nu (E)}$ es la densidad electrónica de estados (en general, ambos son funciones de energía).

En materiales con interacciones fuertes, ninguna de las ecuaciones anteriores se puede utilizar ya que no es posible considerar cada portador de carga como una entidad separada. La ley de Wiedemann-Franz también se puede derivar exactamente utilizando la imagen del electrón que no interactúa, por lo que en materiales donde falla la ley de Wiedemann-Franz (como los superconductores), las relaciones de Mott generalmente también tienden a fallar.

Las fórmulas anteriores se pueden simplificar en un par de casos limitantes importantes:

Fórmula de Mott en metales

En semimetales y metales, donde el transporte sólo ocurre cerca del nivel de Fermi y ${displaystyle scriptstyle c(E)}$ cambia lentamente en el rango ${displaystyle Eapprox mu pm k_{rm {B}T}$, uno puede realizar una expansión de Sommerfeld ${displaystyle scriptstyle c(E)=c(mu)+c'(E-mu)+O[(E-mu)^{2}]$, que conduce a

${displaystyle S_{rm {fnh}={frac {fnfnh} ^{2}k_{rm {B}}{2}T}{-3e}{frac {c'(mu)} {c(mu)}}+O[(k_{rm {rm {B}}T)}],quad sigma _{rm {rm}=c(mu)+O[(k_{rm {b}T}}} {c}}}}}}} {c}} {c}}}}}}}}} {c}}}}}}}} {c}}}} {c}}}}}}}}} {c}}}}}}}}}}}} {c}}}}}}} {c} {c}}}} {c}}}}}}}}}} {ccc}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {c}$

Esta expresión a veces se denomina "la fórmula de Mott", sin embargo, es mucho menos general que la fórmula original de Mott expresada anteriormente.

En el modelo de electrones gratis con dispersión, el valor de ${displaystyle scriptstyle c'(mu)/c(mu)}$ es de orden ${displaystyle scriptstyle 1/(k_{rm {B}T_{rm {F}}}$, donde ${displaystyle T_{rm {F}}$ es la temperatura Fermi, y por lo tanto un valor típico del coeficiente Seebeck en el gas Fermi es ${displaystyle scriptstyle S_{rm {Fermi~gas}approx {tfrac {pi} ^{2}k_{rm {B}{-3e}T/T_{rm} {F}}$ (el prefactor varía un poco dependiendo de detalles como la dimensionalidad y la dispersión). En metales altamente conductivos las temperaturas Fermi son típicamente alrededor de 10⁴ – 10⁵ K, y por lo tanto es comprensible por qué sus coeficientes absolutos Seebeck son sólo de orden 1 – 10 μV/K a temperatura ambiente. Tenga en cuenta que mientras que el modelo de electrones libres predice un coeficiente negativo Seebeck, los metales reales tienen estructuras de banda complicadas y pueden exhibir coeficientes Seebeck positivos (ejemplos: Cu, Ag, Au).

La fracción ${displaystyle scriptstyle c'(mu)/c(mu)}$ en semimetales a veces se calcula a partir del derivado medido de ${displaystyle scriptstyle sigma _{rm { metal}}$ con respecto a algún cambio de energía inducido por el efecto de campo. Esto no es necesariamente correcto y la estimación ${displaystyle scriptstyle c'(mu)/c(mu)}$ puede ser incorrecto (por un factor de dos o más), ya que el potencial de trastorno depende de la detección que también cambia con efecto de campo.

Fórmula de Mott en semiconductores

En semiconductores a bajos niveles de dopaje, el transporte sólo se produce lejos del nivel Fermi. A bajo dopaje en la banda de conducción (donde ${displaystyle scriptstyle E_{rm}-mu gg k_{rm} {B}T}$, donde ${displaystyle scriptstyle E_{rm {C}}$ es la energía mínima del borde de la banda de conducción), uno tiene ${displaystyle scriptstyle -{frac {df(E)}{dE}approx {tfrac {1}{k_{rm {B}T}e^{-(E-mu)/(k_{rm {B}T)}$. Aproximando la función de conductividad de los niveles de banda de conducción como ${displaystyle scriptstyle c(E)=A_{rm {C}(E-E_{rm {C}) {C}}$ para algunas constantes ${displaystyle scriptstyle A_{rm {C}}$ y ${displaystyle scriptstyle a_{rm {C}}$,

${displaystyle S_{rm {C}={frac} {k_{rm {B} {fn} {fn}} {fn}}} {fn}}} {fn}}} {f}}}} {fn}}}} {fn}}}} {fn}}}}} {c}}}}} {f}}}}}}}} {f}}}}}}}}} { Grande. {E_{rm {C}-mu} }{k_{rm {B}T}+a_{rm} {C}+1{Big]}quad sigma _{rm {C}=A_{rm} {C}(k_{rm} {B}T)^{a_{rm {C}}e^{-{frac} {E_{fn} {C}-mu }{k_{rm Gamma (a_{rm {C}+1).}$

mientras que en la banda de valence cuando ${displaystyle scriptstyle mu -E_{rm {V}gg kT}$ y ${displaystyle scriptstyle c(E)=A_{rm {fnMicrosoft Sans Serif} {}}$,

${displaystyle S_{rm {V}={frac} {k}{e}{ Grande. -E_{rm {fn} {fn} {fn}} {fn}} {fn}} {fn}} {fn}} {fn}}} {fn}}} {fn}}}} {fn}}} {cH} {f}}}}} {cHFF}}}} {cH}}}}} {cccH}}}}}} {ccccH}}}} {cccccH} {cccccccccc}}}}}}} {ccccccccc} {cHFF}}}}} {ccccccHFF}}}}}}} {cHFF} {cHFF} {ccHFF} {cHFF} {cccc {B}T}+a_{rm} {V}+1{Big}}quad sigma _{rm {V}=A_{rm} {V}(k_{rm} {B}T)^{a_{rm {}e^{-{frac} # -E_{rm {fn} {fn} {fn}} {fn}} {fn}} {fn}} {fn}} {fn}}} {fn}}} {fn}}}} {fn}}} {cH} {f}}}}} {cHFF}}}} {cH}}}}} {cccH}}}}}} {ccccH}}}} {cccccH} {cccccccccc}}}}}}} {ccccccccc} {cHFF}}}}} {ccccccHFF}}}}}}} {cHFF} {cHFF} {ccHFF} {cHFF} {cccc Gamma (a_{rm {}+1).}$

Los valores de ${displaystyle scriptstyle a_{rm {C}}$ y ${displaystyle scriptstyle a_{rm {V}}$ depende de los detalles materiales; en semiconductor a granel estas constantes oscilan entre 1 y 3, los extremos correspondientes a la dispersión de celo acústico y dispersión de la inmpuridad ionizada.

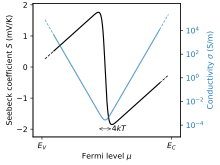
En los semiconductores extrínsecos (dopados), la banda de conducción o la de valencia dominarán el transporte, por lo que uno de los números anteriores dará los valores medidos. Sin embargo, en general, el semiconductor también puede ser intrínseco, en cuyo caso las bandas conducen en paralelo, por lo que los valores medidos serán

${displaystyle S_{rm {rm}={frac} {sigma _{rm {C}S_{rm} {C}+sigma _{rm} {V}S_{rm} {V}}{sigma _{rm} {C}+sigma _{rm {V}}}quad sigma _{rm} {semi}=sigma {C}+sigma _{rm} {V}}$

Esto resulta en un comportamiento cruzado, como se muestra en la figura. El coeficiente Seebeck más alto se obtiene cuando el semiconductor es ligeramente dopado, sin embargo un alto coeficiente Seebeck no es necesariamente útil por sí mismo. Para los dispositivos termoeléctricos (coolers, generadores) es más importante maximizar el factor de potencia termoeléctrica ${displaystyle scriptstyle sigma S^{2}$, o la figura termoeléctrica del mérito, y el óptimo generalmente ocurre en altos niveles de dopaje.

Arrastre de fonones

Los fonones no siempre están en equilibrio térmico local; se mueven contra el gradiente térmico. Pierden impulso al interactuar con electrones (u otros portadores) y con imperfecciones del cristal. Si la interacción fonón-electrón es predominante, los fonones tenderán a empujar los electrones hacia un extremo del material, perdiendo así impulso y contribuyendo al campo termoeléctrico. Esta contribución es más importante en la región de temperatura donde predomina la dispersión de fonones y electrones. Esto sucede por

${displaystyle Tapprox {1 over 5}theta ¿Qué?$

Donde ${displaystyle scriptstyle theta _{rm {}}$ es la temperatura de Debye. A temperaturas más bajas hay menos fonones disponibles para el arrastre, y a temperaturas más altas tienden a perder el impulso en la dispersión fonón-fón en lugar de dispersión fonón-electrón. A temperaturas inferiores, los límites materiales también juegan un papel cada vez mayor ya que los fonones pueden viajar distancias significativas. Prácticamente hablando, la arrastre fonón es un efecto importante en semiconductores cerca de la temperatura ambiente (aunque muy por encima) ${displaystyle scriptstyle theta _{rm {D}/5}$), que es comparable en magnitud con el efecto de la diffusión de portador descrito en la sección anterior.

Esta región de la función termopotencia versus temperatura es altamente variable bajo un campo magnético.

Relación con la entropía

El coeficiente de Seebeck de un material corresponde termodinámicamente a la cantidad de entropía "arrastrada" por el flujo de carga dentro de un material; en cierto sentido, es la entropía por unidad de carga en el material.