Clasificador lineal

En el campo del aprendizaje automático, el objetivo de la clasificación estadística es utilizar las características de un objeto para identificar a qué clase (o grupo) pertenece. Un clasificador lineal logra esto tomando una decisión de clasificación basada en el valor de una combinación lineal de las características. Las características de un objeto también se conocen como valores de características y, por lo general, se presentan a la máquina en un vector denominado vector de características. Dichos clasificadores funcionan bien para problemas prácticos como la clasificación de documentos y, de manera más general, para problemas con muchas variables (características), alcanzando niveles de precisión comparables a los clasificadores no lineales y tomando menos tiempo para entrenar y usar.

Definición

En este caso, los puntos sólidos y vacíos pueden clasificarse correctamente por cualquier número de clasificadores lineales. H1 (azul) los clasifica correctamente, al igual que H2 (rojo). H2 podría ser considerado "mejor" en el sentido de que también es más lejos de ambos grupos. H3 (verde) no clasifica correctamente los puntos.

Si la característica de entrada vector al clasificador es un vector real x→ → {displaystyle {vec {x}}, entonces la puntuación de salida es

Sí.=f()w→ → ⋅ ⋅ x→ → )=f().. jwjxj),{displaystyle y=f({vec}cdot {vec})=fleft(sum _{j}w_{j}x_{j}right),}

Donde w→ → {displaystyle {vec}} es un verdadero vector de pesos y f es una función que convierte el producto de puntos de los dos vectores en la salida deseada. (En otras palabras, w→ → {displaystyle {vec}} es un mapeo funcional de una forma o lineal x→ → {displaystyle {vec {x}} sobre R.) El vector de peso w→ → {displaystyle {vec}} se aprende de un conjunto de muestras de entrenamiento etiquetadas. A menudo f es un función umbral, que mapea todos los valores de w→ → ⋅ ⋅ x→ → {displaystyle {vec}cdot {vec}} por encima de un determinado umbral a la primera clase y todos los demás valores a la segunda clase; por ejemplo,

theta\0&{text{otherwise}}end{cases}}}" xmlns="http://www.w3.org/1998/Math/MathML">f()x)={}1siwT⋅ ⋅ x■Silencio Silencio ,0de otra manera{displaystyle f(mathbf {x})={begin{cases}1 {text{if} mathbf {w}cdot mathbf {x} }theta limit{text{otherwise}}end{cases}}theta\0&{text{otherwise}}end{cases}}}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/a40282bc09a38e14cfaabe35ffe2ee2bee6c54f6" style="vertical-align: -2.505ex; width:27.343ex; height:6.176ex;"/>

El superscripto T indica la transposición y Silencio Silencio {displaystyle theta } es un umbral de escalar. Un complejo f podría dar la probabilidad de que un artículo pertenece a una determinada clase.

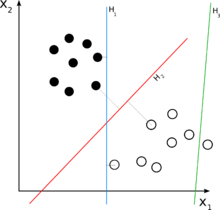
Para un problema de clasificación de dos clases, uno puede visualizar la operación de un clasificador lineal como dividir un espacio de entrada de alta dimensión con un hiperplano: todos los puntos en un lado del hiperplano se clasifican como "sí", mientras que los demás se clasifican como "no".

A menudo se utiliza un clasificador lineal en situaciones donde la velocidad de clasificación es un problema, ya que a menudo es el clasificatorio más rápido, especialmente cuando x→ → {displaystyle {vec {x}} es escasa. Además, los clasificadores lineales a menudo funcionan muy bien cuando el número de dimensiones en x→ → {displaystyle {vec {x}} es grande, como en la clasificación de documentos, donde cada elemento en x→ → {displaystyle {vec {x}} suele ser el número de ocurrencias de una palabra en un documento (véase la matriz a plazo de documento). En tales casos, el clasificador debe ser bien regularizado.

Modelos generativos vs modelos discriminativos

Hay dos amplias clases de métodos para determinar los parámetros de un clasificador lineal w→ → {displaystyle {vec}}. Pueden ser modelos generativos y discriminativos. Métodos de distribución de probabilidad articular modelo anterior, mientras que los métodos de este último modelo de funciones de densidad condicional P()classSilenciox→ → ){displaystyle P({rmcl}tuvo {vec}}}. Ejemplos de tales algoritmos incluyen:

• Análisis lineal de descriminantes (LDA) - asume modelos Gaussian de densidad condicional
• Clasificador Naive Bayes con modelos de eventos multinomiales o multivariables Bernoulli.

El segundo conjunto de métodos incluye modelos discriminativos, que intentan maximizar la calidad de la salida en un conjunto de entrenamiento. Los términos adicionales en la función de costo de capacitación pueden realizar fácilmente la regularización del modelo final. Los ejemplos de entrenamiento discriminativo de clasificadores lineales incluyen:

• Regresión logística - estimación de probabilidad máxima de w→ → {displaystyle {vec}} suponiendo que el conjunto de entrenamiento observado fue generado por un modelo binomio que depende de la salida del clasificador.
• Perceptron: un algoritmo que intenta corregir todos los errores encontrados en el conjunto de entrenamiento
• Análisis de Discriminantes Lineales de Fisher: un algoritmo (diferente que "LDA") que maximiza la relación entre la dispersión de clase a la dispersión dentro de clase, sin otras suposiciones. Es en esencia un método de reducción de la dimensionalidad para la clasificación binaria.
• Soporte de máquina vectorial: un algoritmo que maximiza el margen entre el hiperplano de decisión y los ejemplos en el conjunto de entrenamiento.

Nota: A pesar de su nombre, LDA no pertenece a la clase de modelos discriminativos en esta taxonomía. Sin embargo, su nombre tiene sentido cuando comparamos LDA con el otro algoritmo principal de reducción de dimensionalidad lineal: análisis de componentes principales (PCA). LDA es un algoritmo de aprendizaje supervisado que utiliza las etiquetas de los datos, mientras que PCA es un algoritmo de aprendizaje no supervisado que ignora las etiquetas. Para resumir, el nombre es un artefacto histórico.

El entrenamiento discriminatorio a menudo produce mayor precisión que el modelado de las funciones de densidad condicional. Sin embargo, manejar los datos que faltan suele ser más fácil con los modelos de densidad condicional.

Todos los algoritmos de clasificación lineal enumerados anteriormente se pueden convertir en algoritmos no lineales que operan en un espacio de entrada diferente φ φ ()x→ → ){displaystyle varphi ({vec {x})}, usando el truco del núcleo.

Entrenamiento discriminatorio

La capacitación discriminatoria de los clasificadores lineales generalmente se lleva a cabo de manera supervisada, por medio de un algoritmo de optimización al que se le proporciona un conjunto de capacitación con las salidas deseadas y una función de pérdida que mide la discrepancia entre las salidas del clasificador y las salidas deseadas.. Así, el algoritmo de aprendizaje resuelve un problema de optimización de la forma

arg⁡ ⁡ minwR()w)+C.. i=1NL()Sí.i,wTxi){displaystyle {underset {Mathbf} }{gmin };R(mathbf {w})+Csum _{i=1}^{N}L(y_{i},mathbf {w} ¿Qué?

dónde

• w es un vector de parámetros clasificatorios,
• L()Sí._i, w^Tx_i) es una función de pérdida que mide la discrepancia entre la predicción del clasificador y la salida verdadera Sí._i para el i"el ejemplo de entrenamiento,
• R()w) es una función de regularización que evita que los parámetros se vuelvan demasiado grandes (causando sobrefitting), y
• C es una constante de escalar (ajustada por el usuario del algoritmo de aprendizaje) que controla el equilibrio entre la regularización y la función de pérdida.

Las funciones de pérdida populares incluyen la pérdida de bisagra (para SVM lineales) y la pérdida de registro (para regresión logística lineal). Si la función de regularización R es convexa, entonces el problema anterior es convexo. Existen muchos algoritmos para resolver tales problemas; los populares para la clasificación lineal incluyen el descenso de gradiente (estocástico), L-BFGS, el descenso de coordenadas y los métodos de Newton.