Clasificación de discontinuidades

Las funciones continuas son de suma importancia en matemáticas, funciones y aplicaciones. Sin embargo, no todas las funciones son continuas. Si una función no es continua en un punto de su dominio, se dice que tiene una discontinuidad allí. El conjunto de todos los puntos de discontinuidad de una función puede ser un conjunto discreto, un conjunto denso o incluso todo el dominio de la función.

La oscilación de una función en un punto cuantifica estas discontinuidades de la siguiente manera:

• en una discontinuidad extraíble, la distancia que el valor de la función está apagado por la oscilación;
• en una salto discontinuidad, el tamaño del salto es la oscilación (asumiendo que el valor a el punto está entre estos límites de las dos partes);
• en una discontinuidad esencial, la oscilación mide el fracaso de un límite a existir; el límite es constante.

Un caso especial es si la función diverge hacia infinito o menos infinito, en cuyo caso la oscilación no está definida (en los números reales extendidos, esta es una discontinuidad removible).

Clasificación

Para cada uno de los siguientes, considere una función de valor real ${\displaystyle f}$ de una variable real ${\displaystyle x,}$ definido en un barrio del punto ${\displaystyle x_{0}$ en que ${\displaystyle f}$ es discontinuo.

discontinuidad extraíble

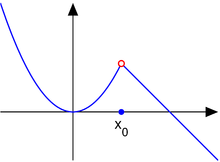
Considere la función por partes

$${\displaystyle f(x)={\begin{cases}x^{2} limit{\text{ for }}xtraducido1\0{\text{ for }}x=1\2-x limit{\text{ for }}x {\end{cases}}}}}}}}$$

El punto ${\displaystyle x_{0}=1}$ es un discontinuidad extraíble. Para este tipo de discontinuidad:

El límite unilateral de la dirección negativa:

$${\displaystyle L^{-}=\lim _{x\to x_{0} {-}f(x)}$$

$${\displaystyle L^{+}=\lim _{x\to x_{0} {+}f(x)}$$

${\displaystyle x_{0}$

${\displaystyle L=L^{-}=L^{+}$

${\displaystyle L.$

${\displaystyle f(x)}$

${\displaystyle x}$

${\displaystyle x_{0}$

${\displaystyle f\left(x_{0}\right)}$

${\displaystyle L.$

${\displaystyle x_{0}$

${\displaystyle f}$

${\displaystyle x_{0},}$

$${\displaystyle g(x)={\begin{cases}f(x) limitadax\neq x_{0}\\\L simultáneamente=x_{0}\end{cases}}$$

${\displaystyle x=x_{0}$

El término discontinuidad extraíble a veces se amplía para incluir una singularidad extraíble, en la que existen los límites en ambas direcciones y son iguales, mientras que la función no se define en el punto ${\displaystyle x_{0}$ Este uso es un abuso de terminología porque la continuidad y la discontinuidad de una función son conceptos definidos sólo para puntos en el dominio de la función.

Discontinuidad de salto

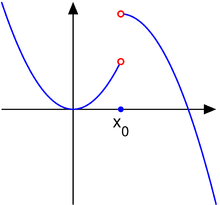
Considere la función

$${\displaystyle f(x)={\begin{cases}x^{2} {\mbox{ for }}xse hizo1\0 {\mbox{ for }}x=1\2-(x-1)}{2}} {\mbox{ for }x]$$

Entonces, el punto ${\displaystyle x_{0}=1}$ es un salto discontinuidad.

En este caso, un único límite no existe porque los límites unilaterales, ${\displaystyle L.$ y ${\displaystyle L^{+}$ existen y son finitos, pero son no igual: desde entonces, ${\displaystyle L^{-}\neq L^{+}$ el límite ${\displaystyle L.$ no existe. Entonces, ${\displaystyle x_{0}$ se llama salto discontinuidad, discontinuidad pasoo discontinuidad del primer tipo. Para este tipo de discontinuidad, la función ${\displaystyle f}$ puede tener cualquier valor ${\displaystyle x_{0}$

Discontinuidad esencial

Para una discontinuidad esencial, al menos uno de los dos límites unilaterales no existe en ${\displaystyle \mathbb {R}$. (Nota que uno o ambos límites unilaterales pueden ser ${\displaystyle \pm \infty }$).

Considere la función

$${\displaystyle f(x)={\begin{cases}\sin {\frac {5}{x-1} limit{\text{ for }}}x segnunció1\0}\0 {1}{x-1}}} {\text{ for }x Conf.1.\end{cases}}}}}$$

Entonces, el punto ${\displaystyle x_{0}=1}$ es un discontinuidad esencial.

En este ejemplo, ambos ${\displaystyle L.$ y ${\displaystyle L^{+}$ no existen en ${\displaystyle \mathbb {R}$, satisfaciendo así la condición de discontinuidad esencial. Así que... ${\displaystyle x_{0}$ es una discontinuidad esencial, discontinuidad infinita o discontinuidad del segundo tipo. (Esto es distinto de una singularidad esencial, que a menudo se utiliza al estudiar funciones de variables complejas).

Supongamos que ${\displaystyle f}$ es una función definida en un intervalo ${\displaystyle I 'subseteq \mathbb {R}$ Denotaremos ${\displaystyle D}$ el conjunto de todas las discontinuidades ${\displaystyle f}$ on ${\displaystyle I.}$ Por ${\displaystyle R.$ nos referiremos al conjunto de todos ${\displaystyle x_{0}\in I}$ tales que ${\displaystyle f}$ tiene una extraíble discontinuidad en ${\displaystyle x_{0}$ Analmente por ${\displaystyle J}$ denotamos el conjunto constituido por todos ${\displaystyle x_{0}\in I}$ tales que ${\displaystyle f}$ tiene una salto discontinuidad en ${\displaystyle x_{0}$ El conjunto de todos ${\displaystyle x_{0}\in I}$ tales que ${\displaystyle f}$ tiene una esenciales discontinuidad en ${\displaystyle x_{0}$ será denotado por ${\displaystyle E.}$ Por supuesto entonces ${\displaystyle D=R\cup J\cup E.}$

Contar discontinuidades de una función

Las dos siguientes propiedades del conjunto ${\displaystyle D}$ son relevantes en la literatura.

• El conjunto de ${\displaystyle D}$ es un ${\displaystyle F_{\sigma }$ set. El conjunto de puntos en los que una función es continua es siempre un ${\displaystyle G_{\delta }$ set (véase).
• Si en el intervalo ${\displaystyle Yo...$ ${\displaystyle f}$ es monotono entonces ${\displaystyle D}$ es a lo más contable y ${\displaystyle D=J.}$ Este es el teorema de Froda.

Tom Apostol sigue parcialmente la clasificación anterior considerando sólo las discontinuidades extraíbles y de salto. Su objetivo es estudiar la discontinuidad de las funciones monotonas, principalmente para probar el teorema de Froda. Con el mismo propósito, Walter Rudin y Karl R. Stromberg estudian también desmontables y saltan discontinuidades utilizando diferentes terminologías. Sin embargo, además, ambos autores declaran que ${\displaystyle R\cup J}$ es siempre un conjunto contable (ver).

El término discontinuidad esencial tiene evidencia de uso en el contexto matemático tan temprano como 1889. Sin embargo, el uso más temprano del término junto a una definición matemática parece haber sido dado en el trabajo por John Klippert. En ella, Klippert también clasificaba las discontinuidades esenciales por sí mismas subdividiendo el conjunto ${\displaystyle E}$ en los tres conjuntos siguientes:

$${\displaystyle E_{1}=\left\{x_{0}\in I:\lim _{x\to x_{0}{-}f(x){\text{ and }\lim _{x\to x_{0}{+}f(x){\text{ do not exist in }\mathbb {R} \right\}$$

$${\displaystyle E_{2}=\left\{x_{0}\in I: \lim _{x\to x_{0}{-}f(x){ exist in }\mathbb {R} {\text{ and }}\lim _{x\to x_{0}{+}f(x){\text{ does not exist in }}\mathbb {R}\right}$$

$${\displaystyle E_{3}=\left\{x_{0}\in Yo: \lim _{x\to x_{-} {-} {-} {\f}{\text{ no existe en }\mathbb {R} {\text{ and }}}\lim _{x\to x_{0}{+}f(x){\text{ existe in }\mathbb {R} \right\}$$

Por supuesto. ${\displaystyle E=E_{1}\cup E_{2}\cup E_{3}$ Siempre ${\displaystyle x_{0}\in E_{1},}$ ${\displaystyle x_{0}$ se llama discontinuidad esencial de primer tipo. Cualquier ${\displaystyle x_{0}\in E_{2}\cup E_{3}$ se dice un discontinuidad esencial de segundo tipo. Por lo tanto él agranda el conjunto ${\displaystyle R\cup J}$ sin perder su característica de ser contable, declarando lo siguiente:

• El set ${\displaystyle R\cup J\cup E_{2}\cup E_{3}$ es contable.

Reescribiendo el teorema de Lebesgue

Cuando ${\displaystyle I=[a,b]$ y ${\displaystyle f}$ es una función atada, es bien conocido de la importancia del conjunto ${\displaystyle D}$ en relación con la integración Riemann de ${\displaystyle f.}$ De hecho, el teorema de Lebesgue (también llamado Lebesgue-Vitali) teorema) afirma que ${\displaystyle f}$ Riemann integrado ${\displaystyle I=[a,b]$ si ${\displaystyle D}$ es un conjunto con la medida cero de Lebesgue.

En este teorema parece que todo tipo de discontinuidades tienen el mismo peso en la obstrucción que una función atada ${\displaystyle f}$ ser Riemann integrado en ${\displaystyle [a,b].}$ Puesto que los conjuntos contables son conjuntos de la medida cero de Lebesgue y una unión contable de conjuntos con la medida cero de Lebesgue sigue siendo un conjunto de la medida cero de Lebesgue, estamos viendo ahora que este no es el caso. De hecho, las discontinuidades en el conjunto ${\displaystyle R\cup J\cup E_{2}\cup E_{3}$ son absolutamente neutrales en cuanto a la integración Riemann de ${\displaystyle f.}$ Las principales discontinuidades para ese propósito son las discontinuidades esenciales de primer tipo y, en consecuencia, el teorema Lebesgue-Vitali puede ser reescrito como sigue:

• Una función atada, ${\displaystyle f,}$ Riemann integrado ${\displaystyle [a,b]}$ si y sólo si el corresponsal ${\displaystyle E_{1}$ de todas las discontinuidades esenciales de primer tipo ${\displaystyle f}$ Tiene la medida cero de Lebesgue.

El caso donde ${\displaystyle E_{1}=\varnothing }$ corresponden a las siguientes situaciones clásicas complementarias bien conocidas de Riemann la integración de una función atada ${\displaystyle f:[a,b]\to \mathbb {R}$:

• Si ${\displaystyle f}$ tiene límite de mano derecha en cada punto ${\displaystyle [a,b]$ entonces ${\displaystyle f}$ Riemann integrado ${\displaystyle [a,b]}$ (véase)
• Si ${\displaystyle f}$ tiene límite izquierdo en cada punto ${\displaystyle]a,b}$ entonces ${\displaystyle f}$ Riemann integrado ${\displaystyle [a,b].}$
• Si ${\displaystyle f}$ es una función regulada ${\displaystyle [a,b]}$ entonces ${\displaystyle f}$ Riemann integrado ${\displaystyle [a,b].}$

Ejemplos

La función de Thomae es discontinua en todo punto racional distinto de cero, pero continua en todo punto irracional. Se ve fácilmente que todas esas discontinuidades son eliminables. Según el primer párrafo, no existe una función que sea continua en todo punto racional, pero sí discontinua en todo punto irracional.

La función indicadora de los racionales, también conocida como función de Dirichlet, es discontinua en todas partes. Estas discontinuidades son todas esenciales también del primer tipo.

Considere ahora el Cantor ternario $[0,1]$ y su función indicadora (o característica)

$${\displaystyle \mathbf {1} _{\mathcal {C}(x)={\begin{cases}1 golpex\in {\fnMitcal {\fnMitcal}\0,1}\setminus {\mátcal}\0 {C}.\end{cases}}$$

${\displaystyle {\fnMithcal}}$

${\fnMicrosoft {\fnMitcal} {C}:= ¿Qué? }C_{n}$

${\displaystyle C_{n}$

$${\displaystyle C_{n}={\frac {C_{n-1}{3}}\cup \left({\frac {2}{3}+{\frac} {C_{n-1}} {\fn\fn\fn\fn\fn\fn\fn\fn\fn1} {\fn\fn\fn\fn\fn1} {\fn\fnMicrosoft Sans Serif} {\fnMicrosoft Sans Serif} {\fnMicrosoft Sans Serif} {\f}}}}}\fn\fn\fn\fn\fn\fn\fn\fn\fnK\fnK\fn\fnK\fn\fn\fn\fn\fn\fn\fn\fn\fn\fn\fn\fn\fn\fn\fn\fn\fn\fn\fn\fn\fn\fn\fn\fn\fn\fn\fn\fn\fn\fn\fn\fn\fn\fn\fn\fn\fn\fn$$

En vista de las interrupciones de la función ${\displaystyle \mathbf {1} _{\mathcal {C}(x),}$ Vamos a asumir un punto ${\displaystyle x_{0}\not \in {\mathcal {C}}$

Por lo tanto existe un conjunto ${\displaystyle C_{n}$ utilizado en el formulación de ${\displaystyle {\fnMithcal}}$, que no contiene ${\displaystyle x_{0}$ Eso es, ${\displaystyle x_{0}$ pertenece a uno de los intervalos abiertos que fueron removidos en la construcción de ${\displaystyle C_{n}$ Por aquí, ${\displaystyle x_{0}$ tiene un barrio sin puntos ${\displaystyle {\mathcal {}}$ (De otra manera, la misma conclusión sigue teniendo en cuenta que ${\displaystyle {\fnMithcal}}$ es un conjunto cerrado y por lo tanto su complemento con respecto a ${\displaystyle [0,1]}$ está abierto). Por lo tanto ${\displaystyle \mathbf {1} {C}}$ sólo asume el valor cero en algunos barrios ${\displaystyle x_{0}$ Por lo tanto ${\displaystyle \mathbf {1} {C}}$ es continuo ${\displaystyle x_{0}$

Esto significa que el conjunto ${\displaystyle D}$ de todas las discontinuidades ${\displaystyle \mathbf {1} {C}}$ en el intervalo ${\displaystyle [0,1]}$ es un subconjunto de ${\displaystyle {\mathcal {}}$ Desde ${\displaystyle {\fnMithcal}}$ es un conjunto incontable con la medida null Lebesgue, también ${\displaystyle D}$ es una medida de Lebesgue nula establecida y por lo tanto en el aspecto de Lebesgue-Vitali theorem ${\displaystyle \mathbf {1} {C}}$ es una función integradora Riemann.

Más precisamente uno tiene ${\displaystyle D={\fnMitcal {C}}$ De hecho, desde ${\displaystyle {\fnMithcal}}$ es un conjunto denso no, si ${\displaystyle x_{0}\in {\fnMithcal {C}}$ entonces no hay barrio ${\displaystyle \left(x_{0}-\varepsilonx_{0}+\varepsilon \right)}$ de ${\displaystyle x_{0},}$ se puede incluir en ${\displaystyle {\mathcal {}}$ Por aquí, cualquier barrio ${\displaystyle x_{0}\in {\fnMithcal {C}}$ contiene puntos ${\displaystyle {\fnMithcal}}$ y puntos que no son de ${\displaystyle {\mathcal {}}$ En términos de la función ${\displaystyle \mathbf {1} {C}}$ esto significa que ambos ${\textstyle \lim _{x\to ¿Qué?$ y ${\textstyle \lim _{x\to x_{0}{+}1_{\mathcal {C}(x)}$ no existen. Eso es, ${\displaystyle D=E_{1},}$ Donde ${\displaystyle E_{1},}$ como antes, denotamos el conjunto de todas las discontinuidades esenciales de primer tipo de la función ${\displaystyle \mathbf {1} {C}}$ Claramente ${\textstyle \int _{0}\mathbf {1} _{\mathcal {C}(x)dx=0.}$

Discontinuidades de derivados

Vamos. ${\displaystyle I 'subseteq \mathbb {R}$ un intervalo abierto y${\displaystyle f:I\to \mathbb {R}$ el derivado de una función, ${\displaystyle F:I\to \mathbb {R}$, diferenciable en ${\displaystyle I}$. Eso es, ${\displaystyle F'(x)=f(x)}$ para todos ${\displaystyle x\in I}$.

Es bien conocido que según el Teorema de Darboux la función derivada ${\displaystyle f:I\to \mathbb {R}$ tiene la restricción de satisfacer la propiedad de valor intermedio.

${\displaystyle f}$ puede por supuesto ser continuo en el intervalo ${\displaystyle I}$. Recordemos que cualquier función continua, por el teorema de Bolzano, satisface la propiedad de valor intermedio.

Por otro lado, la propiedad de valor intermedio no impide ${\displaystyle f}$ de tener discontinuidades en el intervalo ${\displaystyle I}$. Pero el teorema de Darboux tiene una consecuencia inmediata en el tipo de discontinuidades que ${\displaystyle f}$ puede haberlo hecho. De hecho, si ${\displaystyle x_{0}\in I}$ es un punto de discontinuidad ${\displaystyle f}$, entonces necesariamente ${\displaystyle x_{0}$ es una discontinuidad esencial ${\displaystyle f}$.

Esto significa en particular que las dos situaciones siguientes no pueden ocurrir:

Además, hay que excluir otras dos situaciones (véase John Klippert):

Observe que cuando una de las condiciones i), ii), iii), o iv) se cumple para algunos ${\displaystyle x_{0}\in I}$ uno puede concluir que ${\displaystyle f}$ no posee un antiderivativo, ${\displaystyle F}$, en el intervalo ${\displaystyle I}$.

Por otro lado, un nuevo tipo de discontinuidad con respecto a cualquier función ${\displaystyle f:I\to \mathbb {R}$ se puede introducir: una discontinuidad esencial, ${\displaystyle x_{0}\in I}$, de la función ${\displaystyle f}$, se dice que es un discontinuidad esencial de ${\displaystyle f}$ si

$${\displaystyle \lim _{x\to x_{0}{-}f(x)\neq \pm \infty }$$

$${\displaystyle \lim _{x\to x_{0}{+}f(x)\neq \pm \infty.}$$

Por lo tanto si ${\displaystyle x_{0}\in I}$ es una discontinuidad de una función derivada ${\displaystyle f:I\to \mathbb {R}$, entonces necesariamente ${\displaystyle x_{0}$ es una discontinuidad esencial ${\displaystyle f}$.

Note también que cuando ${\displaystyle I=[a,b]$ y ${\displaystyle f:I\to \mathbb {R}$ es una función atada, como en las suposiciones del teorema de Lebesgue, tenemos para todos ${\displaystyle x_{0}\in (a,b)}$:

$${\displaystyle \lim _{x\to x_{0}{\pm}f(x)\neq \pm \infty}$$

$${\displaystyle \lim _{x\to a^{+}f(x)\neq \pm \infty}$$

$${\displaystyle \lim _{x\to b^{-}f(x)\neq \pm \infty.}$$

${\displaystyle f}$