Clase de equivalencia

La congruencia es un ejemplo de relación de equivalencia. Los dos triángulos más izquierdos son congruentes, mientras que los triángulos tercero y cuarto no son congruentes con cualquier otro triángulo mostrado aquí. Así, los dos primeros triángulos están en la misma clase de equivalencia, mientras que los triángulos tercero y cuarto son cada uno en su propia clase de equivalencia.

En matemáticas, cuando los elementos de algunos conjuntos S{displaystyle S. tener una noción de equivalencia (formalizada como una relación de equivalencia), entonces se puede dividir naturalmente el conjunto S{displaystyle S. en Clases de equivalencia. Estas clases de equivalencia se construyen para que elementos a{displaystyle a} y b{displaystyle b} pertenecen al mismo Clase de equivalencia si, y sólo si, son equivalentes.

Formalmente, dado un conjunto S{displaystyle S. y una relación de equivalencia ♪ ♪ {displaystyle ,sim ,} on S,{displaystyle S,} el Clase de equivalencia de un elemento a{displaystyle a} dentro S,{displaystyle S,} denotado por [a],{displaystyle [a],} es el conjunto

{}x▪ ▪ S:x♪ ♪ a}{displaystyle {xin S:xsim a}

a.{displaystyle a.}

S.{displaystyle S.}

S{displaystyle S.

♪ ♪ ,{displaystyle ,sim ,}

S/♪ ♪ .{displaystyle S/sim.}

Cuando el conjunto S{displaystyle S. tiene alguna estructura (como una operación de grupo o una topología) y la relación de equivalencia ♪ ♪ {displaystyle ,sim ,} es compatible con esta estructura, el conjunto de cocientes suele heredar una estructura similar de su conjunto padre. Ejemplos incluyen espacios cocientes en álgebra lineal, espacios cocientes en topología, grupos cocientes, espacios homogéneos, anillos cocientes, monoides cocientes y categorías cocientes.

Ejemplos

• Si X{displaystyle X} es el conjunto de todos los coches, y ♪ ♪ {displaystyle ,sim ,} es la relación de equivalencia "tiene el mismo color que", entonces una clase de equivalencia particular consistiría de todos los coches verdes, y X/♪ ♪ {displaystyle X/sim} podría ser identificado naturalmente con el conjunto de todos los colores del coche.
• Vamos X{displaystyle X} ser el conjunto de todos los rectángulos en un plano, y ♪ ♪ {displaystyle ,sim ,} la relación de equivalencia "tiene el mismo área que", entonces para cada número real positivo A,{displaystyle A,} habrá una clase de equivalencia de todos los rectángulos que tienen área A.{displaystyle A.}
• Considere el modulo 2 relación de equivalencia en el conjunto de enteros, Z,{displaystyle mathbb {Z} tales que x♪ ♪ Sí.{displaystyle xsim y} si y sólo si su diferencia x− − Sí.{displaystyle x-y} es un número uniforme. Esta relación da lugar a exactamente dos clases de equivalencia: una clase consiste en todos los números, y la otra clase consiste en todos los números impares. Usando corchetes alrededor de un miembro de la clase para denotar una clase de equivalencia bajo esta relación, [7],[9],{displaystyle [7],[9],} y [1]{displaystyle [1] todos representan el mismo elemento Z/♪ ♪ .{displaystyle mathbb {Z} /sim.}
• Vamos X{displaystyle X} ser el conjunto de pares ordenados de enteros ()a,b){displaystyle (a,b)} con no cero b,{displaystyle b,} y definir una relación de equivalencia ♪ ♪ {displaystyle ,sim ,} on X{displaystyle X} tales que ()a,b)♪ ♪ ()c,d){displaystyle (a,b)sim (c,d)} si ad=bc,{displaystyle ad=bc,} entonces la clase de equivalencia del par ()a,b){displaystyle (a,b)} se puede identificar con el número racional a/b,{displaystyle a/b,} y esta relación de equivalencia y sus clases de equivalencia pueden utilizarse para dar una definición formal del conjunto de números racionales. La misma construcción se puede generalizar al campo de fracciones de cualquier dominio integral.
• Si X{displaystyle X} consiste en todas las líneas en, digamos, el plano Euclideano, y L♪ ♪ M{displaystyle Lsim M} significa que L{displaystyle L. y M{displaystyle M} son líneas paralelas, entonces el conjunto de líneas que son paralelas entre sí forman una clase de equivalencia, siempre y cuando una línea se considere paralela a sí misma. En esta situación, cada clase de equivalencia determina un punto en el infinito.

Definición y notación

Relación de equivalencia en un conjunto X{displaystyle X} es una relación binaria ♪ ♪ {displaystyle ,sim ,} on X{displaystyle X} satisfacción de las tres propiedades:

• a♪ ♪ a{displaystyle asim a} para todos a▪ ▪ X{displaystyle ain X} (reflexividad),
• a♪ ♪ b{displaystyle asim b} implicación b♪ ♪ a{displaystyle bsim a} para todos a,b▪ ▪ X{displaystyle a,bin X} (simetría),
• si a♪ ♪ b{displaystyle asim b} y b♪ ♪ c{displaystyle bsim c} entonces a♪ ♪ c{displaystyle asim c} para todos a,b,c▪ ▪ X{displaystyle a,b,cin X} (transitividad).

La clase de equivalencia de un elemento a{displaystyle a} a menudo se denota [a]{displaystyle [a]} o [a]♪ ♪ ,{displaystyle [a]_{sim},} y se define como el conjunto {}x▪ ▪ X:a♪ ♪ x}{displaystyle {xin X:asim x} de elementos relacionados con a{displaystyle a} por♪ ♪ .{displaystyle ,sim.} La palabra "clase" en el término "clase de igualdad" puede considerarse generalmente como un sinónimo de "set", aunque algunas clases de equivalencia no son sets sino clases adecuadas. Por ejemplo, "ser isomorfo" es una relación de equivalencia en grupos, y las clases de equivalencia, llamadas clases de isomorfismo, no son conjuntos.

El conjunto de todas las clases de equivalencia en X{displaystyle X} con respecto a una relación de equivalencia R{displaystyle R. es denotado como X/R,{displaystyle X/R,} y se llama X{displaystyle X} modulo R{displaystyle R. (o el Conjunto de referencia de X{displaystyle X} por R{displaystyle R.). El mapa subjetivo x↦ ↦ [x]{displaystyle xmapsto [x]} desde X{displaystyle X} sobre X/R,{displaystyle X/R,} que mapea cada elemento a su clase de equivalencia, se llama subjeción canónica, o el proyección canónica.

Cada elemento de una clase de equivalencia caracteriza a la clase, y puede ser utilizado para Representación Es. Cuando tal elemento es elegido, se llama representante de la clase. La elección de un representante en cada clase define una inyección de X/R{displaystyle X/R} a X. Puesto que su composición con la subjeción canónica es la identidad de X/R,{displaystyle X/R,} tal inyección se llama sección, al utilizar la terminología de la teoría de la categoría.

A veces, hay una sección más "natural" que las otras. En este caso, se llama a los representantes canonical representatives. Por ejemplo, en aritmética modular, para cada entero m más grande que 1, el modulo m de congruencia es una relación de equivalencia en los enteros, para los cuales dos enteros a y b son equivalentes en este caso, uno dice congruente —si m divideciones a− − b;{displaystyle a-b;} Esto es denotado a↑ ↑ b()modm).{textstyle aequiv b{pmod {m}} Cada clase contiene un entero no negativo único más pequeño que m,{displaystyle m,} y estos enteros son los representantes canónicos.

El uso de representantes para representar clases permite evitar considerar explícitamente las clases como conjuntos. En este caso, la subjeción canónica que mapea un elemento a su clase es reemplazada por la función que mapea un elemento al representante de su clase. En el ejemplo anterior, esta función se denota amodm,{displaystyle a{bmod {m}} y produce el resto de la división euroclidiana a por m.

Propiedades

Cada elemento x{displaystyle x} de X{displaystyle X} es miembro de la clase de equivalencia [x].{displaystyle [x].} Cada dos clases de equivalencia [x]{displaystyle [x]} y [Sí.]{displaystyle [y]} son iguales o descomunales. Por lo tanto, el conjunto de todas las clases de equivalencia X{displaystyle X} forma una partición de X{displaystyle X}: cada elemento de X{displaystyle X} pertenece a una y única clase de equivalencia. Por el contrario, cada partición de X{displaystyle X} viene de una relación de equivalencia de esta manera, según la cual x♪ ♪ Sí.{displaystyle xsim y} si x{displaystyle x} y Sí.{displaystyle y} pertenece al mismo conjunto de la partición.

De las propiedades de una relación de equivalencia se sigue que

x♪ ♪ Sí.{displaystyle xsim y}

[x]=[Sí.].{displaystyle [x]=[y].}

En otras palabras, si ♪ ♪ {displaystyle ,sim ,} es una relación de equivalencia en un conjunto X,{displaystyle X. y x{displaystyle x} y Sí.{displaystyle y} son dos elementos X,{displaystyle X. entonces estas declaraciones son equivalentes:

• x♪ ♪ Sí.{displaystyle xsim y}
• [x]=[Sí.]{displaystyle [x]=[y]}
• [x]∩ ∩ [Sí.]ل ل ∅ ∅ .{displaystyle [x]cap [y]neq emptyset.}

Representación gráfica

Gráfico de una equivalencia de ejemplo con 7 clases

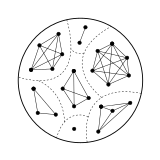
Un gráfico no dirigido puede estar asociado a cualquier relación simétrica en un conjunto X,{displaystyle X. donde los vértices son los elementos X,{displaystyle X. y dos vértices s{displaystyle s} y t{displaystyle t} se unen si y sólo si s♪ ♪ t.{displaystyle ssim t.} Entre estos gráficos se encuentran los gráficos de las relaciones de equivalencia; se caracterizan como los gráficos tales que los componentes conectados son camarillas.

Invariantes

Si ♪ ♪ {displaystyle ,sim ,} es una relación de equivalencia X,{displaystyle X. y P()x){displaystyle P(x)} es una propiedad de elementos X{displaystyle X} tal como sea x♪ ♪ Sí.,{displaystyle xsim y,} P()x){displaystyle P(x)} es verdad P()Sí.){displaystyle P(y)} es verdad, entonces la propiedad P{displaystyle P} se dice que es un invariante ♪ ♪ ,{displaystyle ,sim ,} o bien definido bajo la relación ♪ ♪ .{displaystyle ,sim.}

Un caso particular frecuente ocurre cuando f{displaystyle f} es una función X{displaystyle X} a otro conjunto Y{displaystyle Sí.; si f()x1)=f()x2){displaystyle fleft(x_{1}right)=fleft(x_{2}right)} siempre x1♪ ♪ x2,{displaystyle x_{1}sim x_{2} entonces f{displaystyle f} se dice que Clase invariable bajo ♪ ♪ ,{displaystyle ,sim ,} o simplemente invariable under ♪ ♪ .{displaystyle ,sim.} Esto ocurre, por ejemplo, en la teoría del carácter de los grupos finitos. Algunos autores utilizan "compatible con ♪ ♪ {displaystyle ,sim ,}"o simplemente "respetos" ♪ ♪ {displaystyle ,sim ,}"en vez de "invariante bajo ♪ ♪ {displaystyle ,sim ,}".

Cualquier función f:X→ → Y{displaystyle f:Xto Sí. es Clase invariable bajo ♪ ♪ ,{displaystyle ,sim ,} según cuál x1♪ ♪ x2{displaystyle x_{1}sim x_{2} si f()x1)=f()x2).{displaystyle fleft(x_{1}right)=fleft(x_{2}right). } La clase de equivalencia x{displaystyle x} es el conjunto de todos los elementos en X{displaystyle X} que se mapean a f()x),{displaystyle f(x),} es decir, la clase [x]{displaystyle [x]} es la imagen inversa de f()x).{displaystyle f(x).} Esta relación de equivalencia se conoce como el núcleo f.{displaystyle f.}

Más generalmente, una función puede mapear argumentos equivalentes (bajo una relación de equivalencia ♪ ♪ X{displaystyle sim _{X}} on X{displaystyle X}) a valores equivalentes (bajo una relación de equivalencia ♪ ♪ Y{displaystyle sim _{Y}} on Y{displaystyle Sí.). Tal función es un morfismo de conjuntos equipados con una relación de equivalencia.

Espacio cociente en topología

En topología, un espacio de cociente es un espacio topológico formado en el conjunto de clases de equivalencia de una relación de equivalencia en un espacio topológico, utilizando la topología del espacio original para crear la topología en el conjunto de clases de equivalencia.

En álgebra abstracta, las relaciones de congruencia en el conjunto subyacente de un álgebra permiten que el álgebra induzca un álgebra en las clases de equivalencia de la relación, denominada álgebra de cociente. En álgebra lineal, un espacio de cociente es un espacio vectorial formado al tomar un grupo de cociente, donde el homomorfismo del cociente es un mapa lineal. Por extensión, en álgebra abstracta, el término espacio de cociente puede usarse para módulos de cociente, anillos de cociente, grupos de cociente o cualquier álgebra de cociente. Sin embargo, el uso del término para los casos más generales puede ser a menudo por analogía con las órbitas de una acción de grupo.

Las órbitas de una acción de grupo sobre un conjunto pueden denominarse espacio cociente de la acción sobre el conjunto, particularmente cuando las órbitas de la acción de grupo son las clases laterales derechas de un subgrupo de un grupo, que surgen de la acción de el subgrupo en el grupo por traslaciones a la izquierda, o respectivamente las clases laterales izquierdas como órbitas bajo traslación a la derecha.

Un subgrupo normal de un grupo topológico, que actúa sobre el grupo por acción de traslación, es un espacio cociente en los sentidos de topología, álgebra abstracta y acciones de grupo simultáneamente.

Aunque el término se puede utilizar para el conjunto de clases de equivalencia de cualquier relación de equivalencia, posiblemente con otra estructura, la intención de utilizar el término es generalmente para comparar ese tipo de relación de equivalencia en un conjunto X,{displaystyle X. o a una relación de equivalencia que induce alguna estructura en el conjunto de clases de equivalencia de una estructura del mismo tipo X,{displaystyle X. o a las órbitas de una acción grupal. Tanto el sentido de una estructura preservada por una relación de equivalencia, como el estudio de los invariantes bajo acciones de grupo, conducen a la definición de invariantes de relaciones de equivalencia dadas anteriormente.