Circunvolución

ImprimirCitar

Expresar la cantidad de solapamiento de una función mientras se desplaza sobre otra

Comparación visual de convolución, cruza-correlación y autocorrelación. Para las operaciones relacionadas con la función

f

, y asumiendo la altura de

f

es 1.0, el valor del resultado no a 5 puntos diferentes se indica por el área sombreada debajo de cada punto. La simetría de

f

es la razón

f*g

fstar g

son idénticos en este ejemplo.

En matemáticas (en particular, análisis funcionales), convolution es una operación matemática en dos funciones ( $f$ y $g$ ) que produce una tercera función ( $f*g$ ) que expresa cómo la forma de uno es modificada por el otro. El término convolution se refiere tanto a la función de resultado como al proceso de cálculo. Se define como la parte integral del producto de las dos funciones después de que uno se refleje en el eje y y y cambiado. La elección de qué función se refleja y cambia antes de que la integral no cambie el resultado integral (véase la conmutación). La integral es evaluada para todos los valores de cambio, produciendo la función convolutiva.

Algunas características de la convolución son similares a la cruza-correlación: para funciones de valor real, de una variable continua o discreta, convolution ( $f*g$ ) difiere de la cruza-correlación ( $fstar g$ Sólo en eso $f () x)$ o $g () x)$ se refleja en el eje y en la convolución, por lo que es una cruz-correlación $g () - x)$ y $f () x)$ , o $f () - x)$ y $g () x)$ . Para funciones de valor complejo, el operador de intercorrelación es el conjunto del operador de convolución.

La convolución tiene aplicaciones que incluyen probabilidad, estadística, acústica, espectroscopia, procesamiento de señales e imágenes, geofísica, ingeniería, física, visión artificial y ecuaciones diferenciales.

La convolución se puede definir para funciones en el espacio euclidiano y otros grupos (como estructuras algebraicas). Por ejemplo, las funciones periódicas, como la transformada de Fourier de tiempo discreto, se pueden definir en un círculo y convolucionar mediante convolución periódica. (Consulte la fila 18 en DTFT § Properties.) Se puede definir una convolución discreta para funciones en el conjunto de enteros.

Las generalizaciones de la convolución tienen aplicaciones en el campo del análisis numérico y el álgebra lineal numérica, y en el diseño e implementación de filtros de respuesta de impulso finitos en el procesamiento de señales.

El cálculo de la inversa de la operación de convolución se conoce como deconvolución.

Definición

La convolución de $f$ y $g$ se escribe $f * g$ , denotando al operador con el símbolo $*$ . Se define como la integral del producto de las dos funciones después de que una se refleja sobre el eje y y se desplaza. Como tal, es un tipo particular de transformada integral:

{displaystyle (f*g)(t):=int _{-infty }^{infty }f(tau)g(t-tau),dtau.}

Una definición equivalente es (ver conmutatividad):

{displaystyle (f*g)(t):=int _{-infty }^{infty }f(t-tau)g(tau),dtau.}

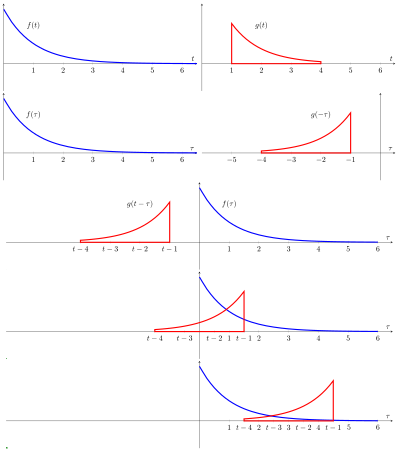
Mientras que el símbolo $t$ se utiliza anteriormente, no necesita representar el dominio del tiempo. A cada uno t, la fórmula de la convolución se puede describir como el área bajo la función $f () τ)$ ponderado por la función $g () - τ)$ cambiada por la cantidad $t$ . As $t$ cambios, la función de ponderación $g () t - τ)$ enfatiza diferentes partes de la función de entrada $f () τ)$ ; Si $t$ es un valor positivo, entonces $g () t - τ)$ es igual a $g () - τ)$ que se desliza o se desplaza a lo largo de la $tau$ -eje hacia la derecha (a la derecha) $+$ ) por la cantidad de $t$ , mientras que si $t$ es un valor negativo, entonces $g () t - τ)$ es igual a $g () - τ)$ que se desliza o se desplaza hacia la izquierda (a la izquierda) $- ¡No!$ ) por la cantidad de $Silencio$ .

Para las funciones $f$ , $g$ admitido solo en $[0, \infty]$ (es decir, cero para argumentos negativos), los límites de integración se pueden truncar, lo que da como resultado:

{displaystyle (f*g)(t)=int _{0}^{t}f(tau)g(t-tau),dtau quad {text{for }}f,g:[0,infty)to mathbb {R}.}

Para la formulación multidimensional de convolución, consulte dominio de definición (abajo).

Notación

Una convención notacional de ingeniería común es:

{displaystyle f(t)*g(t)mathrel {:=} underbrace {int _{-infty }^{infty }f(tau)g(t-tau),dtau } _{(f*g)(t)},}

que debe interpretarse con cuidado para evitar confusiones. Por ejemplo, $f (t)* g (t - t 0)$ es equivalente a $(f * g)(t - t 0)$ , pero $f (t - t 0)* g (t - t 0)$ es de hecho equivalente a $(f * g)(t - 2 t 0)$ .

Relaciones con otras transformaciones

Dados dos funciones ${displaystyle f(t)}$ y $g(t)$ con transformaciones bilaterales de Laplace (transforma de dos caras de Laplace)

{displaystyle F(s)=int _{-infty }^{infty }e^{-su} f(u) {text{d}}u}

{displaystyle G(s)=int _{-infty }^{infty }e^{-sv} g(v) {text{d}}v}

respectivamente, la operación de convolución ${displaystyle f(t)*g(t)}$ se puede definir como la transformación inversa de Laplace del producto de ${displaystyle F(s)}$ y ${displaystyle G(s)}$ . Más precisamente,

{displaystyle {begin{aligned}F(s)cdot G(s)&=int _{-infty }^{infty }e^{-su} f(u) {text{d}}ucdot int _{-infty }^{infty }e^{-sv} g(v) {text{d}}v\&=int _{-infty }^{infty }int _{-infty }^{infty }e^{-s(u+v)} f(u) g(v) {text{d}}u {text{d}}vend{aligned}}}

Vamos ${displaystyle t=u+v}$ tales que

{displaystyle {begin{aligned}F(s)cdot G(s)&=int _{-infty }^{infty }int _{-infty }^{infty }e^{-st} f(u) g(t-u) {text{d}}u {text{d}}t\&=int _{-infty }^{infty }e^{-st}underbrace {int _{-infty }^{infty }f(u) g(t-u) {text{d}}u} _{f(t)*g(t)} {text{d}}t\&=int _{-infty }^{infty }e^{-st}(f(t)*g(t)) {text{d}}tend{aligned}}}

Note que ${displaystyle F(s)cdot G(s)}$ es la transformación bilateral de Laplace ${displaystyle f(t)*g(t)}$ . Una derivación similar se puede hacer utilizando la transformación unilateral de Laplace (transforma de Laplace unilateral).

La operación de convolución también describe la salida (en términos de la entrada) de una importante clase de operaciones conocidas como invariantes en el tiempo lineales (LTI). Consulte la teoría del sistema LTI para obtener una derivación de la convolución como resultado de las restricciones LTI. En términos de las transformadas de Fourier de la entrada y salida de una operación LTI, no se crean nuevos componentes de frecuencia. Los existentes sólo se modifican (amplitud y/o fase). En otras palabras, la transformada de salida es el producto puntual de la transformada de entrada con una tercera transformada (conocida como función de transferencia). Consulte el teorema de convolución para obtener una derivación de esa propiedad de convolución. Por el contrario, la convolución se puede derivar como la transformada inversa de Fourier del producto puntual de dos transformadas de Fourier.

Explicación visual

Expresar cada función en términos de una variable muñeca $tau.$ Reflejar una de las funciones: $g(tau)$ → $g(-tau).$ Añadir un tiempo-offset $t$ , que permite ${displaystyle g(-tau)}$ para deslizarse a lo largo de $tau$ -Eje. Si $t$ es un valor positivo, entonces $g(t-tau)$ es igual a ${displaystyle g(-tau)}$ que se desliza o se desplaza a lo largo de la $tau$ -eje hacia la derecha (a la derecha) $+$ ) por la cantidad de $t$ . Si $t$ es un valor negativo, entonces $g(t-tau)$ es igual a ${displaystyle g(-tau)}$ que se desliza o se desplaza hacia la izquierda (a la izquierda) $- ¡No!$ ) por la cantidad de Silencio $t$ Silencio. Comienzo $t$ a $JUEGO$ y deslizarlo todo el camino $+$ . Dondequiera que las dos funciones intersecten, encuentre la integral de su producto. En otras palabras, a tiempo $t$ , computar el área bajo la función $f(tau)$ ponderado por la función de ponderación ${displaystyle g(t-tau).}$ La forma de onda resultante (no se muestra aquí) es la evolución de las funciones $f$ y $g$ . Si $f () t)$ es un impulso unitario, el resultado de este proceso es simplemente $g () t)$ . Formally: ${displaystyle int _{-infty }^{infty }delta (tau)g(t-tau),dtau =g(t)}$
En este ejemplo, el "pulso" de color rojo ${displaystyle g(tau),}$ es una función uniforme ${displaystyle ( g(-tau)=g(tau)),}$ por lo que la convolución es equivalente a la correlación. Una instantánea de este "movie" muestra funciones ${displaystyle g(t-tau)}$ y $f(tau)$ (en azul) por algún valor del parámetro $t,$ que se define arbitrariamente como la distancia a lo largo de la $tau$ eje desde el punto $tau = 0$ al centro del pulso rojo. La cantidad de amarillo es la zona del producto ${displaystyle f(tau)cdot g(t-tau),}$ computed by the convolution/correlation integral. La película se crea cambiando continuamente $t$ y recomputando la integral. El resultado (shown in black) es una función de $t,$ pero está trazado en el mismo eje que $tau,$ para comodidad y comparación.
En esta representación, $f(tau)$ podría representar la respuesta de un circuito RC a un pulso estrecho que ocurre en ${displaystyle tau =0.}$ En otras palabras, si ${displaystyle g(tau)=delta (tau),}$ el resultado de la convolución es sólo $f(t).$ Pero cuando $g(tau)$ es el pulso más ancho (en rojo), la respuesta es una versión "smeared" de $f(t).$ Empieza en ${displaystyle t=-0.5,}$ porque definimos $t$ como la distancia de $tau = 0$ eje al centro del pulso ancho (en lugar del borde principal).

Desarrollos históricos

Uno de los primeros usos de la integral de convolución apareció en la derivación de D'Alembert del teorema de Taylor en Recherches sur différents points importants du système du monde, publicado en 1754.

También, una expresión del tipo:

{displaystyle int f(u)cdot g(x-u),du}

es utilizado por Sylvestre François Lacroix en la página 505 de su libro titulado Tratado sobre diferencias y series, que es el último de 3 volúmenes de la serie enciclopédica: Traité du calcul différentiel et du cálculo integral, Chez Courcier, París, 1797–1800. Poco después, las operaciones de convolución aparecen en las obras de Pierre Simon Laplace, Jean-Baptiste Joseph Fourier, Siméon Denis Poisson y otros. El término en sí no se generalizó hasta la década de 1950 o 1960. Antes de eso, a veces se lo conocía como Faltung (que significa plegado en alemán), producto de composición, integral de superposición, y la integral de Carson. Sin embargo, aparece ya en 1903, aunque la definición es bastante desconocida en usos más antiguos.

La operación:

<math alttext="{displaystyle int _{0}^{t}varphi (s)psi (t-s),ds,quad 0leq t∫ ∫ 0tφ φ ()s)↑ ↑ ()t− − s)ds,0≤ ≤ t.JUEGO JUEGO ,{displaystyle int _{0}varphi (s)psi (t-s),ds,quad 0leq t madeinfty}<img alt="{displaystyle int _{0}^{t}varphi (s)psi (t-s),ds,quad 0leq t

es un caso particular de productos de composición considerados por el matemático italiano Vito Volterra en 1913.

Convolución circular

Cuando una función $g T$ es periódica, con período $T$ , luego para funciones, $f$ , tal que $f * g T$ existe, la convolución también es periódica e idéntica a:

(f*g_{T})(t)equiv int _{t_{0}}^{t_{0}+T}left[sum _{k=-infty }^{infty }f(tau +kT)right]g_{T}(t-tau),dtau

donde $t 0$ es una elección arbitraria. La sumatoria se denomina sumatoria periódica de la función $f$ .

Cuando $g T$ es una suma periódica de otra función, $g$ , entonces $f * g T$ se conoce como una convolución circular o cíclica de f y $g$ .

Y si la suma periódica anterior se reemplaza por $f T$ , la operación se denomina convolución periódica de $f T$ y g_T.

Convolución discreta

Discreta 2D Convolution Animation

Para funciones de valor complejo $f, g$ definidas en el conjunto Z de enteros, la convolución discreta de $f$ y $g$ está dada por:

{displaystyle (f*g)[n]=sum _{m=-infty }^{infty }f[m]g[n-m],}

o de manera equivalente (ver conmutatividad) por:

{displaystyle (f*g)[n]=sum _{m=-infty }^{infty }f[n-m]g[m].}

La convolución de dos sucesiones finitas se define extendiendo las sucesiones a funciones con soporte finito en el conjunto de enteros. Cuando las sucesiones son los coeficientes de dos polinomios, entonces los coeficientes del producto ordinario de los dos polinomios son la convolución de las dos sucesiones originales. Esto se conoce como el producto de Cauchy de los coeficientes de las sucesiones.

Así cuando $g$ tiene soporte finito en el conjunto ${-M,-M+1,dotsM-1,M}$ (representando, por ejemplo, una respuesta de impulso finito), se puede utilizar una suma finita:

{displaystyle (f*g)[n]=sum _{m=-M}^{M}f[n-m]g[m].}

Convolución discreta circular

Cuando una función $g N$ es periódica, con punto $N$ , luego para funciones, $f$ , tal que $f * g N$ existe, la convolución también es periódica e idéntica a:

{displaystyle (f*g_{N})[n]equiv sum _{m=0}^{N-1}left(sum _{k=-infty }^{infty }{f}[m+kN]right)g_{N}[n-m].}

La sumatoria en $k$ se denomina sumatoria periódica de la función $f$ .

Si $g N$ es una suma periódica de otra función, $g$ , luego $f * g N$ se conoce como una convolución circular de $f$ y $g$ .

Cuando las duraciones distintas de cero de $f$ y $g$ están limitadas al intervalo $[0, N - 1]$ , $f * g N$ se reduce a estas formas comunes:

{displaystyle {begin{aligned}left(f*g_{N}right)[n]&=sum _{m=0}^{N-1}f[m]g_{N}[n-m]\&=sum _{m=0}^{n}f[m]g[n-m]+sum _{m=n+1}^{N-1}f[m]g[N+n-m]\[2pt]&=sum _{m=0}^{N-1}f[m]g[(n-m)_{bmod {N}}]\[2pt]&triangleq left(f*_{N}gright)[n]end{aligned}}}

()Eq.1)

La notación ( $f * N g$ ) para convolución cíclica denota convolución sobre el grupo cíclico de enteros módulo N.

La convolución circular surge con más frecuencia en el contexto de una convolución rápida con un algoritmo de transformada rápida de Fourier (FFT).

Algoritmos de convolución rápida

En muchas situaciones, las convoluciones discretas se pueden convertir en convoluciones circulares para que se puedan usar transformadas rápidas con una propiedad de convolución para implementar el cálculo. Por ejemplo, la convolución de secuencias de dígitos es la operación central en la multiplicación de números de varios dígitos, que por lo tanto se puede implementar de manera eficiente con técnicas de transformación (Knuth 1997, §4.3.3.C; von zur Gathen & Gerhard 2003, §8.2).

Eq.1 requiere $N$ operaciones aritméticas por valor de salida y $N 2$ operaciones para $N$ salidas. Eso se puede reducir significativamente con cualquiera de varios algoritmos rápidos. El procesamiento de señales digitales y otras aplicaciones suelen utilizar algoritmos de convolución rápidos para reducir el costo de la convolución a O( $N$ log $N$ ) complejidad.

Los algoritmos de convolución rápida más comunes utilizan algoritmos de transformada rápida de Fourier (FFT) a través del teorema de convolución circular. Específicamente, la convolución circular de dos secuencias de longitud finita se encuentra tomando una FFT de cada secuencia, multiplicándola por puntos y luego realizando una FFT inversa. Entonces, las convoluciones del tipo definido anteriormente se implementan eficientemente utilizando esa técnica junto con la extensión cero y/o el descarte de porciones de la salida. Otros algoritmos de convolución rápida, como el algoritmo de Schönhage-Strassen o la transformada de Mersenne, utilizan transformadas rápidas de Fourier en otros anillos.

Si una secuencia es mucho más larga que la otra, la extensión cero de la secuencia más corta y la convolución circular rápida no es el método computacionalmente más eficiente disponible. En cambio, descomponer la secuencia más larga en bloques y convolucionar cada bloque permite algoritmos más rápidos, como el método de superposición-guardar y el método de superposición-añadir. Un método de convolución híbrido que combina algoritmos de bloque y FIR permite una latencia de entrada-salida cero que es útil para los cálculos de convolución en tiempo real.

Dominio de definición

La convolución de dos funciones de valores complejos en $R d$ es en sí misma una función de valor complejo en $R d$ , definida por:

(f*g)(x)=int _{mathbf {R} ^{d}}f(y)g(x-y),dy=int _{mathbf {R} ^{d}}f(x-y)g(y),dy,

y está bien definido solo si $f$ y $g$ decae lo suficientemente rápido en el infinito para que exista la integral. Las condiciones para la existencia de la convolución pueden ser complicadas, ya que una explosión en $g$ en el infinito puede compensarse fácilmente con una velocidad lo suficientemente rápida. decaer en $f$ . Por lo tanto, la cuestión de la existencia puede implicar diferentes condiciones en $f$ y $g$ :

Funciones compatibles de forma compacta

Si $f$ y $g$ son funciones continuas de soporte compacto, entonces su convolución existe, y también es continua y de soporte compacto (Hörmander 1983, Capítulo 1). En términos más generales, si cualquiera de las funciones (por ejemplo, $f$ ) se admite de forma compacta y la otra se puede integrar localmente, entonces la convolución $f * g$ está bien definido y es continuo.

Convolución de $f$ y $g$ también está bien definido cuando ambas funciones son localmente integrables en cuadrado en $R$ y se admiten en un intervalo de la forma $[a, +\infty)$ (o ambos admitidos en $[-\infty, a]$ ).

Funciones integrables

La convolución de $f$ y $g$ existe si $f$ y $g$ son ambas funciones integrables de Lebesgue en L1(Rd), y en este caso $f * g$ también es integrable (Stein & Weiss 1971, Teorema 1.3). Esta es una consecuencia del teorema de Tonelli. Esto también es cierto para funciones en $L 1$ , bajo la convolución discreta, o más generalmente para la convolución en cualquier grupo.

Del mismo modo, si $f \in L 1$ ( $R d$ ) y $g \in L p$ ( $R d$ ) donde $1 \leq p \leq \infty$ , luego $f * g \in L p$ ( $R d$ ), y

{displaystyle |{f}*g|_{p}leq |f|_{1}|g|_{p}.}

En el caso particular $p = 1$ , esto muestra que $L 1$ es un álgebra de Banach bajo la convolución (y la igualdad de los dos lados se mantiene si $f$ y $g$ no son negativos en casi todas partes).

Más generalmente, la desigualdad de Young implica que la convolución es un mapa bilineal continuo entre $L p adecuados$ espacios. Específicamente, si $1 \leq p, q, r \leq \infty$ satisfacen:

{frac {1}{p}}+{frac {1}{q}}={frac {1}{r}}+1,

entonces

{displaystyle leftVert f*grightVert _{r}leq leftVert frightVert _{p}leftVert grightVert _{q},quad fin {mathcal {L}}^{p}, gin {mathcal {L}}^{q},}

para que la convolución sea un mapeo bilineal continuo de $L p \times L q$ a $L r$ . La desigualdad de Young para la convolución también es cierta en otros contextos (grupo circular, convolución en $Z$ ). La desigualdad anterior no es nítida en la línea real: cuando $1 < p, q, r < \infty$ , existe una constante $B p, q < 1$ tal que:

{displaystyle leftVert f*grightVert _{r}leq B_{p,q}leftVert frightVert _{p}leftVert grightVert _{q},quad fin {mathcal {L}}^{p}, gin {mathcal {L}}^{q}.}

El valor óptimo de $B p, q$ fue descubierto en 1975 e independientemente en 1976, véase Desigualdad de Brascamp-Lieb.

Una estimación más sólida es cierta siempre que $1 < p, q, r < \infty$ :

{displaystyle |f*g|_{r}leq C_{p,q}|f|_{p}|g|_{q,w}}

Donde $|g|_{q,w}$ es la débil norma Lq. Convolution también define un mapa continuo bilineal ${displaystyle L^{p,w}times L^{q,w}to L^{r,w}}$ para $<math alttext="{displaystyle 1<p,q,r1.p,q,r.JUEGO JUEGO {displaystyle 1 seg, q,r segùn <img alt="1<p,q,r$ , debido a la débil desigualdad joven:

{displaystyle |f*g|_{r,w}leq C_{p,q}|f|_{p,w}|g|_{r,w}.}

Funciones de decaimiento rápido

Además de las funciones compatibles de forma compacta y las funciones integrables, también se pueden convolucionar funciones que tienen un decaimiento lo suficientemente rápido en el infinito. Una característica importante de la convolución es que si tanto f como g decaen rápidamente, entonces f∗g también decae rápidamente. En particular, si f y g son funciones rápidamente decrecientes, entonces también lo es la convolución f∗g. Combinado con el hecho de que la convolución conmuta con la diferenciación (ver #Properties), se deduce que la clase de funciones de Schwartz está cerrada bajo convolución (Stein & Weiss 1971, Teorema 3.3).

Distribuciones

Bajo algunas circunstancias, es posible definir la convolución de una función con una distribución, o de dos distribuciones. Si f es una función compatible de forma compacta y g es una distribución, entonces f∗g es una función suave definida por una fórmula de distribución análoga a

int _{mathbf {R} ^{d}}{f}(y)g(x-y),dy.

Más generalmente, es posible extender la definición de la convolución de una manera única para que la ley asociativa

{displaystyle f*(g*varphi)=(f*g)*varphi }

sigue siendo válido en el caso de que f sea una distribución y g una distribución con soporte compacto (Hörmander 1983, §4.2).

Medidas

La revolución de cualquier dos medidas Borel μ y . de variación atada es la medida ${displaystyle mu *nu }$ definida por (Rudin 1962)

{displaystyle int _{mathbf {R} ^{d}}f(x),d(mu *nu)(x)=int _{mathbf {R} ^{d}}int _{mathbf {R} ^{d}}f(x+y),dmu (x),dnu (y).}

En particular,

{displaystyle (mu *nu)(A)=int _{mathbf {R} ^{d}times mathbf {R} ^{d}}1_{A}(x+y),d(mu times nu)(x,y),}

Donde ${displaystyle Asubset mathbf {R} ^{d}}$ es un conjunto mensurable y $1_{A}$ es la función indicadora de $A$ .

Esto concuerda con la convolución definida anteriormente cuando μ y ν se consideran distribuciones, así como con la convolución de las funciones L¹ cuando μ y ν son absolutamente continuas con respecto a la medida de Lebesgue.

La convolución de medidas también satisface la siguiente versión de la desigualdad de Young

{displaystyle |mu *nu |leq |mu ||nu |}

donde la norma es la variación total de una medida. Debido a que el espacio de medidas de variación acotada es un espacio de Banach, la convolución de medidas se puede tratar con métodos estándar de análisis funcional que pueden no aplicarse a la convolución de distribuciones.

Propiedades

Propiedades algebraicas

La convolución define un producto en el espacio lineal de funciones integrables. Este producto satisface las siguientes propiedades algebraicas, que formalmente significan que el espacio de funciones integrables con el producto dado por convolución es un álgebra asociativa conmutativa sin identidad (Strichartz 1994, §3.3). Otros espacios lineales de funciones, como el espacio de funciones continuas de soporte compacto, se cierran bajo la convolución, y así también forman álgebras asociativas conmutativas.

Commutativity: ${displaystyle f*g=g*f}$ Prueba: Por definición: ${displaystyle (f*g)(t)=int _{-infty }^{infty }f(tau)g(t-tau),dtau }$ Cambiar la variable de integración a ${displaystyle u=t-tau }$ el resultado sigue.
Associativity: ${displaystyle f*(g*h)=(f*g)*h}$ Prueba: Esto se deriva del uso del teorema de Fubini (es decir, las dobles integrales se pueden evaluar como integrales iterados en cualquier orden).
Distribución: ${displaystyle f*(g+h)=(f*g)+(f*h)}$ Prueba: Esto se deriva de la linealidad de la integral.
Asociatividad con multiplicación de escalar: ${displaystyle a(f*g)=(af)*g}$ para cualquier número real (o complejo) $a$ .
Identidad multiplicativa: Ningún álgebra de funciones posee una identidad para la convolución. La falta de identidad normalmente no es una molestia importante, ya que la mayoría de las colecciones de funciones en las que se realiza la convolución pueden convolverse con una distribución del delta (un impulso unitario, centrado en cero) o, por lo menos (como es el caso de la L¹) admitir aproximaciones a la identidad. Sin embargo, el espacio lineal de distribuciones compactas admite una identidad bajo la convolución. Específicamente, ${displaystyle f*delta =f}$ Donde δ es la distribución del delta.
Elemento inverso: Algunas distribuciones S tener un elemento inverso S⁻¹ para la convolución que entonces debe satisfacer ${displaystyle S^{-1}*S=delta }$ de la cual una fórmula explícita S⁻¹ se puede obtener.
El conjunto de distribuciones invertibles forma un grupo abeliano bajo la revolución.
Conjugación compleja: ${displaystyle {overline {f*g}}={overline {f}}*{overline {g}}}$
Relación con diferenciación: ${displaystyle (f*g)'=f'*g=f*g'}$ Prueba: ${displaystyle {begin{aligned}(f*g)'&={frac {d}{dt}}int _{-infty }^{infty }f(tau)g(t-tau),dtau \[4pt]&=int _{-infty }^{infty }f(tau){frac {partial }{partial t}}g(t-tau),dtau \[4pt]&=int _{-infty }^{infty }f(tau)g'(t-tau),dtau =f*g'.end{aligned}}}$
Relación con la integración: Si ${textstyle F(t)=int _{-infty }^{t}f(tau)dtau}$ y ${textstyle G(t)=int _{-infty }^{t}g(tau),dtau}$ entonces ${displaystyle (F*g)(t)=(f*G)(t)=int _{-infty }^{t}(f*g)(tau),dtau.}$

Integración

Si f y g son funciones integrables, entonces la integral de su convolución en todo el espacio se obtiene simplemente como el producto de sus integrales:

{displaystyle int _{mathbf {R} ^{d}}(f*g)(x),dx=left(int _{mathbf {R} ^{d}}f(x),dxright)left(int _{mathbf {R} ^{d}}g(x),dxright).}

Esto se deriva del teorema de Fubini. El mismo resultado se cumple si se asume que f y g son funciones medibles no negativas, según el teorema de Tonelli.

Diferenciación

En el caso de una variable,

{displaystyle {frac {d}{dx}}(f*g)={frac {df}{dx}}*g=f*{frac {dg}{dx}}}

donde d/dx es la derivada. Más generalmente, en el caso de funciones de varias variables, se cumple una fórmula análoga con la derivada parcial:

{frac {partial }{partial x_{i}}}(f*g)={frac {partial f}{partial x_{i}}}*g=f*{frac {partial g}{partial x_{i}}}.

Una consecuencia particular de esto es que la convolución puede verse como un "suavizado" operación: la convolución de f y g es diferenciable tantas veces como f y g lo sean en total.

Estas identidades se cumplen bajo la condición precisa de que f y g son absolutamente integrables y al menos una de ellas tiene un absolutamente integrable (L¹) derivada débil, como consecuencia de la desigualdad de convolución de Young. Por ejemplo, cuando f es continuamente diferenciable con soporte compacto, y g es una función localmente integrable arbitraria,

{displaystyle {frac {d}{dx}}(f*g)={frac {df}{dx}}*g.}

Estas identidades también se mantienen mucho más ampliamente en el sentido de distribuciones moderadas si una de f o g es una distribución templada rápidamente decreciente, una una distribución temperada con soporte compacto o una función de Schwartz y la otra es una distribución temperada. Por otro lado, dos funciones positivas integrables e infinitamente diferenciables pueden tener una convolución continua en ninguna parte.

En el caso discreto, el operador diferencia D f(n) = f( n + 1) − f(n) satisface una relación análoga:

{displaystyle D(f*g)=(Df)*g=f*(Dg).}

Teorema de convolución

El teorema de la convolución establece que

{mathcal {F}}{f*g}=kcdot {mathcal {F}}{f}cdot {mathcal {F}}{g}

Donde ${displaystyle {mathcal {F}}{f}}$ denota la transformación de Fourier $f$ , y $k$ es una constante que depende de la normalización específica de la transformación Fourier. Versiones de este teorema también sostienen para la transformación de Laplace, la transformación de dos lados, Z-transform y Mellin transformar.

Por otro lado, si ${displaystyle {mathcal {W}}}$ es la matriz de transformación de Fourier, entonces

{displaystyle {mathcal {W}}left(C^{(1)}xast C^{(2)}yright)=left({mathcal {W}}C^{(1)}bullet {mathcal {W}}C^{(2)}right)(xotimes y)={mathcal {W}}C^{(1)}xcirc {mathcal {W}}C^{(2)}y}

Donde ${displaystyle bullet }$ es producto que multiplica la cara, $otimes$ denota producto Kronecker, $circ$ denota producto Hadamard (este resultado es una evolución de las propiedades del conteo).

Equivarianza traslacional

La convolución conmuta con las traslaciones, lo que significa que

{displaystyle tau _{x}(f*g)=(tau _{x}f)*g=f*(tau _{x}g)}

donde τ_xf es la traducción de la función f por x definida por

{displaystyle (tau _{x}f)(y)=f(y-x).}

Si f es una función de Schwartz, entonces τ_xf es la convolución con una función delta de Dirac traducida τ_xf = f ∗ τ_x δ. Entonces, la invariancia de traducción de la convolución de las funciones de Schwartz es una consecuencia de la asociatividad de la convolución.

Además, bajo ciertas condiciones, la convolución es la operación invariante de traducción más general. Informalmente hablando, lo siguiente es válido

Supongamos que S es un operador lineal vinculado que actúa en funciones que se comunica con traducciones: S()τ_xf) τ_x()Sf) para todos x. Entonces... S se da como convolución con una función (o distribución) g_S; eso es Sf = g_S Alternativa f.

Por lo tanto, algunas operaciones invariantes de traducción se pueden representar como convolución. Las convoluciones juegan un papel importante en el estudio de sistemas invariantes en el tiempo, y especialmente en la teoría de sistemas LTI. La función de representación g_S es la respuesta al impulso de la transformación S.

Una versión más precisa del teorema citado anteriormente requiere especificar la clase de funciones sobre las que se define la convolución, y también requiere asumir además que S debe ser un operador lineal continuo con respecto a la topología apropiada. Se sabe, por ejemplo, que todo operador lineal continuo invariante de traslación continua sobre L¹ es la convolución con una medida Borel finita. Más generalmente, cada operador lineal continuo invariable de traducción continua en L^p para 1 ≤ p < ∞ es la convolución con una distribución temperada cuya transformada de Fourier está acotada. A saber, todos están dados por multiplicadores de Fourier acotados.

Convoluciones en grupos

Si G es un grupo adecuado dotado de una medida λ, y si f y g son funciones integrables reales o de valor complejo en G, entonces podemos definir su convolución por

{displaystyle (f*g)(x)=int _{G}f(y)gleft(y^{-1}xright),dlambda (y).}

No es conmutativo en general. En casos típicos de interés G es un grupo topológico Hausdorff localmente compacto y λ es una medida (izquierda-). En ese caso, a menos que G es unimodular, la convolución definida de esta manera no es la misma ${textstyle int fleft(xy^{-1}right)g(y),dlambda (y)}$ . La preferencia de uno sobre el otro se hace para que la convolución con una función fija g comunicaciones con traducción izquierda en el grupo:

{displaystyle L_{h}(f*g)=(L_{h}f)*g.}

Además, la convención también es necesaria para mantener la coherencia con la definición de la convolución de medidas que se proporciona a continuación. Sin embargo, con una medida de Haar derecha en lugar de izquierda, se prefiere la última integral sobre la primera.

En grupos abelianos localmente compactos, se cumple una versión del teorema de convolución: la transformada de Fourier de una convolución es el producto puntual de las transformadas de Fourier. El grupo circular T con la medida de Lebesgue es un ejemplo inmediato. Para una g fija en L¹(T), tenemos el siguiente operador familiar que actúa en el espacio de Hilbert L²(T):

{displaystyle T{f}(x)={frac {1}{2pi }}int _{mathbf {T} }{f}(y)g(x-y),dy.}

El operador T es compacto. Un cálculo directo muestra que su adjunto T* es convolución con

{displaystyle {bar {g}}(-y).}

Por la propiedad de conmutatividad citada arriba, T es normal: T* T = TT*. Además, T viaja con los operadores de traducción. Considere la familia S de operadores que consta de todas esas convoluciones y los operadores de traducción. Entonces S es una familia itinerante de operadores normales. Según la teoría espectral, existe una base ortonormal {h_k} que diagonaliza simultáneamente S. Esto caracteriza las circunvoluciones en el círculo. Específicamente, tenemos

h_{k}(x)=e^{ikx},quad kin mathbb {Z};

que son precisamente los personajes de T. Cada convolución es un operador de multiplicación compacto en esta base. Esto puede verse como una versión del teorema de convolución discutido anteriormente.

Un ejemplo discreto es un grupo cíclico finito de orden n. Los operadores de convolución están representados aquí por matrices circulantes y pueden ser diagonalizados por la transformada discreta de Fourier.

Un resultado similar es válido para grupos compactos (no necesariamente abelianos): los coeficientes de matriz de representaciones unitarias de dimensión finita forman una base ortonormal en L² por Peter– El teorema de Weyl y un análogo del teorema de convolución siguen siendo válidos, junto con muchos otros aspectos del análisis armónico que dependen de la transformada de Fourier.

Convolución de medidas

Sea G un grupo topológico (escrito multiplicativamente). Si μ y ν son medidas de Borel finitas en G, entonces su convolución μ∗ν se define como la medida de avance de la acción de grupo y puede escribirse como

{displaystyle (mu *nu)(E)=iint 1_{E}(x+y),dmu (x),dnu (y)}

para cada subconjunto medible E de G. La convolución es también una medida finita, cuya variación total satisface

{displaystyle |mu *nu |leq left|mu right|left|nu right|.}

En el caso de que G sea localmente compacto con la medida de Haar (izquierda) λ, y μ y ν sean absolutamente continuos con respecto a λ, de modo que cada uno tenga una función de densidad, entonces el la convolución μ∗ν también es absolutamente continua, y su función de densidad es solo la convolución de las dos funciones de densidad separadas.

Si μ y ν son medidas de probabilidad en el grupo topológico (R,+), entonces la convolución μ ∗ν es la distribución de probabilidad de la suma X + Y de dos variables aleatorias independientes X y Y cuyas distribuciones respectivas son μ y ν.

Convolución íntima

En el análisis convexo, el infimal convolution (no idéntico) $+infty$ ) funciones convex ${displaystyle f_{1},dotsf_{m}}$ on $mathbb {R} ^{n}$ se define por:

{displaystyle (f_{1}*cdots *f_{m})(x)=inf _{x}{f_{1}(x_{1})+cdots +f_{m}(x_{m})|x_{1}+cdots +x_{m}=x}.}

{displaystyle varphi ^{*}(x)=sup _{y}(xcdot y-varphi (y)).}

{displaystyle (f_{1}*cdots *f_{m})^{*}(x)=f_{1}^{*}(x)+cdots +f_{m}^{*}(x).}

Biálgebras

Sea (X, Δ, ∇, ε, η) una biálgebra con comultiplicación Δ, multiplicación ∇, unidad η y país ε. La convolución es un producto definido en el álgebra de endomorfismo End(X) como sigue. Sea φ, ψ ∈ End(X), es decir, φ, ψ: X → X son funciones que respetan toda la estructura algebraica de X, entonces la convolución φ∗ψ se define como la composición

{displaystyle Xmathrel {xrightarrow {Delta } } Xotimes Xmathrel {xrightarrow {phi otimes psi } } Xotimes Xmathrel {xrightarrow {nabla } } X.}

La convolución aparece notablemente en la definición de álgebras de Hopf (Kassel 1995, §III.3). Una biálgebra es un álgebra de Hopf si y solo si tiene una antípoda: un endomorfismo S tal que

S*operatorname {id} _{X}=operatorname {id} _{X}*S=eta circ varepsilon.

Aplicaciones

El borrón gausiano se puede utilizar para obtener una imagen digital lisa a escala de grises de una impresión de medio tono.

La convolución y las operaciones relacionadas se encuentran en muchas aplicaciones en ciencias, ingeniería y matemáticas.

En procesamiento de imágenes
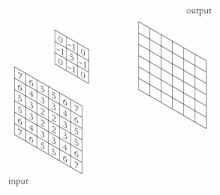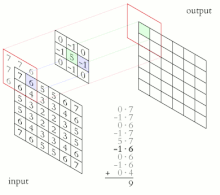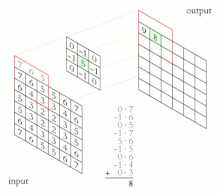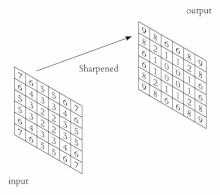
- En el procesamiento digital de imágenes, el filtrado conversor juega un papel importante en muchos algoritmos importantes en la detección de bordes y procesos relacionados (ver kernel (procesamiento de imagen))
- En la óptica, una fotografía fuera de foco es una evolución de la imagen aguda con una función de lente. El término fotográfico para esto es bokeh.
- En aplicaciones de procesamiento de imágenes, como añadir borroso.
En procesamiento digital de datos
- En la química analítica, los filtros de suavizado Savitzky–Golay se utilizan para el análisis de datos espectroscópicos. Pueden mejorar la relación entre señal y ruido con una mínima distorsión del espectro
- En las estadísticas, un promedio de movimiento ponderado es una convolución.
En la acústica, la reverberación es la convolución del sonido original con ecos de objetos que rodean la fuente de sonido.
- En el procesamiento digital de señales, la convolución se utiliza para mapear la respuesta de impulso de una sala real en una señal de audio digital.
- En la convolución electrónica de la música es la imposición de una estructura espectral o rítmica sobre un sonido. A menudo este sobre o estructura se toma de otro sonido. La convolución de dos señales es el filtrado de uno a otro.
En la ingeniería eléctrica, la convolución de una función (la señal de entrada) con una segunda función (la respuesta de impulso) da la salida de un sistema lineal de tiempo invariante (LTI). En cualquier momento dado, la salida es un efecto acumulado de todos los valores anteriores de la función de entrada, con los valores más recientes que suelen tener la mayor influencia (expresado como factor multiplicador). La función de respuesta del impulso proporciona ese factor como función del tiempo transcurrido desde que se produjo cada valor de entrada.
En física, donde haya un sistema lineal con un "principio de superposición", una operación de convolución hace una aparición. Por ejemplo, en la línea de espectroscopia ampliando debido al efecto Doppler por su cuenta da una forma espectral de Gaussian y la colisión ampliando solo da una forma de línea Lorentziana. Cuando ambos efectos son operativos, la forma de línea es una convolución de Gaussian y Lorentzian, una función Voigt.
- En la espectroscopia de fluorescencia resolvida por el tiempo, la señal de excitación se puede tratar como una cadena de pulsos delta, y la fluorescencia medida es una suma de decaimientos exponenciales de cada pulso delta.
- En la dinámica de fluidos computacionales, el modelo de turbulencia grande de simulación de eddy (LES) utiliza la operación convolution para reducir la gama de escalas de longitud necesarias en la computación reduciendo así el coste computacional.
En teoría de probabilidad, la distribución de probabilidad de la suma de dos variables aleatorias independientes es la convolución de sus distribuciones individuales.
- En la estimación de la densidad del núcleo, se calcula una distribución de puntos de muestra por convolución con un núcleo, como un Gaussiano isotrópico.
En sistemas de planificación de tratamientos de radioterapia, la mayoría de los códigos de cálculo modernos aplica un algoritmo de superposición-convolution.
En la fiabilidad estructural, el índice de fiabilidad se puede definir sobre la base del teorema de la convolución.
- La definición de índice de fiabilidad para funciones estatales límite con distribuciones no normales se puede establecer correspondiente a la función de distribución conjunta. De hecho, la función de distribución conjunta se puede obtener utilizando la teoría de la convolución.
Redes neuronales revolucionarias aplican múltiples cascadas convolution kernels con aplicaciones en visión de máquina e inteligencia artificial. Aunque estos son en realidad cross-correlations en lugar de convoluciones en la mayoría de los casos.
En la hidrodinámica de partículas de Smoothed, se calculan simulaciones de dinámicas de fluido utilizando partículas, cada una con núcleos circundantes. Para cualquier partícula dada $i$ , alguna cantidad física $A_{i}$ se calcula como una convolución de $A_{j}$ con una función de ponderación, donde $j$ denota a los vecinos de la partícula $i$ : aquellos que se encuentran dentro de su núcleo. La convolución se aproxima como una suma sobre cada vecino.

Contenido relacionado

Más resultados...