Círculos de Apolonio

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Varios conjuntos de círculos asociados con Apolonio de Perga

Los círculos de Apolonio son cualquiera de varios conjuntos de círculos asociados con Apolonio de Perga, un renombrado geómetra griego. La mayoría de estos círculos se encuentran en la geometría euclidiana plana, pero se han definido análogos en otras superficies; por ejemplo, las contrapartes en la superficie de una esfera se pueden definir mediante proyección estereográfica.

Los usos principales de este término son cinco:

Apollonius mostró que un círculo se puede definir como el conjunto de puntos en un plano que tiene un especificado ratio de distancias a dos puntos fijos, conocidos como foci. Esto Apollonian circle es la base del problema de búsqueda de Apolonio. Es un caso particular de la primera familia descrita en #2.
El Círculos de Apolonio son dos familias de círculos ortogonales mutuamente. La primera familia consiste en los círculos con todas las proporciones de distancia posibles a dos focos fijos (los mismos círculos que en #1), mientras que la segunda familia consiste en todos los círculos posibles que pasan a través de ambos focos. Estos círculos forman la base de coordenadas bipolares.
El círculos de Apolonio de un triángulo son tres círculos, cada uno de los cuales pasa a través de un vértice del triángulo y mantiene una relación constante de distancias a los otros dos. Los puntos isodinámicos y la línea Lemoine de un triángulo se pueden resolver utilizando estos círculos de Apolonio.
Problema de Apolonio es construir círculos que son simultáneamente tangentes a tres círculos especificados. Las soluciones a este problema se llaman a veces círculos de Apolonio.
El Gasto Apolonio—uno de los primeros fractales descritos— es un conjunto de círculos mutuamente tangentes, formado por resolver el problema de Apolonio iterativamente.

Apolonio' definición de círculo

Un círculo generalmente se define como el conjunto de puntos P a una distancia dada r (el radio del círculo) desde un punto dado (el círculo' 39;centro). Sin embargo, existen otras definiciones equivalentes de círculo. Apolonio descubrió que un círculo podría definirse como el conjunto de puntos P que tienen una proporción de distancias k = d₁/d₂ a dos puntos dados (etiquetados A y B en la Figura 1). Estos dos puntos a veces se denominan focos.

Demostración utilizando vectores en espacios euclidianos

Sean d₁, d₂ números reales positivos no iguales. Sea C el punto de división interna de AB en la relación d₁: d₂ y D el punto de división externo de AB en la misma proporción, d₁: d₂.

{displaystyle {overrightarrow {mathrm {PC} }}={frac {d_{2}{overrightarrow {mathrm {PA} }}+d_{1}{overrightarrow {mathrm {PB} }}}{d_{2}+d_{1}}}, {overrightarrow {mathrm {PD} }}={frac {d_{2}{overrightarrow {mathrm {PA} }}-d_{1}{overrightarrow {mathrm {PB} }}}{d_{2}-d_{1}}}.}

Entonces,

{displaystyle {begin{aligned}&mathrm {PA}:mathrm {PB} =d_{1}:d_{2}.\Leftrightarrow {}&d_{2}|{overrightarrow {mathrm {PA} }}|=d_{1}|{overrightarrow {mathrm {PB} }}|.\Leftrightarrow {}&d_{2}^{2}|{overrightarrow {mathrm {PA} }}|^{2}=d_{1}^{2}|{overrightarrow {mathrm {PB} }}|^{2}.\Leftrightarrow {}&(d_{2}{overrightarrow {mathrm {PA} }}+d_{1}{overrightarrow {mathrm {PB} }})cdot (d_{2}{overrightarrow {mathrm {PA} }}-d_{1}{overrightarrow {mathrm {PB} }})=0.\Leftrightarrow {}&{frac {d_{2}{overrightarrow {mathrm {PA} }}+d_{1}{overrightarrow {mathrm {PB} }}}{d_{2}+d_{1}}}cdot {frac {d_{2}{overrightarrow {mathrm {PA} }}-d_{1}{overrightarrow {mathrm {PB} }}}{d_{2}-d_{1}}}=0.\Leftrightarrow {}&{overrightarrow {mathrm {PC} }}cdot {overrightarrow {mathrm {PD} }}=0.\Leftrightarrow {}&{overrightarrow {mathrm {PC} }}={vec {0}}vee {overrightarrow {mathrm {PD} }}={vec {0}}vee {overrightarrow {mathrm {PC} }}perp {overrightarrow {mathrm {PD} }}.\Leftrightarrow {}&mathrm {P} =mathrm {C} vee mathrm {P} =mathrm {D} vee angle {mathrm {CPD} }=90^{circ }.end{aligned}}}

Por lo tanto, el punto P está en el círculo que tiene el diámetro CD.

Demostración utilizando el teorema de la bisectriz del ángulo

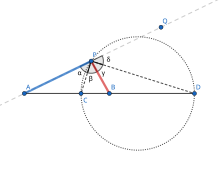
Primera consideración el punto ${displaystyle C}$ en el segmento de línea entre ${displaystyle A}$ y ${displaystyle B}$ , satisfaciendo la relación. Por definición

{displaystyle {frac {|AP|}{|BP|}}={frac {|AC|}{|BC|}}}

{displaystyle alpha =angle APC}

{displaystyle beta =angle CPB}

Siguiente tomar el otro punto ${displaystyle D}$ en la línea extendida ${displaystyle AB}$ que satisface la relación. Así que...

{displaystyle {frac {|AP|}{|BP|}}={frac {|AD|}{|BD|}}.}

{displaystyle Q}

{displaystyle AP}

{displaystyle PD}

{displaystyle angle QPB}

{displaystyle gamma =angle BPD}

{displaystyle delta =angle QPD}

{displaystyle beta +gamma =90^{circ }}

{displaystyle P}

{displaystyle CD}

Problema de persecución de Apolonio

El problema de persecución de Apolonio consiste en encontrar si un barco que sale de un punto A con una velocidad v_A interceptará a otro barco que sale de un punto diferente B a velocidad v_B. El tiempo mínimo en la interceptación de los dos barcos se calcula mediante trayectorias en línea recta. Si los barcos' las velocidades se mantienen constantes, su relación de velocidad está definida por μ. Si ambos barcos chocan o se encuentran en un punto futuro, I, entonces las distancias de cada uno están relacionadas por la ecuación:

{displaystyle a=mu b}

Cuadrando ambos lados, obtenemos:

{displaystyle a^{2}=b^{2}mu ^{2}}

{displaystyle a^{2}=x^{2}+y^{2}}

{displaystyle b^{2}=(d-x)^{2}+y^{2}}

{displaystyle x^{2}+y^{2}=[(d-x)^{2}+y^{2}]mu ^{2}}

Expandiendo:

{displaystyle x^{2}+y^{2}=[d^{2}+x^{2}-2dx+y^{2}]mu ^{2}}

Mayor expansión:

{displaystyle x^{2}+y^{2}=x^{2}mu ^{2}+y^{2}mu ^{2}+d^{2}mu ^{2}-2dxmu ^{2}}

Trayendo al lado izquierdo:

{displaystyle x^{2}-x^{2}mu ^{2}+y^{2}-y^{2}mu ^{2}-d^{2}mu ^{2}+2dxmu ^{2}=0}

Factorización:

{displaystyle x^{2}(1-mu ^{2})+y^{2}(1-mu ^{2})-d^{2}mu ^{2}+2dxmu ^{2}=0}

Dividiendo por ${displaystyle 1-mu ^{2}}$ :

{displaystyle x^{2}+y^{2}-{frac {d^{2}mu ^{2}}{1-mu ^{2}}}+{frac {2dxmu ^{2}}{1-mu ^{2}}}=0}

Completando el cuadrado:

{displaystyle left(x+{frac {dmu ^{2}}{1-mu ^{2}}}right)^{2}-{frac {d^{2}mu ^{4}}{(1-mu ^{2})^{2}}}-{frac {d^{2}mu ^{2}}{1-mu ^{2}}}+y^{2}=0}

Trae los términos no cuadrados al lado derecho:

{displaystyle {begin{aligned}left(x+{frac {dmu ^{2}}{1-mu ^{2}}}right)^{2}+y^{2}&={frac {d^{2}mu ^{4}}{(1-mu ^{2})^{2}}}+{frac {d^{2}mu ^{2}}{1-mu ^{2}}}\&={frac {d^{2}mu ^{4}}{(1-mu ^{2})^{2}}}+{frac {d^{2}mu ^{2}}{1-mu ^{2}}}{frac {(1-mu ^{2})}{(1-mu ^{2})}}\&={frac {d^{2}mu ^{4}+d^{2}mu ^{2}-d^{2}mu ^{4}}{(1-mu ^{2})^{2}}}\&={frac {d^{2}mu ^{2}}{(1-mu ^{2})^{2}}}end{aligned}}}

Entonces:

{displaystyle left(x+{frac {dmu ^{2}}{1-mu ^{2}}}right)^{2}+y^{2}=left({frac {dmu }{1-mu ^{2}}}right)^{2}}

Por lo tanto, el punto debe estar en un círculo definido por Apolonio, con sus puntos de partida como focos.

Círculos que comparten un eje radical

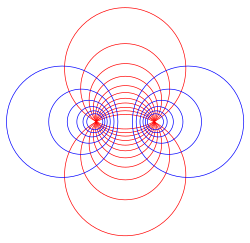
Los círculos definidos por el problema de búsqueda Apolonio para los mismos dos puntos A y B, pero con diferentes proporciones de las dos velocidades, se descomponen entre sí y forman una familia continua que cubre todo el plano; esta familia de círculos se conoce como una lápiz hiperbólico. Otra familia de círculos, los círculos que pasan por ambos A y B, también se llaman un lápiz, o más específicamente un lápiz elíptico. Estos dos lápices de los círculos Apolonios se intersecten en ángulos rectos y forman la base del sistema de coordenadas bipolar. Dentro de cada lápiz, los dos círculos tienen el mismo eje radical; los dos ejes radicales de los dos lápices son perpendiculares, y los centros de los círculos de un lápice se encuentran en el eje radical del otro lápiz.

Soluciones para Apolonio' problema

El problema de Apolonio puede tener hasta ocho soluciones. Los tres círculos dados se muestran en negro, mientras que los círculos de solución son coloreados.

En la geometría plana euclidiana, el problema de Apolonio es construir círculos que sean tangentes a tres círculos dados en un plano.

Tres círculos dados generalmente tienen ocho círculos diferentes que son tangentes a ellos y cada círculo solución encierra o excluye los tres círculos dados de una manera diferente: en cada solución, se incluye un subconjunto diferente de los tres círculos.

Junta apolínea

Al resolver el problema de Apolonio' problema repetidamente para encontrar el círculo inscrito, los intersticios entre círculos mutuamente tangenciales se pueden llenar con una finura arbitraria, formando una junta apolínea, también conocida como empaquetadura de Leibniz o empaquetadura apolínea. Esta junta es un fractal, es autosimilar y tiene una dimensión d que no se conoce exactamente pero que es aproximadamente 1,3, que es mayor que la de una curva regular (o rectificable) (d = 1) pero menor que la de un avión (d = 2). La junta apolínea fue descrita por primera vez por Gottfried Leibniz en el siglo XVII y es un precursor curvo del triángulo de Sierpiński del siglo XX. La junta apolínea también tiene conexiones profundas con otros campos de las matemáticas; por ejemplo, es el conjunto límite de grupos kleinianos; consulte también el teorema del embalaje circular.

Puntos isodinámicos de un triángulo

El círculos de Apolonio puede también denotar tres círculos especiales ${displaystyle {mathcal {C}}_{1},{mathcal {C}}_{2},{mathcal {C}}_{3}}$ definido por un triángulo arbitrario ${displaystyle mathrm {A_{1}A_{2}A_{3}} }$ . El círculo ${displaystyle {mathcal {C}}_{1}}$ se define como el círculo único que pasa por el triángulo vértice ${displaystyle mathrm {A_{1}} }$ que mantiene una relación constante de distancias a los otros dos vértices ${displaystyle mathrm {A_{2}} }$ y ${displaystyle mathrm {A_{3}} }$ (cf. Apolonio' definición del círculo anterior). Del mismo modo, el círculo ${displaystyle {mathcal {C}}_{2}}$ se define como el círculo único que pasa por el triángulo vértice ${displaystyle mathrm {A_{2}} }$ que mantiene una relación constante de distancias a los otros dos vértices ${displaystyle mathrm {A_{1}} }$ y ${displaystyle mathrm {A_{3}} }$ , y así sucesivamente para el círculo ${displaystyle {mathcal {C}}_{3}}$ .

Los tres círculos intersectan el círculo del triángulo ortogonalmente. Los tres círculos pasan por dos puntos, que son conocidos como puntos isodinámicos ${displaystyle S}$ y ${displaystyle S^{prime }}$ del triángulo. La línea que conecta estos puntos comunes de intersección es el eje radical para los tres círculos. Los dos puntos isodinámicos son inversos unos de otros relativos al círculo del triángulo.

Los centros de estos tres círculos caen en una sola línea (la línea de Lemoine). Esta recta es perpendicular al eje radical, que es la recta determinada por los puntos isodinámicos.

Más resultados...