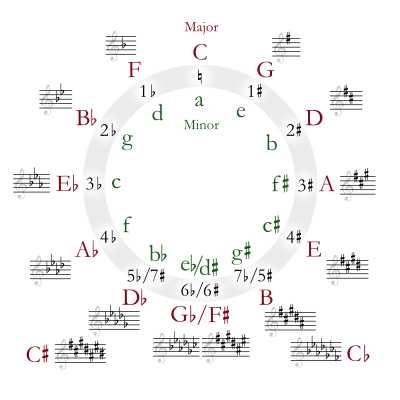
Circulo de quintas
En teoría musical, el círculo de quintas es una forma de organizar los 12 tonos cromáticos como una secuencia de quintas perfectas. (Esto es estrictamente cierto en el sistema estándar de temperamento igual de 12 tonos: el uso de un sistema diferente requiere que un intervalo de sexta disminuida se trate como una quinta). Si se elige C como punto de partida, la secuencia es: C, G, D, A, E, B (=C♭), F♯ (=G♭), C♯ (=D♭), A♭, E ♭, B♭, F. Continuar el patrón desde F devuelve la secuencia a su punto inicial de C. Este orden coloca las firmas de clave más estrechamente relacionadas entre sí. Por lo general, se ilustra en forma de círculo.
Definición
El círculo de quintas organiza tonos en una secuencia de quintas justas, generalmente mostrada como un círculo con los tonos (y sus correspondientes tonalidades) en una progresión en el sentido de las agujas del reloj. Los músicos y compositores suelen utilizar el círculo de quintas para describir las relaciones musicales entre tonos. Su diseño es útil para componer y armonizar melodías, construir acordes y modular a diferentes tonos dentro de una composición.
Usando el sistema de entonación justa, una quinta perfecta consta de dos tonos con una relación de frecuencia de 3:2, pero generar doce quintas perfectas sucesivas de esta manera no da como resultado un regreso a la clase de tono de la nota inicial. Para ajustar esto, los instrumentos generalmente se afinan con el sistema de temperamento igual. Doce quintas de igual temperamento conducen a una nota exactamente siete octavas por encima del tono inicial; esto da como resultado una quinta perfecta que equivale a siete semitonos de igual temperamento.
La parte superior del círculo muestra la tonalidad de do mayor, sin sostenidos ni bemoles. Procediendo en el sentido de las agujas del reloj, los tonos ascienden por quintas. Las armaduras de clave asociadas con esos tonos también cambian: la clave de G tiene un sostenido, la clave de D tiene 2 sostenidos, y así sucesivamente. De manera similar, procediendo en sentido contrario a las agujas del reloj desde la parte superior del círculo, las notas cambian por quintas descendentes y las armaduras de clave cambian en consecuencia: la clave de F tiene un bemol, la clave de B♭ tiene 2 bemoles, y así sucesivamente. Algunas teclas (en la parte inferior del círculo) se pueden escribir en sostenidos o bemoles.
Comenzar en cualquier tono y ascender en una quinta genera los doce tonos antes de volver a la clase de tono inicial (una clase de tono consta de todas las notas indicadas por una letra determinada, independientemente de la octava, todas "C"s, por ejemplo, pertenecen a la misma clase de tono). Moviéndose en el sentido contrario a las agujas del reloj, los tonos descienden una quinta, pero ascender una cuarta perfecta conducirá a la misma nota una octava más alta (por lo tanto, en la misma clase de tono). Moverse en sentido contrario a las agujas del reloj desde C podría considerarse como descender una quinta a F, o ascender una cuarta a F.
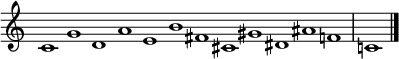 Círculo de cinco agujas del reloj en una octava | 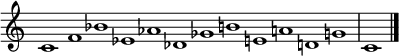 Círculo de las quintas en sentido contrario en una octava |
Estructura y uso
Armas de clave diatónicas
Cada uno de los doce tonos puede servir como tónica de una tonalidad mayor o menor, y cada una de estas tonalidades tendrá asociada una escala diatónica. El diagrama circular muestra el número de sostenidos o bemoles en cada firma de clave, con la clave mayor indicada por una letra mayúscula y la clave menor indicada por una letra minúscula. Las claves mayores y menores que tienen la misma firma de clave se denominan mayor relativo y menor relativo entre sí.
Modulación y progresión de acordes
La música tonal a menudo se modula a un nuevo centro tonal cuya firma clave difiere del original en solo un bemol o un sostenido. Estas claves estrechamente relacionadas están separadas por una quinta entre sí y, por lo tanto, son adyacentes en el círculo de quintas. Las progresiones de acordes también suelen moverse entre acordes cuyas raíces están relacionadas por una quinta justa, lo que hace que el círculo de quintas sea útil para ilustrar la "distancia armónica" entre acordes.
El círculo de quintas se utiliza para organizar y describir la función armónica de los acordes. Los acordes pueden progresar en un patrón de cuartas perfectas ascendentes (alternativamente vistas como quintas perfectas descendentes) en "sucesión funcional". Esto se puede mostrar "...por el círculo de quintas (en el que, por lo tanto, el grado de escala II está más cerca de la dominante que el grado de escala IV)". Desde este punto de vista, la tónica se considera el punto final de una progresión de acordes derivada del círculo de quintas.
Según Harmony in Western Music de Richard Franko Goldman, "el acorde IV está, en los mecanismos más simples de las relaciones diatónicas, a la mayor distancia del I. En términos del círculo [descendente] de quintas, conduce lejos de I, en lugar de hacia él." Afirma que la progresión I–ii–V–I (una cadencia auténtica) se sentiría más final o resuelta que I–IV–I (una cadencia plagal). Goldman está de acuerdo con Nattiez, quien argumenta que "el acorde en el cuarto grado aparece mucho antes que el acorde en II, y el posterior I final, en la progresión I–IV–viio–iii –vi–ii–V–I", y allí también está más lejos de la tónica. (En este artículo y otros relacionados, los números romanos en mayúsculas indican tríadas principales, mientras que los números romanos en minúsculas indican tríadas menores).
Cierre de círculo en sistemas de afinación desiguales
Usar la proporción exacta de frecuencias de 3:2 para definir una quinta perfecta (solo entonación) no da como resultado un regreso a la clase de tono de la nota inicial después de recorrer el círculo de quintas. La afinación de temperamento igual produce quintas que vuelven a un tono exactamente siete octavas por encima del tono inicial y hace que la relación de frecuencia de cada semitono sea la misma. Una quinta con el mismo temperamento tiene una relación de frecuencia de 27/12:1 (o alrededor de 1,498307077:1), aproximadamente dos centésimas más estrecha que una quinta justamente afinada con una relación de 3:2.
Al ascender por quintas afinadas correctamente no se cierra el círculo por un exceso de aproximadamente 23,46 centésimas, aproximadamente un cuarto de semitono, un intervalo conocido como la coma pitagórica. En la afinación pitagórica, este problema se resuelve acortando notablemente el ancho de uno de los doce quintos, lo que lo hace severamente disonante. Esta quinta anómala se llama la quinta del lobo, una referencia humorística a un lobo que aúlla una nota fuera de tono. El sistema de afinación de medio tono de cuarto de coma utiliza once quintas ligeramente más estrechas que la quinta igualmente temperada, y requiere una quinta de lobo mucho más ancha e incluso más disonante para cerrar el círculo. Los sistemas de afinación más complejos basados en la entonación justa, como la afinación de 5 límites, usan como máximo ocho quintas afinadas justamente y al menos tres quintas no justas (algunas un poco más estrechas y otras un poco más anchas que la quinta justa) para cerrar el círculo. Otros sistemas de afinación utilizan hasta 53 tonos (los 12 tonos originales y 42 más entre ellos) para cerrar el círculo de quintas.
Historia
El círculo de quintas se desarrolló a finales de 1600 y principios de 1700 para teorizar la modulación de la época barroca (ver § Era barroca).
El primer diagrama del círculo de quintas aparece en la Grammatika (1677) del compositor y teórico Nikolay Diletsky, quien pretendía presentar la teoría musical como una herramienta para la composición. Fue "el primero de su tipo, destinado a enseñar a una audiencia rusa cómo escribir composiciones polifónicas al estilo occidental".
El compositor y teórico alemán Johann David Heinichen creó de forma independiente un diagrama de círculo de quintas en su obra Neu erfundene und gründliche Anweisung (1711), a la que llamó "Círculo musical" (Alemán: Musicalischer Circul). Esto también se publicó en su Der General-Bass in der Composition (1728).
Heinichen colocó la tonalidad menor relativa junto a la tonalidad mayor, lo que no reflejaba la proximidad real de las tonalidades. Johann Mattheson (1735) y otros intentaron mejorar esto: David Kellner (1737) propuso tener las tonalidades mayores en un círculo y las tonalidades menores relativas en un segundo círculo interior. Esto se desarrolló más tarde en el espacio cordal, incorporando también el paralelo menor.
Algunas fuentes dan a entender que el círculo de quintas era conocido en la antigüedad, por Pitágoras. Esto es un malentendido y un anacronismo. La afinación por quintas (llamada afinación pitagórica) data de la antigua Mesopotamia; ver Música de Mesopotamia § Teoría de la música, aunque no extendieron esto a una escala de doce notas, deteniéndose en siete. La coma pitagórica fue calculada por Euclides y por matemáticos chinos (en el Huainanzi); véase la coma pitagórica § Historia. Así, en la antigüedad se sabía que un ciclo de doce quintas era casi exactamente siete octavas (más prácticamente, la alternancia de quintas ascendentes y cuartas descendentes era casi exactamente una octava). Sin embargo, este era un conocimiento teórico y no se usaba para construir una escala de doce tonos repetitiva, ni para modular. Esto se hizo más tarde en el temperamento de tono medio y el temperamento igual de doce tonos, que permitía la modulación sin dejar de estar afinado, pero no se desarrolló en Europa hasta alrededor de 1500.
Usar
En las piezas musicales de la era de la música barroca y la era de la música clásica y en la música popular occidental, la música tradicional y la música folclórica, cuando las piezas o canciones se modulan a una nueva tonalidad, estas modulaciones a menudo se asocian con el círculo de quintas.
En la práctica, las composiciones rara vez utilizan todo el círculo de quintas. Más comúnmente, los compositores hacen uso de "la idea compositiva del 'ciclo' de quintas, cuando la música se mueve consistentemente a través de un segmento más pequeño o más grande de los recursos estructurales tonales que el círculo representa de manera abstracta." La práctica habitual es derivar la progresión del círculo de quintas de los siete tonos de la escala diatónica, más bien de la gama completa de doce tonos presentes en la escala cromática. En esta versión diatónica del círculo, una de las quintas no es una quinta verdadera: es un tritono (o una quinta disminuida), p. entre F y B en el "natural" escala diatónica (es decir, sin sostenidos ni bemoles). Así es como se deriva el círculo de quintas, a través de la permutación de la escala mayor diatónica:
Y de la escala menor (natural):
La siguiente es la secuencia básica de acordes que se pueden construir sobre la línea de bajo principal:
Y sobre el menor:
Agregar séptimas a los acordes crea una mayor sensación de impulso hacia adelante en la armonía:
época barroca
Según Richard Taruskin, Arcangelo Corelli fue el compositor más influyente en establecer el patrón como un "tropo" armónico estándar: "Fue precisamente en la época de Corelli, a finales del siglo XVII siglo, que el círculo de quintas estaba siendo 'teorizado' como el principal propulsor del movimiento armónico, y fue Corelli, más que cualquier otro compositor, quien puso en práctica esta nueva idea.
La progresión del círculo de quintas aparece con frecuencia en la música de J. S. Bach. A continuación, de Jauchzet Gott en allen Landen, BWV 51, incluso cuando la línea de bajo solista implica en lugar de afirmar los acordes involucrados:
Handel utiliza una progresión de círculo de quintas como base para el movimiento Passacaglia de su Suite para clavecín n.° 6 en sol menor.
Los compositores barrocos aprendieron a realzar la "fuerza propulsora" de la armonía engendrada por el círculo de quintas "agregando séptimas a la mayoría de los acordes constituyentes". "Estas séptimas, al ser disonancias, crean la necesidad de resolución, convirtiendo así cada progresión del círculo en un aliviador y reestimulador simultáneo de la tensión armónica... Por lo tanto, se aprovechan con fines expresivos." En el aria "Pena tiranna" en la ópera Amadigi di Gaula de Handel de 1715:
– y en el arreglo para teclado de Bach del Concierto para oboe y cuerdas de Alessandro Marcello.
Siglo XIX
Durante el siglo XIX, los compositores hicieron uso del círculo de quintas para realzar el carácter expresivo de su música. El conmovedor Impromptu en mi bemol mayor de Franz Schubert, D 899, contiene este pasaje:
– al igual que el movimiento Intermezzo del Cuarteto de Cuerdas No.2 de Mendelssohn (con el ii° sustituido por el iv):
La evocadora obra de Robert Schumann "Niño que se queda dormido" de su Kinderszenen surge una sorpresa al final de la progresión: la pieza termina en un acorde de La menor, en lugar de la tónica esperada en Mi menor.
En la ópera de Wagner, Götterdämmerung, se produce un ciclo de progresión de quintas en la música que pasa del final del prólogo a la primera escena del Acto 1, ambientada en la imponente sala. de los ricos Gibichungs. "El estatus y la reputación están escritos en todos los motivos asignados a Gunther", jefe del clan Gibichung:
Jazz y música popular
La perdurable popularidad del círculo de quintas como dispositivo de construcción de formas y como tropo musical expresivo es evidente en el número de "estándar" canciones populares compuestas durante el siglo XX. También se ve favorecido como vehículo para la improvisación de los músicos de jazz.
- Bart Howard, "Llévame a la Luna"
La canción se abre con un patrón de frases descendientes –en esencia, el gancho de la canción – presentado con una predicción calmante, casi como si la dirección futura de la melodía es dictada por la apertura de cinco notas. La progresión armónica, por su parte, raramente sale del círculo de los quintos.
- Jerome Kern, "Todas las cosas que eres"
- Ray Noble, "Cherokee". Muchos músicos de jazz han encontrado esto particularmente difícil a medida que el medio ocho progresa tan rápidamente a través del círculo, "creando una serie de progresiones II-V-I que pasan temporalmente por varias tonalidades".
- Kosmo, Prevert y Mercer, "Autumn Leaves"
- Los Beatles, "Nunca me das tu dinero"
- Mike Oldfield, "Incantaciones"
- Carlos Santana, "Europa (Sonrisa del Cielo de la Tierra)"
- Gloria Gaynor, "I will Survive"
- Pet Shop Boys, "Es un pecado"
- Donna Summer, "Amor para amarte, bebé"
Conceptos relacionados
Círculo diatónico de quintas
El círculo diatónico de quintas es el círculo de quintas que abarca solo miembros de la escala diatónica. Por tanto, contiene una quinta disminuida, en do mayor entre si y fa. Ver estructura implica multiplicidad. La progresión del círculo es comúnmente un círculo de quintas a través de los acordes diatónicos, incluido un acorde disminuido. A continuación se muestra una progresión circular en Do mayor con acordes I–IV–viio–iii–vi–ii–V–I.
- <img alt=" { new PianoStaff << new Staff <> new Staff <> >> } " height="143" src="https://upload.wikimedia.org/score/o/2/o27wiof0n2p8ap90561mhgsodeuw5ei/o27wiof0.png" width="335"/>
Círculo cromático
El círculo de quintas está estrechamente relacionado con el círculo cromático, que también organiza las doce clases de tonos de igual temperamento en un orden circular. Una diferencia clave entre los dos círculos es que el círculo cromático puede entenderse como un espacio continuo donde cada punto del círculo corresponde a una clase de tono concebible, y cada clase de tono concebible corresponde a un punto en el círculo. Por el contrario, el círculo de quintas es fundamentalmente una estructura discreta, y no existe una forma obvia de asignar clases de tono a cada uno de sus puntos. En este sentido, los dos círculos son matemáticamente bastante diferentes.
Sin embargo, las doce clases de campo iguales pueden ser representadas por el grupo cíclico de orden doce, o equivalentemente, las clases de residuos modulo doce, Z/12Z{displaystyle mathbb {Z} {Z}. El grupo Z12{displaystyle mathbb {Z} _{12} tiene cuatro generadores, que se pueden identificar con las semitonas ascendentes y descendentes y las quintas perfectas ascendentes y descendientes. El generador semitonal da lugar al círculo cromático mientras que el quinto perfecto da lugar al círculo de los quintos.
Relación con la escala cromática
El círculo de quintas, o cuartas, puede mapearse a partir de la escala cromática por multiplicación, y viceversa. Para mapear entre el círculo de quintas y la escala cromática (en notación entera) multiplicar por 7 (M7), y para el círculo de cuartas multiplicar por 5 (P5).
Aquí hay una demostración de este procedimiento. Comience con una tupla ordenada de 12 (fila de tonos) de enteros
- (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11)
que representa las notas de la escala cromática: 0 = do, 2 = re, 4 = mi, 5 = fa, 7 = sol, 9 = la, 11 = si, 1 = do♯, 3 = D♯, 6 = F♯, 8 = G♯, 10 = A♯. Ahora multiplica toda la tupla de 12 por 7:
- (0, 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77)
y luego aplique una reducción de módulo 12 a cada uno de los números (reste 12 de cada número tantas veces como sea necesario hasta que el número sea menor que 12):
- (0, 7, 2, 9, 4, 11, 6, 1, 8, 3, 10, 5)
que es equivalente a
- (C, G, D, A, E, B, F▪, C▪, G▪, D▪, A▪, F)
que es el círculo de quintas. Esto es enarmónicamente equivalente a:
- (C, G, D, A, E, B, G., D., A., E., B., F).
Equivalentes enarmónicos, tonalidades teóricas y la espiral de quintas
La afinación de temperamento igual no utiliza la proporción exacta de frecuencias de 3:2 que define una quinta perfecta, mientras que el sistema de entonación justa utiliza esta proporción exacta. Ascender por quintas en temperamento igual conduce a un regreso a la clase de tono inicial: comenzar con una C y ascender por quintas conduce a otra C después de doce iteraciones. Esto no ocurre si se usa una proporción exacta de 3:2 (solo entonación). El ajuste realizado en la afinación de temperamento igual se denomina coma pitagórica. Debido a esta diferencia, los tonos que son enarmónicamente equivalentes en la afinación de igual temperamento (por ejemplo, D♭ y C♯) no son equivalentes cuando se usa solo la entonación.
En entonación justa, la secuencia de quintas se puede visualizar como una espiral, no como un círculo: una secuencia de doce quintas da como resultado una "bomba de coma" por la coma pitagórica, visualizada como subiendo un nivel en la espiral. Ver también § Cierre de círculo en sistemas de afinación desiguales.
Sin equivalencia enarmónica, continuar una secuencia de quintas da como resultado notas con dobles alteraciones (dobles sostenidos o dobles bemoles). Cuando se usa temperamento igual, estos pueden ser reemplazados por una nota enarmónicamente equivalente.
Las claves con dos sostenidos o bemoles en las armaduras se denominan claves teóricas; su uso es extremadamente raro. La notación en estos casos no está estandarizada.
El comportamiento predeterminado de LilyPond (foto arriba) escribe afilados individuales o planos en el orden círculo-de-cinco, antes de proceder a dobles afilados o planos. Este es el formato utilizado en John Foulds A World Requiem, Op. 60, que termina con la firma clave de G▪ mayor, como se muestra arriba. Los afilados en la firma clave de G▪ de la categoría C▪, G▪, D▪, A▪, E▪, B▪, F
.
A veces se repiten afilados individuales o planos en la firma clave como cortesía, por ejemplo. Max Reger Suplemento a la Teoría de Modulación, que contiene D. minor key signatures on pp. 42–45. Estos tienen un B. al principio y también un B
al final (con un símbolo doble-flat), yendo B., E., A., D., G., C., F., B. La convención de LilyPond y Foulds suprimiría la B inicial..
A veces los dobles signos se escriben al principio de la firma clave, seguido de los signos individuales. Por ejemplo, el F. la firma clave se nota como B, E., A., D., G., C., F.. Esta convención es utilizada por Victor Ewald, por el programa Finale (software), y por algunas obras teóricas.
Contenido relacionado
La noche de un día duro (álbum)
Musical
Alambre (banda)