Circulación (física)

En física, la circulación es la integral de línea de un campo vectorial alrededor de una curva cerrada. En dinámica de fluidos, el campo es el campo de velocidad del fluido. En electrodinámica, puede ser el campo eléctrico o magnético.

La circulación fue utilizada independientemente por Frederick Lanchester, Martin Kutta y Nikolay Zhukovsky. Por lo general es denotado . (Gamma mayúscula griega).

Definición y propiedades

Si V es un campo vectorial y dl es un vector que representa la longitud diferencial de un pequeño elemento de una curva definida, la contribución de esa longitud diferencial a la circulación es dΓ:

$${displaystyle mathrm {d} Gamma =mathbf {V} cdot mathrm {d} mathbf {l} =left sometidamathbf {V} right sobre la vidaleft sometidamathrm {d} mathbf {l} right sobre la vidacos theta.}$$

Aquí, θ es el ángulo entre los vectores V y dl.

La circulación Γ de un campo vectorial V alrededor una curva cerrada C es la integral de línea:

$${displaystyle Gamma = _{C}mathbf {V} cdot mathrm {d} mathbf {l}$$

En un campo vectorial conservador, esta integral se evalúa como cero para cada curva cerrada. Eso significa que una integral de línea entre dos puntos cualesquiera en el campo es independiente del camino tomado. También implica que el campo vectorial se puede expresar como el gradiente de una función escalar, que se llama potencial.

Relación con la vorticidad y la curvatura

La circulación puede estar relacionada con la curvatura de un campo vectorial V y, más específicamente, con la vorticidad si el campo es un campo de velocidad de fluido,

$${displaystyle {boldsymbol {omega }=nabla times mathbf {V}$$

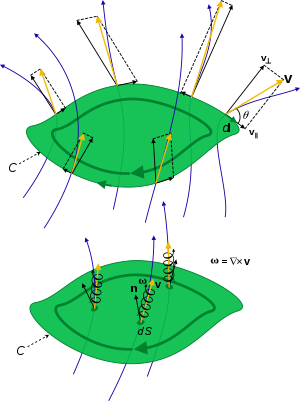
Por Stokes' teorema, el flujo de vectores de rizo o vorticidad a través de una superficie S es igual a la circulación alrededor de su perímetro,

$${displaystyle #Gamma =oint _{partial S}mathbf {V} cdot mathrm {d} mathbf {l} =iint _{S}nabla times mathbf {V} cdot mathrm {d} mathbf {S} =iint _{S}{boldsymbol {omega }cdot mathrm {d} mathbf {S}$$

Aquí, la ruta de integración cerrada ∂S es el límite o perímetro de una superficie abierta S, cuyo elemento infinitesimal normal dS = nDS está orientado según la regla de la mano derecha. Por lo tanto, el curl y la vorticidad son la circulación por área unidad, tomada alrededor de un bucle infinitesimal local.

En el flujo potencial de un fluido con una región de vorticidad, todas las curvas cerradas que encierran la vorticidad tienen el mismo valor para la circulación.

Usos

Teorema de Kutta-Joukowski en dinámica de fluidos

En la dinámica de fluidos, el elevador por unidad (L') actuando en un cuerpo en un campo de flujo bidimensional es directamente proporcional a la circulación, es decir, se puede expresar como el producto de la circulación Dimensiones sobre el cuerpo, la densidad del fluido ${displaystyle rho _{infty}$, y la velocidad del cuerpo relativa a la corriente libre ${displaystyle v_{infty}$:

$${displaystyle L'=rho _{infty }v_{infty$$

Esto se conoce como teorema de Kutta-Joukowski.

Esta ecuación se aplica a los perfiles aerodinámicos, donde la circulación se genera por la acción del perfil aerodinámico; y alrededor de objetos que giran experimentando el efecto Magnus donde la circulación se induce mecánicamente. En acción aerodinámica, la magnitud de la circulación está determinada por la condición de Kutta.

La circulación en cada curva cerrada alrededor del perfil aerodinámico tiene el mismo valor y está relacionada con la sustentación generada por cada unidad de longitud de luz. Siempre que la curva cerrada encierre el perfil aerodinámico, la elección de la curva es arbitraria.

La circulación se utiliza a menudo en dinámica de fluidos computacional como variable intermedia para calcular fuerzas sobre un perfil aerodinámico u otro cuerpo.

Ecuaciones fundamentales del electromagnetismo

En electrodinámica, la ley de inducción de Maxwell-Faraday se puede expresar de dos formas equivalentes: que la curvatura del campo eléctrico es igual a la tasa de cambio negativa del campo magnético,

$${displaystyle nabla times mathbf {E} =-{frac {partial mathbf {B}{partial t}}$$

o que la circulación del campo eléctrico alrededor de una espira es igual a la tasa de cambio negativa del flujo del campo magnético a través de cualquier superficie atravesada por la espira, según Stokes' teorema

$${displaystyle oint _{partial S'mathbf {E} cdot mathrm {d} mathbf {l} =iint _{S}nabla times mathbf {E} cdot mathrm {d} mathbf {S} =-{frac {mathrm {d} }{mathrm {d}. ¿Qué? {B} cdot mathrm {d} mathbf {S}$$

La circulación de un campo magnético estático es, según la ley de Ampère, proporcional a la corriente total encerrada por el bucle

$${displaystyle oint _{partial S'mathbf {B} cdot mathrm {d} mathbf {l} =mu _{0}iint {}cdot mathrm {d} mathbf {S} =mu} Yo...$$

Para sistemas con campos eléctricos que cambian con el tiempo, la ley debe modificarse para incluir un término conocido como corrección de Maxwell.