Circuito LC

Un circuito LC, también llamado circuito resonante, circuito tanque o circuito sintonizado, es un Circuito eléctrico formado por un inductor, representado por la letra L, y un condensador, representado por la letra C, conectados entre sí. El circuito puede actuar como un resonador eléctrico, un análogo eléctrico de un diapasón, almacenando energía que oscila a la frecuencia de resonancia del circuito.

• 

  diagrama de circuito LC

• 

  Circuito LC (izquierda) consistente en bobina ferrite y condensador usado como un circuito sintonizado en el receptor para un reloj de radio

• 

  Salida circuito sintonizado de radio transmisor de onda corta

Los circuitos LC se utilizan para generar señales a una frecuencia particular o para seleccionar una señal a una frecuencia particular a partir de una señal más compleja; esta función se llama filtro de paso de banda. Son componentes clave en muchos dispositivos electrónicos, particularmente equipos de radio, utilizados en circuitos como osciladores, filtros, sintonizadores y mezcladores de frecuencia.

Un circuito LC es un modelo idealizado ya que supone que no hay disipación de energía debido a la resistencia. Cualquier implementación práctica de un circuito LC siempre incluirá pérdidas resultantes de una resistencia pequeña pero distinta de cero dentro de los componentes y cables de conexión. El propósito de un circuito LC suele ser oscilar con una amortiguación mínima, por lo que la resistencia es lo más baja posible. Si bien ningún circuito práctico está libre de pérdidas, es instructivo estudiar esta forma ideal del circuito para ganar comprensión e intuición física. Para ver un modelo de circuito que incorpora resistencia, consulte Circuito RLC.

Terminología

El circuito LC de dos elementos descrito anteriormente es el tipo más simple de red inductor-condensador (o red LC). También se le conoce como circuito LC de segundo orden para distinguirlo de redes LC más complicadas (de orden superior) con más inductores y condensadores. Estas redes LC con más de dos reactancias pueden tener más de una frecuencia de resonancia.

El orden de la red es el orden de la función racional que describe la red en la variable de frecuencia compleja s. Generalmente el orden es igual al número de elementos L y C del circuito y en ningún caso puede exceder este número.

Operación

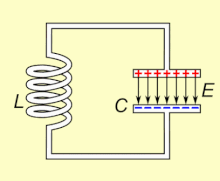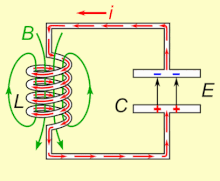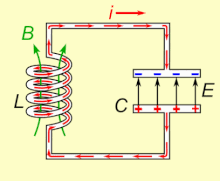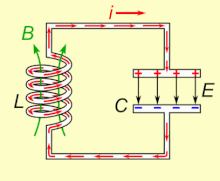
Un circuito LC, que oscila a su frecuencia de resonancia natural, puede almacenar energía eléctrica. Ver la animación. Un condensador almacena energía en el campo eléctrico (E) entre sus placas, dependiendo del voltaje que lo atraviesa, y un inductor almacena energía en su campo magnético (B), dependiendo de la corriente que lo atraviesa.

Si se conecta un inductor a través de un capacitor cargado, el voltaje a través del capacitor impulsará una corriente a través del inductor, generando un campo magnético a su alrededor. El voltaje a través del capacitor cae a cero a medida que el flujo de corriente consume la carga. En este punto, la energía almacenada en el campo magnético de la bobina induce un voltaje a través de la bobina, porque los inductores se oponen a los cambios en la corriente. Este voltaje inducido hace que una corriente comience a recargar el capacitor con un voltaje de polaridad opuesta a su carga original. Debido a la ley de Faraday, la FEM que impulsa la corriente es causada por una disminución en el campo magnético, por lo que la energía requerida para cargar el capacitor se extrae del campo magnético. Cuando el campo magnético se disipe por completo, la corriente se detendrá y la carga volverá a almacenarse en el condensador, con la polaridad opuesta a la anterior. Entonces el ciclo comenzará de nuevo, con la corriente fluyendo en dirección opuesta a través del inductor.

La carga fluye de ida y vuelta entre las placas del condensador, a través del ductor. La energía oscila de ida y vuelta entre el condensador y el ductor hasta que (si no se repone de un circuito externo) la resistencia interna hace que las oscilaciones mueran. La acción del circuito sintonizado, conocida matemáticamente como un oscilador armónico, es similar a un péndulo oscilando de ida y vuelta, o el agua que de ida y vuelta en un tanque; por esta razón el circuito también se llama un circuito de tanques. La frecuencia natural (es decir, la frecuencia en la que oscilará cuando está aislada de cualquier otro sistema, como se describe anteriormente) se determina por los valores de capacitancia e inductancia. En la mayoría de las aplicaciones el circuito sintonizado es parte de un circuito más grande que aplica corriente alterna a él, conduciendo oscilaciones continuas. Si la frecuencia de la corriente aplicada es la frecuencia resonante natural del circuito (frecuencia natural) ${displaystyle f_{0},}$ abajo), la resonancia ocurrirá, y una pequeña corriente de conducción puede excitar grandes amplitudes oscilando voltajes y corrientes. En los típicos circuitos sintonizados en el equipo electrónico las oscilaciones son muy rápidas, de miles a miles de millones de veces por segundo.

Efecto de resonancia

La resonancia se produce cuando un circuito LC es accionado desde una fuente externa a una frecuencia angular ω₀ a la que el Las reactancias inductiva y capacitiva son iguales en magnitud. La frecuencia a la que se cumple esta igualdad para un circuito particular se llama frecuencia de resonancia. La frecuencia de resonancia del circuito LC es

${displaystyle omega ¿Qué?$

donde L es la inductancia en henrios y C es la capacitancia en faradios. La frecuencia angular ω₀ tiene unidades de radianes por segundo.

La frecuencia equivalente en unidades de hercios es

${displaystyle F_{0}={frac {omega _{0}{2pi {fnMicroc}{2pi} {cHFF}.$

Aplicaciones

El efecto de resonancia del circuito LC tiene muchas aplicaciones importantes en sistemas de comunicaciones y procesamiento de señales.

• La aplicación más común de los circuitos de tanques es tuning transmisores de radio y receptores. Por ejemplo, al ajustar una radio a una estación en particular, los circuitos LC se fijan en resonancia para esa frecuencia de transporte particular.
• Un circuito de resonancia de serie proporciona aumento de tensión.
• Un circuito resonante paralelo proporciona aumento actual.
• Un circuito resonante paralelo se puede utilizar como impedancia de carga en circuitos de salida de amplificadores RF. Debido a la alta impedancia, la ganancia de amplificador es máxima a la frecuencia resonante.
• Tanto los circuitos resonantes paralelos como las series se utilizan en calefacción de inducción.

Los circuitos LC se comportan como resonadores electrónicos, que son un componente clave en muchas aplicaciones:

• Amplificadores
• Osciladores
• Filtros
• Tuners
• Mixers
• Foster-Seeley discriminador
• Tarjetas sin contacto
• Tabletas gráficas
• Vigilancia electrónica de artículos (marcas de seguridad)

Solución en el dominio del tiempo

Las leyes de Kirchhoff

Según la ley de voltaje de Kirchhoff, el voltaje V_C a través del capacitor más el voltaje V_L a través del inductor debe ser igual a cero:

${displaystyle V_{C}+V_{L}=0.}$

Del mismo modo, según la ley de corrientes de Kirchhoff, la corriente que pasa por el condensador es igual a la corriente que pasa por el inductor:

${displaystyle I_{C}=I_{L}$

A partir de las relaciones constitutivas de los elementos del circuito, también sabemos que

${displaystyle {begin{aligned}V_{L}(t) Yo... {mhm} ¿Qué?$

Ecuación diferencial

Reorganizar y sustituir da la ecuación diferencial de segundo orden

${displaystyle {frac {mathrm}{2}{2}{mathrm {d} t^{2}}I(t)+{frac {1}{LC}I(t)=0}$

El parámetro ω₀, la frecuencia angular resonante, se define como

${displaystyle omega ¿Qué? {C}}}$

Usar esto puede simplificar la ecuación diferencial:

${displaystyle {frac {mathrm}{2}{2}{mathrm {d} t^{2}}I(t)+omega _{0}{2}I(t)=0.}$

La transformación de Laplace asociada es

${displaystyle s^{2}+omega ¿Qué?$

así

${displaystyle s=pm jomega _{0}$

donde j es la unidad imaginaria.

Solución

Por lo tanto, la solución completa de la ecuación diferencial es

${displaystyle I(t)=Ae^{+jomega ¿Qué? - No.$

y se puede resolver para A y B considerando las condiciones iniciales. Como la exponencial es compleja, la solución representa una corriente alterna sinusoidal. Dado que la corriente eléctrica I es una cantidad física, debe tener un valor real. Como resultado, se puede demostrar que las constantes A y B deben ser conjugados complejos:

${displaystyle A=B^{*}$

Ahora deja que

${displaystyle A={frac {I_{0} {2}e^{+jphi }}$

Por lo tanto,

${displaystyle B={frac {I_{0} {2}e^{-jphi }$

A continuación, podemos usar la fórmula de Euler para obtener un verdadero sinusoide con amplitud I₀, frecuencia angular ⋅₀ = 1/√LC, y ángulo de fase ${displaystyle phi }$.

Así, la solución resultante se convierte en

${displaystyle I(t)=I_{0}cos left(omega _{0}t+phi right),}$

${displaystyle V_{L}(t)=L{frac {mathrm {d} I'{mathrm {d}=-omega _{0}li_{0}sin left(omega _{0}t+phi right). }$

Condiciones iniciales

Las condiciones iniciales que satisfacerían este resultado son

${displaystyle I(0)=I_{0}cos phi}$

${displaystyle V_{L}(0)=L{frac {mathrm {d} Yo... Silencio. ¿Por qué?$

Circuito en serie

En la configuración en serie del circuito LC, el inductor (L) y el condensador (C) están conectados en serie, como se muestra aquí. El voltaje total V a través de los terminales abiertos es simplemente la suma del voltaje a través del inductor y el voltaje a través del capacitor. La corriente I en el terminal positivo del circuito es igual a la corriente que pasa por el capacitor y el inductor.

${displaystyle {begin{aligned}V=V_{L}+V_{C},\I simultáneamente=I_{L}=I_{C}end{aligned}}}$

Resonancia

Reacción inductiva ${displaystyle X_{mathsf {L}=omega L.$ aumenta a medida que aumenta la frecuencia, mientras que la reacción capacitiva ${displaystyle X_{mathsf {C}={frac} {1}{\\fn}}}$ disminuciones con aumento de frecuencia (definido aquí como un número positivo). A una frecuencia particular, estas dos reacciones son iguales y los voltajes a través de ellas son iguales y opuestos en señal; esa frecuencia se llama frecuencia resonante f₀ para el circuito dado.

Por lo tanto, en resonancia,

${displaystyle {begin{aligned}X_{mathsf {L}=X_{mathsf {C}\\\fnMiega Liéndose={frac} {1}{\\fnMiega - ¿Qué?$

Resolviendo para ω, tenemos

${displaystyle omega =omega ¿Qué? {sqrt {LC;}} }$

que se define como la frecuencia angular resonante del circuito. Al convertir la frecuencia angular (en radianes por segundo) en frecuencia (en Hertz), se tiene

${displaystyle F_{0}={frac {omega ¿Por qué? 2 'pi {sqrt {LC;} }$

y

${displaystyle X_{Mathsf {}0}=X_{mathsf {C}0}={sqrt {frac {f} {f}}}}}}}}}}$

a ${displaystyle omega ¿Qué?$.

En una configuración en serie, X_C y X_L se cancelan entre sí. En los componentes reales, más que en los idealizados, la corriente se opone, principalmente por la resistencia de los devanados de la bobina. Por tanto, la corriente suministrada a un circuito resonante en serie es máxima en resonancia.

• En el límite como f → f₀ la corriente es máxima. La impedancia del circuito es mínima. En este estado, un circuito se llama un circuito de aceptadores
• Para f.f₀, X_L ≪ X_C; por lo tanto, el circuito es capacitivo.
• Para f■f₀, X_L ≫ X_C; por lo tanto, el circuito es inductivo.

Impedancia

En la configuración de la serie, la resonancia ocurre cuando la impedancia eléctrica compleja del circuito se acerca a cero.

Primero considere la impedancia del circuito de la serie LC. La impedancia total viene dada por la suma de las impedancias inductivas y capacitivas:

${displaystyle Z=Z_{mathsf {L}+Z_{mathsf {C}~}$

Escribir la impedancia inductiva como Z_L = < i>jωL e impedancia capacitiva como Z_C = 1/j ω C y sustituyendo da

${displaystyle Z(omega)=jomega L+{frac {1}{ jomega - Sí.$

Escribir esta expresión bajo un denominador común da

${displaystyle Z(omega)=jleft({frac {\omega ^{2}LC-1 }{omega C}}right)~.}$

Finalmente, definir la frecuencia angular natural como

${displaystyle omega ¿Qué? {sqrt {LC;}} }$

la impedancia se convierte

${displaystyle Z(omega)=j Lleft({frac {omega ^{2}-omega _{0}{2} }{omega }}right)=jomega _{0}Lleft(frac {omega) }{\omega ¿Qué? }-{frac {\omega {fnK} {fnK}}derecha)=j {frac {1}{\mega ¿Por qué? ¿Qué? }-{frac {omega _{0}{omega }right)}$

Donde ${displaystyle ,omega _{0}L ,}$ da la reacción del ductor a la resonancia.

El numerador implica que en el límite como ⋅ → ±⋅₀, la impedancia total Z será cero y no cero. Por lo tanto, el circuito LC serie, cuando se conecta en serie con una carga, actuará como un filtro de paso de banda con impedancia cero en la frecuencia resonante del circuito LC.

Circuito paralelo

Cuando el inductor (L) y el condensador (C) están conectados en paralelo como se muestra aquí, el voltaje V a través del terminales abiertos es igual al voltaje a través del inductor y al voltaje a través del capacitor. La corriente total I que fluye hacia el terminal positivo del circuito es igual a la suma de la corriente que fluye a través del inductor y la corriente que fluye a través del condensador:

${displaystyle {begin{aligned}V=V_{mathsf {L}=V_{mathsf {C}\\\fnMicrosoft Sans {L}+I_{mathsf {C}~.end{aligned}}$

Resonancia

Cuando X_L es igual a X_C, las dos corrientes de rama son iguales y opuestas. Se cancelan entre sí para dar una corriente mínima en la línea principal (en principio, corriente cero). Sin embargo, hay una gran corriente circulando entre el condensador y el inductor. En principio, esta corriente circulante es infinita, pero en realidad está limitada por la resistencia del circuito, particularmente la resistencia en los devanados del inductor. Como la corriente total es mínima, en este estado la impedancia total es máxima.

La frecuencia de resonancia está dada por

${displaystyle F_{0}={frac {omega ¿Por qué? 2pi {sqrt {LC;}} }~$

Cualquier corriente de rama no es mínima a la resonancia, pero cada se da por separado por el voltaje de fuente divisoria (V) por reacción (Z). Por lo tantoI = V/ZDe acuerdo con la ley de Ohm.

• Atf₀, la corriente de línea es mínima. La impedancia total es máxima. En este estado se llama un circuito circuito de rechazo.
• A continuaciónf₀El circuito es inductivo.
• Arribaf₀, el circuito es capacitivo.

Impedancia

El mismo análisis se puede aplicar al circuito LC paralelo. La impedancia total entonces viene dada por

${displaystyle Z={frac {fnMicrosoft Sans Serif} {C} }{Z_{mathsf {L}+Z_{mathsf {C}} '$

y después de la sustitución de z _l = J ω l y z _c = 1 / j ω c y simplificación, da

${displaystyle Z(omega)=-jcdot {frac {omega L} {fnMiega }}~$

Usando

${displaystyle omega ¿Qué? {sqrt {LC;}} }$

se simplifica aún más

${displaystyle Z(omega)=-jleft({frac {1}{fn}derecha)left({frac {omega }{\omega ¿Qué? omega Cleft({tfrac {omega) ## {0}{omega ¿Qué? }=+j {frac {omega _{0}L}{left({tfrac {omega ## {0}{omega ¿Qué? }~$

Note que

${displaystyle lim _{omega to omega ¿Qué?$

pero para todos los demás valores de ω la impedancia es finita.

Por lo tanto, el circuito LC paralelo conectado en serie con una carga actuará como filtro de eliminación de banda que tiene una impedancia infinita en la frecuencia de resonancia del circuito LC, mientras que el circuito LC paralelo conectado en paralelo con una carga actuará como filtro de banda. pasar el filtro.

Solución de Laplace

El circuito LC se puede resolver utilizando la transformada de Laplace.

Comenzamos definiendo la relación entre corriente y voltaje a través del capacitor y el inductor de la manera habitual:

${displaystyle v_{mathrm}(t)=v(t)~}$ ${displaystyle i(t)=C {fnK} v_{mathrm {C} {fn} {fnMicrosoft}} {fnMicrosoft}} {fnMicrosoft}} {fn}}} {fn}}}} {fnK}}}} {fnK}}}}}} {\fnK}}}}}} {fnK}}}}}}}}}} {m}}}}}} {m}}}}}} {m} {m}}}} {m}}}}} {m}}}}} {m} {m}} {m} {m}}}}}}}}}}}}}}}}}}}}}} {m}} {m} {m}}} {m}}}}} {m}} {m}m}} {m}}}} {m}} {m}}}}}}}}}}}}}}}}}}}} {m}}}.$ y ${displaystyle ~v_{mathrm {L}(t)=L {frac {mathrm {d}{mathrm {d}} {} {} {}} {fn} {fnK}} {fn}} {}} {f}} {f}}}} {fnKf}f}}}}f}}}f}}}}}f}f}}}f}f}f}fnKfnKfnKfnKfnKfnKfnKfnKfnKfnKfnKfnKfnKfnKfnKfnKfnKfnKfnKfnKfnKfnKfnKfnKfnKfnKfnKfnKfnKfnK}}}}}}}}}}.$

Luego mediante la aplicación de las leyes de Kirchoff, podemos llegar a las ecuaciones diferenciales del sistema

${displaystyle v_{in}(t)=v_{mathrm {L}(t)+v_{mathrm {C}(t)=Lfrac {mathrm {d} {i}{mathrm {d} {d} {} {} {}} {} {}}}} {f}} {f}} {f}}}}} {f}}}}}}}}}}} {f}}}}}}}} {f} {f} {f}}}}} {f}}}}} {f}}}} {f}}}}}}}} {f}}}}}}} {f}}}}}}} {f}}} {f}}}}}}}}}}}}}}}}} {f}}}} {f}}}}}}}}}}}}}}}}} {f}}}}}}}}}}}} t}+v=L C {fnMicroc {fnK}+v;$

Con condiciones iniciales ${displaystyle v(0)=v_{0} }$ y ${displaystyle i(0)=i_{0}=Ccdot v'(0)=Ccdot - ¿Qué?$

Haciendo las siguientes definiciones,

${displaystyle omega ################################################################################################################################################################################################################################################################ ♪♪$ y ${displaystyle ~f(t)equiv omega _{0}{2} v_{mathrm {in}(t)}$

da

${displaystyle f(t)={frac {m} {c} {c}cc}{m} {d} T^{2}}+omega ¿Qué?$

Ahora aplicamos la transformada de Laplace.

${fnK} left[ f(t)right]=operatorname {mathcal {L}left[ {\\fnhm {d} } } } {m}m} {fn} {}m} {} {} {f}}} {f}f}f}f}f}f}f}f}f} {f}f}f}f}f}f}f} {f}f}f}}f}f}f}}f}f}f}f}f}f}f}f}f}f}f}f}f}}}}f}f}f}f}f}f}f}}f}f}}f}f}f}f}f}f}f}f}}f}f} T^{2}}+omega ¿Qué?$

${displaystyle F(s)=s^{2} V(s)-s v_{0}-v'_{0}+omega ¿Qué? V(s);.}$

El Laplace transforma ha convertido nuestra ecuación diferencial en una ecuación algebraica. Solving for V en el s dominio (dominio de frecuencia) es mucho más simple.

${displaystyle V(s)={frac { s v_{0}+v'_{0}+F(s) ¿Qué?$

${displaystyle V(s)={frac { s {0}{2}+omega - ¿Qué? {cH00} {cH00} {cH00}} {cH00}} {cH00}} {cH00}}}m}}mega ¿Qué? }{2}+omega ¿Qué?$

Que se puede transformar nuevamente al dominio del tiempo mediante la transformada inversa de Laplace:

${displaystyle v(t)=operatorname {mathcal {L} ^{-1}left[ V(s)right]}$

${displaystyle v(t)=fnMitcal {fnMitcal {fnh} {fnMicroc {c scH00} {0}{2}+omega - ¿Qué? {cH00} {cH00}} {cH00} {cH00}} {cH00}} {cH00}}}m}}mega ¿Qué? }{2}+omega ¿Qué?$

Para la segunda suma, una fracción equivalente ${displaystyle omega ¿Qué?$ es necesario:

${displaystyle v(t)=v_{0}operatorname {fnMitcal {fnMicrosoft}cHFF} {fnMitcal {fnh} {fnK}}b}cH00}cH00}cHFF}cHFF} {fnMicroc {cHFF} {cHFF}fnK} ¿Por qué? {0}{0}{0} {0} {0}}}}}} right]+operatorname {mathcal {L} ^{-1}left[ {frac {F(s) }{2}+omega ¿Qué?$

Para la segunda suma, una fracción equivalente ${displaystyle omega ¿Qué?$ es necesario:

${displaystyle v(t)=v_{0}operatorname {fnMitcal {fnMicrosoft}cHFF} {fnMitcal {fnh} {fnK}}b}cH00}cH00}cHFF}cHFF} {fnMicroc {cHFF} {cHFF}fnK} ¿Qué? right]+{frac {fnMiega} ¿Qué? #frac {omega ¿Por qué? right]+operatorname {mathcal {L} ^{-1}left[ {frac {F(s) }{2}+omega ¿Qué?$

${displaystyle v(t)=v_{0}cos(omega _{0} t)+{frac {v'_{0}}{omega _{0}\\\fnMiega _{0} t)+operatorname {mathcal {L}} ^{-1}left[ {fnMicroc {F(s)}{\fnMitcal {f}}fnKfnMicroc} {f}}}}}{f}f}}f}f}}f}fnKf}f}f}f}f}f}f}fnKf}fnKfnfnKf}fnKf}fnKfnKfnKfnKfnKfnun}fnKfnKfnKfnKfnKfnKfnKfnKfnKfnKfnKf}fnKfnKfn - ¿Qué?$

El término final depende de la forma exacta del voltaje de entrada. Dos casos comunes son la función escalonada de Heaviside y una onda sinusoidal. Para una función de paso de Heaviside obtenemos

${displaystyle v_{mathrm {in}(t)=M u(t),}$

${displaystyle operatorname {mathcal {L} ^{-1}left[\omega ¿Qué? s^{2}+omega ¿Qué? ###### ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ## ### ## ## ## ## ## ## ##### ## ## ## #### M {frac {1}{2}+omega _{0}} {fnMicrosoft Sans Serif}$

${displaystyle v(t)=v_{0}cos(omega _{0} t)+{frac {fnK} {fnMiega} ##########################Bigl (}1-cos(omega _{0} t){Bigr)};.}$

Para el caso de una función sinusoidal como entrada obtenemos:

${displaystyle v_{mathrm {in}(t)=Usin(omega _{mathrm {f} t) Rightarrow V_{mathrm {in}(s)={frac {frac} U omega _{mathrm {f} } { s^{2}+omega _{mathrm {f} {2} }\,}$

Donde ${displaystyle U}$ es la amplitud y ${displaystyle omega _{f}$ la frecuencia de la función aplicada.

${displaystyle operatorname {mathcal {L} ^{-1}left[omega _{0}{2} {frac {1}{f}{f} {f} {f}f}\fn}\f}\fnK}f}\fnKf}f}\f}\fnKfnK}\fnK}}\\fnKfnK\\fnK}fnK}\\fnK}\\\\\fnK}}\\fnK}fnK\\\fnKfnK}fnK}\fnK}fnK}\fnK}}\fnK}fnK}fnK}\\\fnK}}\\\\\fnK s^{2}+omega ¿Qué? {frac {\fnMiga* _{mathrm} } { s^{2}+omega _{mathrm {f} {2}\\s}\s}}$

Utilizando el método de fracción parcial:

${displaystyle operatorname {mathcal {L} ^{-1}left[omega _{0}{2} U omega _{mathrm {f}{frac {1}{ s^{2}+omega ¿Qué? {fnK} {fnMicroc} {fnMicroc} {fnMicroc} {fnMicroc} {f} {fn} {fnMicroc} {fnMicroc} {fnMicroc} {fnMicroc} {f} {fnMicroc}} {f}} {f} {f}}} {f}}{f} {\f}}f}\f}f}f} {f}f}} {f}fn\fnfnfnfnf}fnfnfnfnfnfnfn\fnMicrocfnfn\fnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfn s^{2}+omega _{mathrm {f}} {2}\\right]=operatorname {mathcal {L} } ^{-1}left[omega _{0}2} U omega _{mathrm {f}{frac {A+Bs}{2}+omega ¿Qué? {fnMicroc {C+Ds}{2}+omega _{mathrm {f}} {2}}\derecha]}$

Simplificando por ambos lados

${displaystyle 1=(A+Bs)( s^{2}+omega _{mathrm {f}^{2})+(C+Ds)( s^{2}+omega _{0}^{2})})}$

${displaystyle 1=(A s^{2}+ A omega _{mathrm {f}{2} + B s^{3}+ B omega _{mathrm {f} {2})+ C s^{2}+ C omega _{0}{2} + D s^{3}+ D somega _{0} {2})}$

${displaystyle 1=s^{3}(B + D)+s^{2}(A + C)+s(B omega _{mathrm {f}}{2}+ Domega _{0}{2})+(A\omega _{mathrm {f} }^{2} + C\omega _{0}{2}$

Resolvemos la ecuación para A, B y C:

${displaystyle A+C=0Rightarrow C=-A.$

${displaystyle A omega _{mathrm {f}{2} + C omega ¿Qué? Derecho A omega _{mathrm {f}{2} A omega ¿Qué?$

${displaystyle Rightarrow A ={frac {1}{omega _{mathrm {f}^{2} ################################################################################################################################################################################################################################################################$

${displaystyle Rightarrow C =-{frac {1}{2}mega _{m}} {2}cH00} ################################################################################################################################################################################################################################################################$

${displaystyle B+C=0$

${displaystyle Bomega _{mathrm {f}{2}+ D\omega ¿Qué? Derecho Bomega _{mathrm {f}{2}- B\omega ¿Qué? Derecho B (omega _{mathrm} {2}-omega ¿Qué?$

${displaystyle Rightarrow B=0, D=0}$

Sustituir los valores de A, B y C:

${displaystyle operatorname {mathcal {L} ^{-1}left[omega _{0}{2} U\omega _{mathrm {f}{frac {frac {1}{2}mega _{m}} {2}cH00} ################################################################################################################################################################################################################################################################ s^{2}+omega ¿Qué? ¿Qué? ################################################################################################################################################################################################################################################################ - ¿Qué?$

Aislar la constante y usar fracciones equivalentes para ajustar la falta de numerador:

${displaystyle {frac {\fn\fn\fn\fn\fn\\c\\\c\\\c\\\c\\\\\\c\\\\c\c\c\\\\\\\c\\\c\\c\\\c\\\ccc\\\cc\\\\\\c\\\\\\c\\\\\\\c\\\c\\\c\\c\\\c\\\\\c\\\\\\cc\\\c\ ¿Qué? Uomega omega _{mathrm {f} }{2}-omega ¿Qué? {fnK} {fnK}m}cH00}fnh}fn}m}ccH00}cc}c}ccH}c}c}c}cc}cc}c}c}c}cH}c}c}c}cH}cH}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}c}cH}c}c}c}c}c}c}c}c}c}cH {0}{0}{0}{0}omega ¿Por qué? ¿Por qué?$

Realizando la transformada inversa de Laplace en cada sumandos:

${displaystyle {frac {\fn\fn\fn\fn\fn\\c\\\c\\\c\\\c\\\\\\c\\\\c\c\c\\\\\\\c\\\c\\c\\\c\\\ccc\\\cc\\\\\\c\\\\\\c\\\\\\\c\\\c\\\c\\c\\\c\\\\\c\\\\\\cc\\\c\ ¿Qué? Uomega omega _{mathrm {f} }{2}-omega - ¿Qué? {fnMitcal {fnMicrosoft}cHFF} {fnMitcal {fnh} {fnK}}b}cH00}cH00}cHFF}cHFF} {fnMicroc {1}{omega {fnK} {fnMiega} {0}{2}+omega ¿Qué? {fnMitcal {fnMicroc} {1}{omega _{mathrm {f} {f} {f} {f} {f} {f}f} {f}f}mega _{f}}}}}derecha]derecha), }$

${displaystyle {frac {\\fn\fn\fn\\fn\\fn\\\\\fn\\c\\\\\\c\\\\\\c\\\c\\\\\\\c\\\\\c\\\c\\\ccc\\\\c\\c\\\\\\\\\\c\\\\\\\\\\\c\\ccc\\\\\c\\\\\c\\\\\\c\\\c\ ¿Qué? Uomega omega _{mathrm {f} }{2}-omega ¿Qué? {1}{omega - ¿Qué? {fnMicroc} {fnK}fnh}fnhfnh}fnh}fnh} {0}{2}+omega Está bien. {1}{omega _{mathrm {f}}\f}f}operatorname {mathcal {} } ^{-1}left[{frac {omega _{mathrm {f}} { }{2}+omega _{f}}}}}}}derecha]derecha) }$

${displaystyle v_{mathrm}(t)={frac {fnMiega _{0}{2} U omega _{mathrm {f} ##{omega _{mathrm {f} }{2}-omega {f} {f}f}fnK}f}\f}\f}\f}\f}mega _{0} t)-{frac {1}{omega _{m}f}\s}sin(omega _{m} {f}f}f}f}f}f}f}}f}f}f}f}f}m}f}f}f}f}f}f}f}\\f}f}cH0}f}f}f}f}f}f}f}f}f}f}f}f}\\cH00}f}cH00}f}\\\cH00}cH0}cH00}\cH0}cH0}cH00}\cH00} }$

Usando condiciones iniciales en la solución de Laplace:

${displaystyle v(t)=v_{0}cos(omega _{0} t)+{frac {fnK} {fnMiega} ¿Por qué? ¿Qué? U omega _{mathrm {f}{\ omega _{mathrm {f} }{2}-omega {fnMiega _{0}f}m}\fnMiga _\m}\mn\cH0}\mega _{0} t)-{frac {1}{mega _{m}\f}\s\m}\m2fnMiega _{m}f}}f}}}f}}\\f}f}f}f}f}f}f}f}f}f}f}f}f}f}\\\\f}f}f}\\\f}f}f}\f}f}f}f}f}f}f}f}\\f}f}f}fnMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMinMi$

Historia

La primera evidencia de que un capacitor y un inductor podían producir oscilaciones eléctricas fue descubierta en 1826 por el científico francés Felix Savary. Descubrió que cuando se descargaba una jarra de Leyden a través de un alambre enrollado alrededor de una aguja de hierro, a veces la aguja quedaba magnetizada en una dirección y otras en la dirección opuesta. Dedujo correctamente que esto era causado por una corriente de descarga oscilante amortiguada en el cable, que invertía la magnetización de la aguja hacia adelante y hacia atrás hasta que era demasiado pequeña para tener efecto, dejando la aguja magnetizada en una dirección aleatoria. El físico estadounidense Joseph Henry repitió el experimento de Savary en 1842 y llegó a la misma conclusión, aparentemente de forma independiente.

El científico irlandés William Thomson (Lord Kelvin) demostró matemáticamente en 1853 que la descarga de una jarra de Leyden a través de una inductancia debería ser oscilatoria, y derivó su frecuencia de resonancia. El investigador de radio británico Oliver Lodge, al descargar una gran batería de frascos de Leyden a través de un cable largo, creó un circuito sintonizado con su frecuencia resonante en el rango de audio, que producía un tono musical a partir de la chispa cuando se descargaba. En 1857, el físico alemán Berend Wilhelm Feddersen fotografió la chispa producida por un circuito resonante de jarra de Leyden en un espejo giratorio, proporcionando evidencia visible de las oscilaciones. En 1868, el físico escocés James Clerk Maxwell calculó el efecto de aplicar una corriente alterna a un circuito con inductancia y capacitancia, demostrando que la respuesta es máxima en la frecuencia de resonancia. El primer ejemplo de una curva de resonancia eléctrica fue publicado en 1887 por el físico alemán Heinrich Hertz en su artículo pionero sobre el descubrimiento de las ondas de radio, mostrando la longitud de la chispa que se puede obtener de sus detectores resonadores LC de chispa en función de la frecuencia.

Una de las primeras demostraciones de resonancia entre circuitos sintonizados fueron los "frascos sintónicos" experimento alrededor de 1889. Colocó dos circuitos resonantes uno al lado del otro, cada uno de los cuales consistía en una jarra de Leyden conectada a una bobina ajustable de una vuelta con un descargador de chispas. Cuando se aplicó un alto voltaje de una bobina de inducción a un circuito sintonizado, creando chispas y, por tanto, corrientes oscilantes, se excitaron chispas en el otro circuito sintonizado sólo cuando los circuitos se ajustaron a la resonancia. Lodge y algunos científicos ingleses prefirieron el término "síntonía" para este efecto, pero el término "resonancia" finalmente estancado. El primer uso práctico de los circuitos LC fue en la década de 1890 en transmisores de radio de chispa para permitir que el receptor y el transmisor se sintonizaran en la misma frecuencia. Lodge presentó la primera patente para un sistema de radio que permitía la sintonización en 1897, aunque los primeros sistemas prácticos fueron inventados en 1900 por el pionero de la radio italiana Guglielmo Marconi.